特大悬索桥现场隧道锚塞体的自平衡法承载特性研究

戴自然，廖万辉，周 旭，吴福飞，杨冬升

(1.贵州师范大学 材料与建筑工程学院，贵州 贵阳 550025； 2.贵州省公路工程集团有限公司，贵州 贵阳 550001)

0 引言

悬索桥[1-4]整体造型美观流畅，相比其他桥梁具有加固、维护和改建便利以及施工快捷的特点。锚塞体作为悬索桥的4大部件之一[5-7]，在实际工程中，与围岩一起均要承受桥梁静载、行车动载和风荷载等其他不可遇见荷载的作用。因此，锚塞体和围岩在荷载作用下的安全性是悬索桥的关键问题之一[8-10]。

为了验证锚塞体和围岩在荷载作用下的安全性，国内学者张奇华采用现场和数值模拟发现，围岩破坏面主要发生在围岩接触面和锚体底部，扩散向外呈圆台桩发展[11]。李栋梁采用1∶10的原位模型试验，分析了围岩的变形和长期稳定性，并提出了浅埋软岩隧道锚的破坏形式[12]。童俊采用1∶10模型试验结合有限元分析，试验发现荷载达到8倍设计荷载时锚塞体发生破坏[13]。王东英采用Mindlin应力解，提出了隧道锚极限承载力的计算公式，通过实际工程，与室内试验验证其合理性[14]。王中豪基于隧道锚承载能力计算公式缺乏的问题，提出了承载能力非线性映射PSO-LSSVM模型，通过试验证明了PSO-LSSVM模型预测结果的合理性[15]。

自平衡法[16]是近些年来新发展的测桩承载力的方法，由于不需外部加载反力，以自身承载能力作为加载的反力，实现自我加载，可以在面临超大吨、边坡、水上等试验环境困难时，完成堆载法、锚桩法等传统加载方法难以完成的试验。然而用于隧道锚塞体的试验检测还不多见。为此，本研究借助自平衡测试方法，以开州湖大桥隧道锚塞体为例，采用现场模型试验验证现场隧道锚塞体自平衡的承载特性，为类似桥梁工程的长期安全性评价提供参考。

1 工程概况与地质构造

1.1 工程概况

开州湖特大桥位于贵州黔北山地，地势总体西北高东南低，属浅切低山溶蚀、侵蚀地貌类型。桥长1 257 m，上部结构：3×30 m T梁+(1 100) m悬索桥+2×30 m T梁，孔跨布置：主桥为单跨1 100 m钢桁梁悬索桥；两岸主缆边跨分别为302,143 m，主缆垂跨比1/10，主塔塔高分别为139，141 m，引桥为预应力混凝土T梁桥。下部结构：主塔采用薄壁空心钢筋混凝土桥塔，承台群桩基础；引桥墩为双柱式圆墩，圆桩基础；锚碇为重力式(瓮安岸)及隧道式锚(开阳岸)。开阳岸锚碇设计为隧道式嵌岩锚碇，设计以中风化基岩为基础持力层，锚碇抗滑移摩阻系数不小于0.6，锚碇混凝土与岩体接触面粘聚力不小于170 kPa。锚塞体单缆最大缆力2.56万t，抗拔安全系数不应小于2.0，设计围岩稳定安全系数不应小于4.0。

1.2 场区地质构造及岩土构成

据《贵州省区域地质志》及1∶20万瓮安幅区域地质调查报告，项目区域区内位于扬子准地台-黔北台隆-遵义断拱-贵阳复杂构造变形区。桥区于K36+140处垂直跨越翁绍背斜轴部，背斜轴向北北东10°，近南北向展布，桥区核部地层为寒武系下统明心寺组、牛蹄塘组，两翼地层为寒武系下统金顶山组、清虚洞组。展布北段被北东向的顶兆冲断裂及其次生断裂切割，背斜轴部错动、平移，部分背斜轴与断裂重叠而隐伏。桥区两岸岩层倾向山内，背斜北西翼(开阳岸)岩层产状：325°∠25°，发育两组节理：J1：105°∠79°，J2：36°∠81°，背斜南东翼(瓮安岸)岩层产状90°∠20°，发育两组节理Jl：48°∠77°，J2：101°∠86°。根据赤平投影分析瓮安岸岩层与J1为内倾结构面，对岸坡影响小，J2为外倾结构面，在该结构面的作用下形成瓮安岸卸荷裂隙、开阳岸岩层与J1为内倾结构面，J2为外倾结构面。在该结构面的作用下形成错落体及陡崖。场区地层为上覆残坡积层(Q4el+dl)含碎石黏土、崩塌堆积层(Q4col)块石土，下伏基岩为寒武系(∈1q)清虚洞组白云岩、白云质灰岩；寒武系金顶山组(∈1j)页岩、泥质粉砂岩、泥岩、泥质灰岩；寒武系明心寺组(∈1m)粉砂质泥岩夹泥岩；寒武系牛蹄塘组(∈1n)碳质泥岩。

2 锚塞体模型的确定

经过多次反复计算和结合施工情况，最终确定模型锚塞体按照实际体型进行1∶10比例缩小(如图1～2所示)。据此确定双模型锚塞体的间距和尺寸(两模型锚塞体尺寸相同)。双模型锚塞体尾端距离1 150.0 mm，前端距离1 350.0 mm，长均为3 200.0 mm。断面为城门洞型，底端截面高为2 158.7 mm，宽为1 550.0 mm，前端截面高为1 558.7 mm，宽为1 350.0 mm。双模型锚塞体轴线倾角均为36.2°，单缆最大缆力256.0 t。

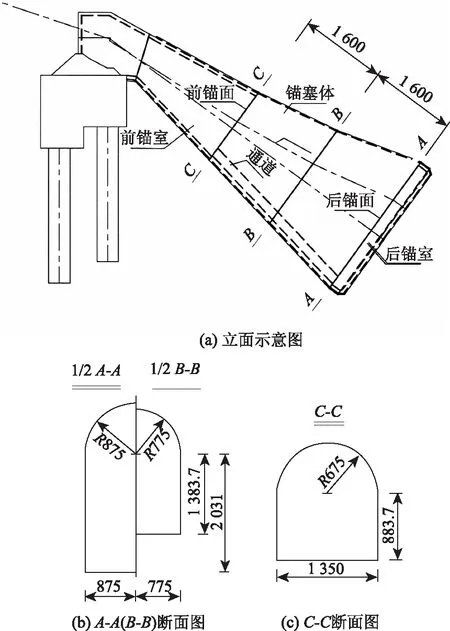
图1 模型锚塞体(单位:mm)

模型锚塞体室试点制备应符合以下规定：(1)因开州湖大桥现场条件的限制，千斤顶及位移杆等部件均采用现场焊接组装;(2)千斤顶推力面与模型锚塞体倾斜度(36.2°)始终保持垂直，模型锚塞体的荷载反力部(底部基岩)应有足够强度且需大致凿平;(3)在浇注混凝土前，应清除内壁松散的碎石及其杂物;(4)制备一定比例的混凝土试件，并进行规范养护，在模型锚塞体试验前测试其抗压强度，当其强度达到C40及以上方可进行试验;(5)以锚塞体顶端为圆心，在半径为3 m的范围外搭设试验钢架，并将位移杆搭接固定到试验钢架上;(6)锚塞体原型的受力缆索通过转换装置施加在锚塞体底部，模型试验采用千斤顶后推法加载，其受力特征相似;(7)为模拟隧道锚的实际受力状态，采用后推法进行加载试验。传力钢垫板浇注在锚塞体模型的后部，然后安装千斤顶。试验反力由在锚塞体后部的试验支硐内浇注的混凝土后座提供。考虑到模型锚塞体的超载要求，混凝土后座设计可承受荷载不小于设计荷载的20倍。

3 试验方法

3.1 试验测试原理

采用后推法测试技术对开州湖大桥进行试验测试，试验装置示意图如图2所示。在模型锚塞体尾端位置安设千斤顶及位移杆(每个模型锚塞体下位移杆 2 个、上位移杆 4 个)，沿着垂直作用方向加载，测试出模型锚塞体承载力和荷载—位移关系曲线表达式，从而计算得到模型锚塞体的极限承载力及荷载-位移关系曲线特性。

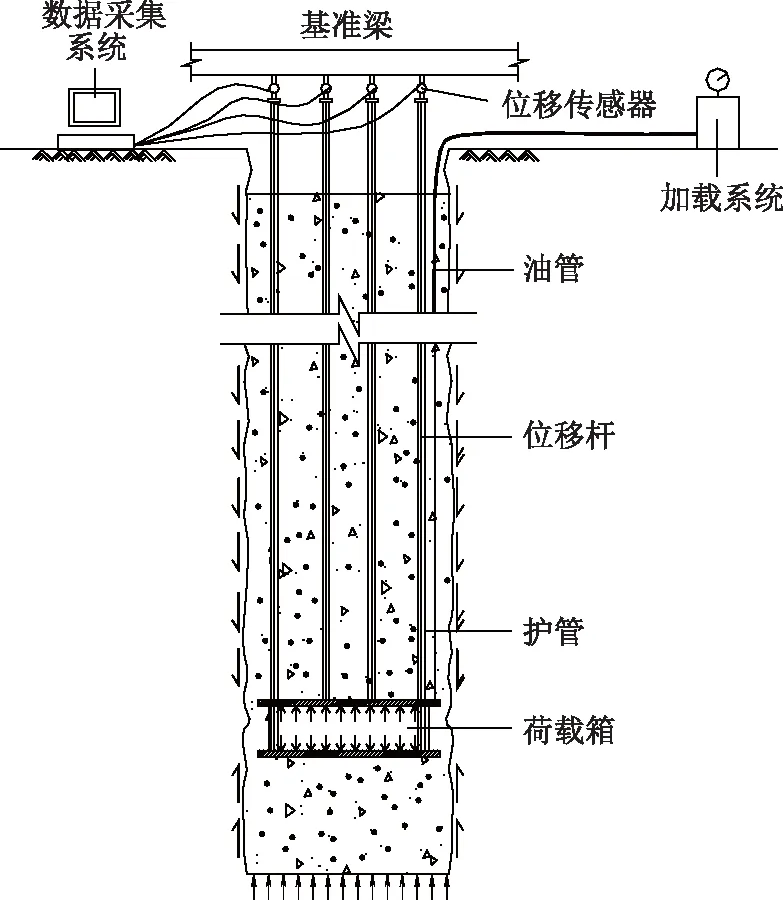
图2 锚塞体自平衡试验

3.2 加载过程

试验加载过程采用慢速维持荷载法对开州湖大桥进行测试。加载分级规定为：试验每级荷载的加载值为预估极限荷载承载力的1/10，第1级采用2倍分级荷载进行加载，第1 h内应在5，15，30，45，60 min各测读1次位移量，以后每隔30 min测读1次。卸载分级规定为：荷载最后一级荷载加载完成后，应分级将荷载卸载至0，每级卸载量按2倍分级荷载进行；每级荷载卸载后隔15 min测读1次，读2次后，隔30 min再读一次，即可卸下一级荷载，全部卸载后，隔3～4 h再读1次。荷载维持标准规定为：在加载和卸载时，应保持荷载传递均匀和连续，且无任何冲击荷载产生，每级荷载变化幅度不超过分级荷载±5%；每级荷载作用下每1 h内的位移增量不超过0.01 mm，并连续出现3次每级加载量为预估加载量的1/10，第1次按2倍分级荷载加载，见表1。每级卸载为2倍加载值，见表2。

表1 加载分级

表2 卸载分级

4 结果与分析

4.1 锚塞体加载过程分析

锚塞体的加载过程由图3位移-时间对数曲线图可见，锚塞体在5 120～25 600 kN加载下，均恒加载300 min后，各级荷载作用下位移的变化规律有所不同。总体呈现出荷载值加载时间的延长，位移呈增大的趋势，位移基本发生在15～45 min，且每级荷载值加载下，其位移最大不超过5 mm。各级荷载增大后，其位移相对增大。对比左洞和右洞的加载-位移图发现，右洞在各级荷载加载下，其位移均高于左洞，部分高于5 mm。

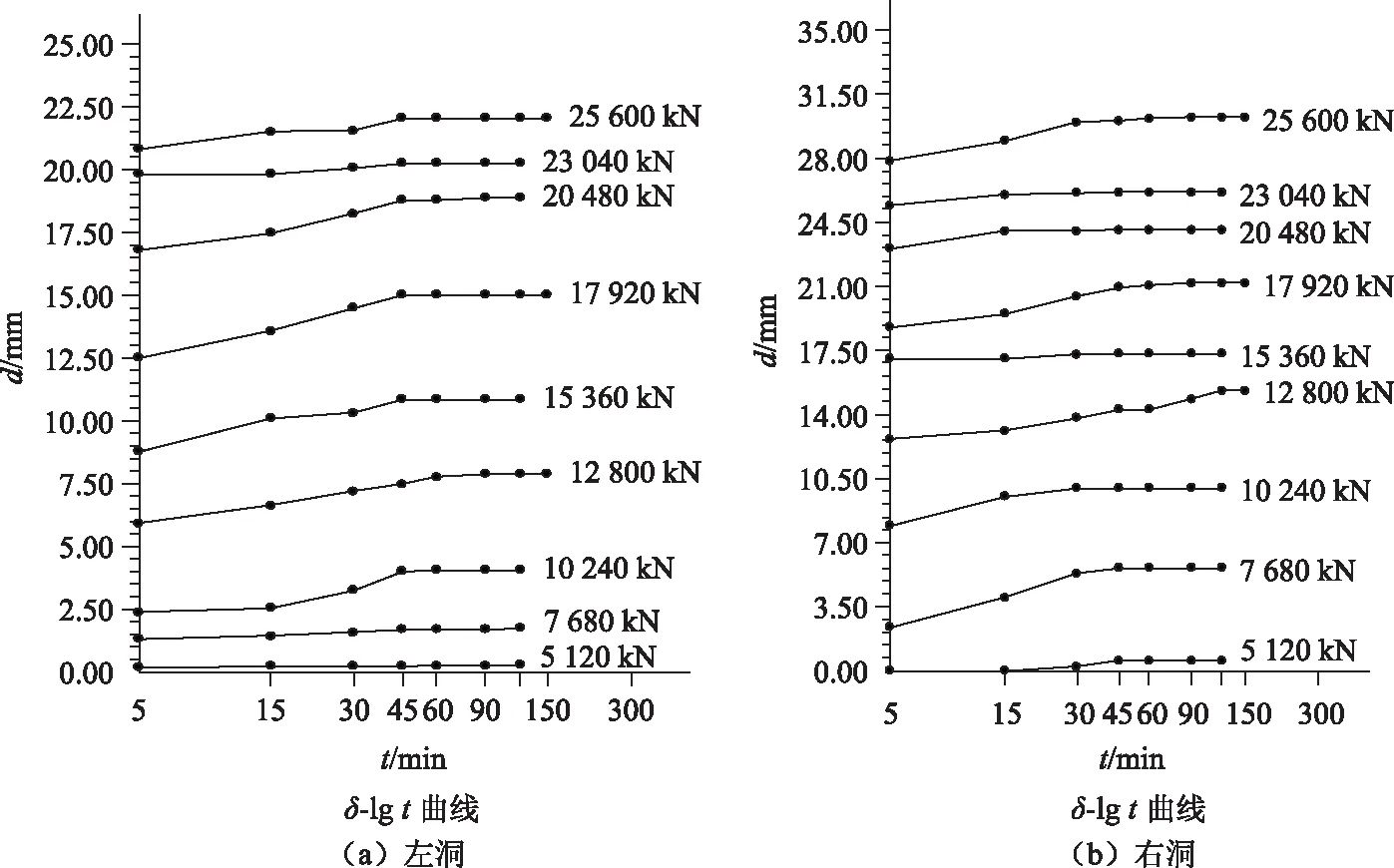
图3 位移-时间对数(δ-lg t)曲线

4.2 模型锚塞体抗拉试验

通过对模型锚塞体底部加载，其荷载-位移曲线如图4所示。

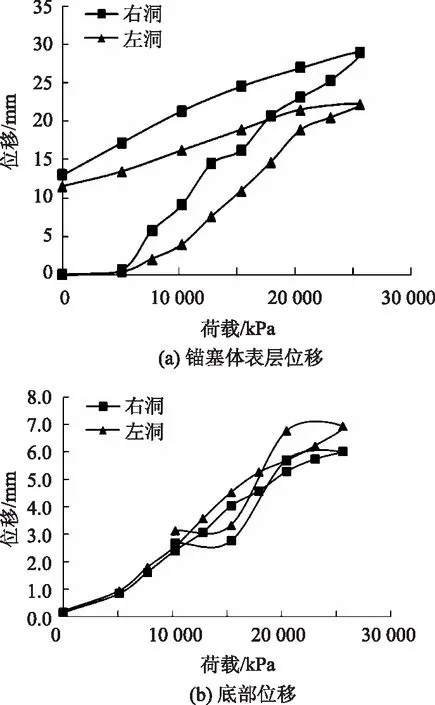
图4 荷载与位移关系

在底部荷载箱加载过程中，随着加载荷载从0增至25 600 kN时，模型锚塞体表层以及底部位移均呈增加的趋势。当极限荷载为25 600 kN，此时模型锚塞体的抗拔力为设计值的10倍，模型锚塞体及周围岩体无破坏迹象，两个模型锚塞体洞口位置出现轻微裂缝开展，荷载位移曲线为缓变形。模型锚塞体右洞表层位移为29.0 mm，模型锚塞体左洞表层位移为22.2 mm；右洞底部位移为12.9 mm，左洞底部位移为12.2 mm。在荷载箱卸载后，模型锚塞体右洞表层残留位移为13.0 mm，模型锚塞体左洞表层残留位移为11.5 mm；右洞底部位移为1.3 mm，左洞底部位移为0.95 mm。对比两个锚塞体的加、卸载过程也不难发现，右洞锚塞体在加、卸载过程中的位移均高于左洞，即使卸载完成后，仍表现出相同的规律。结合JTG/T D65-05—2015《公路悬索桥设计规范》[17]的要求和开州湖大桥的情况，该桥在运营阶段最大允许位移为11.0 mm，竖向变形为22.0 mm。通过试验发现，当锚塞体的抗拔力超过10倍设计值时，其位移量超过了允许值，经计算发现右、左洞锚塞体抗拔力分别是设计值的8倍和9倍其位移均不超过允许设计值。在设计中，要求抗拔安全系数不应小于2.0，围岩稳定安全系数不应小于4.0。本试验结果可达到8倍设计值，即安全系数达到8.0，远高于设计要求，可见开州湖大桥在运行中有足够的安全性。

4.3 锚塞体竖向抗拔承载力计算

根据DBJ 52/T 079—2016《基桩承载力自平衡检测技术规程》[18]中对于桩竖向承载力极限值的计算办法，可计算出模型锚塞体的极限承载力，见式(1)，模型锚塞体的极限承载力特征值可由式(2)计算：

(1)

(2)

式中，Qu为锚塞体的竖向极限承载力；W为锚塞体上段的自重；γ为锚塞体摩阻力的转换系数，取1.0；Qsu为锚塞体上段的极限承载力；Qxu为锚塞体下段的极限承载力；Ra为模型锚塞体的承载力特征值。

根据模型锚塞体的试验结果发现，当其位移量不超过允许位移值时，其荷载分别为20 480 kN和23 040 kN，极限荷载均为25 600 kN，模型锚塞体身的自重为547 kN。因此，模型锚塞体的竖向抗拔极限承载力特征值为12 526.5 kN。

4.4 锚塞体摩擦角和黏聚力的确定

开州湖大桥现场原位剪切试验的法向应力-位移关系曲线如图5所示，剪应力-位移(τ-us)关系曲线如图6所示。从图5发现，法向应力从0增至1 000 kPa时，其位移不断增大，即应力越大，位移基本也越大。但在右洞中，法向应力加载至800 kPa时，其最大位移比法向应力为400 kPa时低0.05 mm。从整体来看，在各法向应力增大的过程中，左、右洞位移基本呈线性变化，且右洞的位移基本高于左洞。由图6发现，当法向应力分别为200，400，600，800，1 000 kPa后，左、右洞剪切应力随位移的增加呈现出先增大后降低的变化趋势，即当剪切位移达到一定值后，混凝土试件与岩石接触面发生了一定程度的剪切破坏，其剪切应力也随之降低。

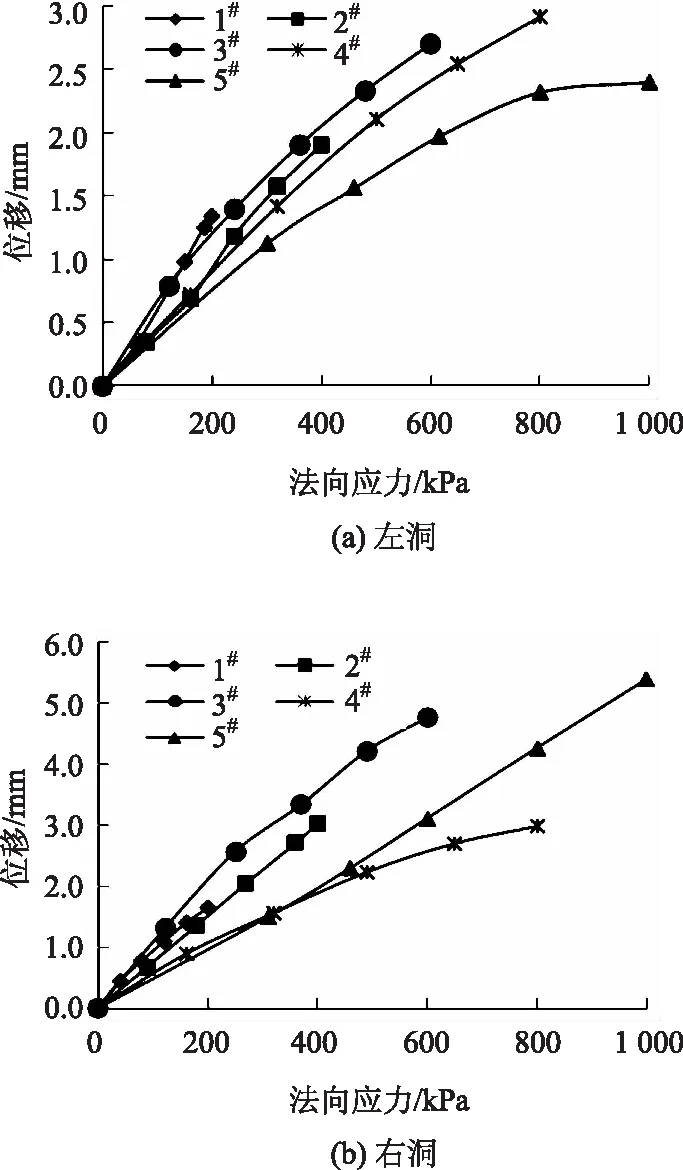
图5 法向应力与法向位移(σ-un)关系

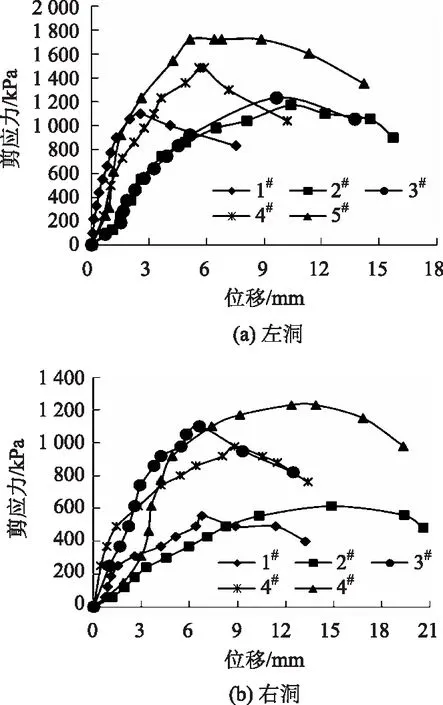
图6 剪应力与剪切位移(τ-us)关系曲线

摩擦角和黏聚力通常采用最小二乘法来确定，分别如式(3)和式(4)所示：

(3)

(4)

式中，tgφ为摩擦系数；C为黏聚力；σi为正应力值，i，…，n；τi为与σi相对应的剪应力值，i=1,…,n；n为总次数。

根据开州湖大桥的试验结果代入式(3)和式(4)，综合考虑建议左洞混凝土与岩体间的黏聚力381 kPa，右洞混凝土与岩体间的黏聚力369 kPa；左洞混凝土与岩体接触面摩擦系数0.77，右洞混凝土与岩体接触面摩擦系数1.44。结合两洞的实际情况，建议混凝土与岩体间的摩擦系数0.77和黏聚力369 kPa，高于设计中锚碇抗滑移摩阻系数不小于0.6和锚碇混凝土与岩体接触面黏聚力不小于170 kPa 的取值要求。

4.5 模型锚塞体抗拔安全系数计算

锚塞体抗拔安全系数根据JTG/T D65-05—2015《公路悬索桥设计规范》中的要求进行计算，如式(5)所示。

(5)

式中，K为抗拔稳定系数；f′为摩擦系数；A为接触面积；C′为黏聚力；P为设计值；WL为结构自重沿拉拔方向的分量；WF为结构自重垂直于滑动面的分量。

在模型锚塞体中，接触面为33.8 m2，自重垂直分量为530 kN，自重沿拉拔分量为564 kN，结合现场摩擦角和粘聚力的取值，将其代入经公式(5)，两个锚塞体的抗拔安全系数分别为5.3(左洞)和5.2(右洞)。在JTG/T D65-05—2015《公路悬索桥设计规范》中，锚塞体抗拔安全系数和围岩稳定安全系数分别不应小于2.0和4.0，本项目中，其安全系数均满足规范的要求。另外，在模型锚塞体抗拉加载试验中，右、左洞锚塞体抗拔力分别是设计值的8倍和9倍其位移均不超过允许设计值，因此，在不考虑摩擦参数时，其安全系数已经达到8.0和9.0。结合式(5)的计算结果不难发现，其安全系数满足JTG/T D65-05—2015《公路悬索桥设计规范》的相关要求，在实际运营中有足够的安全性。

5 结论

(1)锚塞体荷载值加载时间的延长，位移呈增大的趋势，位移基本发生在15～45 min，且每级荷载值加载下，其位移最大不超过5 mm，右洞在各级荷载加载下其位移均高于左洞，部分高于5 mm。

(2)在加载过程中，模型锚塞体及周围岩体无破坏迹象，两个模型锚塞体洞口位置出现轻微裂缝开展，荷载位移曲线为缓变形。在加、卸载过程中，右洞锚塞体在加、卸载过程中的位移均高于左洞，即使卸载完成后，仍表现出相同的规律。经计算发现右、左洞锚塞体抗拔力分别是设计值的8倍和9倍其位移均不超过允许设计值，远高于抗拔安全系数和围岩稳定安全系数不应小于2.0和4.0的要求，验证了开州湖大桥在运行中有足够的安全性。

(3)试验结果建议混凝土与岩体间的摩擦系数为0.77和黏聚力为369 kPa，采用各模型锚塞体的摩擦系数和黏聚力，确定两个模型锚塞体的的安全系数分别为5.3(左洞)和5.2(右洞)，满足JTG/T D65-05—2015《公路悬索桥设计规范》中，锚塞体抗拔安全系数和围岩稳定安全系数分别不应小于2.0和4.0的要求。