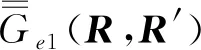几种格林函数方法的形成及其应用比较研究
2021-09-08雒向东赵宇杰
雒向东,张 明,海 波,赵宇杰
(1.兰州城市学院 电子与信息工程学院,甘肃 兰州 730070;2.甘肃高师学报编辑部,甘肃 兰州 730070)
1 基本理论
20世纪30年代中期,汉森在解决某些电磁问题时,首先引进了三类矢量波函数,分别记为L,M,N,它们都满足齐次亥姆霍兹矢量方程[1,2].如图1所示在直角坐标系中对矩形波导选取z轴单位矢量作为领示矢量c,矩形波导内电磁场矢量波函数有如下形式[3,4]:
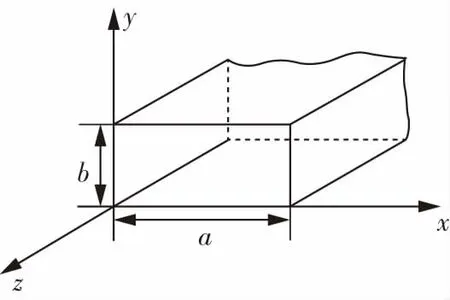
图1 矩形波导
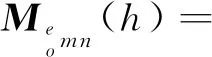
(1)
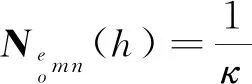
(2)
(3)
(4)
2 磁型格林函数方法
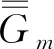

(5)

(6)
定义域为:0≤x≤a,0≤y≤b,-∞≤z≤∞.
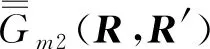
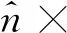
(7)
假设

(8)
用函数Nem′n′(-h′)作为(8)式的前标积可得
(9)
(9)式左边积分为
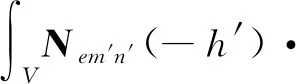
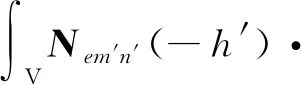
(10)
由于径向R′位于体积V内,(10)式中面积分等于零.函数∇′×N′是对带撇变量x′,y′,z′定义的.
(9)式右边积分为
(11)
将(10)、(11)式代入(9)式得
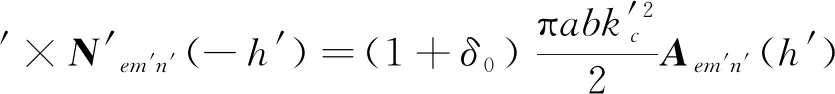
(12)
解出系数

去掉本征值上的撇号,保留函数M′上的撇号,(12)式可改写成
(13)
用类似方法,用Mom′n′(-h′)作(8)式的前标积,同样可推得
(14)
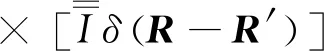

(15)
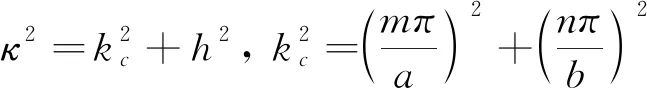
假设
(16)
将(15)和(16)代入(6)式得
(17)
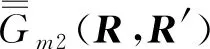
(18)
(19)

上行符号对应z>z′,下行符号对应z 在z=z′处,对不连续磁型并矢格林函数有 (20) (21) (22) 利用单位阶跃函数 得 (23) 利用 得 (24) 由(21)式此方程又可写成 (25) (26) (26)式中上行符号适于z>z′,下行符号适于z (27) (28) Lomn(h)定义为 (29) Sx=sinkxx,Cx=coskxx,Sy=sinkyy,Cy=coskyy. Lomn(h)函数组本身以及与其他两组函数正交关系如下[3]85-86: (30) (31) (32) 可见Lomn(h),Nomn(-h′)在空域内不正交,但包括h域在内时就正交,正交关系如下: (33) 根据Ohm-Rayleigh方法,假设 (34) 用Lom′n′(-h′)对(34)式作前标积可得 Lom′n′(-h′)·Memn(h)Bemn(h)+Lom′n′(-h′)·Nomn(h)Comn(h)] (35) 同理用Mem′n′(-h′)、Nom′n′(-h′)对(34)式分别作前标积可得 (36) (37) (38) 假定 (39) 把(38)和(39)式代入(27)式得 (40) 把Lo和No分成两部分 Lo=Lot+Loz,No=Not+Noz Lot和Not代表横向分量,Loz和Noz代表纵向z分量. (41) (42) (43) (44) 可用Not,Lot分别表示Noz,Loz,对带撇的函数可同样的表示,有 利用这些关系(40)式可改写为 进一步可推得 (45) 从(38)式可得 (46) (47) 计算可得 (48) 故得 (49) (49)式与(26)式是一样的. (50) (51) (52) (53) (54) 把(54)式代入(50)式得 (55) Φ是电标量位函数的矢量形式,引入规范条件[3]89 (56) 把(50)、(52)、(55)式代入(51)式可得 (57) (58) 由于三组矢量波函数在空域和h域内是正交性,故可确定(58)式中的三个系数A,B,C. 用Lom′n′(-h′)对(58)式作前标积,等式左边为 等式右边为 最后可推得得 用Mem′n′(-h′),Nom′n′(-h′)对(58)式分别作前标积可得 (59) 假定 (60) 将(59)和(60)代入(57)式得 利用 ∇×Lo=0, ∇·Lo=-kxkxSxSye-ihz-kykySySxe-ihz-h2SxSye-ihz, ∇∇·Lo=-κ2Lomn(h), ∇∇·No=0 代入(60)式得 (61) 对(56)式取梯度得 (62) 代入(55)式得 (63) 将(61)代入(63)式得 整理最后得 (64) (64)式与(40)式相同.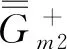
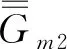
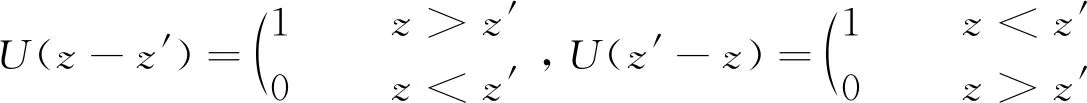
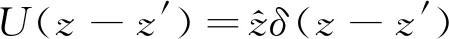

3 电型格林函数方法
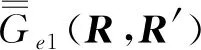
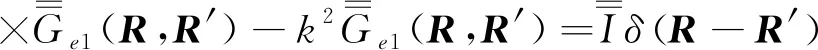

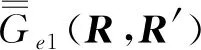
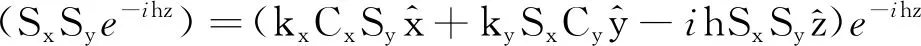
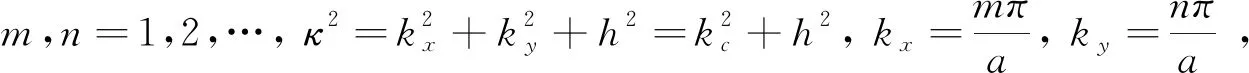
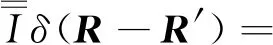

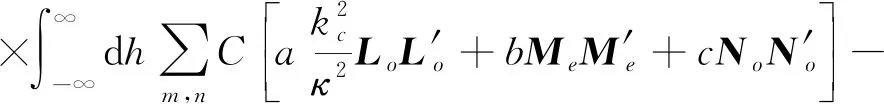


4 位型格林函数方法

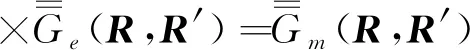


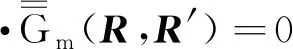
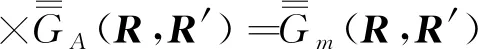
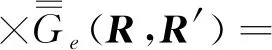
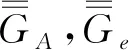
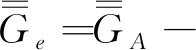
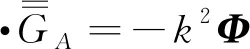
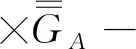
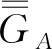
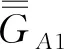
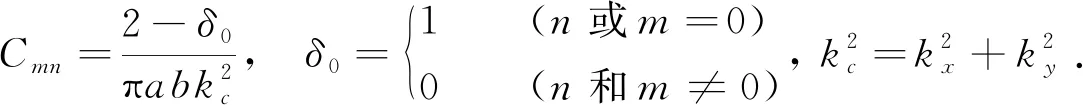
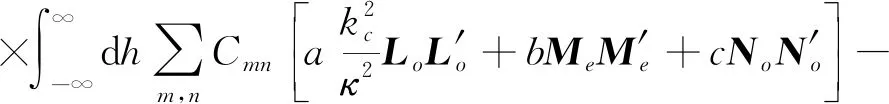
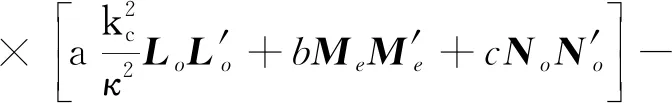
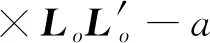

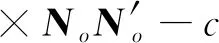
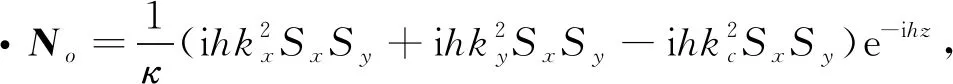
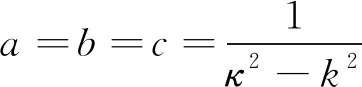
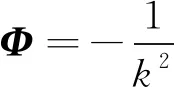
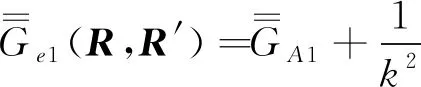
5 磁型、电型和位型格林函数方法应用比较