二级倒立摆DE优化控制

鲍广喜

(安徽工程大学 计算机与信息学院，安徽 芜湖 241000)

0 引言

模糊控制方法是以专家知识为基础模拟人类推理方式一种近似推理控制方法.其适应性强、容错性和鲁棒性好等优点使得它在各个领域得到了广泛的研究与应用[1-2].闫安等人针对单轨双轮机器人在静止情况下存在固有静不稳定的问题，提出了一种基于模糊强化学习的控制方法，采用模糊理论泛化动作空间，改善控制精度，并使控制输出连续[3].针对传统电力应急指挥系统自动控制策略在控制系统运行时控制指令传输所需时间过长的问题，刘军等人设计了一种基于模糊控制器的电力应急指挥系统自动控制策略[4]，将模糊器结构中的输入、输出物理量转换为模糊量,计算转换后模糊量的隶属度,得到模糊器中的近似算法,构建出一个前向树,最终得到系统的控制方案进而实现了自动控制.为了探索出提高快速反射镜伺服性能的控制方法，利用模糊控制和PID控制相结合的方法，高歆杨等人成功地设计了一种快速反射镜伺服控制器，该模糊控制器既继承了PID易于工程实现的优点,又具有可自适应调整定控制参数的特点，从而可提高现有快速反射镜的伺服性能，更好地适应各类运行工况[5].然而由于其本身过度依赖专家知识和经验，也就是在设计规则和隶属度函数时完全凭经验设置，在这过程中，知识和经验的不确定性会降低控制精度并使得系统动态性能变差.为此系统中的参数需要进一步优化调节.

通常情况下，模糊系统中的参数是由输入输出变量个数和模糊划分直接决定的[6].在输入输出变量个数确定时，如果模糊划分越细，那么控制效果会更好，但是其规则和参数会成级数增加.因此如何在大量的参数中找到更加合理的参数成为解决最优模糊问题的一个难点.为了找到合适的参数，文献[7]分别运用GA，蚁群算法(ACO)和RNA-GA对隶属度中参数进行优化并取得良好的控制效果.此外，郭卫等人引入遗传算法对方法进行参数优化，使其更好地满足速比控制的要求[8].针对开关磁阻电动机非线性、难以建立精确数学模型的问题，黄志凡在文献[9]中利用粒子群优化算法对模糊控制器进行调参，仿真实验验证了粒子群优化算法优化模糊控制器参数的有效性.在此基础上，基于变异、交叉和选择的差分进化(DE)算法是启发式进化算法.相比其启发式算法，该算法凭借其良好的全局搜索能力和收敛特性在最近几年得到广泛应用和关注，尤其是解决高维寻优问题时，其效果更加明显[10].

二级倒立摆是一种不稳定系统，它是许多控制对象的简化模型[11].对它的控制可以用来检测控制方法的有效性.为此，本文根据其倒立摆特性，设定相应的目标函数，并运用DE算法对模糊控制器参数进行优化调节，将优化后的控制器应用到倒立摆的摆角控制.实验证明优化后的模糊控制器控制性能更好.

1 DE优化算法

DE优化算法以变异、交叉和选择三种基本操作为基础进行迭代寻优，是一种实数编码方式的全局优化算法.

1.1 种群及个体表述

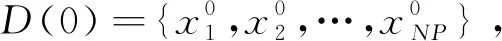
(1)

其中xj,max和xj,min分别表示第j维的上下界.

1.2 变异操作

在一个父代种群中随机进行选择，选出两个不同的个体向量，相位下降产生差分向量，并将差分向量赋予一定的权值，进而与另一个父代种群随机选出的向量相加，产生变异个体[12].任意一个父代种群中的目标向量xi,变异向量生成公式如下：

vi=xr1+F·(xr2-xr3),i=1,2,…,NP

(2)

其中{xr1,xr2,xr3}是父代种群中三个不同的随机个体，并且xr1≠xr2≠xr3，F称作缩放因子介于[0,2]之间.太小的缩放因子易导致收敛过早陷入局部最优，太大的缩放因子容易导致收敛性降低.经验证要想得到最好的收敛效果，F的取值范围应为[0.5,0.9].

1.3 交叉操作

交叉操作可实现种群多样，将变异向量vi的各维分量与目标向量xi的各维分量进行随机重组，产生一个新的交叉向量ui=[ui,1,ui,2,…,ui,D]，其生成公式如下：

(3)

其中，0≤p≤1表示随机数；randD∈[1,D]表示随机整数；Pc表示交叉概率.

1.4 选择操作

“贪婪”选择模式是DE算法通常采用的一种模式[13]，即仅当交叉向量ui比目标向量xi具有更好的适应度值时，ui才将会变为一个下一代的新个体.反之xi将保留到下一代种群中.设minf(x)为最优化问题，那么选择操作表述公式如下：

(4)

1.5 算法流程

基于以上描述理论，以目标函数最小值求解为例，算法描述如下：

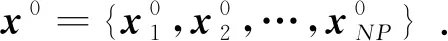
Step2：迭代次数更新g=g+1，目标个体索引号设置为i=i+1.

Step3:除了目标个体之外，再从种群中随机选取三个与之不同的个体，按变异公式生成一个新的变异个体vi.

Step4：按交叉公式生成一个新的交叉个体ui.

Step5：计算适应度值并执行选择操作.

Step6：更新目标个体i=i+1返回Step3直至i=NP；否则执行下一步.

Step7：判断是否大于G，若不满足返回Step2继续迭代，满足则算法结束.

2 模糊控制器参数优化

2.1 模糊控制器建立

依据二级倒立摆系统的性质，以误差和误差变化率为输入变量，以控制力为输出变量建立一个模糊系统，输入输出变量采用在上五级模糊划分，并采用高斯型隶属度函数.相应的模糊规则如表1所示.

表1 模糊规则

2.2 目标函数设置及其参数优化

由于模糊规则库知识是给定的，只需调节输入输出变量的隶属度参数即可[14].为了达到更好控制目标，我们根据被控对象的物理特性设定相应的目标函为：

(5)

其中x,θ1,θ2分别表示小车位移、下摆角和上摆角.

根据给定目标函数公式，运用DE优化算法[15]对上一节建立模糊控制器中的隶属度参数进行调节，相应的优化步骤和系统框图如图1所示：

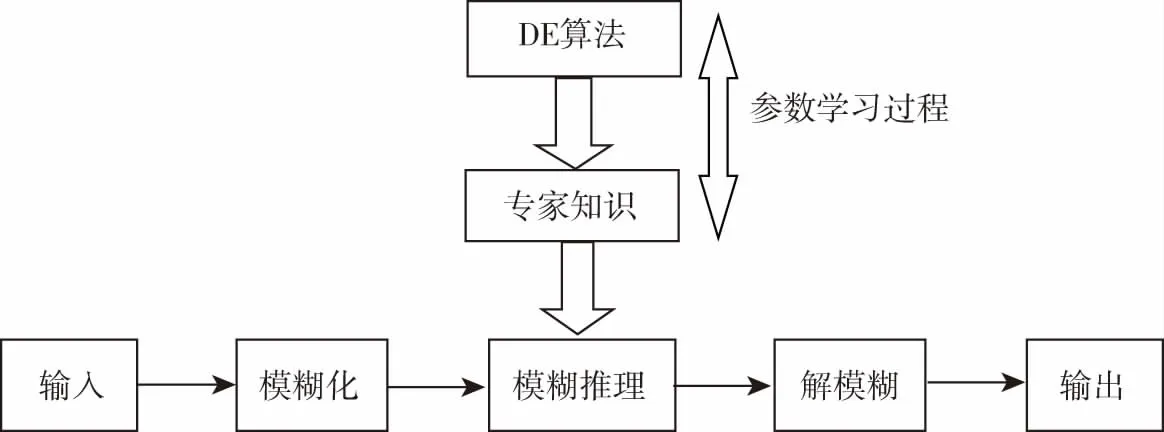
图1 模糊控制器优化框架图

Step1：设定输入输出变量各个模糊划分下隶属度函数参数范围.

Step2：初始化DE优化算法参数(G=100,F=0.85,Pc=0.5).

Step3：随机产生NP=30组参数，计算每组参数在倒立摆控制中目标函数值.

Step4：选择最好一组参数,执行变异操作和交叉操作，然后生成30组新的参数，最后计算出目标函数值.

Step5：进行迭代循环直至满足g=G=100，并最终找到最优参数值.

3 二级倒立摆仿真实验

3.1 系统分析

二级倒立摆属于典型的非线性动态不稳定系统，通常用来检查控制方法的有效性.如图2所示，该装置由一个小车和两台摆杆组成，用前后力作用于小车，使得摆杆垂直不倒.其相应的动态模型为：

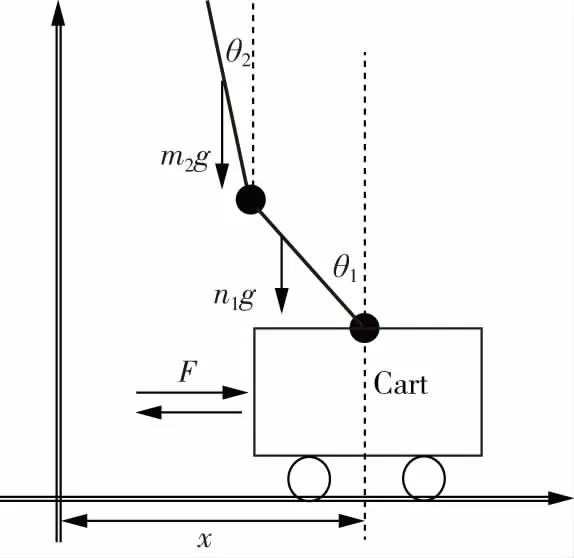
图2 二级倒立摆系统

(6)

(7)

(8)

(9)

3.2 仿真结果

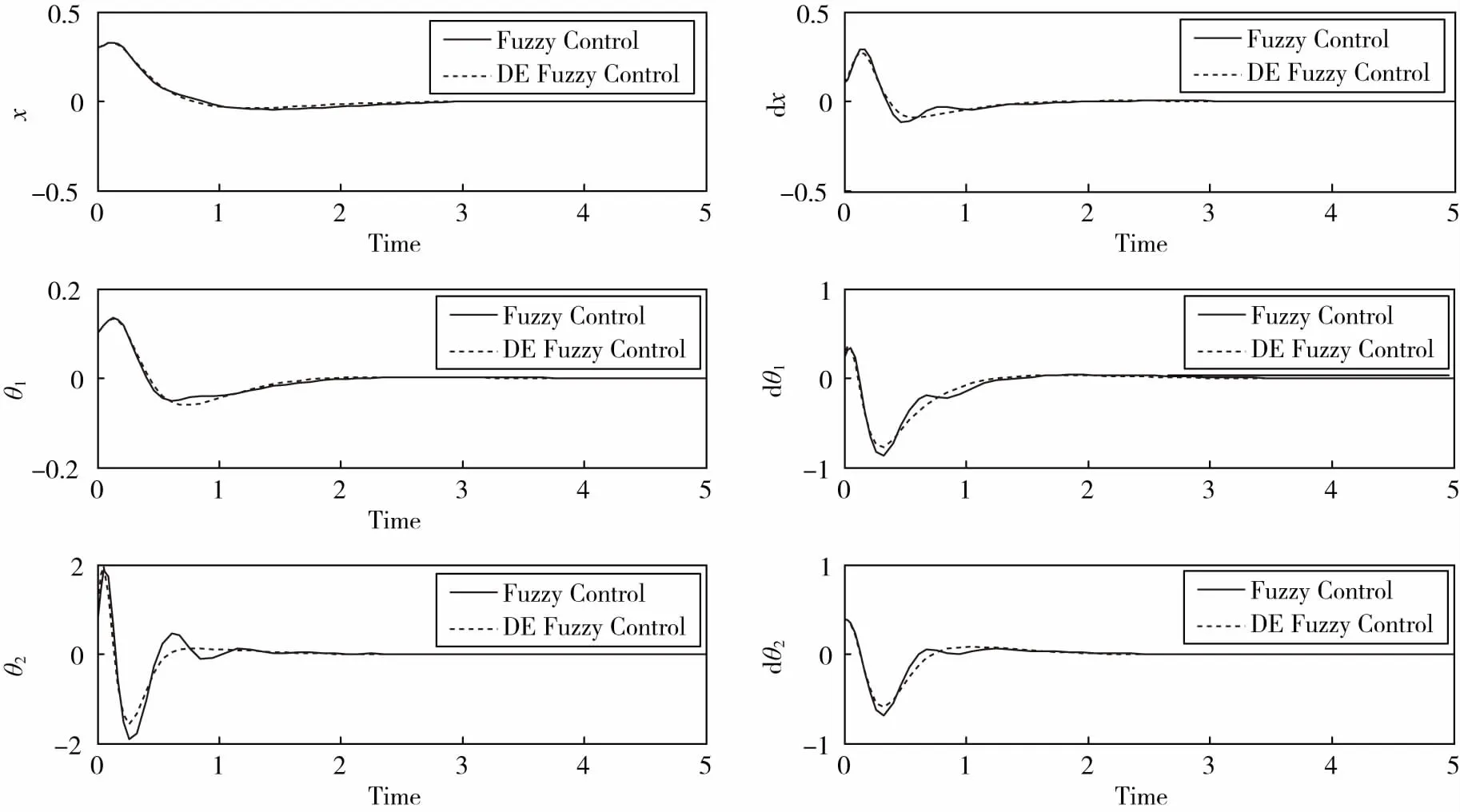
图3 二级倒立摆仿真结果比较

4 结论

由于DE优化算法在全局搜索能力和解决实数优化问题突出优势，针对模糊控制器本文提出了一种基于DE优化算法的参数调节方法.由二级倒立摆的物理特性，设定相应的适应度函数，对建立模糊控制器的参数进行优化调节.随后采用优化后的控制器参数对二级倒立摆进行仿真测试，实验结果表明，优化后的控制器比没有优化的控制器在性能上有了显著提高，从而进一步证实了该方法的有效性.除此之外，该优化和控制方法也可以用在生产调度，参数估计以及其他控制领域等.