基于目标优化的自动驾驶决策规划系统自动化测试方法

邢星宇，吴旭阳，刘力豪，陈君毅，余卓平

（同济大学汽车学院，上海 201804）

在自动驾驶汽车飞速发展和广泛应用的进程中，自动驾驶事故屡有发生，其安全性成为自动驾驶技术发展的关键。合理的测试和验证方法是发现系统缺陷并优化系统功能，从而避免类似事故的重要手段［1］。决策规划系统位于自动驾驶系统信息传输与处理过程的中间部分，它需要处理复杂的外界环境信息，并直接影响控制执行系统的表现，因此决策规划系统测试在系统级测试阶段占有重要地位。针对决策规划系统的测试存在诸多挑战。首先，决策规划系统需要根据周围环境变化做出实时判断和决策，因此对决策规划系统进行验证只能通过在环测试方案。此外，目前的自动驾驶决策规划系统大多是基于独立功能切换的系统［2］，不同的功能单元之间切换逻辑条件繁杂且敏感；部分以机器学习为基础的决策规划系统则具有一定的不可解释性，其行为具有概率分布的特点。以上问题都增加了决策规划系统测试的难度和复杂性。

为解决上述问题，在基于场景测试方法的基础上，有学者提出了基于数据优化搜索的场景测试方法。Bühler等［3］利用启发式优化算法，使用泊车质量相关的评价指标设计成本函数，自动迭代修改测试泊车位形状，以挑战自动驾驶系统的泊车算法。Abdessalem等［4］采用遗传算法测试了行人检测系统。Tuncali等［5］采用模拟退火算法，设计了基于鲁棒性评价指标的成本函数，对带有机器学习模块的自动驾驶系统进行了搜索测试。Klischat等［6］使用进化算法，借助可达性分析方法，通过改变交通参与者的初始状态来寻找使可达域更小的关键场景。基于目标优化搜索的场景测试方法针对性更强，结合仿真测试平台及自动化测试工具能够高效地完成大规模测试，在系统开发阶段能够为功能快速迭代优化提供支持，弥补了基于数据分析方法的不足。但已有的研究工作较少涉及决策规划系统测试，且在研究多种优化搜索算法的具体测试效果方面仍需深入。

针对上述问题，本文提出一种基于目标优化搜索的决策规划系统自动化测试方法，能够针对性地为被测对象生成关键场景并实现自动化测试；本研究基于决策规划系统硬件在环仿真测试平台，对方法的有效性进行了验证；并进一步对比分析了贝叶斯优化算法（Bayesianoptimization，BO）、遗传算法（geneticalgorithm，GA）、随机搜索算法（random searching，RS）三种搜索算法在生成关键测试场景时的效果，探索面向不同实际测试需求的最优算法。

1 目标优化场景生成与自动化测试

仿真场景测试基于真实交通环境包含的各类要素及其特征进行抽象和简化，从而构建出满足测试需要的仿真测试场景。但由于场景中要素数量众多、要素参数连续变化等问题，场景数量呈现爆炸式增长的趋势，穷尽式测试方案是不具备可操作性的。同时，随机生成的大多数测试场景是“低风险的”正常行驶场景，测试价值较低，测试更应关注使车辆在特定层面出现临界状态的关键场景。本文中的关键场景主要是指安全性相关的危险场景。关键场景的产生可能有系统外部和内部的原因，一方面，它们可能由外部交通参与者的危险驾驶行为导致。另一方面，被测系统自身的缺陷和决策规划的非线性逻辑，也会形成关键场景。

本文将被测对象视为黑箱，以场景参数空间作为输入，基于被测对象行为表现的安全性评估作为输出，将关键场景生成与测试问题转化为目标优化问题。基于优化算法不断寻找“最值”的性质，有目的性地搜索符合需求的测试场景。同时，基于仿真环境下的自动化测试工具，可以实现自动化迭代计算，提高场景测试效率。

1.1 关键测试场景生成问题定义

本文的核心思路是将场景测试问题转化为目标优化问题，首先确定问题的输入、输出以及连接输入与输出的场景生成方法。本文在场景描述时，使用功能场景、逻辑场景、具体场景的三层场景结构［7］。关键场景生成与测试的方法框架如图1所示。

图1 关键场景生成与测试框架Fig.1 Frameworkofcriticalscenariogenerationandtesting

设D代表逻辑场景参数空间，基于在环仿真平台，定义仿真函数sim的输入是D中的场景参数向量X，输出为原始仿真结果，如自车和其他交通参与者的运动轨迹等。另外，定义成本函数f，其输入为原始仿真结果，输出为成本函数值v，σ为设定的成本函数危险阈值。由此，场景参数向量X和成本函数值v通过在仿真平台中运行的仿真实验形成了如式（1）所示的映射关系。由于场景存在复杂性，且决策规划系统存在不确定性，X和v的映射关系是一个典型的黑箱问题。

综上，面向决策规划系统的关键场景生成问题，可以转化为如式（2）所示的在给定的场景参数空间D下，寻找特定的场景参数向量X，将成本函数值v最小化的优化问题。

对于该优化问题，搜索算法表征了寻找关键场景的策略。本文的黑箱存在两方面特性：其一，仿真软件的不确定性以及仿真消息可能发生的随机延迟或丢失使成本函数值存在一定随机误差，降低了成本函数的导数计算的可靠性。其二，实时硬件的引入增高了单轮仿真实验的时间成本。因此，通过对比不同搜索算法的随机误差处理策略和效率，本文最终选择了贝叶斯优化算法和遗传算法作为搜索算法。

1.2 基于贝叶斯优化算法的关键测试场景生成

在使用贝叶斯优化算法进行关键场景搜索时，需要结合黑箱特性设计算法参数。考虑到模型表征非线性函数以及处理随机误差的能力，本文选用了如式（3）所示的高斯过程建模代理模型。其中先验均值函数μ(x)取默认值0，协方差函数k(x，x')如式（4）所示选用了5/2内核和较大的尺度参数l，增强了对非平滑函数的建模能力。采集函数α(x)如式（5）所示，采用了基于预期改进的策略，其中ymax是在当前测试中观察到的评价指标最大值，f(X)是对下一个场景评估点X的预期值。该策略在增加提升量的同时也保证收敛速度，且在当目标函数随机误差较大时可以提高回归过程的鲁棒性。更新方法选用了边际估计方法，通过使用log边际似然函数logp(yi|x i，β，l，σ)进行更新，提高了系统处理不确定性的能力。

1.3 基于遗传算法的关键测试场景生成

在使用遗传算法进行关键场景搜索时，需要结合优化问题特性选择具体参数。对于编码方式，传统的二进制编码以离散方式搜索，可能使欧式距离较小的两组场景参数存在着较大的汉明距离，进而削弱交叉和突变操作的效果，使算法不能有效探索整个场景参数空间，陷入局部优化之中。因此本文采用实数编码的方式，以在连续域上搜索整个场景参数空间。对于交叉方法，本文采用模拟二值交叉方式以结合二进制编码的搜索特点，提升产生新的场景参数组合的概率。对于变异方法，考虑场景参数组合作为染色体的特性，本文采用高斯突变算子，对染色体上每个基因即具体的场景参数都进行在一定阈值范围内的概率变异。对于选择方法，本文采用了锦标赛选择方法以提高收敛速度。

对于遗传算法需要设置的其他参数，考虑本文中单轮仿真实验的评估时间成本较高，因此种群规模不宜过大，代数也应被控制在一定合理范围内。最终选择的遗传算法参数如下。种群规模：10，进化代数：40，交叉概率：0.9，变异概率：0.1。

1.4 自动化仿真测试框架

本文设计的自动化仿真测试框架如图2所示，整体可分为基础仿真实验配置和自动化测试两个部分。其中基础仿真实验配置部分初始化仿真测试所需要的各个组件以及静态仿真环境；在自动化测试部分则通过管理场景的终止条件以及动态对象的生存销毁状态来控制仿真实验的迭代运行。

图2 自动化仿真测试框架Fig.2 Framework of automatic simulation testing

对于基础仿真实验配置部分，首先初始化并连接仿真服务器和仿真客户端，其次初始化仿真静态环境等基本仿真配置。

对于自动化测试部分，首先由优化搜索算法选择特定的场景参数组合，在已初始化的仿真静态环境中通过动态对象生存管理器配置相应场景参数后开始进行仿真实验，被测决策规划系统不断从仿真客户端中订阅感知信息流，并发布控制信息流。当仿真实验满足预先设定的场景终止条件时，从仿真实验中获取原始仿真结果，并由对象生存管理器销毁动态对象，由此结束当前轮次仿真实验。优化搜索算法在分析了基于相应仿真结果计算出的成本函数值后，给出下一个建议的场景评估点，即待评估的场景参数组合，再通过动态对象生存管理器根据场景参数重新生成对象并进行新一轮仿真实验。在整个过程中，被测决策规划系统一直维持在运行状态。

2 实验验证

本节基于自动化在环仿真测试平台进行仿真测试，被测决策规划系统以硬件形式接入测试环境。基于对决策规划系统特性的分析，选取典型功能场景，分析场景参数和参数范围得到相应的逻辑场景作为测试输入。以评价指标为基础并结合规避无效场景的条件构建成本函数。接下来简要介绍实验方案部署情况。

2.1 测试平台搭建

为了提供接近决策规划系统实际运行条件的测试环境，同时保证测试效率，本文设计并搭建了基于硬件在环的决策规划系统测试平台，能够实现仿真环境与被测硬件系统的信息交互，达到在环测试的目的。平台包括硬件层、仿真层和数据层。硬件层主要包括被测决策规划系统硬件、感知信息输入接口、控制信息输出接口。本文所测试的决策规划系统为团队自行开发的面向城市自动驾驶功能的决策规划系统，具备循迹、跟车、换道、避障等功能，可满足实际仿真测试时的基本需求，该决策规划系统被部署于型号为ARK-3500的工控机中。仿真层为面向自动驾驶测试的仿真测试环境。考虑决策规划系统对场景输入信息的多样性需求，本文采用CARLA开源仿真平台作为仿真软件，提供环境要素模型、车辆动力学模型和传感器模型。本文主要研究决策规划系统性能表现，为避免感知系统的影响，本文采用理想传感器模型，基于仿真数据接口构建了导航定位和对象列表等环境信息输入方案。数据层主要用于仿真层与硬件层之间的信息传输，并管理整个自动化仿真测试过程。其将来自仿真层的感知信息和车辆自身状态信息通过软件的仿真数据接口导出，相关数据在被编码为仿真消息后，通过逻辑接口和物理接口传输至被测硬件。

在仿真环境中，对于环境车辆的行为实现方式，主要通过基于规则的行为决策和基于PID（proportion-integral-derivative）的轨迹跟踪实现。对于车道保持行为，通过使用横向和纵向的PID控制器跟随特定路径点实现；对于换道行为，环境车需检测换道触发距离是否满足设定阈值，并通过局部规划器，配合PID控制进行换道轨迹跟踪。

2.2 仿真场景选取

所要测试的功能场景可以通过多种手段确定，如对被测系统进行安全分析以获得潜在的危险场景［8］，或根据测试需求确定。本文选取了一个典型的低速车辆切入场景进行方法验证。在晴朗白天的高速公路三车道上，自车跟随前方车辆行驶，经过一段时间，相邻车道车辆切入到自车前方。在该场景中，自车需要在短时间内完成跟车-制动避障-跟车的连续行为切换。针对选定的功能场景，本节按照道路拓扑结构、环境信息、自车以及其他交通参与者的顺序分析所需的场景参数。同时为控制测试中的影响因素，对其他环境要素进行适当简化。考虑具体的测试需求和不同场景参数的相关性，最终确定场景参数设置（图3）。

图3 邻车道车辆切入功能场景示意Fig.3 Schematic diagram of functional scenario：cut-in

在确定场景参数后，需要进一步确定每个场景参数的取值范围构建逻辑场景。参数范围的选取一般基于自然驾驶数据的分析获取参数范围及其分布情况，同时结合被测对象特点和测试需求进行确定。考虑到参数范围的选取并不是本文的研究重点，且并不影响本方法的有效性，因此本文主要结合系统的功能需求和一般经验制定场景参数范围，并设参数为均匀分布，最后通过预实验最终确定场景参数范围，如表1所示。对于自车初始速度的设定，考虑到其具备自主规划速度和轨迹的能力，为减少人为干预，同时压缩自车由完全静止启动所需要的时间，在实验中将其初始速度设定为2 m·s-1，测试启动后，自车将加速跟进前车，并保持合理车间距，或择机进行换道，自车加速度范围为±3 m·s-2，最高车速可达到12 m·s-1。

表1 逻辑场景参数范围Tab.1 Parameter range of logical scenario

2.3 成本函数构建

成本函数作为本方法中搜索算法的优化目标，需要客观反映测试的总体目标和需求。本文重点关注决策规划系统的安全性，因此成本函数需要基于安全性评价指标进行设计，同时要求有一定连续性，以量化每个场景参数组合的关键程度，进而有效地应用搜索策略。此外，成本函数需要考虑排除无效场景，即期望的系统行为并未发生的场景，以提高测试效率。

对于本文研究的场景，碰撞时间（time to collision，TTC）是衡量危险程度的重要指标，且具有一定的连续性［9］。在场景动态变化过程中，自车和切入车TTC的最小值可以认为是场景最危险的时刻，能够反映决策规划系统在不同具体场景下的行为安全性，因此选择以最小TTC值为基础构建成本函数。针对无效的场景，在本文中主要指切入车切入到自车后方的场景、切入车与前车发生碰撞的场景以及TTC一直为负值的场景。

综上，本文最终设计了如式（6）所示的成本函数值公式。当场景无效时，对于GA，成本函数值设置为惩罚值α。对于BO，为了不破坏代理模型模拟的高斯分布，成本函数值设置为无效值。另外，当场景有效时，BO算法对应的成本函数为-min(TTC)，从而将最小值优化问题转化为了最大值优化问题，进而纳入BO的算法框架。

2.4 关键具体测试场景生成与测试结果

Olsen等［10］将切入场景划为三个危险级别，无危险1级（TTCmin＞3 s）、紧急2级（1 s＜TTCmin≤3 s）以及濒临碰撞3级（TTCmin≤1 s），本文将2级和3级场景设为关键场景。分别采用贝叶斯优化算法和遗传算法进行100轮迭代优化，并与基线算法进行了初步比较。本文基线算法选择随机搜索，根据不同参数的参数范围设定合适的采样粒度构建参数空间，之后采用均匀分布在参数空间中进行随机采样。结果如图4所示。

图4 优化搜索算法成本函数值迭代结果Fig.4 Results of cost function by optimization algorithms

横轴为迭代轮次，纵轴为成本函数值。可以看出相比无优化的随机搜索，BO算法和GA算法更容易生成使被测系统发生紧急或危险状况的场景。且随着迭代次数增加，成本函数会逐步集中于TTCmin≤3 s的范围内。但需要说明的是，试验结果并没有显示出显著的收敛性，这主要是由于本试验采用了硬件在环的测试方式，引入了部分仿真消息随机延迟或丢失导致的不确定性；此外，由于被测决策规划系统采用了动态规划加二次规划的方案进行轨迹和路径规划，每次求解的时间根据硬件状态存在一定波动，使得系统在相同的参数输入下输出结果产生波动。上述不确定性导致了算法无法稳定的向特定值收敛，但总体而言，优化算法相比随机搜索，有效地提高了生成危险场景的效率。未来，可以通过多次测试取均值的方式，或引入概率统计方法，对不确定性进行刻画和表征，提高算法的适用性。表2、表3展示了BO、GA算法测试得到的部分关键场景参数结果。

表2 贝叶斯优化算法生成的关键场景参数组合示例Tab.2 Examples of critical scenario parameter combinations generated by the Bayesian optimization algorithm

表3 遗传算法生成的关键场景参数组合示例Tab.3 Examples of critical scenario parameter combinations generated by the genetic algorithm

3 算法效果对比

基于本文所提出的关键场景优化搜索生成方法，按照硬件在环仿真测试的试验方案，分别应用贝叶斯优化算法、遗传算法和随机搜索算法进行了方法验证，并从方法的搜索效率和搜索质量两方面对算法效果进行了比较。

在搜索效率方面，以预先设定的最大迭代次数400轮作为实验终止条件，并进行多次测试取平均值。4次试验中，BO、GA和RS方法生成场景和测试所得不同成本函数的平均频次分布如图5所示。以关键场景对应于成本函数值小于3 s的场景为例，三种算法搜索到的关键场景数量比值是GA：BO：RS=3.3：2.5：1.0。

对生成的场景及测试结果做进一步分析。当TTCmin≤0.2 s时，即认为自车与切入车发生了碰撞。在4次400轮迭代测试中，BO算法共生成了3次碰撞场景，GA算法生成6次碰撞场景，RS算法则没有产生碰撞场景。以产生0.2 s＜TTCmin≤1 s的关键危险场景的平均间隔进行比较，GA：BO：RS=1.0：5.1：17.3。结合图5和表4、表5可以看出，GA在生成关键危险场景上的效率要高于BO算法，同时二者均强于没有优化策略的RS算法。

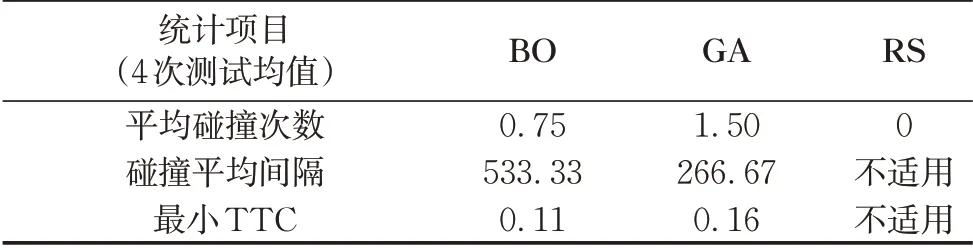
表4 不同算法生成碰撞场景效率（TTCmin≤0.2 s）Tab.4 Collision scenario generation efficiency of different algorithms(TTCmin≤0.2 s)

表5 不同算法生成关键危险场景效率（0.2 s＜TTCmin≤1 s）Tab.5 Hazardous scenario generation efficiency of different algorithms(0.2s＜TTCmin≤1 s)

图5 场景测试不同成本函数值平均频次分布Fig.5 Average frequency distribution of different cost function values of scenario testing

在搜索质量方面，本文主要关注各算法产生的关键场景的参数分散程度。由于不同优化方法采用的寻优策略存在差异性，造成场景参数分散程度有较大差别。在4次400轮迭代测试中，选取BO和GA搜索结果中成本函数值最小的37个样本，分析切入车速度、换道触发距离、换道轨迹纵向距离、前车速度4组参数中任意2组参数的分散情况，如注：对贝叶斯优化算法与遗传算法各选取了37个成本函数值最小的样本点进行离散程度分析，图中遗传算法样本点数远少于37个，是由于其多个样本点完全重叠造成。

图6所示，可以直观地看到，贝叶斯优化算法生成的场景，参数较为分散，而遗传算法的多个样本出现了不同程度的重叠。进一步以相邻具体场景参数组合欧式距离求和来量化表征参数的分散程度。结果表明，在100轮、200轮、400轮实验中，贝叶斯优化算法的该指标分别是遗传算法的28.7倍、62.2倍、31.4倍。即在搜索质量方面，贝叶斯优化算法优于遗传算法，前者搜索出的关键场景的多样性更高。图6中，对贝叶斯优化算法与遗传算法各选取了37个成本函数值最小的样本点进行离散程度分析，图中遗传算法样本点数远少于37个，是由于其多个样本点完全重叠造成。

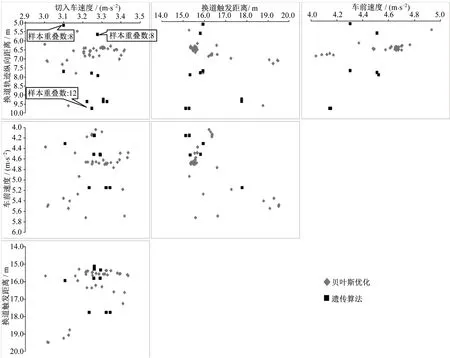
图6 不同参数组合的参数分散情况Fig.6 Parameter dispersion of different parameter combinations

针对贝叶斯优化算法和遗传算法在搜索效率和搜索质量方面的差异，本文分析认为主要原因在于二者采用的搜索策略不同。由于贝叶斯优化算法本质上采用了基于代理模型和采集函数的优化策略，遗传算法采用了基于启发式规则的优化策略，前者相比于后者更倾向于全局优化，因此在搜索质量方面表现更好，而在搜索效率和搜索速度方面表现相对较差。在实际应用中，应根据需要选择不同搜索算法，达到更好的场景生成和测试效果。

4 总结

本文面向自动驾驶决策规划系统测试过程中的关键场景测试问题，以仿真场景测试方法为基础，基于优化思想，将关键场景生成问题转化为优化搜索问题，提出了一种关键场景自动化生成方法。并以典型的前车切入场景为例，验证了本文所提方法的有效性，进一步对比了不同优化搜索算法的效果。

（1）基于优化搜索进行关键场景自动化生成，能够有效规避决策规划系统测试过程中的场景数量爆炸问题，提高发现高测试价值场景的效率，减少无意义测试场景的数量，从而提高测试效率。

（2）不同优化算法在场景生成效果上存在差异，以本文400轮迭代次数为例，这种差异较为显著。在搜索效率方面，遗传算法的搜索效率最高，随机搜索的效率最低。遗传算法和贝叶斯优化算法搜索到的关键场景数量是随机搜索算法的3.3倍和2.5倍；产生关键危险场景的平均间隔遗传算法为9.25次每危险场景，贝叶斯优化算法为47.06次每危险场景，随机搜索则为160次每危险场景。在搜索质量方面，贝叶斯优化算法优于遗传算法，以相邻具体场景参数组合欧式距离之和表征的分散程度，前者是后者的31.4倍。

（3）由于贝叶斯优化算法本质上采用了基于代理模型和采集函数的优化策略，遗传算法采用了基于启发式规则的优化策略，前者相比于后者更倾向于全局优化，因此在搜索质量方面表现更好，而在搜索效率方面表现相对较差。

综上，在实际应用场景下，结合不同的测试需求，选用合适的搜索算法，可以有效提高场景测试效率，加速测试过程。基于本文提出的方法，在后续研究中将考虑组合不同的优化算法以提高关键场景搜索效率和覆盖率，同时进一步提高算法的稳定性，以及对决策规划系统不确定性的适应能力；考虑引入离散型参数并结合自然驾驶数据等分析参数分布，构建更符合真实情况的多维复杂场景参数空间；构建成本函数时将综合考虑安全性、舒适性、鲁棒性等多维度指标，以满足不同功能和性能需求的关键场景测试。

作者贡献说明：

邢星宇：算法优化，测试结果分析，论文撰写。

吴旭阳：算法调试与仿真测试，测试结果分析，论文修订。

刘力豪：算法调试与仿真测试，论文修订。

陈君毅：研究命题提出与构思，仿真测试方案制定，论文修订。

余卓平：论文修订与审核。