基于小波优化LSTM-ARMA模型的岩土工程非线性时间序列预测

2021-09-08钱建固吴安海

同济大学学报（自然科学版） 2021年8期

钱建固，吴安海，季军，成龙，徐巍

（1.同济大学土木工程学院，上海 200092；2.同济大学岩土及地下工程教育部重点实验室，上海200092；3.上海城投水务（集团）有限公司，上海 200002；4.上海勘察设计研究院（集团）有限公司，上海 200093）

由于岩土体材料的特殊性、实际影响因素的复杂性，岩土工程应力、变形等的时间序列通常表现出十分明显的非线性特征［1］，且其演化过程具有随机性、模糊性和高度复杂性的特点。

传统的分析方法如理论分析、数值模拟和经验公式法等等［2-4］虽然具备预测的能力，但由于理论计算方法的不成熟，往往只适用于特定工况，在实际工程应用时通常存在比较大的误差，预测精度难以满足要求。

伴随着大数据科学与人工智能技术的发展，智能预测已逐渐成为岩土工程领域的发展趋势。常用的智能分析方法有：灰色预测、时间序列分析、优化算法和BP（反向传播）神经网络等［5-6］。但是这些算法都存在一些局限性。监测数据为动态数据，其随时间的推移不断更新变换，同时由于影响因素的复杂多变，还往往具有高度非线性和非平稳性的特征。而灰色预测和时间序列分析均不具备滚动预测的能力，无法以当前的预测结果为基础继续进行下一步的预测。优化算法如遗传算法、蚁群算法等则存在局部极值的问题，容易陷入局部最优点从而无法找到全局最优的预测结果。BP神经网络是一种多层前馈神经网络，层与层之间通过导数连乘来传递和更新信息，当导数很小或者很大时，BP神经网络便容易出现梯度消失和梯度爆炸的问题从而造成结果的不收敛。为了更好地分析时间序列，Hochreite和Schmidhuber［7］于1997年提出了长短时记忆神经网络（long short-term memory neural network，LSTM）。同BP神经网络相比，它不仅解决了梯度消失和梯度爆炸的问题，同时还对高度非线性的数据有着极强的映射能力，能够对岩土工程应力、变形等的时间序列做出高精度的预测。

当前智能方法在岩土工程领域中的应用大致可以分为两类。一类为基于模型的反演方法，在基本土体模型的基础上，通过对少部分数据的学习，修正基本土体模型参数，从而得到较为准确的预测结果［8］。该类方法已经较为成熟，在预测土体变形、强度等方面都得到了较为广泛的运用［9］。另一类为基于大数据的智能算法，该类方法不考虑土力学原理，直接通过相关工程数据的学习，找出不同对象间的隐藏规律，进而做出准确预测［10］。该类方法对数据的要求更高，但是技术却尚未成熟，因此在实际工程中的应用并不普及。如何改进第二类方法，使其预测结果能更好地指导生产实践便是本文的主要研究目的。

另一方面，实际工程由于受到施工、自然天气等各种随机因素的干扰，采集到的监测数据往往包含了各种噪声。噪声即高频误差，它的存在将会影响LSTM神经网络对数据的学习，最终造成预测结果的不准确。为了充分考虑噪声的影响，本文提出了基于小波优化（Wavelet Optimized）的长短时记忆神经网络-自回归滑动平均（LSTM-ARMA）预测模型。先通过小波变换提取原始监测时间序列的噪声，得到噪声项，扣除噪声项后剩余的部分即为趋势项。其中，趋势项真实反映了实际工程中应力、变形等的演化趋势，而噪声项则体现了各种随机因素的综合干扰。长短时记忆神经网络（long short-term memory network,LSTM）擅长学习阶梯性与趋势性的时间序列，自回归滑动平均模型（autoregressive moving average，ARMA）模型擅长模拟平稳时间序列（均值、方差恒定）。因此，本文分别使用LSTM神经网络和ARMA模型学习并预测趋势项和噪声项。最终将趋势项预测值和噪声项预测值之和作为总的时间序列预测值。

小波分析、LSTM神经网络与ARMA模型的结合使用在岩土工程预测分析领域比较鲜见，为了检验该组合模型的有效性与可行性，本文将其运用于上海云岭超深基坑工程的地表沉降预测中。工程实例表明，该预测方法相对误差小、预测精度稳定，具有较好的工程实用性。

1 预测模型

基于小波优化的LSTM-ARMA时序预测模型可按照以下几个步骤进行：

（1）对监测得到的非线性时间序列进行处理，剔除异常数据并且通过线性插值等方式将监测时间序列变成等距时间序列。

（2）选取适当的小波基函数和分解层数，对时间序列进行小波降噪，将其分解成趋势项和噪声项。

常用的小波基函数有db小波基（如db5、db6等）、haar小波基和sym小波基等。通过小波变换，可将原始时间序列f（t）分解成各个子信号的叠加：

其中：φj，k为近似信号；ψj，k为细节信号；cj，k与dj，k为相应的系数。近似信号与细节信号分别描述原始时间序列的低频与高频部分，但仅为相对概念，并不代表频率的绝对大小。原始信号经小波多层次分解后，每一层级上均可获得一个低频子信号与一个高频子信号［11］。

接着设置合理的阈值T，若某一时刻的子信号值低于该阈值，则认为其是由噪声产生，将其置为零从而实现去噪。常用的阈值计算方法［11］如式（2）所示：

其中：n为信号的采样长度；σ为噪声信号的方差，可根据鲁棒中值定理［11］进行计算。

最终可将原始时间序列f（t）分解成趋势项trend（t）与噪声项noise（t）之和：

（3）趋势项采用LSTM神经网络进行滚动预测。

LSTM神经网络的结构为链式结构，由一个个重复单元串联而成。重复单元的内部构造如图1所示。前已述及，BP神经网络由于结构问题，容易出现梯度消失或者梯度爆炸，从而导致结果的不收敛。而LSTM神经网络特色性地加入了细胞状态Ct用于记录长期信息、隐藏状态ht用于记录短期信息，同时设置了“门”的结构（遗忘门、输入门和输出门）用于时刻更新和丢弃信息，这使得LSTM神经网络在时间序列预测上表现优异，同时还避免了梯度消失和梯度爆炸的问题。

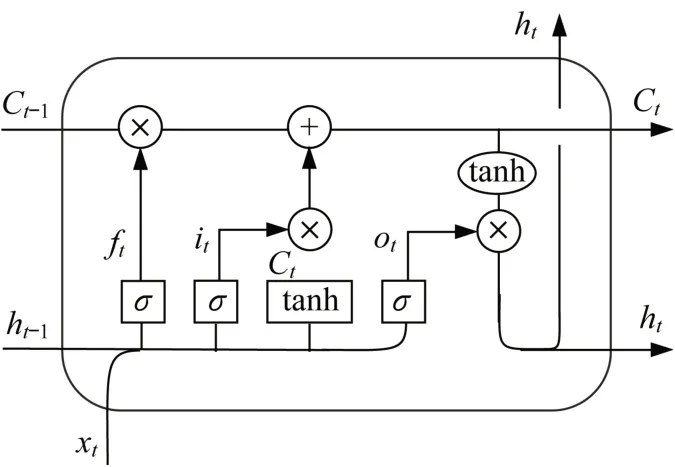
图1 LSTM重复单元示意图Fig.1 Architecture of LSTM neural network

滚动预测趋势项前，需要先构造样本用于训练LSTM神经网络。样本构造方式如表1所示，其中u代表监测变形序列中的趋势项。

表1 LSTM神经网络的输入与输出Tab.1 Input and output of LSTM neural network

m的取值从3到10不等［12］，并且可以随着可构造样本的数量进行调整，在本文中m统一取为5。后续采用滚动预测的方式进行预测，比如使用u（1），u（2），u（3），…，u（m）预测u*（m+1），然后再使用u（2），u（3），u（4），…，u（m），u*（m+1）预测u*（m+2），通过这种方式可实现多个时刻变形值的预测。

（4）噪声项采用ARMA（p，q）模型预测。

自回归移动平均模型（简称ARMA），是用来预测平稳时间序列的一种方法。令Xt为t时刻的观测值，假设Xt不仅与t时刻之前的观测值Xt-1，Xt-2，…，Xt-p有关，还与t时刻之前的扰动值εt-1，εt-2，…，εt-q相关，则Xt可写成如下形式：

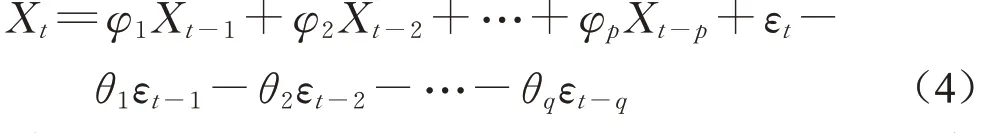
其中：φ1，φ2，…，φp与θ1，θ2，…，θq均为该线性组合的系数。

当Xt为平稳时间序列，εt为白噪声序列，且满足式（5）时，称｛Xt｝为p阶自回归与q阶滑动平均混合序列，记为ARMA（p，q）。

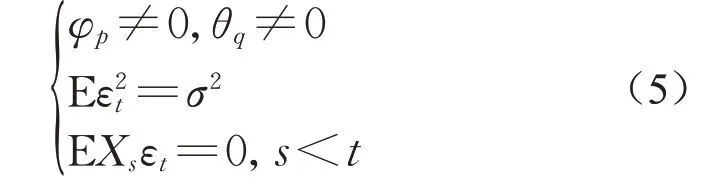
其中：E表示的是数学期望。ARMA模型的使用前提是序列的平稳性。因此，首先要使用增广迪基-富勒检验（augmented Dickey-Fuller test，ADF）单位根判别噪声序列是否平稳，若平稳，则可采用ARMA模型进行预测，否则需要调整小波基函数和分解层数，直至噪声序列为平稳时间序列。

随后需计算不同p、q组合下该噪声序列的信息准则值，如常用的赤池信息准则（akaike information criterion，AIC）与贝叶斯信息准则（Bayesian information criterion，BIC）等，用以评估拟合模型优劣的衡量标准，进而实现对模型中的变量起到优化选择［13］。信息准则值越小则表示相应（p、q）阶的ARMA模型越好。

（5）将趋势项预测值与噪声项预测值相加得到总的时间序列预测值yi（i=1，2，…，n），并与监测值fi对比，分析误差情况。常用的误差评价指标有均方根误差（RMSE）与平均百分比误差（MAPE）：

式中：RMAPE为均方根误差；RRMSE为平均百分比误差。

预测流程如图2所示。预测前后趋势项与噪声项的曲线示意图如图3所示。趋势项与噪声项求和便可得到总的时间序列。

图2 预测流程图Fig.2 Flowchart of the forecast model

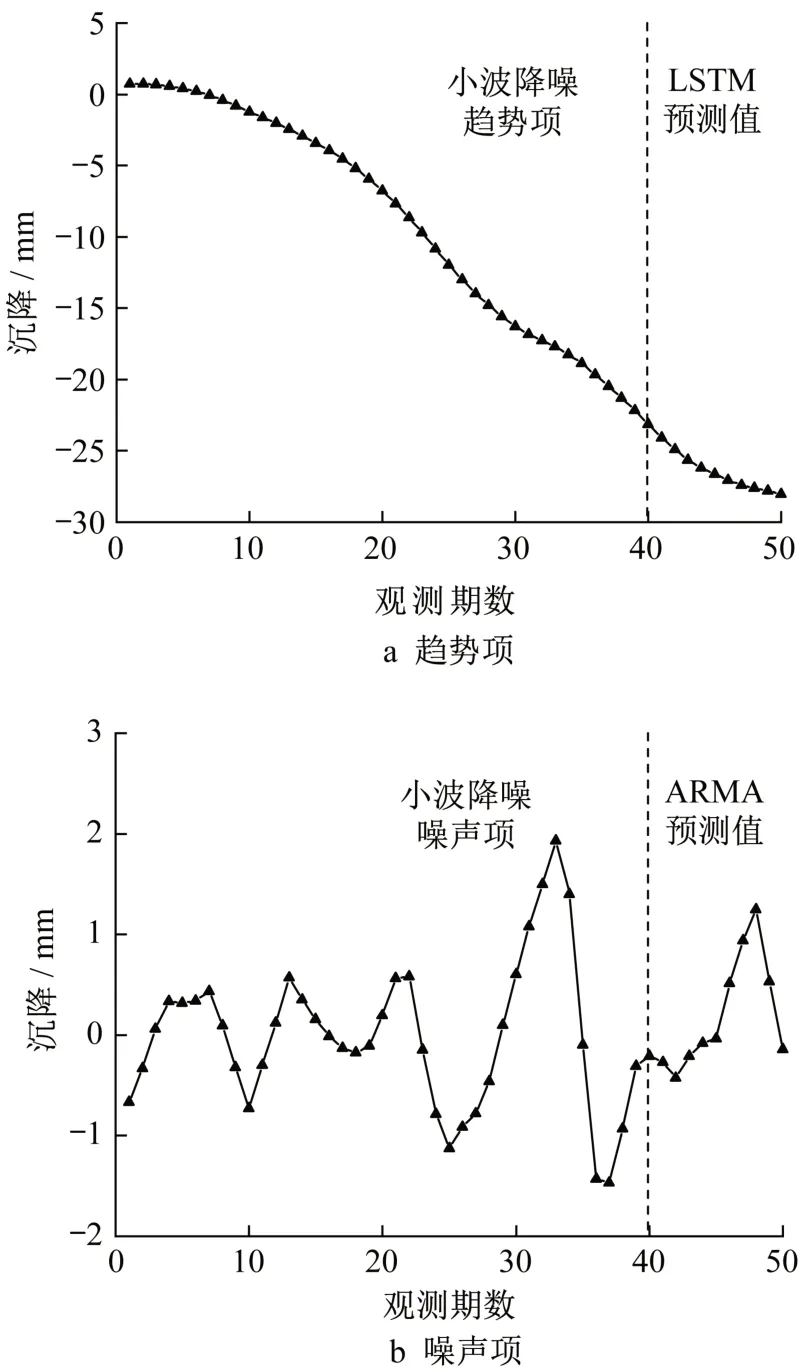
图3 预测前后趋势项与噪声项的曲线示意图Fig.3 Curves of trend term and noise term before and after prediction

2 工程实例分析

2.1 工程概况

云岭基础设施基坑为上海苏州河段深层排水调蓄管道系统工程的一部分。基坑呈圆形，直径34 m，目标深度57.84 m，超过国内基坑最大开挖深度51 m。支护结构采用1 500 mm连续墙，地连墙采用铣接头，逆作内衬墙。基坑地处上海软土区域，地质条件复杂，且深层土体力学特性不明，因此周边布置了大量监测点。基坑外地表沉降测线布设和基坑剖面分别如图4、图5所示。

图4 超深基坑平面及地表沉降测线布置Fig.4 Plan and monitoring arrangement of the ultradeep foundation pit

图5 超深基坑剖面图（单位：m）Fig.5 Profile of ultra-deep foundation pit（unit:m)

基坑周围布设了4条沉降测线，分别为DB1、DB2、DB3和DB4，其与图4水平方向的夹角依次为11.6°、86.2°、8.3°和87.2°。本文选取每条测线上的第一个监测点（即DB1-1、DB2-1、DB3-1、DB4-1）的沉降监测数据用于训练和检验该预测模型。这4个监测点与竖井间的距离均约为4.8 m。

需指出的是，目前基坑开挖尚未完工，以下选取了自开工2017.11.6至最近2020.8.24期间共计10个工况，记为工况1～工况10，具体情况如表2所示。其中，测点DB4-1在工况8中由于施工原因被毁，相应的监测数据只更新至2020.6.7为止。

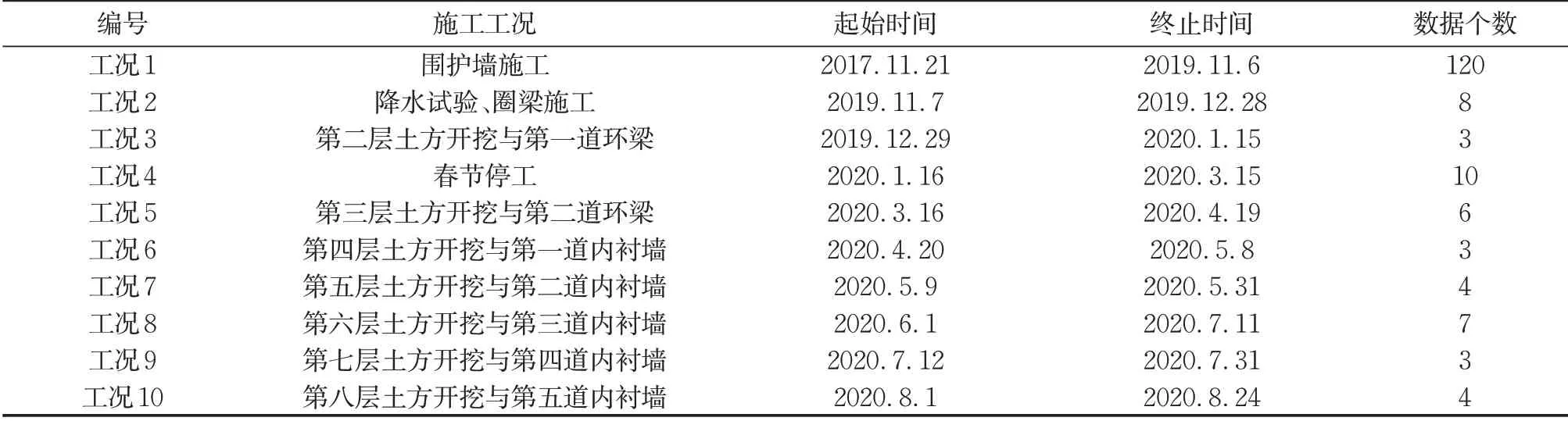
表2 施工工况Tab.2 Construction conditions

2.2 数据预处理

现场采集的监测数据并非等时间间隔，需要进行插值处理。为了减少插值的影响，维持原始时间序列的变化规律，本文选用分段线性插值的方法。插值起始时间为2017.11.21，间距为6 d。插值后的沉降监测点DB1-1、DB2-1、DB3-1和DB4-1的数据如图6所示，从左到右依次为工况1～工况10，分别对应120、8、3、10、6、3、4、7、3、4组数据，如表2所示。

图6 地表沉降时程曲线Fig.6 Ground surface deformation

2.3 DB1-1监测数据建模预测

现以DB1-1沉降监测数据为例，详细描述如何建立LSTM-ARMA时序预测模型。

首先利用工况1的监测数据建模预测工况2的沉降变形，接着利用工况1和工况2的监测数据建模预测工况3的沉降变形，依此类推，最后利用工况1～工况10的监测数据建模预测未来工况的沉降变形。

2.3.1 工况2沉降变形的预测

（1）小波降噪分析

实际工程由于受到各种因素的干扰，所采集的监测数据将会包含一定的噪声，需要对其进行小波降噪从而获得真实的历史沉降信息。去噪步骤为：首先，分别选用小波基函数db10、db15和db20对工况1的监测数据依次进行3层、4层和5层的小波分解；提取出高频噪声后分别计算信噪比SNR和均方根误差RMSE，信噪比越大、均方根误差越小则代表分解效果越好［14］。计算结果如表3所示。

表3 小波降噪结果对比Tab.3 Comparison of different wavelet denoises

在小波基函数为db20且分解层数为3的情况下，信噪比为23.802 5，均方根误差为0.550 3，去噪效果最为理想。此时，提取的趋势项与噪声项如图7所示。

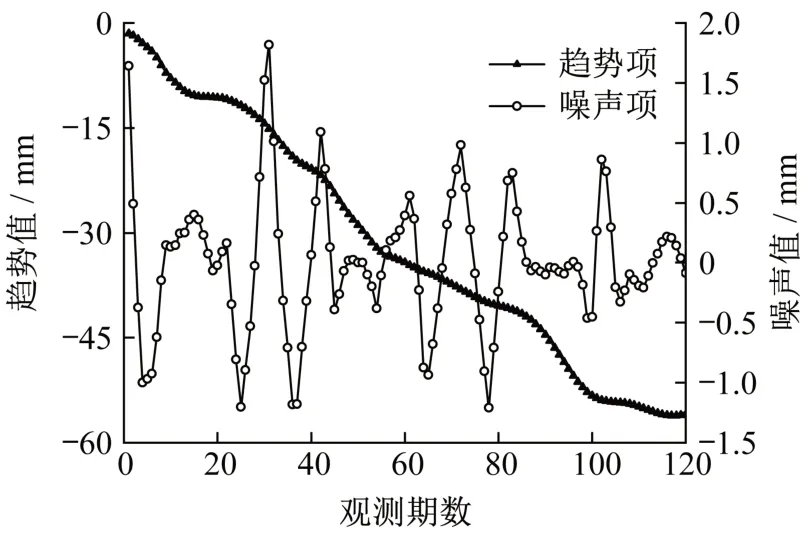
图7 DB1-1工况1的趋势项与噪声项Fig.7 Trend and noise term of DB1-1 in working condition 1

（2）趋势项预测

趋势项采用LSTM网络进行预测，样本构造采用“5+1”模式，即采用当前时刻以及前4个时刻的值不断滚动预测下一时刻的值。

（3）噪声项预测

噪声项采用ARMA模型进行预测。图7表明噪声曲线直观上为平稳时间序列，需要经过ADF单位根进行进一步的平稳性检验。经过计算，ADF值为-7.343 3，由表4可知，该噪声序列在99%的置信概率下为平稳时间序列，因此可使用ARMA模型。

表4 不同置信区间对应的临界ADF值Tab.4 Critical ADF values corresponding to different confidence intervals

根据AIC准则［13］绘制噪声序列的热力图，如图8所示。图中，信息准则值与热力图颜色深浅的对应关系参照图右方的色带。当p（即AR系数）取2、q（即MA系数）取5时，图中小矩形的颜色最深，表示此时的信息准则值最小、模型最优。

图8 噪声项热力图Fig.8 Thermograph of noise term

（4）总的变形预测

将趋势项的预测结果和噪声项的预测结果之和作为总的预测值，如图9所示。为了证明该组合模型的优越性，在不采用小波降噪与ARMA模型的前提下，直接使用LSTM模型预测工况2的沉降变形，结果如图10所示。

2.3.2 后续工况沉降变形的预测

按照同样的方法，分别利用工况1～2、1～3、1～4、1～5、1～6、1～7、1～8、1～9与1～10的监测数据建模预测工况3、4、5、6、7、8、9、10与未来工况的沉降变形，结果如图9所示。同时，也只使用LSTM模型对后续工况进行了预测，预测结果如图10所示。

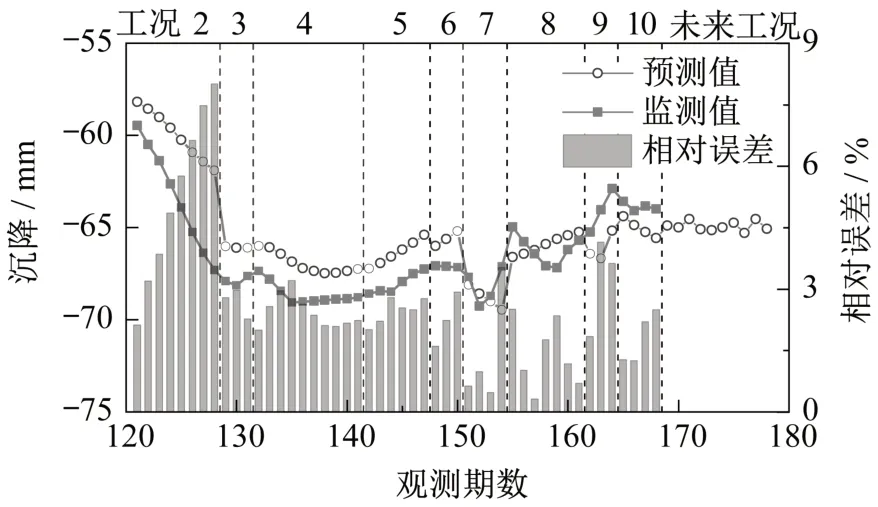
图9 DB1-1工况2～工况10的LSTM-ARMA预测结果Fig.9 LSTM-ARMA prediction results of DB1-1 in working conditions 2-10

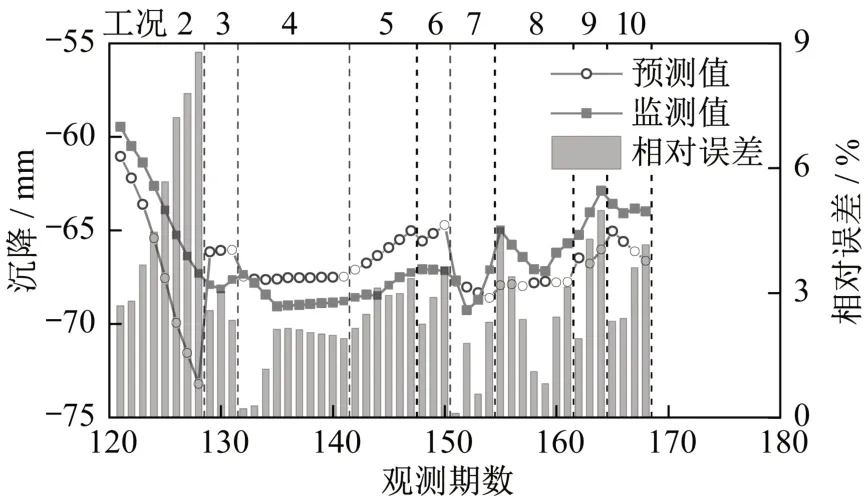
图10 DB1-1工况2～工况10的LSTM预测结果Fig.10 LSTM prediction results of DB1-1 in working conditions 2-10

图9 表明，工况2的预测精度最差，最大相对误差高达8.00%，而其余工况的最大相对误差均不超过4.20%。这主要是由于工况2为抽水试验和疏干降水，其引起监测点变形的速率要大于工况1中的围护墙施工，而工况2的预测采用的是工况1的变形数据进行建模，LSTM网络所学习的变形规律均为工况1监测点的变形规律，所以不能很好地预测工况2的沉降变形。相比之下，工况3～工况10阶段产生的变形较小，预测也更加准确。

图9说明，当使用基于小波优化的LSTMARMA模型时，相对误差在0.30%～8.00%之间，平均值为2.66%，方差为2.64。而根据图10，只使用LSTM模型进行预测时，相对误差在0.09%～8.78%之间，平均值为2.89%，方差为3.16。虽然在少部分期数中（如第122期、第123期等），后者的预测误差稍低，但从整体上看，前者的预测误差在平均值和方差上都比后者更小，因此LSTM-ARMA模型的预测效果更加理想。

2.4 其余监测点监测数据的建模预测

基于同样的方法和步骤，对插值后DB2-1、DB3-1和DB4-1的沉降数据进行建模预测，结果如图11、图12和图13所示。

图11 DB2-1工况2～工况10的LSTM-ARMA预测结果Fig.11 LSTM-ARMA prediction results of DB2-1 in working conditions 2-10

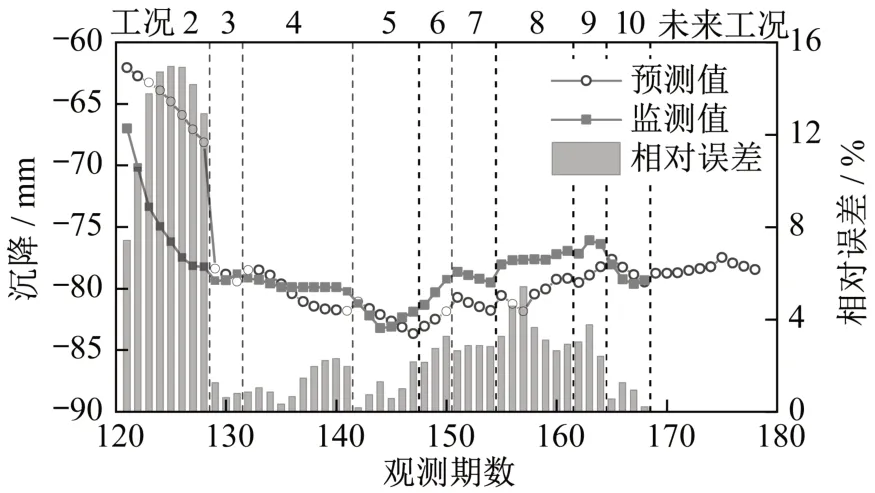
图12 DB3-1工况2～工况10的LSTM-ARMA预测结果Fig.12 LSTM-ARMA prediction results of DB3-1 in working conditions 2-10

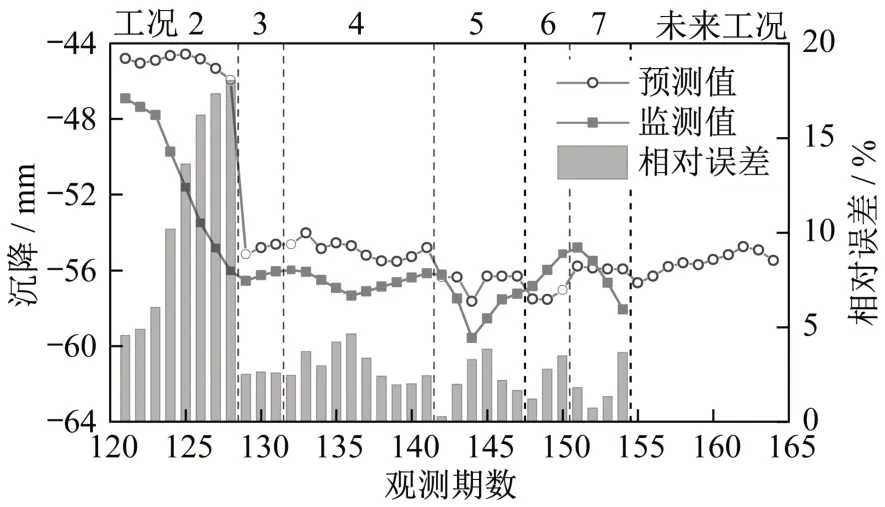
图13 DB4-1工况2～工况7的LSTM-ARMA预测结果Fig.13 LSTM-ARMA prediction results of DB4-1 in working conditions 2-7

显然，4个监测点的沉降规律基本一致，且工况2的预测误差都比较大，最大相对误差超过18%；而工况3～工况10的预测误差均比较小，最大相对误差不超过6%。这与监测点在工况1和工况2下的变形速率相差过大有关。

此外，利用LSTM-ARMA模型预测DB2-1、DB3-1和DB4-1的平均相对误差分别为2.91%、3.80%和4.61%，方差分别为12.91、19.39和22.21。而只采用LSTM模型预测的平均相对误差为4.35%、6.14%和4.18%，方差为20.17、42.73和16.95。综合来看，LSTM-ARMA模型取得了更好的预测结果。

2.5 样本数量的影响

样本数量对于LSTM正确学习序列规律具有较大的影响，样本数量若过少，LSTM则难收敛，甚至得不到最优解，为此，以下将探讨样本数量对LSTM-ARMA模型预测精度的影响。以测点DB1-1为示例，分别用最新30期、60期、90期和120期工况1的沉降监测数据训练ARMA-LSTM模型，并使用训练完毕的模型预测工况2的沉降值。预测误差结果如图14所示。

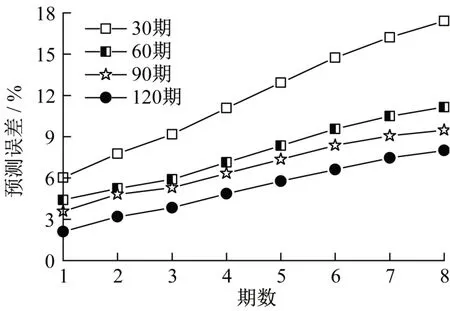
图14 不同样本数量下的模型预测误差对比Fig.14 Comparison of prediction errors in different sample quantities

不难看出，样本数量的增加能提高模型的预测精度。当样本数量为30，即仅使用工况1最新30期数据预测工况2沉降值时，最大预测误差高达18%；而当样本数量增加至60时，最大误差减小一半，约为9%；此后继续增加样本数量，预测精度可以进一步提高，但是提高幅度减小。由此可见，依据预测精度要求，有必要合理地选择样本数量；在满足工程需求的条件下，继续增大样本数量，对提高预测精度非常有限，反之还将显著降低计算效率。

3 有限元验证

为了说明LSTM-ARMA智能预测模型的有效性，这里将地表总沉降分成两部分，即基坑开挖诱发沉降与非开挖诱发沉降，其中，基坑开挖诱发的地表沉降采用弹塑性有限元预测，而非开挖因素（降水、围护墙施工、地表堆载等）诱发的沉降变形则仍采用智能预测模型预测，二者叠加之后便与现场实测的真实变形作对比验证，计算剖面为DB1-1。

有限元数值模型如图15所示，考虑圆形基坑的轴对称性，建立轴对称准三维模型。土层剖面按图5确定，土体模型采用适用于软土应力应变响应的HS（Hardening-Soil）模型［15］，参数如表5所示，取值参考文献［16］。有限元模型的结构参数如表6所示，其中包括地连墙、围檩与内衬墙，当土体开挖至指定深度时，便将围檩与内衬墙相应范围内的刚度附加至地连墙中，以模拟围檩与内衬墙的施工。以DB1-1工况1的沉降监测序列预测工况2～工况10的沉降变形为例，该过程具体如下所示。

表6 有限元模型结构参数Tab.6 Structure parameters of finite element model

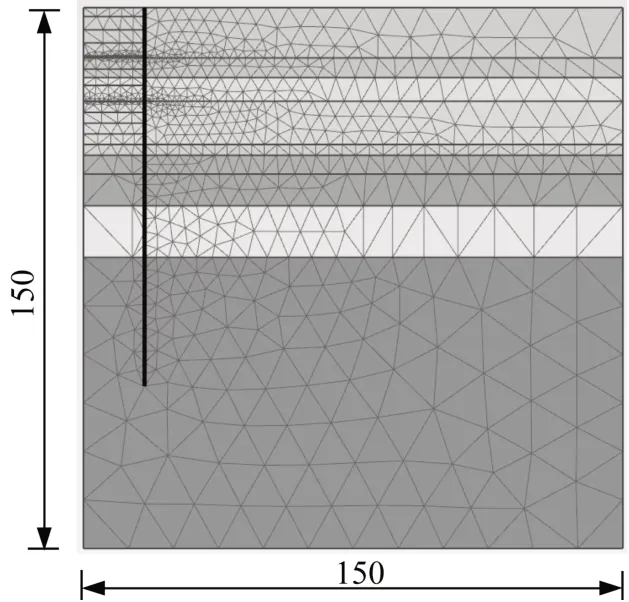
图15 有限元模型网格划分（单位：m）Fig.15 Mesh generation of finite element model（unit:m)

表5 有限元模型土体参数Tab.5 Soil parameters of finite element model

整个基坑开挖全过程对应于表2中的工况2～工况10，预测的最大开挖深度35 m，考虑软土地层渗透性小，且施工期相对较短，数值分析忽略开挖期间的排水固结效应。开挖有限元预测、非开挖人工智能模型预测及二者叠加如图16所示，对比实测结果可以看出，不仅二者的发展趋势上吻合较好，同时在数量上也较为接近，其最大相对误差不超过9%，平均相对误差也仅为5%左右。值得一提的是，开挖初期采用有限元预测与人工智能预测的叠加结果，要好于单一的人工智能模型预测，而随着后期工况的发展，两类预测结果差异性逐渐减小，表明单一的人工智能预测在工况突变阶段（对应于本案例为非开挖到开挖过渡阶段），可能引起较大的约误差。