短焊钉布置对超高性能混凝土组合桥面板抗弯性能影响

徐 晨，张乐朋，江 震，马 骉

（1.同济大学土木工程学院，上海 200092；2.上海市政工程设计研究总院（集团）有限公司，上海 200092）

超高性能混凝土（ultra-high performance concrete，UHPC）与正交异性钢桥面板通过连接件结合可显著提高钢桥面板刚度、降低钢结构疲劳开裂风险以及减缓铺装层结构病害［1-3］。UHPC立方体抗压强度一般为120～150 MPa，单轴抗拉强度可达7 MPa以上，且具优良的大应变拉伸硬化特征［4］。

钢-UHPC组合桥面板中连接件是保证结构组合效应的关键，主要形式包括焊钉、型钢以及短钢筋网等，焊钉是其中的常用连接件。钢-UHPC组合桥面板中UHPC板厚小，焊钉长仅40 mm左右，直径为13 mm，长径比约为3，这与常规组合梁中的焊钉长径比不同。另一方面，钢-UHPC组合桥面板主要为刚度及疲劳控制设计，焊钉间距一般较大，截面应变分布具有明显的不连续特性，呈显著的部分组合特征，这与常规组合梁中的焊钉布置有较大的不同。可见组合梁中焊钉抗剪设计方法并不完全适用于钢-UHPC组合桥面板中的短焊钉连接件。近年来，钢-UHPC组合桥面板在新建桥梁与改造旧桥项目中的应用正迅速增加［5］，焊钉连接件的合理布置是影响结构安全及经济性的关键。

针对钢-UHPC组合桥面板中短焊钉连接件的研究主要是考察连接件自身的静力与疲劳特性［6-8］，而焊钉布置间距对组合桥面板组合效应的影响规律并不明确，钢-UHPC组合桥面板刚度计算理论并不完善，这对该类构件的应用推广以及包含该类构件的受力可靠性造成影响。李文光等［9］对钢-UHPC组合简支板进行了静力受弯试验研究，发现正弯矩作用下其破坏形态为板端焊钉被剪断，而后通过理论分析推测加密焊钉布置可提高组合板的承载力与延性；Luo等［10］通过对钢-UHPC组合板进行静力受弯试验以研究组合桥面板横桥向开裂特性，试验结果表明焊钉间距由150 mm增大为200 mm会导致UHPC开裂荷载降低并促进裂缝发展。这些研究均表明焊钉间距的确对组合桥面板的抗弯性能具有影响。

综上所述，焊钉间距对钢-UHPC组合桥面板组合效应、结构刚度、UHPC开裂特性等的影响规律并未明确，这些均为建立成熟组合桥面板设计理论的重要基础。本文依托某工程对钢-UHPC组合桥面板中短焊钉的合理布设展开研究，通过足尺节段桥面板在两种工况下的弯曲荷载试验以及基于材料弹塑性损伤模型的有限元参数化分析考察了短焊钉间距对结构组合效应、抗弯刚度、负弯矩区UHPC开裂特性以及焊钉受剪作用等的影响规律，为焊钉间距合理化设计提供理论基础。

1 试验设计

1.1 试件设计

本文设计制作了2个带球扁钢加劲肋的足尺节段钢-UHPC组合桥面板试件。如图1所示，试件长7 000 mm、宽1 960 mm、高488 mm；加劲肋高180 mm，厚11 mm，间距400 mm；横肋间距2 000 mm。UHPC板厚与钢盖板厚分别为60与12 mm；UHPC板内纵横向钢筋直径16 mm，间距100 mm，保护层厚度15 mm。试件中焊钉直径和高度分别为13和40 mm。两个试件的焊钉间距分别为200 mm×200 mm与300 mm×300 mm，试件编号分别为D200和D300。UHPC浇筑完成后在夏季室外环境覆膜养护，环境温度约为20℃～30℃。

图1 试件构造示意图（单位：mm）Fig.1 Schematic diagram of specimens(unit:mm)

1.2 材性试验

表1所列为UHPC分别养护7与28 d按标准试验方法［11］测得的材料基本力学性能，材性试件与桥面板试件在同场地养护。通过对一组3个哑铃型试件（中间段截面尺寸50 mm×100 mm）进行轴拉试验，测得UHPC的平均拉伸应力-应变曲线，如图2所示，曲线峰值点对应极限抗拉强度与极限抗拉应变。所用UHPC的钢纤维体积掺量为2.3%。按照标准试验方法［12］测得钢板与钢筋的材性试验结果：16 mm直径钢筋屈服强度与极限强度分别为480与689 MPa；11 mm厚与12 mm厚钢板屈服强度分别为455与411 MPa，极限强度分别为607与547 MPa。

图2 28 d龄期UHPC轴拉应力-应变曲线Fig.2 Uniaxial tensile stress-strain curve of 28-dayold UHPC

表1 UHPC材性试验结果Tab.1 Material property test results of UHPC

1.3 加载方案

本试验包含2种加载工况。工况1为4道横肋连续支承的两跨跨中同步加载工况（图3），主要考察试件在连续支承情况下焊钉间距对挠度发展、负弯矩区UHPC开裂特性等的影响规律；工况1加载时，在4#支承处配置40 kN压重以防脱空。分级单调加载至负弯矩区UHPC最大裂缝宽度达0.10 mm时，即停止加载并卸载作动器至0。随后撤去2#、3#支承与作动器1，转换进入两端简支跨中加载工况（以下简称工况2）。工况2主要考察焊钉间距对组合桥面板正弯极限状态的影响规律。试验中监测了关键截面挠度、各构件应变、UHPC裂缝宽度等数据。

图3 工况1加载示意图（单位：mm）Fig.3 Loading diagram of Condition 1(unit:mm)

2 试验结果与分析

2.1 荷载-挠度曲线

图4a所示为工况1下试件中跨的荷载-挠度曲线。挠度为跨中2-2截面处（图3）挠度计的平均结果。在工况1下，两个试件初开裂均发生在中支点1-1截面处（图3），随荷载增加裂缝沿桥面板横向发展。可见两个试件的荷载-挠度曲线近似直线且基本重合，表明试件保持在弹性状态，焊钉间距分别为200 mm与300 mm对连续支承下组合桥面板抗弯刚度影响并不明显。

图4b所示为工况2下试件的荷载-跨中挠度曲线。曲线包含弹性阶段，塑性发展阶段和失效阶段。在塑性发展阶段，跨中纵肋底缘受拉屈服，产生塑性变形；在失效阶段，跨中纵肋塑性变形快速发展，跨中UHPC顶部压溃。图5所示为试件D200在工况2下的极限状态，两个试件极限状态相似。定义每延米截面正弯弹性极限弯矩为工况2下跨中2-2截面纵肋底缘应变达2004×10-6（材性试验所得11 mm厚钢板屈服应变）时，横桥向每延米截面所承受的弯矩。试件D200与试件D300该值分别为194.9与187.8 kN·m，试件D300较试件D200降低了3.7%。定义每延米截面正弯承载能力极限弯矩为工况2下跨中荷载达到最大值时，横桥向每延米跨中2-2截面所承受的弯矩。试件D200与试件D300该值分别为359.7与342.8 kN·m，为各自正弯弹性极限弯矩的1.8～1.9倍，表明试件在纵肋底缘受拉屈服后仍有较高的安全储备。

图4 试件荷载-挠度曲线Fig.4 Load-deflection curves of specimens

图5 试件D200极限状态（工况2）Fig.5 Ultimate status of specimen D200(Condition 2)

2.2 负弯矩区UHPC开裂特性

工况1下，试件D200和试件D300首次观察到0.05 mm宽裂缝的荷载等级分别为400与450 kN，试件D300的荷载较试件D200提升了12.5%。试件D200和试件D300分别于单个作动器为850与900 kN时最大裂缝宽度达0.10 mm，图6所示为两个试件该状态时的裂缝分布图。可见试件D200中的裂缝长度较试件D300更长，开裂更为明显，图中虚线箭头指向裂缝宽0.10 mm位置处。考虑到主梁体系对组合桥面板受力的不利影响，保守定义每延米截面负弯弹性极限弯矩为工况1下中支点1-1截面UHPC裂缝宽达0.10 mm时，横桥向每延米截面所承受的弯矩。试件D200与试件D300该值分别为152.0与160.7 kN·m，试件D300较试件D200提高了5.7%。该状态下两个试件UHPC板受拉边缘纵向应变最大值的平均结果为1 878×10-6，约占材料极限拉应变的59%。图7所示为工况1下中支点1-1截面处UHPC板受拉边缘纵向应变发展曲线，应变值取未受开裂影响测点的平均结果。可见试件D200更早达到初裂应变。

图6 负弯矩区UHPC裂缝分布（工况1）（单位：mm）Fig.6 Distribution of UHPC cracks at negative moment area(Condition 1)（unit：mm）

图7 1-1截面UHPC受拉边缘纵向应变发展（工况1）Fig.7 Development of longitudinal strain at UHPC tensile edge at cross-section 1-1(condition 1)

以上现象表明，焊钉间距由200 mm增大至300 mm对连续支承组合桥面板负弯矩区UHPC抗裂性能更为有利。

2.3 截面弯矩使用率分析

基于结构力学最不利内力计算方法并按照规范［13］计算得到在试验试件上布置单车道的车辆荷载作用下，跨中2-2截面与中支点1-1截面所产生的最大每延米截面正、负弯矩值分别为15.8与19.3 kN·m。根据2.1节与2.2节中得到的每延米截面正、负弯弹性极限弯矩可得到在仅考虑单车道车辆荷载作用情况下的试件截面弯矩使用率。计算结果表明，试件D200的中支点1-1截面与跨中2-2截面弯矩使用率分别为12.7%与8.1%；试件D300中对应两处截面弯矩使用率分别为12.0%与8.4%。中支点1-1截面弯矩使用率平均高于跨中2-2截面近50%，表明连续支承组合桥面板中，中支点截面更易成为控制设计截面。

3 钢-UHPC组合桥面板静载试验有限元模拟

本节建立了考虑材料弹塑性损伤的实体板壳有限元模型对试验过程进行模拟。将计算结果与试验结果对比以检验模拟可靠性。

3.1 有限元模型与材料本构

采用ABAQUS建立有限元模型，UHPC板、钢筋、钢结构、焊钉分别采用C3D8R单元、T 3D2单元、S4R单元、Connector单元模拟。模型编号为DS200与DS300，分别对应试件D200与试件D300。

UHPC受拉本构曲线如图2所示。受压本构关系以文献［14］中提出的拟合公式计算。棱柱体抗压强度与初始弹性模量按28 d龄期的材性试验结果设置，受压峰值点应变取2 550×10-6，试验拟合参数根据文献［15］中研究结果取2.0。模型中引入混凝土塑性损伤模型以模拟UHPC受拉开裂特征。按式（1）在应力-应变曲线的基础上推导应力-非弹性应变曲线，按式（2）推导损伤因子-非弹性应变曲线［16］。

式中：εin为非弹性应变；E为初始弹性模量；d为损伤因子；εpl为塑性应变，文献［16］中假定εpl=βεin，β根据文献［17］中研究结果取0.7。

UHPC其他材性参数参照文献［18］设置。钢板、钢筋本构关系采用基于材性试验结果的双折线弹塑性模型，泊松比与弹性模量分别设置为0.3与210 GPa。焊钉剪切刚度采用基于同型号焊钉推出试验结果的非线性模型定义［19］。此外，模型的支承与加载条件与试验试件一致，在UHPC顶面选取试验中分配梁作用区域设置面荷载（工况1）与位移荷载（工况2）以模拟试验加载。

3.2 有限元模拟结果验证

图8a所示为工况1下计算与实测所得荷载-跨中挠度曲线，图8b与图8c分别所示两个模型在工况2下的荷载-挠度曲线对比，可见计算结果与实测结果吻合较好，验证了有限元模拟方法的准确性。

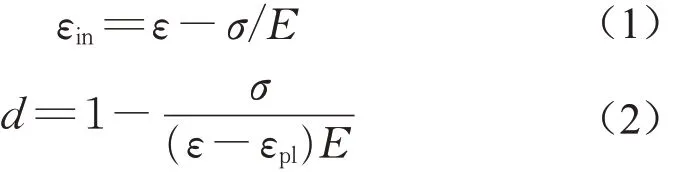
图8 荷载-挠度曲线对比Fig.8 Comparison of load-deflections

4 钢-UHPC组合桥面板短焊钉间距参数化分析

基于得到验证的有限元模型，展开焊钉间距参数化分析。参考规范［20］，参数化分析中焊钉间距取值范围为100～400 mm，按50 mm等间隔取值，焊钉横纵向间距相等。各模型以“DS+焊钉间距”编号。

4.1 荷载-挠度曲线

图9所示为工况1下部分模型的荷载-跨中挠度曲线。可见焊钉间距增大导致模型抗弯刚度出现退化。以曲线上250 kN对应点的割线斜率作比较，相比于DS100，DS200、DS300、DS400的刚度分别退化了8.6%、12.5%，14.1%。这对控制组合桥面板局部下挠是不利的。

图9 有限元模型荷载-挠度曲线（工况1）Fig.9 Load-deflection curves of FE models(Condition 1)

表2所列为工况2下由各模型计算得到的跨中2-2截面每延米正弯弹性极限弯矩和相比于DS100的增长率。可见焊钉间距增大导致每延米截面正弯弹性极限弯矩降低。相比于DS100，DS400每延米截面正弯弹性极限弯矩降低比例仅为8.3%。

表2 跨中2-2截面每延米正弯弹性极限弯矩汇总（工况2）Tab.2 Summary of positive elastic limit bending moment of mid-span per meter section 2-2(Condition 2)

4.2 组合桥面板截面应变分布

图10 所示为工况1下部分模型在单个跨中荷载达250 kN时结构纵向应变沿中支点1-1截面高度分布，此时模型中UHPC尚未开裂。可见UHPC板与正交异性钢板交界面处存在显著的应变突变，表明模型处于部分组合状态。随焊钉间距增大，交界面处应变不连续差值逐渐增大（差值标注于图中交界面处）。相比于DS100，DS400该值增大了60.3%。表明钢-UHPC组合效应随焊钉间距增大逐渐减弱。

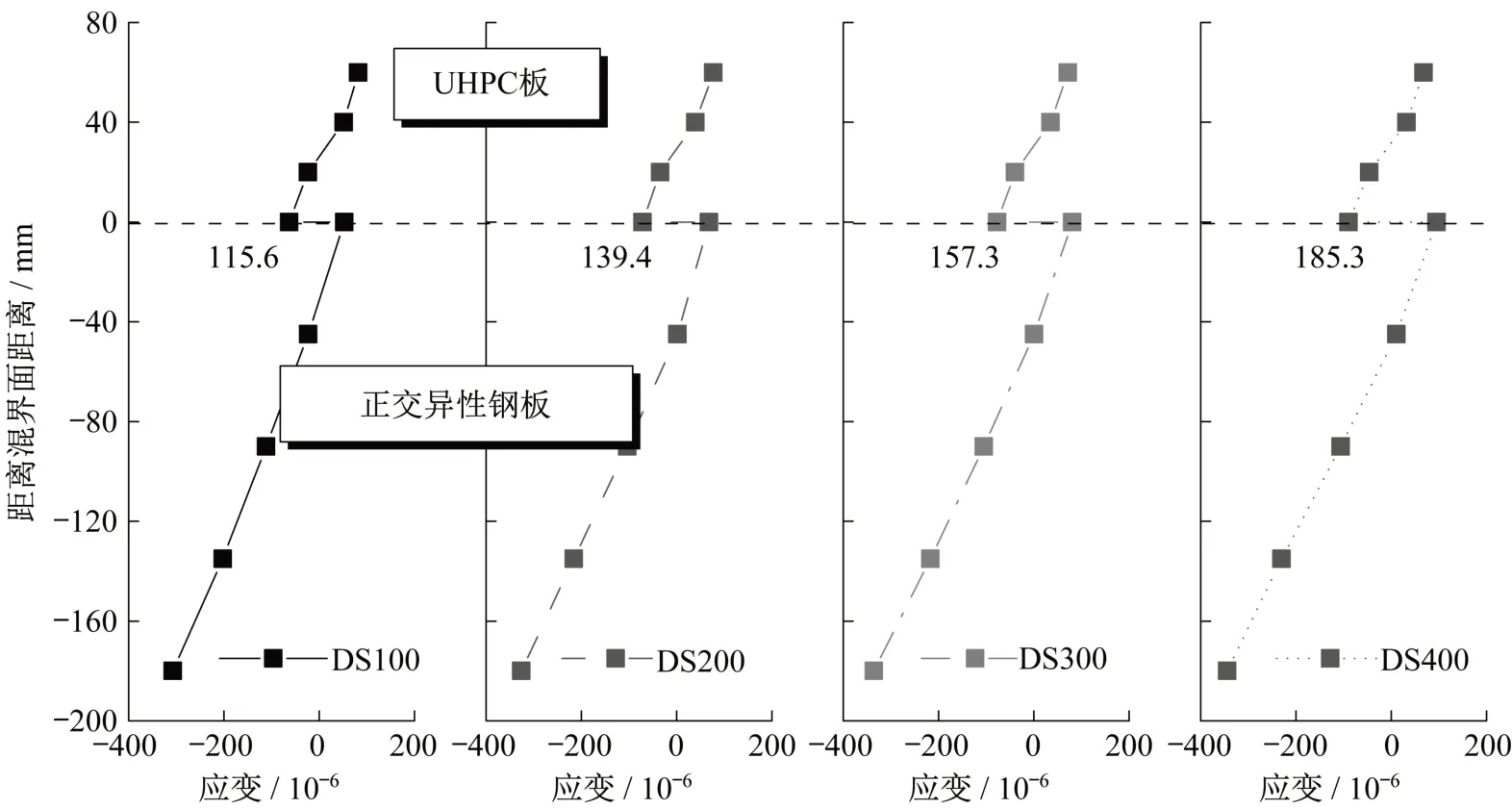
图10 纵向应变沿1-1截面高度分布Fig.10 Distribution of longitudinal strain along section height 1-1

4.3 负弯矩区UHPC受力状态与钢筋应力发展

图11为工况1下部分模型中支点1-1截面UHPC受拉边缘主拉应力平均值的发展曲线。表3列出由各模型得到的开裂荷载和相比于DS100的增长率。开裂荷载定义为模型中主拉应力平均值超过UHPC 28 d初裂抗拉强度（8.5 MPa）时对应荷载。DS200与DS300的开裂荷载与试验中裂缝宽达0.05 mm时对应试件荷载等级基本吻合。由表3可知，开裂荷载等级随焊钉间距增大而显著提升。相比于DS100，DS400的开裂荷载等级提升了84.2%。

图11 中支点1-1截面UHPC平均主拉应力发展Fig.11 Development of UHPC average max principal stress at support cross-section 1-1

表3同时列出中支点1-1截面每延米的负弯弹性极限弯矩。由于模型中无法直接得到裂缝宽度，以受拉损伤因子代为表征。DS200与DS300在850与900 kN时（对应试件UHPC裂缝宽达0.10 mm时荷载等级）1-1截面UHPC平均受拉损伤因子分别为0.486与0.494，故取平均值0.490表征UHPC开裂宽度达0.10 mm。由表3可知，焊钉间距增大导致1-1截面每延米负弯弹性极限弯矩显著增长。相比于DS100，DS400该值增长率达67.8%。

图12 所示为工况1下部分模型中支点1-1截面处钢筋平均纵向应力发展曲线。各模型钢筋均呈现出裂后拉伸硬化现象。随焊钉间距减小，钢筋纵向应力的增加速率显著增大，在UHPC开裂后尤为明显。另一方面，随焊钉间距增大，钢筋纵向应力值减小。这是由于模型中纵向钢筋布置于UHPC板厚中间位置，焊钉间距增大带来的组合效应减弱使得UHPC板呈现出独立受弯的趋势。

?

图12 1-1截面钢筋纵向应力发展Fig.12 Development of longitudinal stress of reinforcements at cross-section 1-1

4.4 焊钉受剪作用水平

在模型中设置多个工况模拟不同位置处的单车道车辆荷载［13］与疲劳荷载计算模型Ⅲ［20］，分别得到焊钉所承受的最大剪力与最大剪应力幅。计算结果表明，随焊钉间距增大，单个焊钉所承受的最大剪力与最大剪应力幅提高。根据规范［20］计算得到试件中焊钉的抗剪承载力为25.5 kN，大于DS400中最大焊钉剪力18.7 kN，但DS400中焊钉的最大等效剪应力幅超过规范［20］中的限值（90 MPa）19%，DS350中焊钉的最大等效剪应力幅为88.2 MPa，已十分接近限值。

4.5 截面弯矩使用率对比

以表2与表3中所列跨中2-2截面与中支点1-1截面的每延米截面弹性极限弯矩与2.3节中计算得到的单车道车辆荷载作用下的每延米截面弯矩，计算各模型1-1、2-2截面弯矩使用率（图13）。可见随焊钉间距增大，中支点1-1截面的弯矩使用率明显降低，同时，跨中2-2截面的弯矩使用率提高并不明显，两处截面的弯矩使用率逐渐接近相等，提示结构受力趋向于更为经济。

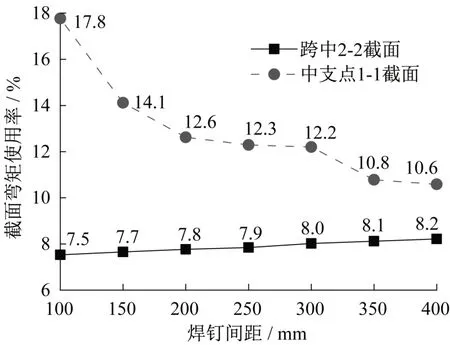
图13 截面弯矩使用率对比Fig.13 Comparison of utilization rate of section bending moment

5 结论

本文通过对2个焊钉间距分别为200 mm和300 mm的足尺节段钢-UHPC组合桥面板试件进行弯曲荷载试验以及考虑材料弹塑性损伤的有限元参数化分析，考察了长径比小于4的短焊钉间距对钢-UHPC组合桥面板抗弯性能的影响规律，结论总结如下：

（1）根据连续支承两跨跨中加载试验结果，相比于焊钉间距200 mm的部分组合桥面板，焊钉间距增大为300 mm时，桥面板负弯矩区UHPC开裂达0.05 mm宽时对应荷载等级提升了12.5%，开裂达0.10 mm宽时UHPC板裂缝长度较短，此时UHPC拉应变平均值为1 878×10-6，约占材料极限拉应变的59%。

（2）根据简支跨中加载试验结果，焊钉间距从200 mm增大为300 mm时，跨中截面纵肋底缘达到屈服时对应的每延米截面弹性极限弯矩下降了3.7%，试件在纵肋底缘受拉屈服后仍有较高的安全储备。截面弯矩使用率分析表明，在连续支承钢-UHPC组合桥面板中，中支点截面更易成为控制设计截面。

（3）根据焊钉间距有限元参数化分析结果，相比于焊钉间距100 mm，增加焊钉间距至400 mm时，组合桥面板弹性阶段抗弯刚度下降了14.1%，开裂荷载等级显著提升了84.2%。此外，从截面弯矩使用率角度而言，短焊钉间距增大使得部分组合桥面板结构受力趋向于更为经济，但需注意过大的焊钉间距会导致焊钉疲劳破坏。

作者贡献说明：

徐晨：指导试验设计、数据分析、论文写作与修改。

张乐朋：参与试验设计、数据分析及论文初稿的写作与修改。

江震：参与试验设计与数值分析。

马骉：理论分析。