CGTY-2型陀螺全站仪方位角测量实验及其精度分析

2021-09-08倪先桃刘成龙

铁道勘察 2021年4期

倪先桃刘成龙朱晓

(1.中铁二院工程集团有限责任公司,成都 610031; 2.西南交通大学地球科学与环境工程学院,成都 611756)

1 概述

在地理南、北纬度75°范围内,陀螺仪可以实现任意测站点的真北方位测定[1-2]。陀螺定向测量不受天气、时间以及测量环境等多种条件的限制,可广泛应用于铁路隧道、地铁及矿山测量等工程建设。采用陀螺仪加测陀螺方位角的方法来检核地下导线边的方位,可有效限制地下导线边方位角测量误差的累积,进而提高地下导线的精度。

早期的陀螺经纬仪主要用于矿山测量领域,其定向精度较差,难以满足大型地下工程建设需要[3-5]。随着科学技术的不断发展,高精度陀螺全站仪正逐步取代传统的陀螺经纬仪,其寻北定向的效率有了明显提升,但测量精度及稳定情况尚不明确[6-7]。已有学者进行相关研究,赵志红针对我国在陀螺全站仪的研究与制造方面的现状,对索佳陀螺全站仪的性能进行详细实验研究[8];石震等结合我国自主研发的GAT高精度磁悬浮陀螺全站仪,提出了一种基于高精度控制网比对法的陀螺精度评定方法[9-10];郭彩立等通过GYROMAT 3000陀螺全站仪在重庆轨道交通工程中的应用,对影响陀螺仪定向精度的因素及应对措施进行总结[11]。以下基于前人的研究,利用CGTY-2型陀螺全站仪进行方位角测量实验,探寻其方位角测量的精度及稳定性情况,以期为长大铁路隧道洞内平面控制网中合理地加测陀螺方位角提供指导意见[12-15]。

2 CGTY-2型陀螺全站仪工程控制网方位角测量实验

为研究CGTY-2型悬挂带式陀螺全站仪方位角测量的精度及稳定性,设计基于CGTY-2型陀螺全站仪的工程控制网方位角测量实验,采用的工程控制网网形见图1,其中D153-D155和D152-D154为模拟布设在隧道进出口处的已知边,D146-D148和D165-D167为模拟布设在进洞及出洞方向的洞内平面控制网方位角待测边。利用本次测量实验中采集到的多源数据,对CGTY-2陀螺全站仪的方位角实测精度进行多方面比较分析。

图1 陀螺方位角测量实验控制网网形示意

2.1 陀螺全站仪仪器常数定义

由于陀螺仪在安装或调整不完善,使得陀螺仪轴的稳定位置(陀螺北方向NT)与地理子午线真北方向并不完全重合,两者间的夹角即为陀螺全站仪的仪器常数Δ。坐标北方向、陀螺北方向、真北方向与观测边OP之间的关系见图2,其中,γ0为O点的子午线收敛角。

图2 三北方向关系及仪器常数示意

当陀螺全站仪架设在地面点O,在已知方位角的观测边OP上进行定向测量时,对于OP边的坐标方位角α0、陀螺方位角αT及地理方位角A0,有

式中,α0为地面已知边的坐标方位角;γ0为测站O的子午线收敛角。对于确定的陀螺全站仪,可认为在短期时间内其仪器常数Δ是稳定的。对于地下待测边,上述关系依旧成立,则有

将式(2)代入式(1),有

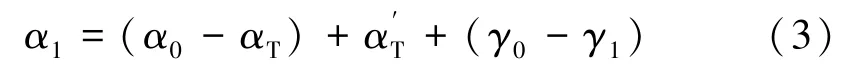
为方便仪器常数计算,将子午线收敛角计算与仪器常数区分开。定义常数C=(α0-αT),则

式中,α1为地下待测边的坐标方位角;Δγ为地面方位角已知边测站点和地下待测边测站点的子午线收敛角差值;为在待测边上测得的若干次陀螺方位角均值;边坐标方位角α0可由该边两端点的坐标反算得到。由上可知,陀螺全站仪仪器常数的测定精度对未知边坐标方位角测量成果的精度将会产生直接影响。

2.2 陀螺全站仪仪器常数的测定

根据TB 10101—2018《铁路工程测量规范》中相关要求,本次实验采用“陀螺全站仪先在地面已知边进行陀螺方位角测量,再在地下待测边进行陀螺方位角测量,最后再把陀螺全站仪搬回到地面已知边进行陀螺方位角测量”的测量流程,若前后两次测定的仪器常数互差满足规范限差要求,则取两次测定常数的最或是值作为仪器常数测定的最终成果。

本次实验陀螺全站仪方位角测量具体流程为:在模拟的隧道洞内待测边(控制边D146-D148和D165-D167)陀螺方位角定向测量前,先在地面已知边D153-D155上测定仪器常数,然后进行洞内待测边的定向测量,最后再回到地面另外一条已知边D152-D154上再次测定仪器常数,实验过程中,这两条地面已知边的坐标方位角通过GNSS静态相对定位测量方法获得,然后再按照上述测量流程,对洞外已知边和洞内待测边进行返测。

为深入分析陀螺全站仪仪器常数的特性及其精度情况,在两条洞外已知边上进行了3次往、返陀螺方位角测量,在洞内待测边上进行了两次往、返陀螺方位角测量,每次测量3个测回。由于本次实验只采用一台陀螺全站仪进行观测,每个测站观测完成之后的仪器搬站、重新架设、整平、仪器预热及寻北定向测量都需要花费时间,故3次观测在时间上不连续;同时,对于同一条观测边其往、返观测在时间上也不连续。

两条已知边上的3次往、返观测陀螺方位角观测值统计结果见表1、表2(已知坐标方位角:66°40′04.4″和66°09′15″),其中ΔαT为测回间陀螺方位角较差最大值的绝对值。

表1 已知边三次往、返测陀螺方位角观测值统计结果(观测边D153-D155)

表2 已知边三次往、返测陀螺方位角观测值统计结果(观测边D152-D154)

根据TB 10101—2018《铁路工程测量规范》中的相关要求,若定向测量采用的陀螺全站仪标称精度不低于±5″,则独立测回间的陀螺方位角较差不应大于15″,两次测定的陀螺全站仪仪器常数较差不应大于±8″。由表1可知,在任意时段内,测回间的陀螺方位角较差都满足规范中不大于15″的要求,但有的时段已经非常接近限差。

在两条已知边上由观测的陀螺方位角观测值计算的仪器常数Δ1和Δ2、Δ1与Δ2较差和Δ1与Δ2的均值¯Δ见表3,其中Δ1、Δ2分别为在已知边D153-D155、D152-D154上测定的仪器常数,因CGTY-2型陀螺全站仪的标称精度为±3.6″＜±5″,故根据相关规范的要求,Δ1与Δ2较差的限差应为±8″。

表3 仪器常数测定结果统计

由表3可知,虽然本次实验同一次同一条边往、返测的仪器常数较差均满足相关规范的要求,但是不同时间段仪器常数较差变化较大。初步分析认为,陀螺全站仪的仪器常数可能随时间推移而发生变化,测定的仪器常数因此具有某种“时效性”;另外,仪器常数必须依靠仪器本身来进行测定,其测定的精度与所使用仪器的定向精度、仪器的稳定性和可靠性、测量环境的变化以及已知边坐标方位角是否准确等密切相关,也不能排除上述因素导致这种差异出现的可能性。

3 陀螺全站仪方位角测量精度分析

测定仪器常数后,就可以对待测边的陀螺方位角观测值进行仪器常数改正和子午线收敛角之差改正,最后得到待测边的陀螺全站仪坐标方位角测量成果。陀螺方位角测量实验前,先对上述已知边、待测边的两端控制点都进行了GNSS静态相对定位观测,参照TB10601—2009《高速铁路工程测量规范》中一等GNSS平面网测量的精度要求,以待测边平差后的GNSS方位角作为基准值,然后将待测边的陀螺全站仪坐标方位角测量结果与GNSS测量的方位角结果进行对比,进而分析本次实验通过陀螺全站仪测量得到的坐标方位角的外符合精度;除此之外,为对洞内待测边的陀螺方位角观测值进行内符合精度分析,本次实验对洞内待测边也进行往、返陀螺方位角测量。

3.1 陀螺方位角测量结果内符合精度分析

通过对同一观测边进行往、返陀螺方位角观测结果的比对来进行内符合精度分析,该方法无需获得观测边的坐标方位角真值,同时也不需要事先测定陀螺全站仪的仪器常数,以及进行仪器常数改正、子午线收敛角之差改正等数据处理,这样得到的陀螺全站仪方位角测量结果的内符合精度比较客观。内符合精度检测与仪器常数Δ的测定过程是一致的,因此,也可通过已知边往、返测的陀螺方位角进行内符合精度分析。往、返测陀螺方位角与方向闭合差ωi之间有

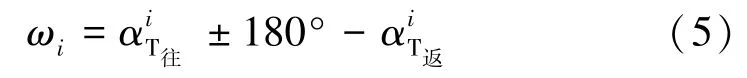
对本次实验中4条观测边的往、返测陀螺方位角按照式(5)计算后,即可得到CGTY-2陀螺全站仪方位角测量内符合精度情况,结果见表4。

表4 CGTY-2陀螺全站仪方位角测量内符合精度分析

由表4可知,方向闭合差ωi的一次定向中误差为

可见本次实验得到的CGTY-2型陀螺全站仪一次定向的中误差为±2.5″,优于该型号仪器的标称精度±3.6″。顾及到仪器对中误差和测量环境变化等对陀螺全站仪定向测量的不利影响,可以认为此次实验中CGTY-2陀螺全站仪的定向结果内符合精度较好。虽然陀螺全站仪测量的方位角内符合精度与仪器寻北定向的稳定性和可靠性相关,但其并不能完全代表陀螺全站仪方位角测量的精度和稳定性,还需要对其定向测量的外符合精度情况进行分析。