基于证据融合的固体发动机贮存寿命评估方法
2021-09-08李海阳周伟勇申志彬丁晓浩
郭 宇,李海阳,周伟勇,申志彬,丁晓浩
(1.国防科技大学 空天科学学院,长沙 410073;2.中国航天科工集团有限公司六院四十一所,呼和浩特 010010;3.中国人民解放军 96901 部队,北京 100095)
0 引言
固体火箭发动机(以下简称发动机)是固体导弹贮存中的薄弱环节,其贮存性能直接影响武器系统的使用寿命。因此,发动机贮存性能评价一直是产品研制中的重要工作[1]。受评估技术水平所限,同时为了简化研制工作,长期以来发动机的贮存性能研究主要集中于推进剂或药柱等材料或组件级的贮存寿命评价方法[2-5],并以这些薄弱环节的贮存寿命代表发动机整机的贮存性能。发动机贮存评价中难以得到充足的数据,以满足传统统计方法要求,并且有限信息中还包含着大量的主客观不确定性因素。系统复杂、样本量少一直是制约发动机寿命预估水平的难题。
相对传统概率论,证据理论的最大特点在于允许直接对集合或区间数赋予概率质量。当在实际中无法通过试验获取精确的测试数据或需要专家知识来判断的时候,这一特性将有利于描述来自不同渠道的不完整或不精确信息,并且证据提供的证据合成公式,可以根据多源信息得到一个更为可靠的估计[6]。近年来,为解决复杂系统小样本条件下的可靠性评估问题,许多学者尝试利用证据理论的证据融合和证据推理能力,解决系统可靠性信息利用不充分的难题,以得到更为可靠的评价结果[7-10]。但目前还未看到将证据理论用于发动机寿命预估中的报道。
本文运用证据理论,开展发动机贮存信息主客观不确定性研究,对这些异类数据和信息进行预处理和筛选,将相互冲突和矛盾的部分进行排除,并对相互印证的部分进行融合,用统一的数学模型来描述,对数据和信息进行综合利用,从而以统一的方法对发动机系统的可靠性进行评价。
1 发动机贮存性能数据信息及其特点
发动机工程实践中存在大量对贮存性能分析和评估有用的来源和形式多样的信息。按照信息来源分,发动机贮存数据主要分为三类:自然贮存试验、加速贮存试验和专家评价信息[11],各类信息的特点如表1所示。

表1 发动机三类贮存信息的特点
(1)自然贮存试验
发动机整机及其部件的自然贮存试验一般随导弹或单独在贮存环境试验场开展,有时也在研制单位仓库中开展。由于试验成本高昂,试验数量较少,一般只作为验证试验,因此评估结果置信度偏低。但自然贮存试验最能够真实反映产品在实际场景的贮存情况,信息真实性强,是进行贮存寿命评价一个最重要参考信息源,且权重一般都较高。
(2)加速贮存试验
为避免自然贮存试验的高费用、长耗时、评价滞后的缺点,常采取加速贮存试验来预测发动机的贮存可靠性。通过高应力下产品的失效特征来推断设计应力水平下产品的失效情况。发动机及部件的加速贮存试验一般参照行业或国军标[12-14]开展,试验数量一般较多,可获得指定置信度的贮存寿命。
(3)专家评价信息
发动机及其组件的设计专家,一般可以根据对比与类似产品的方案、选材、制造质量和使用环境等,判断给出所设计产品的可靠性,一般会给出一个偏保守的范围或上下限。
2 发动机贮存寿命评估方法
2.1 发动机贮存寿命评估框架和步骤
为充分利用上述各类贮存信息,先采用证据理论将各发动机单元(部件)贮存信息进行融合,再利用证据网络模型将串联单元的贮存信息传递到系统(发动机),进而实现其贮存寿命的评估,评估的框架如图1所示。
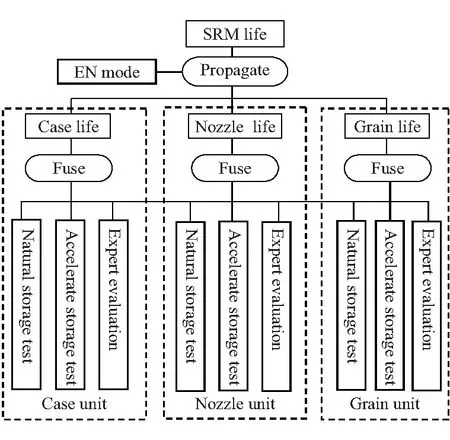
图1 发动机贮存寿命评估框架
评估步骤如下:
(1)将各个单元的各种来源的贮存信息进行处理,转化为基本可信度函数(BPA)——表示对某证据而不是其任何子集的信任程度[6]。
(2)根据实际情况,对各单元贮存信息的权重进行分配,并重新计算各信息源的BPA。
(3)利用证据理论,对单元的三类贮存信息进行合成,获得各单元贮存寿命的BPA。
(4)根据发动机的可靠性EN模型,将各单元贮存寿命的BPA通过证据网络传播到发动机整机系统,获得发动机贮存寿命的BPA。
2.2 单元贮存信息转化为BPA
发动机组件的各类贮存信息经过分析和处理后一般以概率形式给出,需要采用可传递信度模型将这些信息转化为证据信息。可传递信度模型(Transferable Belief Model,TBM) 是一个双层结构,分别是Credal层和Pignistic层。信度在Credal层进行传递,当要做出决策时,使用Pignistic Probability Transformation(PPT)得到Pignistic概率。在TBM中,Pignistic层首先由Credal层的信度函数构造出一个合理的概率分布。然后,以此概率分布为依据做出最终决策。
依据均匀分布的思想,通过pignistic转换[7,15-16]可将识别框架下对应的可信度平均分配到各焦元上,从而方便地对不确定情形做出决策,基本可信度分配函数转化为如下的赌博概率。
(1)
式中BetP(•)为赌博概率;Θ为贮存寿命识别框架;A、B为识别框架Θ的焦元;A∩B为焦元A和B的交集;| |为集合的基数;m(B)为识别框架Θ下焦元B的基本可信度函数。
在信息的约束下,会有多个基本可信度分配函数能满足上述的赌博函数要求,这里采用最小承诺(Minimal Commitment)准则进行可信度分配。最小承诺准则是Smets提出的一种基本概率分配函数生成理念,该方法将尽可能地将可信度分配给包含焦元基数最大的未分配集合或区间。依据最小承诺准则以及转换原理,概率到证据的转化方程为
(2)
式中T为发动机最长贮存寿命;m[0,T]和m[g,k]为寿命在[0,T]和[g,k]范围内的基本可信度;1-α为信息的置信水平。
2.3 单元贮存信息证据BPA的修正
由于不同信息源对产品可靠性的反应并不相同,在利用这些信息进行信息融合前,要考虑各个信息源的权重。依据认知程度,权重分配在遵循自然贮存>加速贮存>相似产品信息原则的基础上,可采用专家打分方法[17-19]等进行权重的确定。 分别将各个来源信息的权重定为W={ω1,ω2,…ωn}。首先,将权重进行归一化处理,令v=max(ω1,ω2,…ωn),则v1=ω1/v,v2=ω2/v,v3=ω3/v,v4=ω4/v,…vn=ωn/v。然后,分别对上文提及可靠性信息源生成的BPA进行修正,修正方法为
(3)
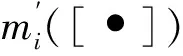
2.4 单元贮存寿命信息的证据融合
虽然发动机单元的贮存信息都是以产品寿命形式给出,但本质上是从不同的角度对产品可靠性进行评估,因而它们生成的基本概率分配函数可以认为是相互独立的,符合Dempster融合规则[15-16,20-21]。另外,发动机单元贮存信息源之间的冲突性一般比较低,采用传统的融合就可以,利用证据融合式(4)合成修正后的BPA。
(4)
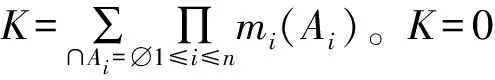
2.5 基于EN模型的系统贮存寿命评估
发动机系统可靠性可以用串联模型描述,即系统寿命由组成中寿命最短的单元决定,排除可更换单元后,其对应的基本可靠性框图如图2(a)所示,其对应的EN模型[9-10]如图2(b)所示。EN模型中,Pl为信任函数,Bel为似然函数,分别表示系统可靠度的上下界。其中,Ci表示串联模型的单元,1≤i≤n。若贮存寿命状态对应识别框架为{a,b,c},且:a∩b∩c=0,a∪b=ab,b∪c=bc,a∪b∪c=abc,状态关系如图3所示。
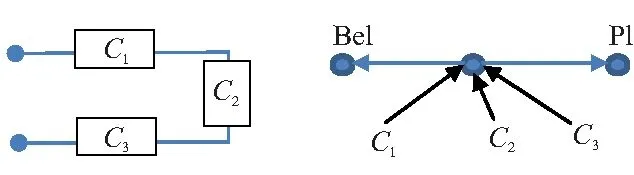
C1-Case,C2-Nozzle,C3-Grain

图3 贮存寿命状态识别框架关系图
当两个单元C1和C2串联时,其对应串联模型的真值表描述了系统状态和单元状态的逻辑关系,如表2所示。可见,只有当两个单元的寿命焦元相同时,系统寿命焦元相同;两个单元寿命焦元不相交时,系统寿命焦元为单元较低寿命焦元;当两个单元寿命焦元不相等并存在交集,且寿命下限相同时,系统寿命焦元为两单元焦元相交部分;当两个单元寿命焦元不相等并存在交集,且寿命上限相同时,系统寿命焦元取范围较大单元;当两个单元寿命焦元不相等并存在交集,且两者寿命上、限都不相同时,系统寿命焦元为含寿命下限部分区间和相交部分。两单元串联系统的BPA可以表示为m(Sys)=m1(C1)⊙m2(C2)。根据EN模型BPA分布,可以得到含两个单元串联系统的后验BPA分布。
当串联模型中含有多个单元时,也可以得到其系统的BPA分布。当串联模型中含有n个部件时,其系统的BPA为
m=m1⊙m2⊙…⊙mn=(((m1⊙m2)⊙…)⊙mn)
(5)
其中,mi(i=1,2,…n)表示串联模型中父节点的先验BPA分布,而m表示系统子节点的后验BPA。再对系统基本可信度函数mass函数进行pignistic转化,可得到发动机贮存寿命的概率分布函数。

表2 “与”门在转化为EN模型的焦元值表
3 某发动机贮存寿命评估
3.1 相关贮存信息和试验数据
某具有较强继承性发动机延寿研究中,其不可更换组件(壳体、喷管、药柱)的贮存可靠性信息见表3(未考虑点火装置、密封圈等可更换部件)。
其中,加速贮存试验开展比较充分、样本量较多,信息给出贮存寿命的置信度为90%;自然贮存试验数量极少,信息给出贮存寿命的置信水平取70%;专家评价是参考多个产品贮存结果给出的结论,贮存寿命的置信度取80%。由于自然贮存试验结果最可信,其权重最高;加速试验结果具有客观性,但很难严格符合失效机理一致的假设,信息的权重较自然贮存低;而专家评价是主观判断,权重最低。经过专家评价,各组件证据中自然贮存信息的权重0.5,加速贮存权重0.3,专家评价权重0.2。另外,根据发动机技术现状,认为其理想贮存寿命为35 a,并作为基本可信度转化时发动机寿命的上限。
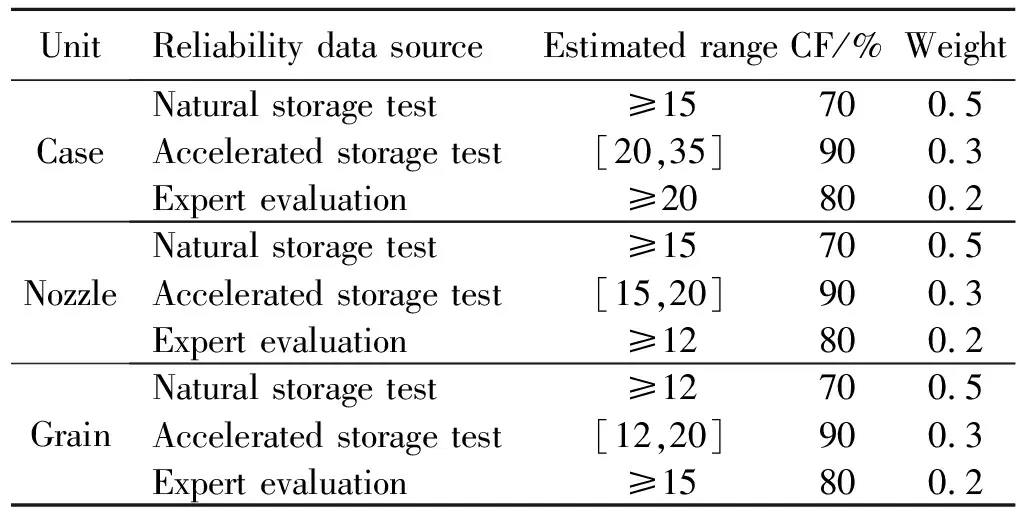
表3 某发动机可靠性数据
3.2 各可靠性信息源BPA的计算
根据式(2),药柱自然贮存试验、加速贮存试验、专家评价信息对应的单元BPA分配函数分别为式(6)~式(8)。
(6)
(7)
(8)
对上面3个方程式求解,可得壳体寿命的BPA。同理,根据表3中数据,也可以求得喷管和药柱单元寿命的BPA,结果见表4。
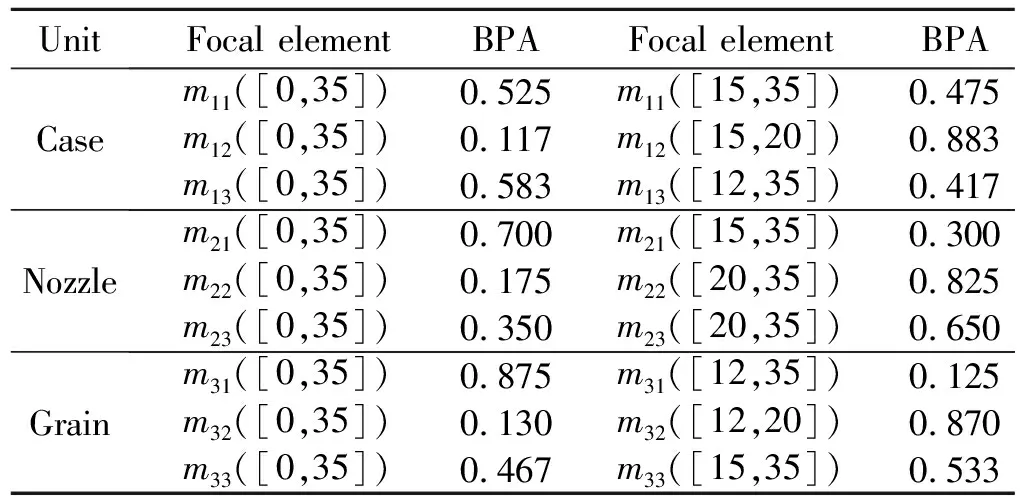
表4 壳体、喷管和药柱贮存信息的BPA
3.3 各信息源BPA的修正
各个信息源的权重为W={0.5,0.3,0.2},按照第2.2节中的方法,取v=max(W1,W2,W3)=0.5,则V=(1,0.6,0.4),并根据式(3)对第3.2节中的初步分配结果进行修正,各单元BPA的修正结果见表5。

表5 发动机各个单元贮存信息修正后的BPA
3.4 各单元贮存寿命的证据合成
发动机系统中的3个单元的3列信息源生成的mass函数的证据冲突K=0,说明信息源之间的相互冲突程度很小,可以利用D-S证据组合公式(4),得到合成的mass函数,见表6。
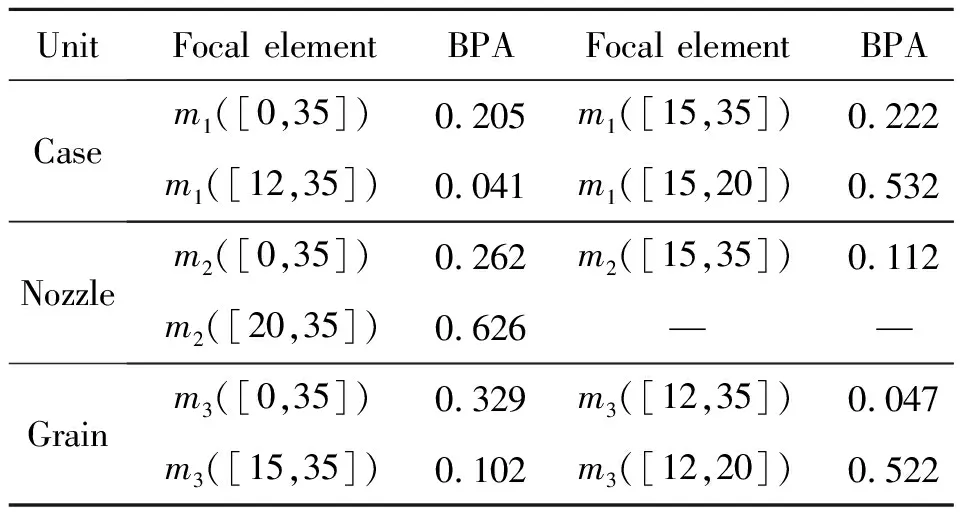
表6 发动机各个单元BPA的合成结果
3.5 发动机系统寿命概率分布的计算
根据各个单元贮存寿命的可信度分配函数,确定发动机贮存寿命识别框架为{[0,35]}。其中,含互补焦元[0,12],[12,15],[15,20],[20,35]。
依据式(5),对表6中3个单元寿命PBA进行计算,得发动机系统寿命的BPA,结果见表7。
根据上述系统BPA数据,通过pignistic转换得到发动机贮存寿命分布函数,见式(9)和图4。

(9)
经计算,不考虑可更换部件的条件下,该发动机中位寿命为15.59 a,80%置信水平贮存寿命下限为9.62 a。结果与表3数据比较吻合,也与发动机首翻寿命(9 a)接近。

表7 发动机系统的BPA结果

图4 发动机贮存寿命分布函数
4 结论
(1)首次构建了串联系统EN模型的贮存寿命识别框架,并提出了其“与”门焦元证据转换法则,打通了寿命证据由单元向系统传递的路径,建立了系统级证据理论寿命评估方法,具有一定的理论意义。
(2)首次将证据理论用于寿命评价,以实例进行了某发动机3个串联单元、3类贮存信息的证据融合和传递,贮存寿命评估结果准确度较高,具有较强的工程应用前景。
(3)贮存寿命证据合成时,其上限和信息源权重的确定都具有主观性,对评价结果有一定影响,发动机寿命评估工程应用前应固化或确立权重和理想寿命确定方法,并形成成套寿命评价标准和软件系统。
(4)导弹武器系统贮存寿命不能用简单的串联模型来描述,复杂系统的EN模型及其分析技术是决定该方法能否推广应用的关键。其中,贮存寿命识别框架下各个逻辑门焦元证据转换法,则是本方向下一步研究的重点。
