巧辨真假
2021-09-07李致远
发明与创新·小学生 2021年7期
李致远


有7枚完全一样的钱币,其中5枚是真币,重量相同,另外两枚是假币,要重一些。现在有一架没有砝码的天平,需要进行多少次称量,才能确保找出两枚假币?
答案解析
题目的关键在于确保找出两枚假币,运气好的话,能轻而易举地找到假币,所以需要考虑的是运气差时的情况,如果那时我也能找到,就可以确保找到假币。
开始,我准备用天平去称,但一个一个地称,太繁琐。我决定用分组法称量,因为假币肯定会在某一组或两组中,通过比较相同数量钱币的重量,能确定假币范围。
我将7枚钱币依次编号为①—⑦。如何分组呢?如果分成2组——4枚钱币一组,另外3枚钱币一组,数量不均匀,所以确定最少要分成3组。
如果分成3组且保证最少有两组钱币数量相同,有3种分法:(3、3、1),(2、2、3),(1、1、5),其中(1、1、5)这种分法意义不大,因此分别研究前两种情况,用画图的方式来呈现。
第一种情况,7枚钱币被分为3组:第一组(①②③)、第二组(④⑤⑥)、第三组(⑦),研究过程如图1。
可知,最多进行3次称量,就可以确保找出假币。
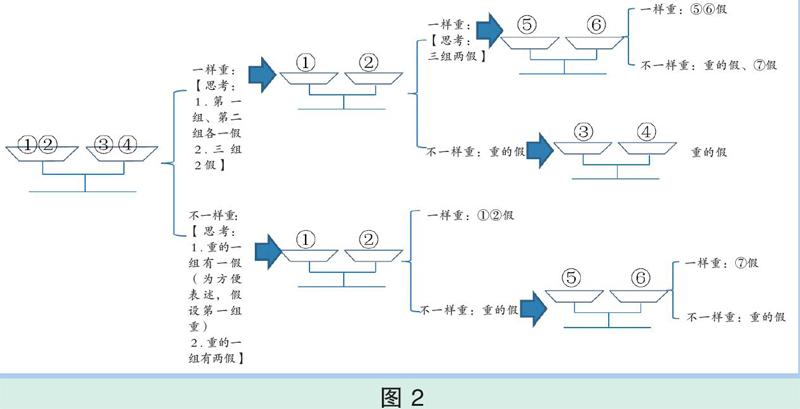
第二种情况,7枚钱币被分为3组:第一组(①②)、第二组(③④)、第三组(⑤⑥⑦),研究过程如图2。
可知,最多也只需进行3次称量,就能确保找到假币。
通过比较,我发现第二种分组比第一种分组数量平均些,组内的钱币数量差距较小,方法更简便。采用第二种分组法,运气好的话,只需要进行两次称量,就能找到假幣。
指导老师 颜玉兰
