船机油液非铁磁性金属颗粒区分检测方法研究

吴 瑜，韩华翔，张朝骅，王科霖，杨 超

(1.上海海洋大学工程学院，上海 201306；2.上海海洋可再生能源工程技术研究中心，上海 201306；3.上海海事大学商船学院，上海 201306)

0 引言

油液作为润滑剂广泛应用于工业中，在润滑系统中固体颗粒是主要的污染物，约35%的柴油机运行故障、38.5%的齿轮失效以及40%的滚动轴承失效是由于油液污染引起的[1-4]，因此保持船机油液的清洁对于延长船机系统工作寿命具有十分重要的意义。电感检测是常用的金属颗粒检测方法之一，它具有很多优点：可区分颗粒的电磁属性，结构简单，经济性好，寿命长等。近年由于微制造技术的发展，结合微流体电感芯片能够实现颗粒计数统计和尺寸测量，电感检测法能更加精确判断船机设备的磨损状态[5-8]。

船机的摩擦副表面常会涂有非铁磁保护层。如合金钢材质的活塞头、浇铸白合金的滑块、青铜承磨环、合金的轴承与轴瓦以及为提高耐磨性采取的镀铬或镀铜措施。因而针对船机油液检测，非铁磁性金属颗粒的定性、定量分析，是判断摩擦副磨损状况(如磨损部位与程度)，实现精准故障预测与诊断的关键环节[9-11]。但是目前电感式油液检测只能够利用金属颗粒的磁导率，对金属颗粒的电磁属性进行判断。非铁磁性金属颗粒因其相对磁导率约等于1，磁化理论建模方法并不适用，而目前针对电感式传感器检测非铁磁性金属颗粒的理论研究还较少[12-15]。

本文通过构建线圈电感变化量与金属颗粒电导率间的关联函数，结合实验测得非铁磁性金属颗粒流经时线圈电感的变化量，利用函数关系得到非铁磁性金属颗粒的电导率，从而实现不同材质非铁磁金属颗粒的区分检测。

1 理论分析

1.1 数理模型的建立

电感式微流体芯片的结构如图1所示，线圈内检测区域是微流体芯片中最重要的部分，当非铁磁性金属颗粒流经该交变磁场检测区域时，使线圈周围的磁场强度降低(楞次定律)，该变化反过来使线圈的磁通量减少，从而引起线圈阻抗的降低。具有不同电导率的颗粒产生不同的涡流，导致线圈内的磁通量变化也不同，因此，可以用通电线圈的电感变化来检测金属材料的电导率，从而区分出非铁磁金属颗粒的材质[16]。

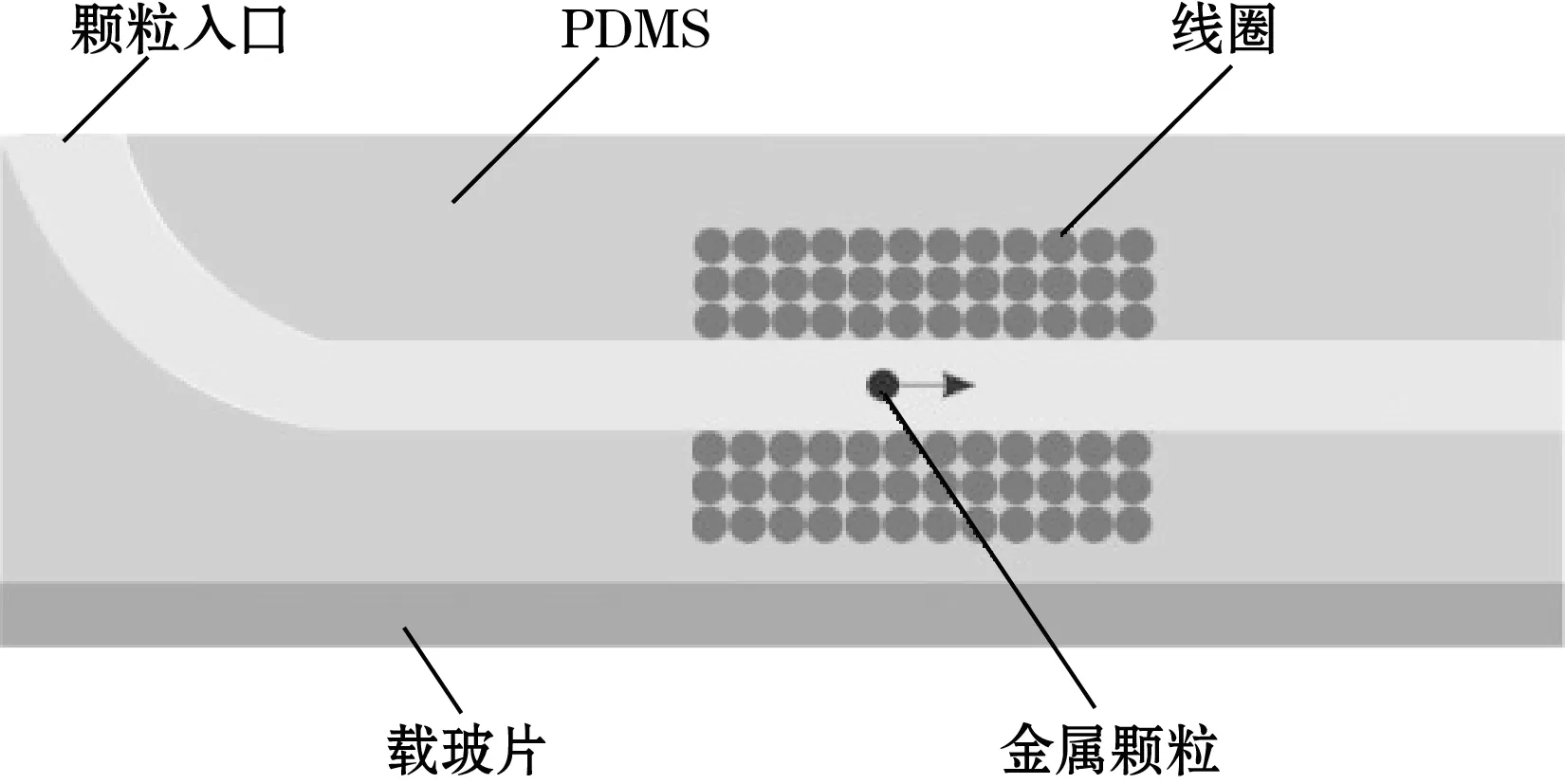
图1 微流体芯片结构示意图

如图1所示，检测芯片主要由螺旋电感线圈(电感式微流体检测芯片的主要部件，具有微传感器的作用)、微流道、载玻片、PDMS等部分组成。线圈部分为40 μm线径铜丝绕600圈制成的内径为1.5 mm、外径为2.9 mm螺线管空心圆柱。

1.1.1 线圈的阻抗增量表达式

在场中引入动态标量位和修正动态磁矢势,可得：

(1)

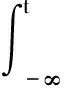
(2)

式中：φ为动态标量位；E为电场强度；A为磁矢势；A*为修正动态磁矢势。

电场强度及磁感应强度可以表示为

(3)

B=▽×A*

(4)

式中B为磁感应强度。

线圈的磁链和线圈两端的感应电压可以表示为

(5)

(6)

式中：Ψ为多匝线圈产生的磁链；V为线圈体积；λ为线圈匝数密度；J为线圈电流密度，J=λIe；I为线圈电流；e为线圈电流密度矢量方向。

线圈的阻抗Z=U/I，Z为线圈阻抗，U为线圈两端电压。从而得到当金属颗粒经过时，线圈的阻抗增量可以表示为

(7)

式中：ΔZ为线圈阻抗的变化；Z0为金属颗粒流经前线圈的阻抗值；j为虚数单位；ω为交流源的频率。

利用关系式

E=-jωA

(8)

可以得到线圈的阻抗增量跟磁矢势的关系：

(9)

式(9)是线圈阻抗增量的表达式。

1.1.2 金属颗粒在时谐场中对周围磁场空间散射场

建立如图2所示的数理模型，取球面坐标系(r,θ,φ)。

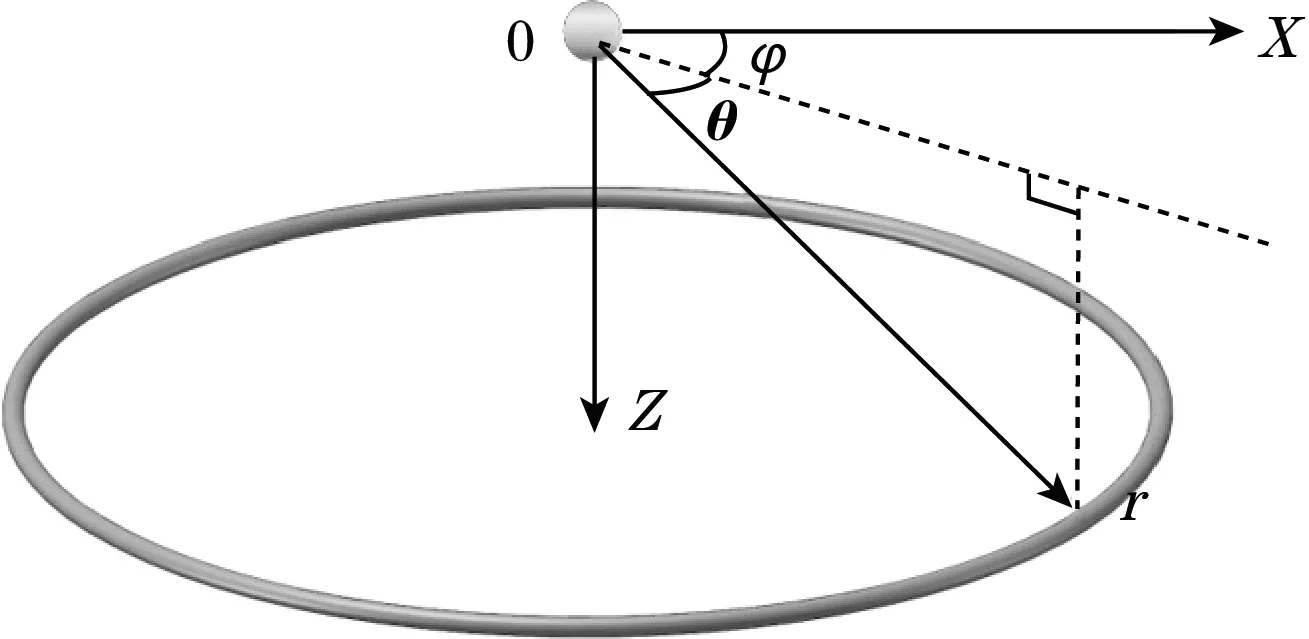
图2 球形金属颗粒磁化模型

将麦克斯韦方程组拓展到时谐磁场中，得到以下基于复数形式的麦克斯韦方程组：

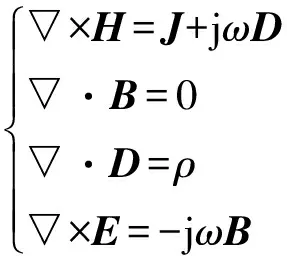
(10)

式中：H、D分别为磁场强度和电通量；ρ为自由电荷体密度。

并且满足以下条件：

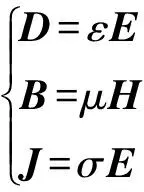
(11)

式中：ε为金属介电常数；μ为金属磁导率；σ为金属电导率。

根据Maxwell方程组和磁矢势的定义B=▽×A，取洛仑兹规范，可得磁矢势A满足的约束方程为

▽2A+k2A=0

(12)

式中：k2=-jωμrμ0σ；μr为金属相对磁导率；μ0为真空磁导率。

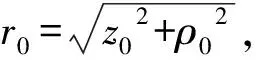
|A|r→0<∞

(13)

(14)

(15)

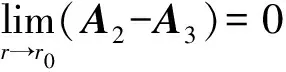
(16)

(17)

式中：I为圆环线圈中复数形式的电流；δ为D函数，θ0=arcsinρ0/r0。

结合边界条件，通过分离变量法求得磁矢势的解析式：

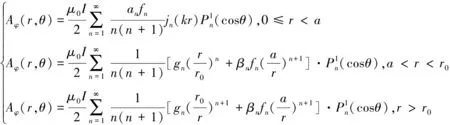
(18)

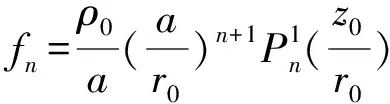
(19)

(20)

(21)

(22)

(23)

金属颗粒对圆环线圈的散射场为

(24)

设空心圆柱线圈内半径、外半径、轴高以及到金属颗粒的距离分别为R1、R2、2C以及H。以金属颗粒的半径a为基准量，归一化量为r1=R1/a，r2=R2/a，c=C/a，h=H/a。

求得金属颗粒外对空芯圆柱线圈的散射场如下：

(25)

式中I为线圈中复数形式的电流。

(26)

(27)

把式(25)代入式(9)，整理后得：

(28)

λ可以用线圈的匝数W表示：

(29)

从而得到线圈电感变化为

(30)

式中ΔL为线圈电感的变化。

1.2 电感变化量的计算

根据式(30)，线圈电感的变化与金属颗粒、线圈的物性参数，线圈激励电流、频率相关。可将式(30)写成如下表达式：

ΔL=F(σ,μ,I,f,x)

(31)

式中：f为线圈激励源的频率；x为金属颗粒中心到线圈中心处的位置。

在式(31)中，假设除电导率σ，其他参数都为常数，则线圈的电感变化量ΔL就是σ的单值函数。因此，可以通过测量线圈的电感变化量来计算颗粒的电导率，区分检测非铁磁性金属颗粒的材质。

en[n_Integer,r1_Real,r2_Real,h_Real,c_Real]∶=

NIntegrate[η1-n·Integrate[ξn-2·Legendrep[n,1,ξ],

GenerateConditoons→False,Assumptions→η>0],

{η,h-c,h+c},AccuracyGoal→3,MaxPoints→1000]

2 实验验证

图3为油液颗粒检测系统图，注射泵驱动油样以恒定速度在微流道中流动。阻抗分析仪(E4980A)作用为：产生高频交流源；实时记录线圈的电感分量，并把数据传输到计算机中。

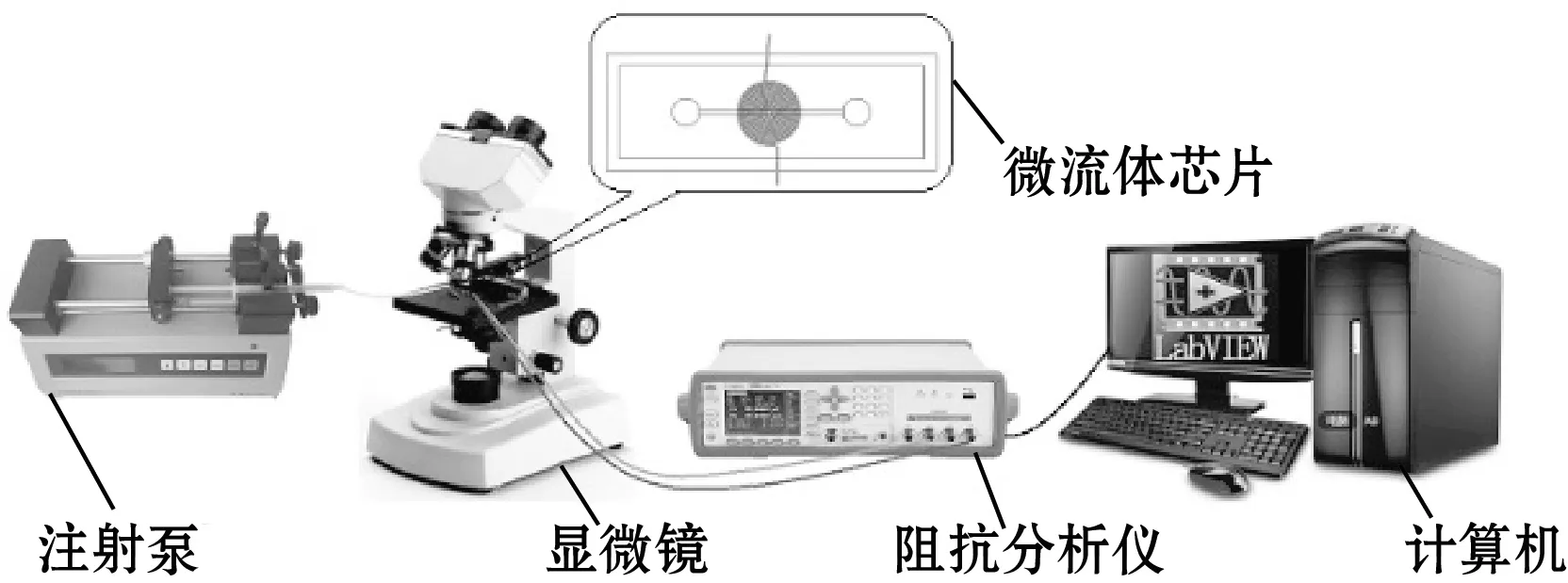
图3 检测系统示意图

用精密天平(XS225A)称重10 mg粒径为860～880 μm的铝和铜颗粒，如图4所示，将其加入50 mL的Hyspin AWS10液压油中混合。测试时，将注射泵的速度设置为0.5 mL/min，激励源的频率设置为2 MHz。

(a)铜颗粒

(b)铝颗粒图4 显微镜下金属颗粒照片

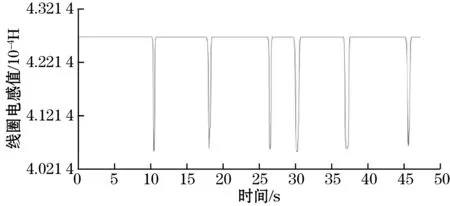
一种金属颗粒做4组实验再求平均值，其中实验一的电感信号如图5、图6所示。

(a)

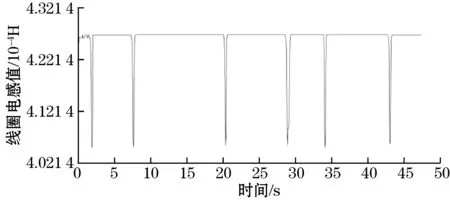
(b)图5 铜颗粒检测的电感脉冲片段

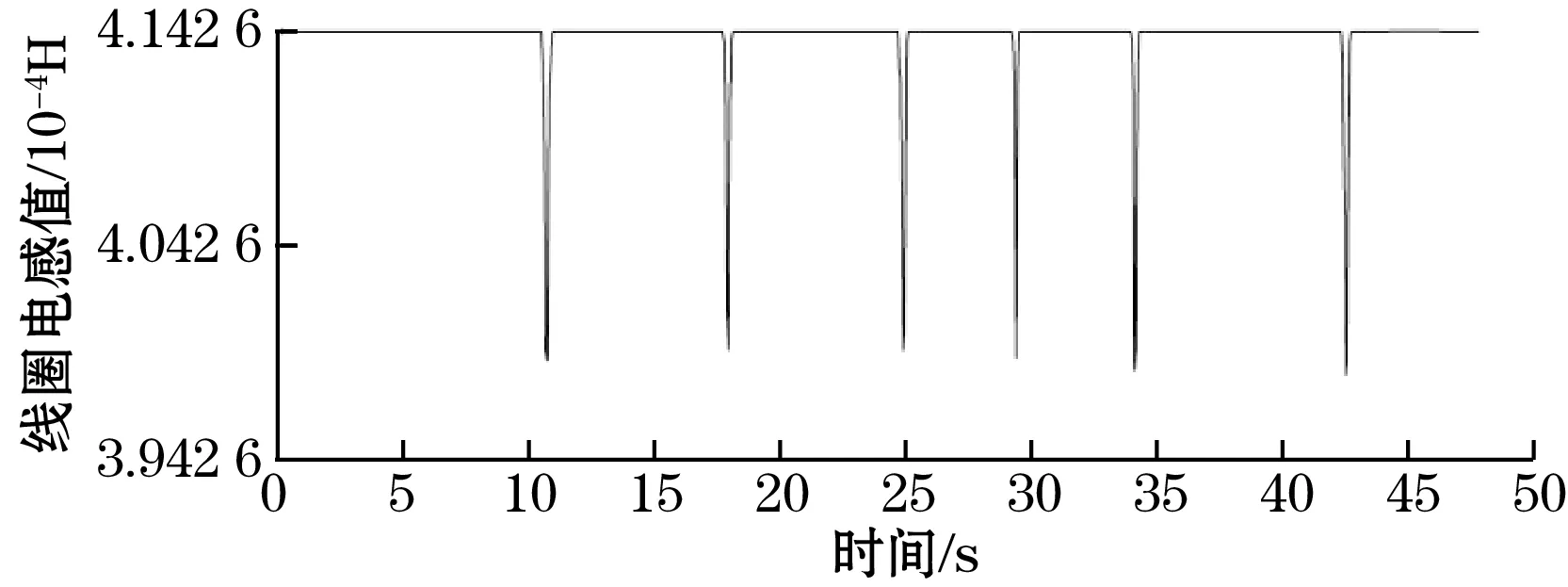
(a)

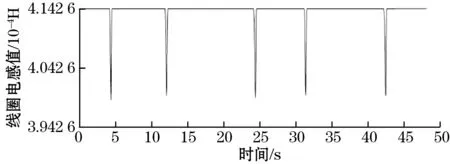
(b)图6 铝颗粒检测的电感脉冲片段

通过整理实验结果，得线圈的电感变化量为ΔL铜=-3.845 6×10-5H，ΔL铝=-3.663×10-5H。而铜颗粒的L基础电感=6.93×10-4H，铝颗粒的L基础电感=6.9×10-4H，从而得到ΔL铜/L基础电感=-0.055 49，ΔL铝/L基础电感=-0.053 1。通过函数关系，反过来得到铜颗粒的电导率为6.71×107S/m，铝颗粒的电导率为4.05×107S/m。已知铜的真实电导率为5.8×107S/m，铝的电导率为3.5×107S/m，则计算得到的电导率与材料真实电导率符合程度分别为15.6%、15.7%。

3 结论

金属颗粒的定性、定量分析，是实现精准故障预测与诊断的关键环节，但是目前电感式油液检测只能利用金属颗粒的磁导率，对金属颗粒的电磁属性进行判断，非铁磁性金属颗粒检测的理论还较少。本文基于麦克斯韦方程组建立微电感线圈检测非铁磁性金属颗粒的时谐场边值理论模型，用分离变量法得到金属颗粒的散射场解析解，进而明确非铁磁性金属颗粒流经时线圈电感变化解析式。再根据实验测量得到铜颗粒和铝颗粒流经线圈时，线圈电感的变化分别为ΔL铜/L基础电感=-0.055 49，ΔL铝/L基础电感=-0.053 1，通过线圈电感与金属颗粒电导率的函数关系得到铜颗粒的电导率为6.71×107S/m，铝颗粒的电导率为4.05×107S/m，与铜和铝的真实电导率符合程度良好，从而区分出不同材质的非铁磁金属颗粒。