中高频椭圆铰链双光纤光栅加速度传感器

李立新，孙 睿，于瑞红，高志涛，邱忠超

(防灾科技学院电子科学与控制工程学院，河北廊坊 065201)

0 引言

铁路、桥梁的中高频振动会严重影响结构健康，带来威胁[1]。可以通过测量加速度反映大型结构的振动情况。光纤布拉格光栅(fiber Bragg grating，FBG)加速度传感器作为一种无源器件[2]，与传统机电式加速度传感器相比，具有测量灵敏度高、电磁不敏感、可分布式测量等优点[3]，使其在监测大型结构中高频振动方面的应用具有重要意义。

近年来，FBG传感技术不断发展，FBG加速度传感器成为新的研究方向，并被广泛应用于地震监测[4]、石油化工[5]、大型工程[6]和健康监测[7]等领域。王宏亮等研制了一种等强度双悬臂梁的FBG加速度传感器，实现50 Hz的低频信号实时监测，灵敏度为208.5 pm/g[8]。贾振安等研制了一种悬臂梁式FBG振动传感器，该传感器的谐振频率为90 Hz，平坦区域为10～50 Hz，传感器灵敏度为121 pm/g2[9]。O. P. Parida等设计了一种新型双L悬臂梁FBG加速度传感器，与单L悬臂梁FBG加速度传感器相比，提高灵敏度的同时实现了温度自补偿，其灵敏度为406.7 pm/g[10]。N. Gutiérrez等研究了一种空心六边柱体FBG加速度传感器，小型化、质量轻是该传感器的重要优势。同时这种结构降低了传感器的灵敏度，实验验证该传感器的灵敏度仅为19.65 pm/g[11]。然而，目前FBG加速度传感器的研究多集中在中低频范围，对中高频FBG加速度传感器的研究较少。

本文提出一种基于椭圆铰链的中高频双FBG加速度传感器，利用椭圆铰链无机械摩擦的优点[12]和差分[13]解调法，实现灵敏度倍增的效果。通过传感器理论模型分析传感器的灵敏度和谐振频率，采用MATLAB和ANSYS软件对传感器的结构参数进行优化及仿真分析，得到传感器的结构参数。研制传感器并进行灵敏度标定实验，验证并分析实验结果。

1 传感器结构设计

1.1 传感器工作原理

双FBG加速度传感器由椭圆铰链、2根FBG、质量块、固定支架组成，如图1所示。FBG一上一下粘贴在质量块和固定支架之间，FBG的两端在粘贴时施加相等的预应力，以防止出现啁啾效应。当传感器处于静止状态时，上下光纤光栅不受力，因此光纤中心波长不会发生变化。当传感器振动时，质量块在惯性力的作用下以椭圆铰链的质点为中心转动，同时带动上下FBG产生伸缩形变，进而引起FBG的反射波长发生漂移。最终，通过解调中心波长的变化情况获取中心波长变化量和加速度之间的关系。

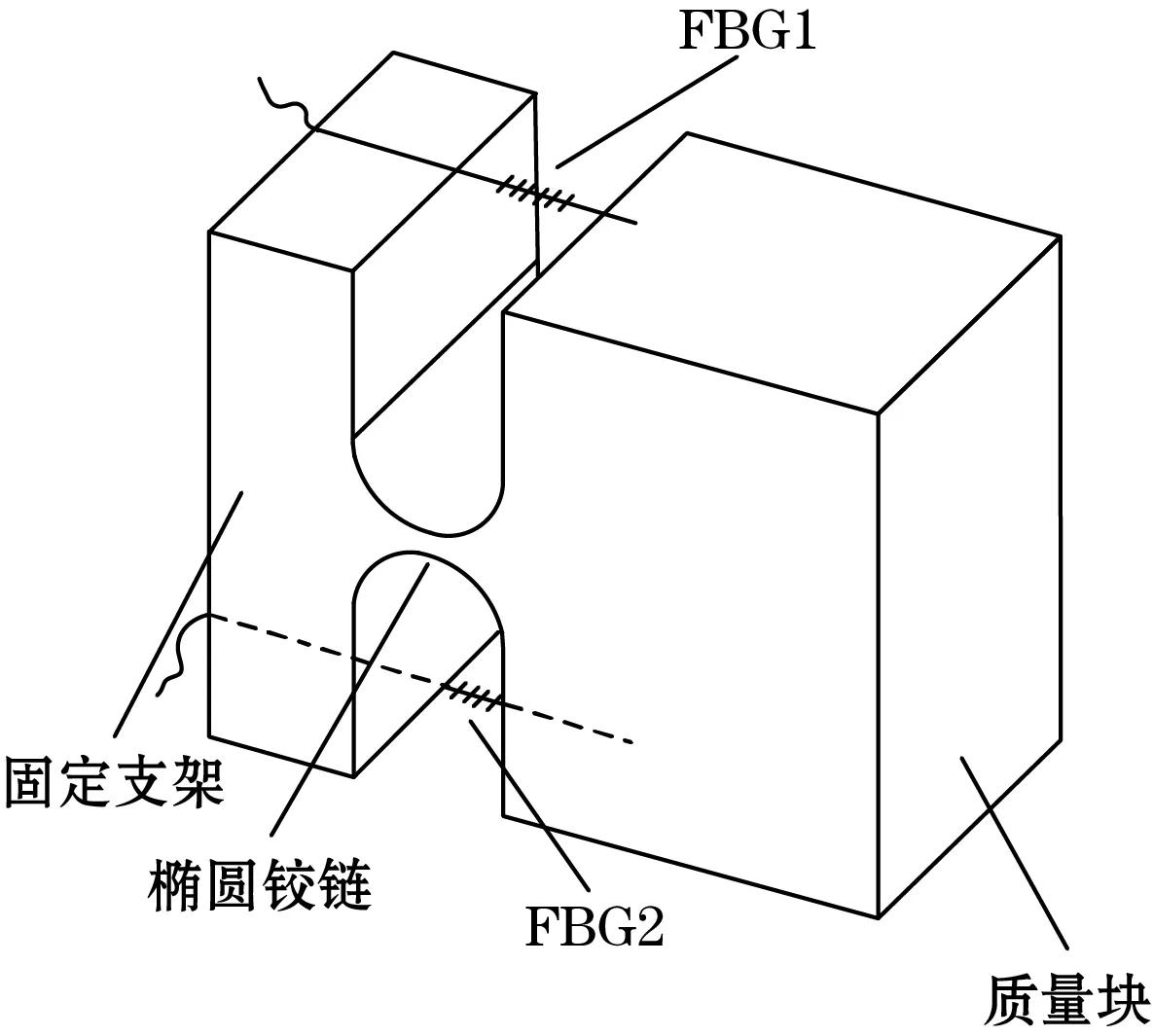
图1 传感器结构

FBG中心波长的漂移和应变紧密相关，两者之间的关系可表示为

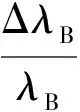
(1)

式中：Pe为有效弹光系数，通常取0.15～0.22；ΔλB为FBG的中心波长在应变作用下的漂移量；λB为FBG中心波长；ε为FBG产生的轴向应变。

1.2 传感器灵敏度分析

传感器的结构尺寸及力学模型如图2所示。以一根FBG为例，分析传感器的理论灵敏度。在传感器的竖直方向施加大小为g(g=9.8 m/s2)，方向向上的加速度时，由牛顿第三运动定律可知，质量块以铰链为中心振动。

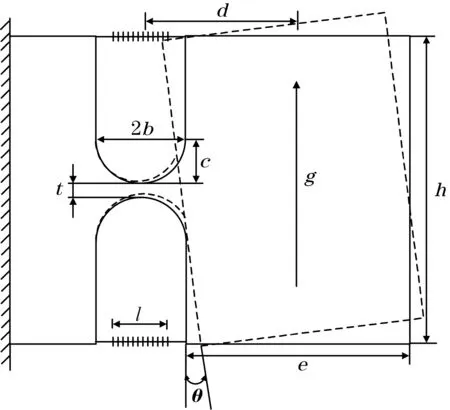
图2 传感器结构振动模型

由力矩平衡方程，可得

(2)

式中：m为质量块的质量；d为铰链中心到质量块中心的距离；k为光纤弹性系数；Δl为光纤的应变量；h为质量块的高度；K为椭圆铰链的转动刚度；θ为椭圆铰链的转动角度。

椭圆铰链的转动刚度K为

(3)

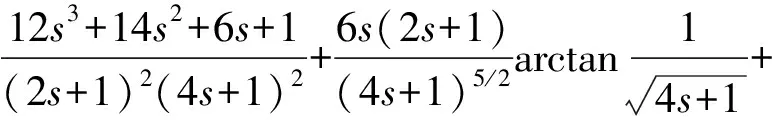
(4)

式中：E为传感器材料的弹性模量；w为椭圆铰链的厚度；b为椭圆铰链的长半轴；s=c/t；c为椭圆铰链的短半轴；t为椭圆铰链最薄处的厚度。

传感器灵敏度S为FBG的中心波长变化量Δλ和加速度a之比，即

(5)

式中εf为光纤产生的应变。

以上是单FBG的灵敏度分析，因为双FBG是一上一下对称粘贴，在同一时刻，一根FBG拉伸，另外一根FBG必然收缩。两根FBG反射波长的变化情况相反，因此，将两根FBG的反射波长做差求得波长漂移量，得到传感器灵敏度为单FBG加速度传感器灵敏度的2倍。

1.3 传感器谐振频率分析

谐振频率f与传感器能够测量的频率范围密切相关，谐振频率越高，传感器可测频率范围越宽，传感器的灵敏度越小。

传感器谐振频率为

(6)

转动惯量J为

(7)

2 结构分析优化与仿真

2.1 结构参数对传感器性能的影响

由传感器灵敏度分析可知，两点粘贴式的FBG加速度传感器光栅长度l只与灵敏度有关，与谐振频率无关。此外，传感器的灵敏度和谐振频率与椭圆铰链的长半轴b、短半轴c和厚度t等尺寸密切相关。传感器制作材料选用弹簧钢，其密度为7 800 kg/m3，弹性模量为210 GPa，光纤的弹性模量为72 GPa，有效弹光系数为0.22，光纤光栅的中心波长为1 553 nm，长度l为5 mm。

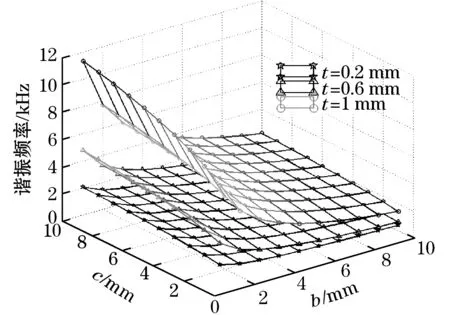
分析在不同的铰链厚度t下，椭圆铰链长半轴b、短半轴c对传感器灵敏度和谐振频率的影响。令质量块的质量m=18.72 g，b,c∈(0 mm,10 mm)，当椭圆铰链的厚度分别为0.2、0.6、1 mm时，得到的灵敏度和谐振频率变化情况如图3所示。

(a)b、c对灵敏度的影响

(b)b、c对谐振频率的影响图3 椭圆铰链长半轴b、短半轴c对灵敏度、谐振频率的影响

由图3可知，当椭圆铰链的参数发生改变时，传感器的灵敏度和谐振频率均发生变化。当椭圆铰链的长半轴b增大时，传感器的灵敏度增大，谐振频率减小；当椭圆铰链的短半轴c增大时，传感器的灵敏度减小，谐振频率增大；当椭圆铰链的厚度t增大时，传感器灵敏度减小，谐振频率增大。因而需要对椭圆铰链的结构参数进一步优化，得到最优的灵敏度和谐振频率。

2.2 结构参数优化

采用MATLAB优化工具箱对传感器的椭圆铰链长半轴b、短半轴c和厚度t进行优化，得到最优的灵敏度和谐振频率。令式(4)中的s∈(1,7)，运用MATLAB对参数s进行多项式拟合，得到

f(s)=0.000 36x4-0.007 7x3+0.063x2-0.26x+0.71

(8)

式(8)的拟合确定系数和均方差值分别为0.999 7和0.001 2。将式(8)带入式(4)中，再利用MATLAB进行参数优化。设定传感器的灵敏度和谐振频率为目标参数，以椭圆铰链的长半轴b、短半轴c和厚度t的取值为约束条件，结合MATLAB优化工具箱建立优化模型，考虑到传感器的尺寸和加工的可能性，得到优化模型为

MAXS
s.t. 100 Hz≤f≤800 Hz
1 mm≤b≤7 mm
1 mm≤c≤6 mm
0.2 mm≤t≤3 mm
2≤b/t≤5

(9)

由优化结果可知，当椭圆铰链长半轴b为2.578 mm，短半轴c为2.081 mm，椭圆铰链的厚度t为0.791 9 mm时，可得到最优的灵敏度和谐振频率。考虑到机械加工精度问题，最终b、c和t的取值分别为2.6 mm、2.1 mm和0.8 mm。

2.3 ANSYS仿真

采用上述优化得到的结构参数对传感器进行建模，并导入ANSYS进行仿真分析。首先将模型导入ANSYS静应力仿真工具中，对传感器模型的固定支架施加固定约束，对传感器整体施加标准地球重力加速度g的外部载荷，得到模型的应变云图，如图4所示。

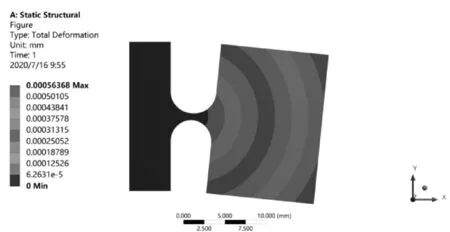
图4 静应力仿真分析

由图4可知，传感器自由端产生的形变最大，并且向固定端逐渐减小，自由端的最大形变量为0.56 μm。

依据静应力分析的结果对传感器模型进行模态分析，得到的一阶模态谐振频率分别为764.82 Hz、二阶模态的谐振频率为5 101.4 Hz，且二阶模态为转动振型，如图5所示。

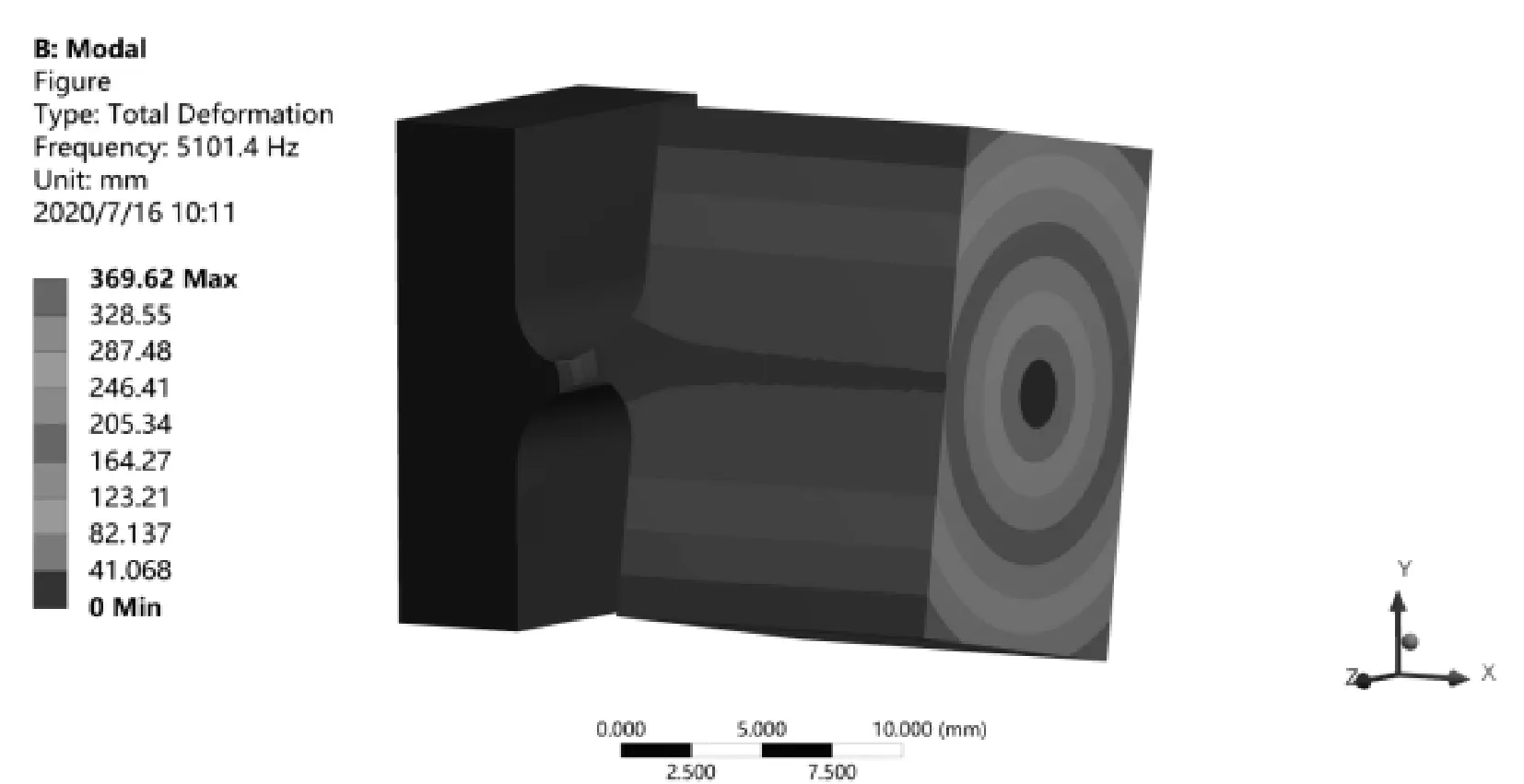
图5 模态仿真分析

由图5可知，二阶模态传感器模型在外界激励作用下沿X轴产生转动。此外，ANSYS仿真分析发现，传感器各阶谐振频率相差较大，表明该结构传感器的交叉耦合小，可以减弱交叉干扰。

最后进行谐响应分析，对传感器模型的固定支架施加固定约束，分析不同频率正弦载荷作用下的系统动态响应。设置频率变化为0～900 Hz，步长为10 Hz，正弦载荷大小为4g，得到的传感器动态响应如图6所示。

图6 谐响应仿真分析

由图6可知，传感器的谐振频率约为780 Hz，且在500 Hz以下曲线相对平缓，有利于实现中高频的测量。

3 传感器标定实验

对双FBG加速度传感器进行灵敏度标定实验，以确保传感器在500 Hz以下具有良好的线性响应。光源、振动台配套系统和信号解调系统共同组成传感器灵敏度标定实验系统。信号解调系统包括波长解调仪、计算机等，如图7所示。设计的传感器底座与振动台之间通过螺栓紧密连接，FBG的反射光波通过传输光纤介入环形器，最终输送至解调仪，解调出光波波长变化所携带的信息，实验环境温度为25 ℃。

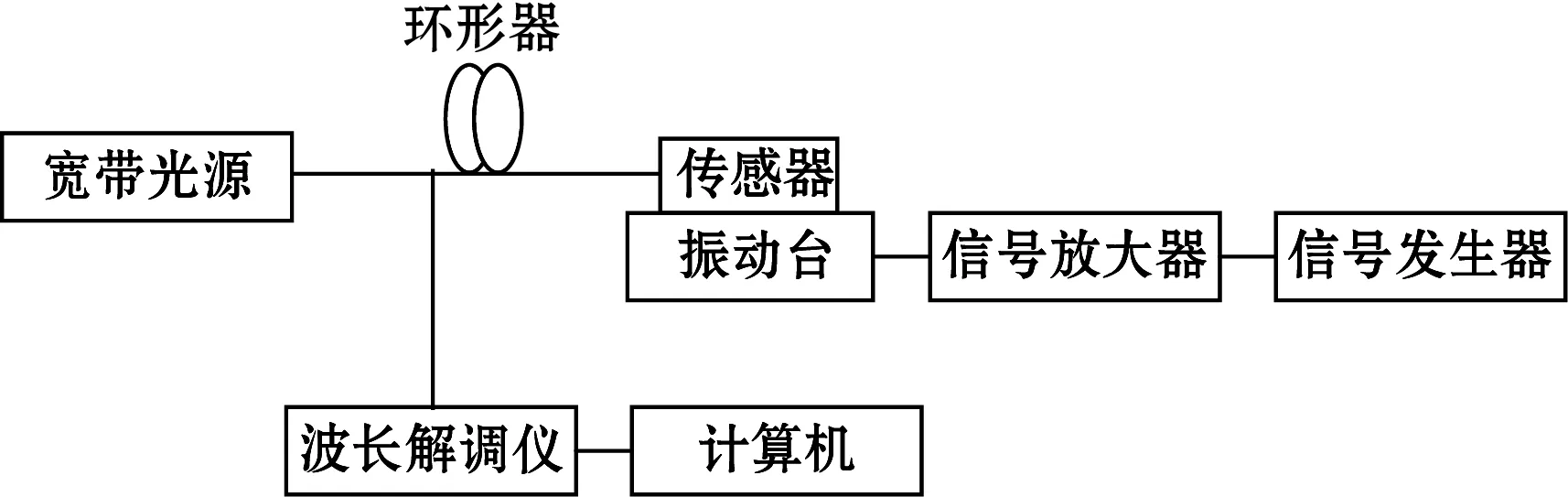
(a)示意图

(b)实物图图7 传感器灵敏度标定实验系统

3.1 响应特性分析

为测试传感器响应特性，将振动台的输出频率设置为325 Hz，加速度的输出幅值设置为1g，得到其输出频率对应光纤光栅加速度传感器响应的时域曲线，如图8所示。

图8 加速度传感器时域响应曲线

由图8可知，传感器具有良好的输出频率响应。在每一时刻，光纤光栅加速度传感器上、下两根光纤的中心波长变化量大小相等且方向相反。

3.2 灵敏度线性分析

选取325 Hz对传感器施加正弦激励信号，加速度的测试范围从0.1g增加到1.6g，步长为0.1g。测试传感器在相同正弦激励信号不同加速度下的波长漂移量，通过拟合传感器灵敏度实测值，得到传感器的灵敏度拟合曲线，如图9所示。

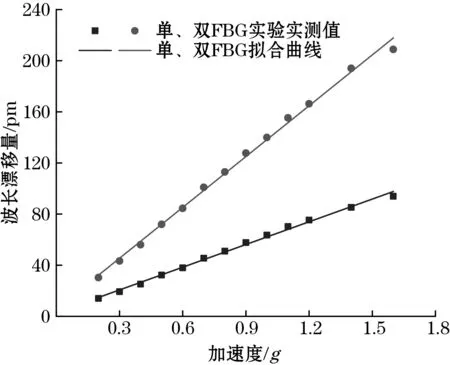
图9 灵敏度线性拟合

由图9可知，振动频率为325 Hz时，单光纤灵敏度为59.22 pm/g，拟合确定系数R2=0.995 6，经过差分运算，双光纤灵敏度为132.53 pm/g，拟合确定系数R2=0.996 2。实验结果进一步验证了双FBG加速度传感器灵敏度约等于单FBG加速度传感器灵敏度的2倍。

3.3 横向抗干扰实验

将笛卡尔坐标系套用在传感器上，则Y方向为传感器的敏感方向，而X、Z为传感器的非敏感方向。在325 Hz的振动频率，1g的加速度条件下分别测量Y方向和X、Z方向的波长漂移量，结果如图10所示。

图10 横向抗干扰实验

由图10可知，振动频率为325 Hz时，测得Y方向的波长漂移量约为140 pm，X、Z方向的波长漂移量小于4.5 pm，由此可得出传感器的横向抗干扰度小于3.3%，有利于后期制成三分量的加速度传感器。

3.4 实验结果分析

将传感器灵敏度标定实验的结果同理论灵敏度值对比，发现存在3%的误差，但已能够满足工程应用的需求。分析存在误差的原因可能为：理论分析部分采用MATLAB软件对式(4)进行线性拟合时存在误差，且进行理论计算时选取的数据都是近似值；传感器在机械加工时由于加工设备的精度不足、加工时温度不可控等原因导致椭圆铰链存在加工误差。

4 结论

本文提出了一种基于椭圆铰链的中高频双光纤光栅加速度传感器，并通过传感器灵敏度标定实验对分析优化的结果进行了分析和实验验证。实验结果表明，该传感器灵敏度为132.53 pm/g，可测频率范围为80～500 Hz，传感器的谐振频率约为780 Hz，横向抗干扰度小于3.3%。另外，实验进一步验证了双光纤差分解调法可以成倍提高传感器的灵敏度，为监测大型结构的中高频的振动提供了一种新思路。