基于承压-无压水公式的区间涌水量预测

马文奎

（佳木斯市水利勘测设计研究院，黑龙江 佳木斯 154000）

在各种矿井涌水量的计算方法中大井法是其中使用比较普遍的一个，它是以承压-无压水井公式为基础的。 但是实际的计算活动因为存在的客观地质状况及工作条件等的限制而具备了一些不确定性，而且会对计算数据的信度造成影响。 因此研究不确定因素对计算过程所造成的影响机制是十分有价值的，能够有效保障所得数据的信度。 另外，对于该类计算中不确定性的描述及信度提升等研究也变成了当前的研究热点。 其中随机数学这项方法是在地质不确定性的研究活动里中应用最为普遍的， 在该项方法中概率密度函数获取的准确性水平是实现可靠分析的关键， 但是在实际操作中因为资料的限制一般很难做到有效获取。 本文将区间不确定性角度作为出发点，同时以非概率集合理论为理论基础，一步步推导得到基于观测信息及经验公式来计算影响半径的涌水量预测公式， 而且对变量变动范围不确定状态下的涌水量区间相应作了定量描述， 从而完成了传统计算公式的转变。

1 非概率集合理论凸模型方法

式中 Ω为正定矩阵；θ为正实数。

在有界不确定参数δ=（δi）m=（δ1，δ2， …，δm）T在{δ：δTΩ δ≤θ2}集合中变动时，能够分别得到函数响应上下界的近似解公式φ=φmax及φ=φmin，即：

通过数学优化理论能够证明，在{δ：δTΩ δ≤θ2}有界凸集合范围边界上能够取得φmax及φmin的极值，设拉格朗日函数为：

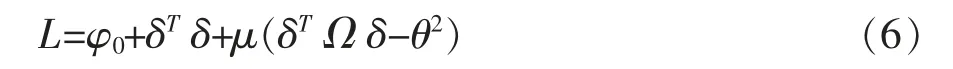
在式（6）里μ代表的是拉格朗日乘子。

取极值的必要条件是：

整理得：

把式（9）分别代入到式（4）及式（5）中能得出：

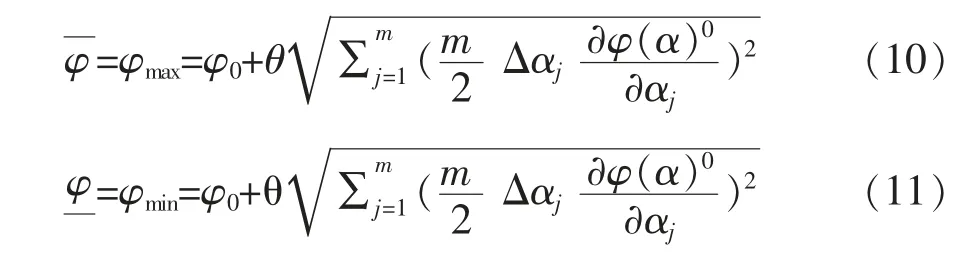
2 区间涌水量的预测公式

在各种用于地下水动力学的计算公式里， 其中一个比较重要且使用较为广泛普遍的公式是Dupuit的承压-无压水公式，其表达式在被用于涌水量计算时一般为：

式中 H0为承压含水层初始水位 （m）；Q为涌水量（m3/d）；M为含水层厚度 （m）；K为渗透系数（m/d）；rw为井的半径（m）；边界到外源水的距离（m）。

R一般使用的经验计算公式为：

式（12）的涌水量计算公式对含水层的要求是要水平等厚且质量均匀，初始的水力坡度大小是零；另外还需要具备形状为圆形的且是将抽水井作为区域中心的定水头边界，从而可以支持稳定流的形成。但实际的矿区环境中，大部分都不存在定头水边界，且很多矿区普遍具有部分陷落柱及断层，它们具有“上三带”及“下三带”，采动活动存在发生“活化”的概率。 含水层结构质量的均匀性正是由于这些具有强渗透性结构的存在而下降。所以，严格意义上的稳定流是很难在实际的矿区开采活动中形成的。 但是通过实践及研究发现， 地下含水层的水位可以在矿区的开采活动进行一定时间之后而逐渐变得越来越稳定，在这个时候可以近似默认其形成了稳定流状态。在现实操作中，通常形成的都是近似状态的稳定流，因此， 用于矿井涌水量计算的公式运行条件是近似的稳定流状态。

在整体上，式（12）中几个物理量H0，Q，M，K及rw不是线性关系。 以隐函数求导的法则为基础能够得到：

能够得到流量对变量H0、Q、M、K及rw的导数：

实际开采活动中，部分矿井能够通过观测所得数据信息及邻近矿井状况得到R， 因此并不需要基于式（13）来计算，在这种情况下的变量有5个：

把式（16）～式（24）代入式（10）与式（11）中，能够得出R0分别处2类处理状况下如表1的预测公式。

表1 区间涌水量的预测公式

表1所列的预测公式考虑到H0，Q，M，K及rw这5个变量。另外，总的变化区间范围是综合每个变量的中心值及变化率来确定的。 变量具体的平均值及变化率是基于表格中所列的表达式给出的， 涌水量的区间响应能在不借助编程的情况下快速得出。

3 涌水量预测公式的有效性

由于式（10）～式（11）是在以数学优化理论及一阶泰勒级数为基础的情况下得出的，所以对于表1中所列出的预测公式来说， 变化率的大小一定不可以表现出无界状态。 在实际操作中响应区间范围边界的确定要借助蒙特卡洛方法， 然后探究预测公式变化率界限及有效性，得到表2中的数据。

表2 不同情况下的变量变化率

表1预测公式上限值Q+和计算出的实际上限值Q这两者的相对误差即对应为表2中“最大值相对误差的绝对值”，即：

在表2中，变化率在整个计算过程中的变化规律是以固定的0.01的数距递增，从0开始增长到0.5时停止。在公式二的计算过程中，涌水量是通过式（12）运算得出的，而各组数据中的R都要通过式（13）得到的半径值扩大4倍得出， 其余参数没有发生变化。在表2中列出了各组测试数据在不同误差值大小情况下的对应变化率极值。 例如在最大值的相对误差的绝对值不超过0.05的情况下， 如果通过公式一来进行涌水量的计算，则在这种情况下式（12）的各个参数的变化率都小于0.18； 而在最大值相对误差的绝对值不超过0.1的情况下，式（12）中的各个参数的变化率都小于0.28。

如果基于同样的误差数据条件，基于表2的数据结果能够发现在这种情况下通过公式一和二得出的下限对应变量变化率是小于下限的。 这说明如果变量的变化率水平很高， 则通过公式运算得出的涌水量极小值的信度水平不如极大值。 如果要在符合一定精度需求的基础上计算出涌水量的上下限， 一个好的选择是对大区间进行分割， 在区间分割的基础上在应用表1中的计算公式。

4 实例分析

某矿井的砂岩平均厚度为33m，其含水层几乎是水平的，分布断距是接近10m的断层数条。 基于实验数据能够得知，其含水层渗透系数0.01m/d，水位标高则是+37.2m，而邻近的矿井水位标高为+38.8m。综合各种勘探孔数据信息发现， 该矿井砂岩具有并不均匀的富水性。 以该矿井所处地区的其他矿井施工信息为依据可得出， 在矿井开采活动进行一定时间之后，该类3煤层顶板砂岩含水层矿井是能够产生近似稳定的涌水量的。 该矿井的开采水平是-1010m，等效半径R是690m，首采区的形状并不规则。 首采区的涌水量在每个变量的范围区间具有不确定性时所对应的变动区间要通过公式一展开计算分析。

因为要同时考虑邻近矿井所存在的客观影响作用以及数据信息所具备的不确定性， 所以设αH0=0.05，αM=αk=αrw=0.2，水头（m）的变动范围是［985.3，1089.2］， 渗透系数 （m/d） 的变动范围是［0.008，0.012］，另外等效半径及含水层厚度（m）的变动范围分别是［552.8，829.2］及［26，39］。 而且通过计算得出涌水量的变动范围是 ［1036.9，3519.3］，Q0=2278.4m3/d是基于数据平均值计算得出的涌水量。基于上述情况能够发现，虽然各个变量在该实例中的变化率极大值只为1/5，可是涌水量的实际极值与涌水量平均值仍具有十分显著的差距，所以涌水量响应区间的分析活动是具备价值的。

图1， 图2均是为了能够更深入地对通过公式一计算得到的数据相对误差， 因变量变化率产生的变动，而呈现出具体变化规律，绘制出的数据走势图。

图1 涌水量极大值相对误差

图2 涌水量极小值相对误差

从上述两个数据走势图中能够发现， 通过公式一得出数据结果的相对误差，沿着变化率的改变，呈现出非线性变动特征。 其中通过图1能够得出，最大值的相对误差在变化率等于0.3的情况下几乎都能够保持在10%范围之内。 而通过图2能够得出，最小值的相对误差在变化率等于0.15的情况下也是几乎都能够保持在10%范围之内。 图1与图2所呈现出来的特征和表2中的数据信息是基本相同的，所以通过实例分析能够得出应用公式一来开展各个具有一定变动区间的变量所对应的涌水量的上下限的计算是比较合理的。

5 结语

总之，本文将区间不确定性角度作为出发点，同时以非概率集合理论为理论基础， 一步步推导得到基于观测信息及经验公式来计算影响半径的涌水量预测公式， 而且对变量变动范围不确定状态下的涌水量区间相应作了定量描述， 从而完成了传统计算公式的转变。 最后通过实例的具体分析发现涌水量的区间响应是能够比较便捷且具有较高信度地通过区间涌水量计算公式得出的， 区间不确定性解析公式能够提供新的可用于涌水量计算的思路方法。