基于PSO-ELM的高新技术企业财务危机预警研究

赵宝福，康馨元

（辽宁工程技术大学 工商管理学院，辽宁 葫芦岛 125105）

0 引言

中国经济实力稳步前进，高新技术企业尤其是中小型高新技术企业不断增加，2019年已经超过18万家。高新技术企业能否健康成长成为影响我国经济发展和科技创新的关键因素。高新技术企业高人力资源价值、高研发费用、高无形资产比重却伴随着资本流动性差等传统企业不存在的独特性，高新技术企业发展面临众多风险。结合高新技术企业特点建立能给企业投资者和管理者警示的财务危机预警模型，对高新技术企业实现可持续健康发展具有重要意义。

1 文献综述

财务危机预测研究主要包括预测模型构建和预测指标设定。国内外许多学者提出了不少财务预测方法：一类是基于统计理论设计方法，一类是以人工智能为代表的机器学习法。

FITZPATRICK是第一位提出单一指标财务危机预警模型的学者，其研究结果表明了在许多财务指标中最具有衡量财务危机价值的指标为产权比率和权益净利率。而后MARTIN[1]用Logistic回归分析法对企业的财务情况进行预测。以统计为基础的模型对样本的要求较高，在样本数量较大时可能出现预测效果差，泛化能力弱等情况，由此便失去了预测意义。周首华等学者成功构造出F评分财务预警模型并且在预警指标中引入现金流量指标。肖振红和杨华松[2]构造L1/2正则化的Logistic回归模型避免了财务指标之间多重共线性干扰敏感性的缺陷，提高了财务危机预警精度和模型的泛化能力。财务危机预警领域的学者在研究方法上开始引入机器学习法。LAPEDES和FARBER[3]针对银行的信用危机问题选择用神经网络法进行预警研究。李晓峰等学者基于BP财务危机预警模型可以有效衡量上市企业质量与经营业绩的同时给予上市企业财务危机警示。王小燕和姚佳含用聚类分析对财务指标相关性进行分组，用Group Bridge方法选择重要的风险指标，构造Logistic回归提出聚类Group Bridge模型。吴庆贺等[4]构建Twin-SVM模型对我国创业板上市公司不同财务状况构成的非均衡样本特性进行财务危机预警研究。周颖和张舒明[5]利用改进的等截距变换雷达图评价模型对3家*ST公司进行退市风险预警研究。张茂军等[6]研究中国制造业上市公司违约概率与财务预警指标间的关系，建立Aalen可加模型预测财务困境。郑立[7]提出针对制造业上市公司粗糙集理论融合最小二乘支持向量机的财务预警方法。周忆和张友棠用卡尔曼滤波算法构建僵尸企业财务危机动态预警模型，根据僵尸企业财务状况动态变化的特点设计了4段式僵尸企业财务危机警度判定区间。杨贵军等提出利用Benford律检验财务数据质量，建造Benford因子变量并与财务指标变量结合建造Benford-Logistic财务危机预警模型。朱发根等针对高新技术企业财务危机采用非线性SVM的方法进行预警。张晓琦运用SVM方法构建了非上市高新技术企业财务危机预警模型，证明其模型在对非上市高新技术企业财务危机预警精确度很高。耿东等构造了Logistic-BP神经网络财务预警模型，面板数据的动态预警模型不但能提高长期纵向预警能力还能多段实时预警并且其模型的预警效果良好。从这些研究中可以发现，以人工智能为代表的机器学习方法的财务危机预警模型已得到广泛关注，但目前对于财务危机预测指标的选取主要停留在纯财务指标上，非传统财务信息没有得到足够重视。针对高新技术企业财务危机预警的研究在财务指标选取上还未能完全体现出高新技术企业特点。在财务危机预警研究领域中，多数研究采用的是模糊综合评价法、Logistic回归法和BP神经网络法，但这些模型的学习时间长，学习精度不够准确，影响预测效果。

基于此，本研究在预警模型上进行了新的探索，将极限学习机（ELM）模型应用于财务危机预警中。ELM存在权值和阈值的参数随机性影响预警效果的问题，而粒子群算法（PSO）能通过寻找出最佳粒子位置来弥补ELM模型中随机解的缺陷，从而提高预警模型的精度。

2 研究方法

极限学习机（ELM），是由HUANG[8]提出对单隐层神经网络求解的快速学习方法。ELM算法的输入权重和偏置被随机赋予初始值，并且可以得出与之对应的输出权重，通过解方程组方式一次性确定。在解决训练速度慢，泛化能力差的问题上极限学习机算法具有卓越的表现，但由于输入层与中间隐含层之间映射函数的系数是随机给定的，可能会出现两个系数均为0的情况，即部分隐含层无用的情况。如果为了确保参数的合理性就需要增加隐含层节点的个数，这就导致了“过拟合”现象。为了弥补随机性的缺陷将粒子群算法优化理论对极限学习机模型进行优化。因为粒子群优化算法简单容易并且不需要做很多的参数调整，提高了算法本身的准确度。所以粒子群算法给予极限学习机更大的优势，使优化后的智能学习模型更加适合高新技术企业财务危机预警。

2.1 粒子群算法（PSO）

粒子群算法（PSO）通常用来寻找函数的最优值问题。主要是把需要优化问题的潜在解看作是P维搜索空间中的粒子。粒子均有一个v来判定飞行的距离和方向。在不停地迭代过程中，粒子们就追随个体极值Pbest和全局极值Gbest更新位置。如公式（1）-（3）。

其中，ω为惯性权重，c1和c2为加速常数，Rand()称随机函数，取值范围[0,1]。

2.2 ELM算法

ELM算法与传统神经网络算法不同点在于输入层与隐层间权值矩阵ω和隐层偏置b的处理。在传统神经网络中，国内外大多数学者通过梯度下降方法来不断地对其进行调整更新。ELM算法在众多研究领域里被广泛应用的原因之一就是它与传统神经网络相比具有“学习时间短”的独特性。因为ELM算法不需要更新ω和b，只需要在初始算法时，任意给定ω和b的值，进而计算出公式里的H。ELM模型如图1。

图1 单隐层神经网路模型图Fig.1 single hidden layer neural network model diagram

设I为隐含层个数，m为输出层神经元个数，ω是输入层与隐层间连接权值

设隐层与输出层间连接权值β为：

设隐层神经元阈值b为：

样本数据集合为：

Ω={(xi,ti)|xi∈Rn,ti∈Rm,i=1,2,…,q}，Xi=[Xi1,Xi2,…,Xin]T∈Rn表示样本具体的输入数据，期望输出结果用ti= [ti1,ti2,…,tin]T∈Rm表示。如果该网络模型的输入端数据为n，中间隐含层和输出层分别用1和m表示，则ELM的输出可以表示为：

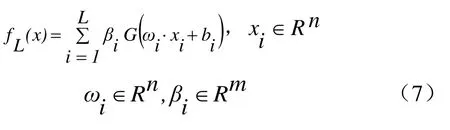
其中，

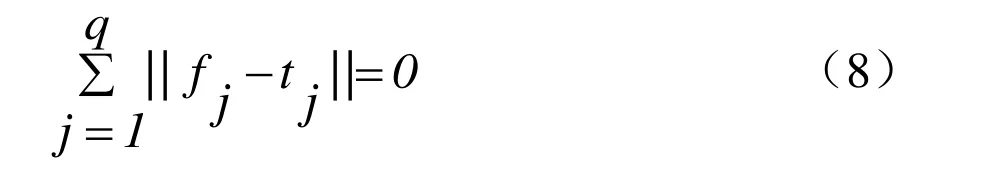
那么（7）式就可以写成：

如果模型输出与期望结果误差为0，即：

式（9）中，H是隐含层节点输出矩阵，T是期望输出矩阵。

公式（11）里，H是H+的广义逆。用正交法求得的解唯一并且最小。

目前极限学习（ELM）应用于众多领域中，比如景甜甜和洪洁[9]将PCA与ELM相结合的方法有着更高的手腕动作识别率。吴莉莉等提出的基于极限学习机的EPG波形分类识别方法具有较高的识别性能，为研发EPG波形自动识别分析系统奠定了理论基础。陆荣秀等建造GA-ELM多组含量预测方法，以此来解决稀土萃取液中有颜色特征和无颜色特征的离子共存状况下组分含量难以快速检测的问题。但目前为止，还没有将ELM算法运用到财务危机预警中，尤其是符合高新技术企业特点的财务危机预警领域中。

2.3 基于PSO-ELM的高新技术企业财务危机预警模型

ELM算法之所以训练快是因为其隐含层的权重和隐含层神经元的偏置具备随机性。若此种算法直接应用到高新技术企业财务预警研究领域中，则不利于预警的精度。因此用粒子群算法来寻找最优的权值和偏差，再结合训练速度快的极限学习机（ELM）来预警高新技术企业特点的财务危机。预警流程如图2。

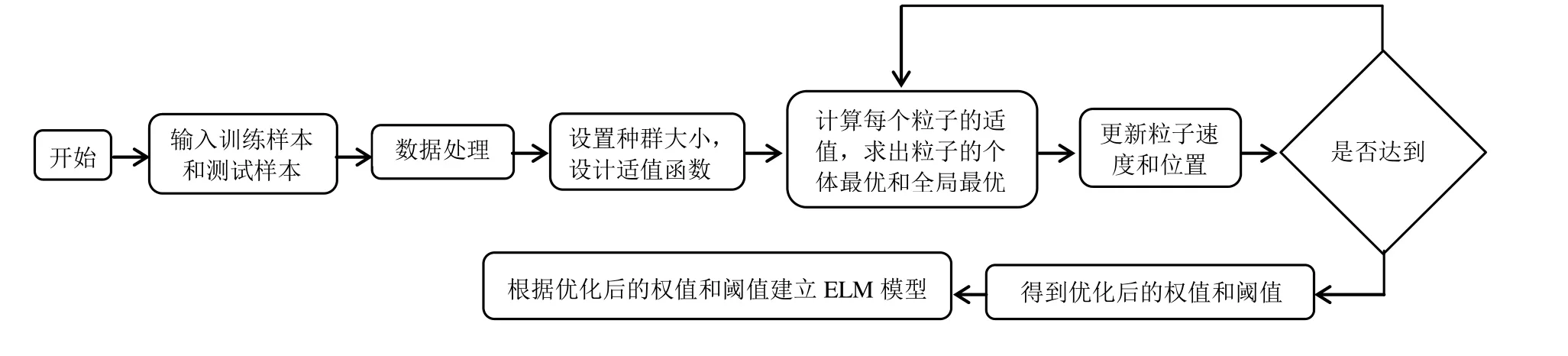
图2 粒子群优化极限学习机流程Fig.2 particle swarm optimization for extreme learning machine process

模型构建步骤如下：

指标选取：以财务危机预警为基础全面构建符合高新技术企业特点的预警指标体系。

样本的选择：选取成功在2018年或2019年被评为高新技术的企业作为样本，并查找相关财务数据。

数据处理：将数据被PSO-ELM模型训练之前，选用数据归一化方法mapminimax，将数据变成[0,1]。量值差因此被消除，确保PSO-ELM模型效果。

建立粒子群优化算法：随机给定每一个粒子的起始速度和位置，随机给定种群规模，将均方误差函数作为适应功能函数：。其中，N是数据个数，yreal期望输出值，yi模型实际预测值。多轮更新后，模型输出的值就是问题最优解。

得到最佳值：所有粒子自身经历的最佳值是根据其各自适应函数值，并从这些最佳值中确定总体最佳值。

若Present＜Pbest,Pbest=Present,Pbest=xi，否则，Pbest不变。

若Present＜gbest,gbest=Present,gbest=xi，否则，gbest。

训练ELM：优化后的连接权值和阈值就为这个问题的最优解，优化完的ELM的模型即可进行训练。

3 数据和预警指标选取

3.1 样本的选择

将高新技术企业是否被“ST”为标签来衡量是否具有财务危机。选取2018年和2019年A股主板市场高新技术企业，确保所选取样本具有一致性和可比性，剔除在2018年和2019年间退市的高新技术企业和交易状态为PT的企业，共计80个高新技术企业样本，依据 Beaver方法，采取 1:3的配对方式，即被“ST”20家，非被“ST”60家。数据来源国泰安数据库和CCER经济金融研究数据库。财务危机并非在一个时间点形成的，而是一个动态的形成过程，在t年公布被特别处理的ST企业是由其t-1年的财务数据决定的，将t-2年度作为高新技术企业的财务预警年度。

3.2 预警指标的设计

在参考国内外学者财务危机预警研究成果的基础上，结合了我国高新技术企业无形资产比重大、研发能力强等特点，从多个方面来评判高新技术企业的财务危机。在财务指标选取方面尽可能做到可靠和全面，加入了R&D投入强度、研发人员占比、新产品销售增长率等作为评判企业是否达到高新技术标准的关键指标。除了传统企业普遍适用的5大财务分析能力外还引入了股权结构和EVA，并从这7个方面初步预选出38个指标。运用SPSS中的K-S 检验和Mann-Whitney-U检验进行财务指标筛选，最终选择26个财务指标，见表1。

表1 筛选后的财务指标Tab.1 filtered financial indicators

4 结果分析

选取80家高新技术企业财务数据，随机选取60个样本作为训练集建模，实验结果如图3和图4。从对比中可以明显看出，PSO-ELM预警模型不管是训练样本还是测试样本精确率都比ELM模型更高，并且随着隐含层节点数逐渐增加PSO-ELM模型比ELM模型准确率变化幅度小，逐渐趋于稳定后精确度并无降低趋势。由此说明，在关于隐含层节点数变化方面PSO-ELM模型比ELM模型敏感性要好。PSO-ELM模型精度随着隐含层数的增加准确率逐渐增高达到100%，测试样本在隐含层节点数达到16左右，精度达到最高并且开始稳定。但ELM模型隐含层节点数为24时训练精度为80%，而且训练样本准确率与测试样本的准确率差距较大。对比可以看出，ELM模型比优化后的PSO-ELM稳健性差。因此，经过PSO算法优化的ELM财务危机预警模型不但能给高新技术企业自身提供风险评估还能给予投资人价值型参考依据。

图3 PSO-ELM模型精度Fig.3 PSO-ELM model accuracy

图4 ELM模型精度Fig.4 ELM model accuracy

鉴于目前大多数国内学者在财务危机预警领域中，所选取的人工智能方法为BP神经网络法，所以将上述相同的实验数据带入PSO-ELM模型、ELM模型和BP神经网络模型做对比实验。实验结果如表2。

表2 预测结果对比表Tab.2 comparison table of forecast results

BP神经网络、ELM模型与PSO-ELM模型的对比预测正确率分别为70%、80%和95%。PSO-ELM模型无论在训练集还是测试集，无论是否被ST的测试结果均高于BP和ELM；而未被优化过的ELM模型的正确率80%也同样高于BP神经网络模型的70%。高新技术企业可针对自身预警结果及时调整财务发展战略，也为投资者或者监管部门提供具有价值性的参考依据。

5 结论

高新技术企业是我国目前重点扶持关注的企业，研究其财务危机预警问题具有重要的现实意义。在归纳总结国内外学者有关财务危机预警研究方法和高新技术企业发展状况、国家政策的基础上，构造出满足高新技术企业独特性的财务危机智能预警模型。将高新技术企业是否被ST作为衡量财务危机的标准，结合高新技术企业特点，利用PSO对ELM模型进行优化，构建了PSO-ELM财务危机预警模型。由检测结果可知，在完全一致的训练样本的情况下，将PSO-ELM、ELM和BP三种分类模型的预测分类结果进行对比实证后发现，使用PSO-ELM模型不但预测效果较好还避免了BP神经网络出现的过度学习问题和ELM对隐含层个数的敏感性问题，凸显出PSO-ELM的稳健性和精准性。因此，粒子群优化极限学习机算法是结合高新技术企业特点评价高新技术企业财务危机的有效方法，同时PSO-ELM研究方法在其他领域中也具有一定的推广价值。