信号控制交叉口左转电动自行车交通流特性分析

钟栋青， 韦凌翔， 李 哲， 朱 军， 赵鹏飞， 廖明军,3

(1.盐城工学院 材料科学与工程学院， 江苏 盐城 224051； 2.北京建筑大学 土木与交通工程学院， 北京 102616； 3.北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室， 北京 100091)

0 引言

随着近几年电动自行车数量的快速增长，造成的交通冲突和伤亡事故也愈发严重，同时降低了车流的通行效率[1-2]. 在交叉口行驶时电动自行车具有成群性、摇摆性、膨胀性、行驶轨迹多变等特点，其中信号交叉口机动车与电动车的冲突中以左转弯最为常见[3-5]. 与传统的自行车相比，电动自行车在交叉口通行时具有流量较大时排队时间更长[6]、速度较高时安全性及稳定性较差[7]、事故率和伤亡率较高[8]、不同密度下电动自行车占用空间不同、密度较高时整体车辆的行驶速度受影响等特点[9]. 因此，研究电动自行车的安全特性及其交通流量、密度和速度的关系，对降低信号控制交叉口电动自行车的事故发生率、提高道路通行能力和安全性具有重要的意义. 对近10几年非机动车及电动自行车交通流特性研究分析如下：Lin等[10]从速度分布特性，研究比较了昆明市非机动车道上电动自行车与传统自行车交通流；Jin等[11]根据自行车道数的变化，分析不同比例电动自行车交通流的速度特性，提出一种改进的多值元胞自动机模型，模拟了电动自行车在速度较高条件下与传统自行车交通流混合行驶的运行状态；Ou等[12]在研究信号交叉口电动自行车的管理策略中发现，当进入交叉口的电动车流量增加时，直行的电动自行车增加速度要远比左转和右转的电动自行车速度高；韩宝睿等[13]调查了182组电动自行车在直行路段上的平均速度，用车道宽度和排队密度线性关系来反映密度- 流量关系；周旦等[14]调查杭州市6个非机动车道上电动自行车与自行车数据，引入了Logistic模型对车流样本中的最大速度、自由流速度、最佳密度进行了参数敏感性分析；曲昭伟等[15]基于直行电动自行车和右转机动车在6个信号交叉口中的实测数据，构建了二者位于不同释放时期的膨胀度与流量的关系模型，为交叉口组织渠化设计提供指导. 当前有关电动自行车交通流的研究大都围绕速度特性展开，并没有进行全面的分析数据流量、速度、密度之间的参数影响关系，不能系统地掌握在复杂城市交叉口环境下电动自行车的交通流特性.

本文以盐城市建军东路与开放大道交叉口左转电动自行车为研究对象，分析电动自行车流量、速度、密度的频数分布特征，分别从驶入启动期、膨胀加速期、跟随驶离期3个时期，利用最小二乘法构建左转电动自行车流量- 密度模型、流量- 速度模型以及速度- 密度模型，为提高道路通行能力，降低交通安全隐患提供参考.

1 数据来源

1.1 研究范围及原始数据获取

通过录像采集和人工计数相结合的方法获取电动自行车交通流特性的原始数据，调查研究地点为江苏省盐城市建军东路和开放大道交叉口. 调查时段选取工作日和休息日07:00—09:00、10:30—13:30、17:00—20:00，包含了高峰时段，为保证数据真实性与可靠性，共统计1 514辆左转电动自行车轨迹数据. 具体方法如下：

1)采集信号交叉口左转电动自行车的行驶视频，遵循平行四边形原则，设置视频中的测定范围为4条人行道围合的区域，并将检测区域划分为36×32格网格线，网格间距1 m；

2)根据道路交叉口的几何特征的结构，用Adobe After Effects软件在网格上虚拟三道交叉口的横截面，三道截面分别为交叉口的对角线和边线中点的连线；

3)提取轨迹点间隔为0.4 s，标定电动自行车行驶的轨迹坐标点，并转换为参数投影坐标[16].

1.2 数据处理

通过预调查发现，选取交叉口相邻两边中点的连线和对角连线，能更精准地获取车流位于不同位置时的流量、密度、速度数据和车流状态，将车流行驶方向分别划分为第1阶段(驶入启动期)、第2阶段(膨胀加速期)、第3阶段(跟随驶离期).

1) 以0.4 s为时间间隔，认定此时间间隔内电动自行车加速度与方向不变，用线性变换的方法将视频中方格网轨迹坐标转换为实际坐标，计算电动自行车相邻轨迹坐标点距离与轨迹时间间隔之比，得到每辆电动自行车分别通过3个时期的瞬时车速V，并计算所有车辆瞬时车速的平均值(km/h).

(1)

式中，V为区间平均速度(km/h)；Vi为第i辆车的瞬时速度(km/h)；n为在一定时间内观测到的车辆数(辆).

2)对交叉口东西向和南北向左转电动自行车进行流量统计，用人工计数法分别统计交叉口各相位的左转电动自行车双向流量Q(辆/h·m).

(2)

式中，q为电动自行车的流量(辆/h·m)；Q为调查时间内通过非机动车某断面的车辆数(辆)；T为调查时间(2 min)；L为电动自行车流的有效宽度(m).

3)观测某固定时间点交叉口电动自行车数量，计算车辆分布区域面积，求出车流密度K(辆/m2).

(3)

式中，K为交通流密度(辆/m2)；N为观测道路面积上的车辆总数(辆)；S为观测区域的面积(m2).

将流量、速度、密度数据按照驶入启动期、膨胀加速期、跟随驶离期3个时期进行整理、分组. 利用SPSS软件对实测数据进行回归分析，找出流量、密度、速度之间相互依赖的定量关系，分析电动自行车交通流的特性. 通过构造电动自行车左转的流量与速度、流量与密度、速度与密度的数学模型，探讨各变量的内在联系，具体数据获取图如图1所示.

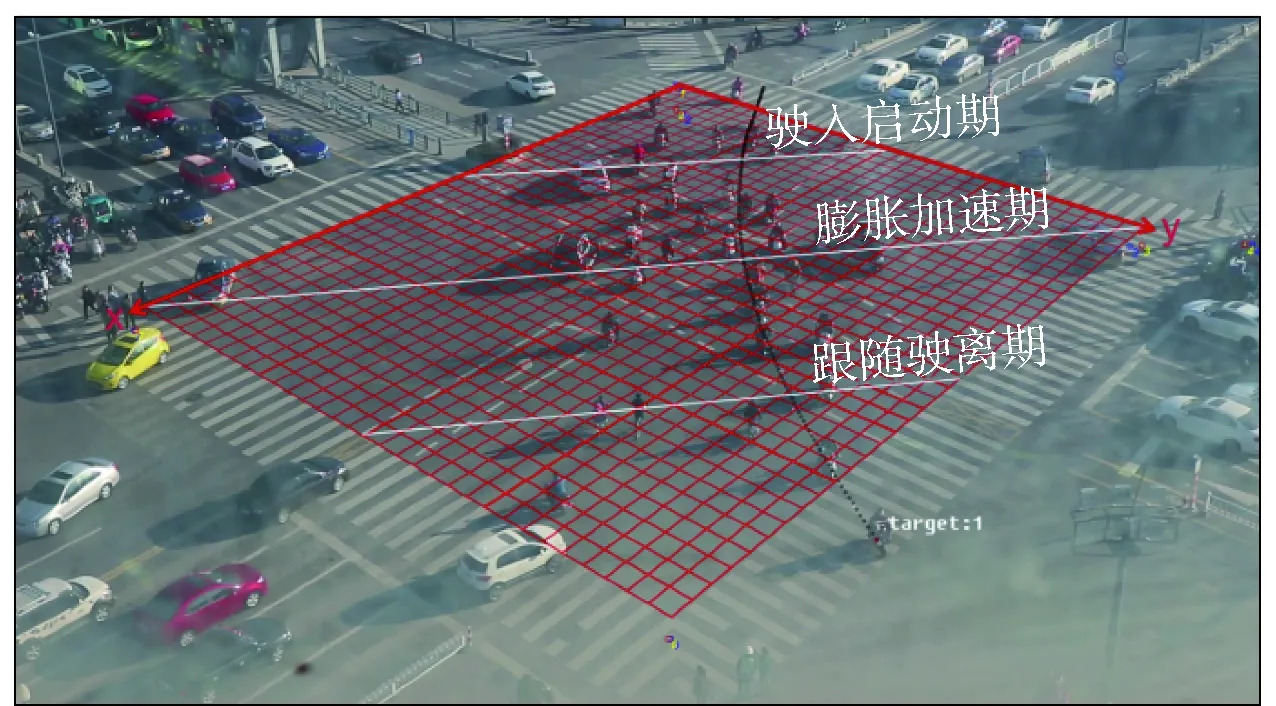
图1 数据获取图

2 电动自行车交通流总体特征

2.1 流量分析

在调查时间内分别对3个时期左转电动自行车进行计数，经过对调查地点实测数据的处理与分析，得到左转电动自行车的交通流量频数分布图如图2所示.

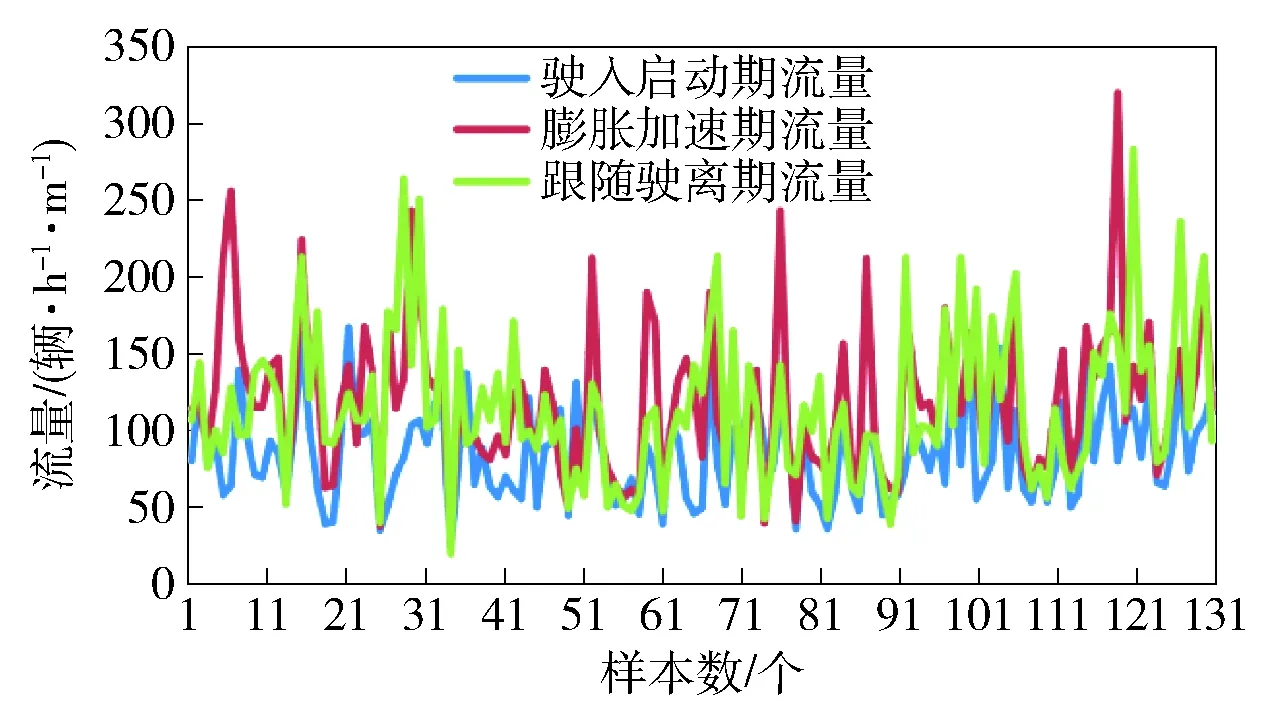
图2 左转电动自行车3个时期交通流量频数分布

可见：电动自行车通过驶入启动期时的流量最小，膨胀加速期次之，跟随驶离期最大. 3个时期的电动自行车流量主要在50～200辆/h·m之间波动，且流量没有明显的分层现象，主要原因为：车流进入驶入启动期时，车速较低，可行驶空间小，驶入启动期的车流量相对膨胀加速期、跟随驶离期较小；进入膨胀加速期时，受对向左转电动自行车流和同向左转机动车流的影响，行驶空间被压缩，车流由多辆并排行驶变成单列行驶，流量次之；进入跟随驶离期时，车流已通过交叉口的瓶颈地区，外部因素影响减弱，车流速度提高，因此跟随驶离期的车速较高，流量偏大.

2.2 速度分析

对采集的视频进行处理，识别标记电动自行车不断运动的质点位置，获取行驶轨迹坐标点；将视频图像上电动自行车的质点坐标转换为实际二维平面投影坐标，计算其行驶速度. 按照视频数据统计左转电动自行车车流分别通过3个时期瞬时车速的平均值，如图3所示.

图3 左转电动自行车3个时期交通流速度频数分布

电动自行车通过驶入启动期时的速度最小，膨胀加速期的速度次之，跟随驶离期的速度最大. 车辆通过3个时期的车速大都维持在15 km/h，此过程中速度逐渐增大，车速没有明显的分层现象，主要原因：在左转电动自行车进入驶入启动期时，车辆基本上处于启动状态，容易与同一进口道的右转机动车产生冲突[16]，在一定程度上车辆的加速进程受到影响，导致车辆整体速度偏低；车辆进入膨胀加速期，车流处于稳定流状态，车速略微提升；进入跟随驶离期，车辆行驶空间变大，车速进一步提升.

2.3 密度分析

随观测时间和左转电动自行车行驶道路面积的变化，统计在某一瞬间单位道路面积上的电动自行车数量，对调查所得的左转电动自行车的密度数据进行相应的处理得到密度分布图，见图4.

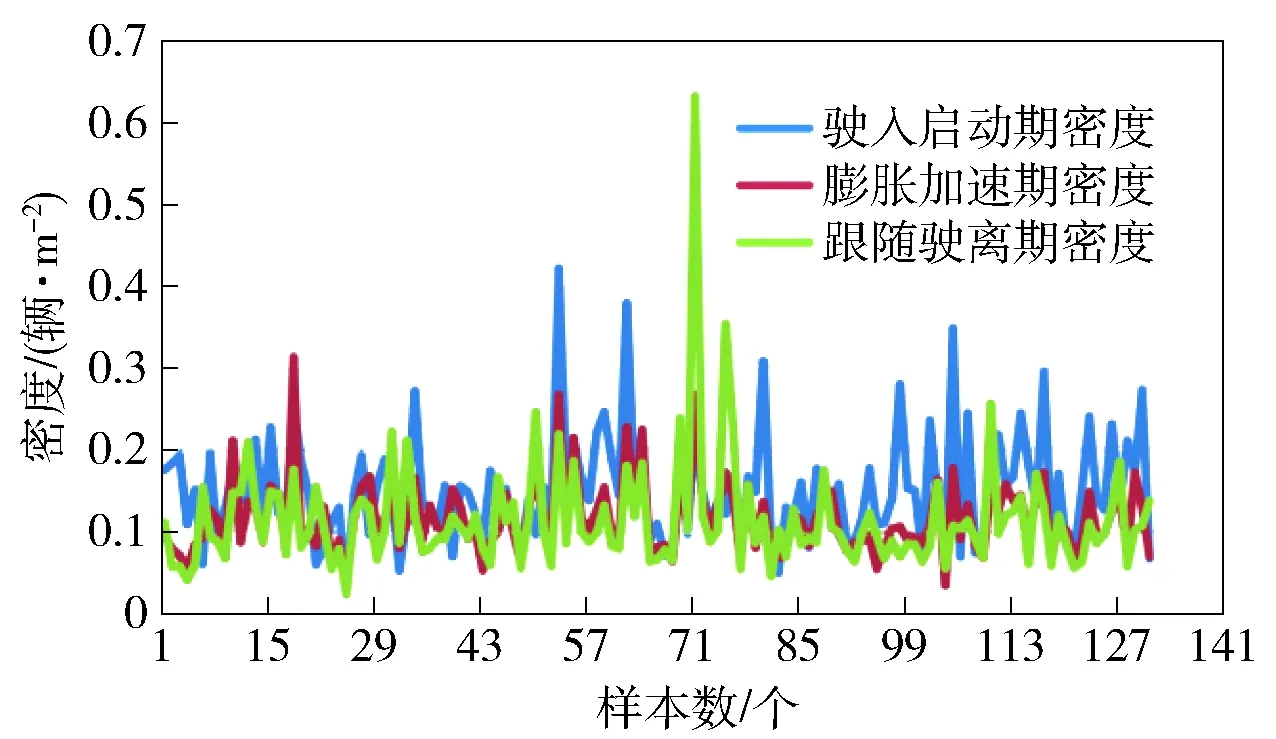
图4 左转电动自行车3个时期交通流密度频数分布

电动自行车通过驶入启动期时的车流密度普遍比膨胀加速期和跟随驶离期车流密度高，且波动性大，车流呈现膨胀性和离散性. 主要原因：进入驶入启动期时，左转电动自行车之间的间隙较小，密度较高；进入膨胀加速期时，车速逐渐提高，电动自行车的骑行范围会向行驶方向两侧扩散，车流密度降低；当车辆进入跟随驶离期时，根据电动自行车骑行者自身属性和行驶条件的不同，左转过程中车流的离散性增大，因此交通流密度偏低.

3 电动自行车交通流参数模型

3.1 流量- 密度模型分析

统计和分析左转电动自行车流量- 密度数据拟合情况，常用的拟合方法为最小二乘曲线拟合[17-20]，流量和密度之间具有显著的二次函数关系，因此建立拟合函数表达式为：

Q=D1k2+D2k+D3

(4)

式中，D1、D2、D3为回归系数；k为流量，根据实际数据拟合可得，结果如图5所示.

据与本文研究方向类似的非机动车参数模型的变量相关性文章得出[21]，在交叉口中电动自行车与机动车的交通流特性不同，其相关系数R2小于0.05属正常情况，同时也证明电动自行车在交叉口行驶时具有离散性特征.

由图5可见：当电动自行车通过驶入启动期和跟随驶离期时，左转车流密度和流量散点分布没有明显的聚集现象，R2分别为0.011 7和0.010 6，呈现出弱相关性；当车流通过膨胀加速期时，流量和密度的函数相关系数R2为0.50，呈现出显著相关，流量和密度之间存在二次函数关系. 原因分析：电动自行车流在驶入启动期和跟随驶离期时具有较高的自由度，在相同的车流量的情况下，可以多种车流密度通过交叉口；当车流进入膨胀加速期时，车流受到外部条件的影响，车辆的自由行驶的机会少，从而导致了流量和密度呈现出一定的相关性.

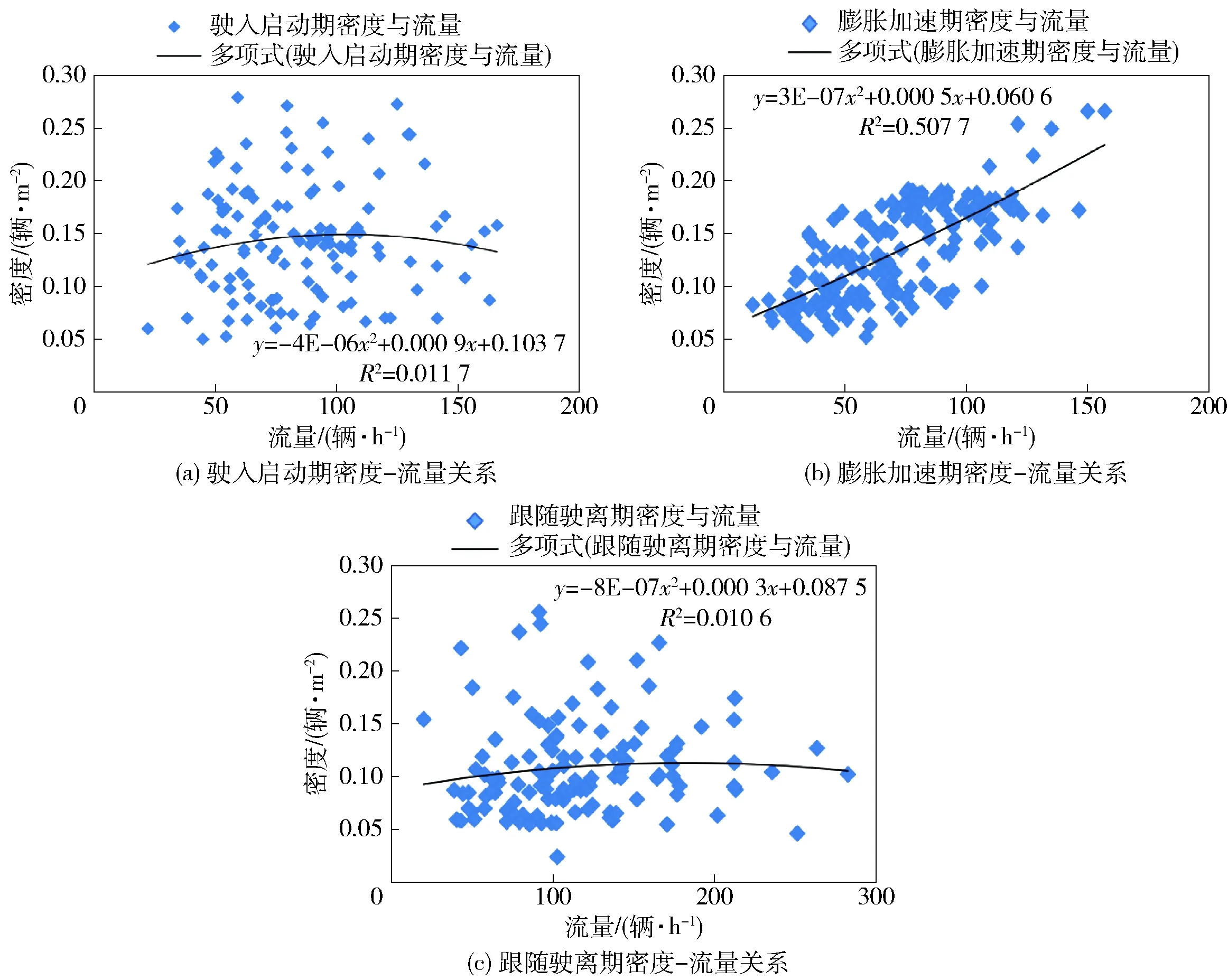
图5 3个时期密度- 流量关系

对建立的密度- 流量进行回归分析模型检验，得到模型的Sig值为0.000 12，小于0.05规定值，说明所构造的模型能较好地表达出车流流量和密度之间的内在关系. 其回归标准化残值图的整体数据偏正态分布，标准偏差为0.997,整体数据拟合度偏低，证明了电动自行车流的离散特征.

3.2 流量- 速度模型分析

统计和分析左转电动自行车3个时期的流量- 速度数据，流量与速度2个变量之间存在显著的幂函数关系，因此建立函数的数学模型为：

V=E1qE2

(5)

式中，E1、E2为回归系数；q为流量，根据实际数据拟合得到，如图6所示.

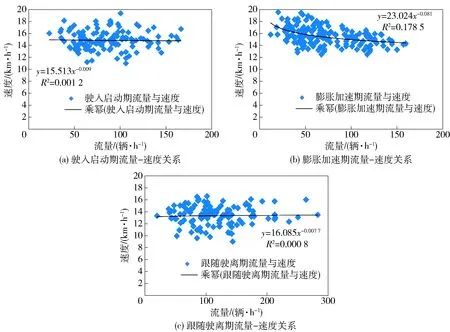
图6 3个时期流量- 速度关系

电动自行车流的车速是随着时间而逐步增长的.当电动自行车流通过驶入启动期时车流的流量与速度之间R2为0.001 2，未呈现明显的相关性；当车流进入膨胀加速期时，车流的流量与速度的R2为0.178 5，相较于驶入启动期的流量与速度关系更加显著；当车流进入跟随驶离期时，车流的流量与密度的R2为0.000 8，车流的流量与密度的相互关系逐渐减弱.原因分析：进入驶入启动期时，车辆自由行驶空间大，速度差异大，车辆处于非饱和流状态，与外界没有明显的冲突；进入膨胀加速期时，车辆处于交叉口中央，所受到的外部因素影响逐步增大；进入跟随驶离期时，车流已通过交叉口瓶颈，外部影响因素逐渐减弱.

对建立的流量- 速度模型进行统计学检验，得到的Sig值为0.000 003，小于0.05规定值，说明回归系数具有显著意义，模型构建情况良好.回归标准化残值直方图数据整体服从正态分布，标准偏差为0.997,数据整体拟合度较低.

3.3 密度- 速度模型分析

对左转电动自行车的密度与速度数据进行统计和分析，密度与速度之间的函数关系满足对数关系，因此假设拟合函数模型为：

V=F1lnK+F2

(6)

式中，F1、F2为回归系数；K为密度.根据实际数据拟合可得，如图7所示.

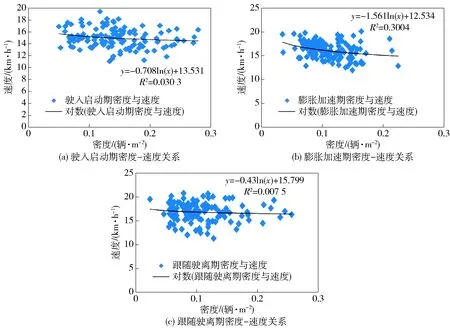
图7 3个时期密度- 速度关系

当电动自行车流通过驶入启动期时，速度与密度之间的R2为0.030 3，相关性低；当电动自行车流通过膨胀加速期时，车流的速度与密度之间的R2为0.300 4，较驶入启动期有明显的提升；当电动自行车流通过跟随驶离期时，速度与密度之间的R2为0.007 5，密度和速度没有明显的相关性；原因分析：当车流进入驶入启动期时，车辆具有较多的自由行驶空间，所受到外部因素的影响较小；在膨胀加速期所受到的影响较驶入启动期大，随着车流密度的增加速度在逐步减小，车辆处于一定的强制流状态；跟随驶离期的电动自行车拥有较高的自由度，车辆的分散程度较高，车速可在较大的范围内波动.

对建立的密度- 速度模型进行统计学检验，得到模型拟合效果的Sig值为0.000 23，小于规定的0.05，说明回归系数具有显著意义，构造的密度和速度模型良好，能较好的表达密度和速度数据之间的内在联系. 回归标准化残值直方图整体数据呈现出偏正态情况，标准偏差为0.997，拟合度较低，数据与期望线之间有较大的离散区间.

4 结束语

1)对交叉口左转电动车的流量、速度、密度3个交通流基本参数分布情况进行分析，结果表明：左转电动自行车从驶入启动期到膨胀加速期再到跟随驶离期的过程中，流量释放不均衡，速度呈上升态势，行驶区域呈膨胀性特点.

2)对交叉口左转电动车的流量、速度、密度3个交通流基本参数建立交通流参数模型，研究结果表明：流量与密度呈现二次函数关系，流量与速度呈幂函数关系，速度与密度呈对数函数关系，3种模型回归方程变量之间存在的函数关系显著，且回归系数具有显著意义.

3)本文研究结论为改善信号控制交叉口电动自行车交通安全设计提供了较为可靠的理论依据，进而可有效保证信号控制交叉口混合交通安全通行，对提高其通行能力和交通安全具有重要的意义. 另外，下一步的研究方向将聚焦不同形式的交叉口、不同转向电动自行车交通流3参数安全特性研究.