道路营运车辆卫星定位运营商绩效考评改进算法研究
2021-09-06文琰杰许旺土
文琰杰, 许旺土, 董 阳
(厦门大学建筑与土木工程学院, 厦门 361005)
0 引言
道路运输车辆卫星定位系统运营商作为政企的数据枢纽和安全生产监督者,在保障道路运输安全,提高道路客货运输效率方面起着重要的作用.
目前交通领域中管理效果评价的研究大部分集中在铁路、公路和城市公共交通系统上,涉及包括人员、经济效益、管理结构、安全性以及满意度等多个方面,但对于车辆监管定位系统评价的相关研究较少[1-3]. 道路运输车辆卫星定位系统运营商能解决政企合作关系松散性,实现主动,实时定位运输车辆的需求[4]. 针对道路运输车辆卫星定位系统运营商考评指标多维度问题,构建合理的卫星定位系统运营商考评体系,得到公平的考评结果,这对于提高政府监管效率,实现地方政府有限监管力量的优化配置,提高道路运输车辆安全具备重要意义.
目前,针对道路运输车辆卫星定位系统运营商的相关考评研究少,Xuan等[5]对企业道路运输车辆卫星定位系统评价内容、评价标准、评价标准权重展开研究,提出了层次分析法对其进行综合考评. 虽然针对道路运输车辆卫星定位系统运营商的考评研究不足,但针对不同的考评方法应用于不同的场景取得了优秀的成果,如Feng等[6]针对航空公司样本规模小、样本分布未知等问题,采用灰色关联分析法选取具有代表性的指标,并运用TOPSIS法对航空公司的排名进行排序;Zhu等[7]采用数据包络分析(DEA)方法对出租车的运营商绩效进行评估,结果表明多个DEA模型的组合可获得更为客观的效率值;张舒沁等[8]从用地、出行、经济、环境、社会5个维度选取相关指标构建了北京市TOD发展成效评价指标体系;杨国元等人[9]从旅客感知角度出发,构建了铁路客运服务质量评价体系;王玮琪等[10]提出了基于双重标准指标体系框架应用于公路建设方案必选.
综上,考评研究的核心是理解各项指标的权重关系,而获取具体评定结果时,传统方法会导致计算过程中有效信息的损失,属性识别法[11]则能对事物进行有效识别和比较分析. 属性识别法结合客观定权的方法能使得考评结果更加真实可信,张文会等[12]用熵值法计算指标权重结合属性识别模型对事故现场处置方案进行安全性评价;杨尚阳等 采用熵值法结合属性识别模型用于对路面状况的评价;郭延勇等[13]基于属性识别理论提出了高速公路安全设施综合评价模型,构建了高速公路安全设施评价指标体系. 综上,通过熵权法确定指标权重结合属性识别模型可合理地对有序数据集进行评价,但是相关论文缺少不同定权算法与属性识别模型相结合的对比.
纵览相关的研究,本文主要弥补现存研究的不足,研究内容具体如下:①提出属性识别法对道路营运车辆卫星定位运营商绩效进行评定,达到保留较多计算过程中有效中间信息的目的. ②讨论不同权重算法融合属性识别法对考评结果的影响. ③以厦门市营运车辆卫星定位运营商绩效数据为例,进行算法性能分析,验证提出算法的可行性.
1 卫星定位运营商绩效考评指标
根据交通运输部印发的《全国重点营运车辆联网联控系统考核管理办法(交运发[2016]160号)》的规定,运营商的考评指标由三大部分组成:基础硬件(BH)、技术指标(TI)、运营管理(MS). 其中每个指标都由若干个二级指标组成. 由于基础硬件与运营管理是相关管理部门的主观考察指标,也是运营商必须达标的硬性指标,其考评具备主观性和空间分布上的无差异性. 因此,本文主要以技术指标(TI)为考评内容,依照相关指标对运营商进行考评排序.
TI一共包括了5项二级指标,其内容和标称数据意义分别如下,相应指标的值标称意义一致,即其值越大则相应的考评结果越好.
1)平台连通率(PC):统计周期内,辖区内平台连通率. 低于90%为差,90%~95%为良,95%~100%为好.
2)车辆上线率(VOR):统计周期内,有营运车辆未上线(含临时报停)的扣1个百分点. 辖区内车辆上线率低于90%为差,90%~95%为良,95%~100%为好.
3)轨迹完整率(TIA):统计周期内,统计有轨迹丢失车辆占比. 辖区内车辆轨迹率低于70%为差. 70%~97%为良,97%~100%为好.
4)数据合格率(DPR):辖区内数据合格率低于80%为差,80%~90%为良,90%~100%为好.
5)卫星定位飘逸率(SPR):统计周期内,在一定时间间隔内,运输车辆的轨迹差超过阈值则认为该车轨迹出现飘逸. 辖区内卫星定位飘逸率高于5%为差,1%~5%为良,低于1%为好,为了保证数据标称的一致性对此特征进行重新定义:卫星定位非飘逸率即低于95%为差,95%~99%为良,高于99%为好.
2 融合权重的属性识别改进算法
在实际的问题中,例如考评的问题,都可归结为对定性描述的度量问题,在面对有序集方面,属性识别法与模糊综合评判法[14]得到了广泛的应用,但后者在关于回答一项数据有多“差(好)”的程度时会导致大批有用的中间信息损失,因此属性识别法具备分级清晰,关系、结论与实际相符合的优点. 考虑指标间的权重是影响属性识别法性能的关键,将提出4类融合权重算法的属性识别法改进算法融合权重算法的属性识别改进算法主要有3个核心部分:分类标准矩阵、测量数据矩阵、指标权向量.定义如下,下标i代表指标的索引,下标j为标称尺度索引,下标z为数据样本的索引,m为分类指标数,k为标称尺度数,n为样本数据条数,Ii代表第i个指标在每个评价尺度下的对应值向量,Cj代表在当前第j个尺度下各个指标的取值向量,Dz为第z条数据各项指标的测量值组成的向量,Ei为第i个指标在所有样本中的取值组成的向量.各个符号和变量的说明如下.
分类标准矩阵:
单指标分类向量:
Ii=[ai1,ai2…,aik](i=1,2,3…,m)
单分类指标向量:
测量数据矩阵:
单条数据各指标向量:
Dz=[bz1,bz2,…,bzm](z=1,2,3,…n)
单指标各条数据向量:
指标权向量:
W=[w1,w2,…,wm]
一般地,属性识别法中将各项指标认为同等重要,即各项指标权重相等.然而实际情况下各项指标的重要程度不一致,等权重法并不适用,为了使得评价结果客观合理需要充份利用已有的信息,确定各项指标的权重,即基于已有信息计算W.本节将首先介绍4类权重计算方法.
1)信息浓缩:因子分析法
因子分析法与主成分分析法类似均是利用信息浓缩的思想[15],但因子分析法通过“旋转”,让因子更具备解释意义,因子分析法通过共性因子来表达观测变量,反之,也可通过观测变量来表达共性因子,见式(1),其中Xi为观测因子,Fm为共性因子,εi为特殊因子,Fm和εi均为不可直接观测的随机变量.其矩阵形式可写为:X=AF+ε,即将m维的x变量压缩至p维.
Xi=ai1F1+ai2F2+…+aipFP+εi
(i=1,2,…,m)
(1)
2)数字相对性:层次分析法
层次分析法主要是通过专家打分获取判断矩阵,依据判断矩阵通过行(列)和求出各层指标的权重[16].其主要思想按照权重在不同层的传递来求每层各个指标的权重.特征向量归一化作为该层指标的权重向量,最大特征根用于判断判断矩阵的一致性.
3)利用数据信息量:熵值法
熵值法是依据数据携带的信息量的大小进行权重计算,熵是一种不确定性的度量,其衡量了信息的混乱程度,信息量越小,不确定性越大,熵值越大,相对应该指标获得的权重也越小[17],其核心计算流程如式(2)~(5).其中下标代表数据条的索引,一共n条数据集;下标i代表指标索引,一共m个指标,wi为第i项指标的权重.
(2)
(3)
gi=1-ei
(4)
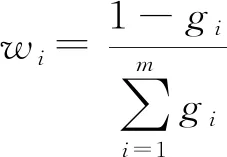
(5)
4)数据波动性:独立性权重法
独立性权重法利用多元线性回归通过计算复相关系数R进行定权,相关系数越大说明重复信息越多则权重越小,最终权重由复相关系数的倒数值进行归一化得到[18].
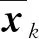
k=β0+β1x1+…+βnxm
(6)
(7)
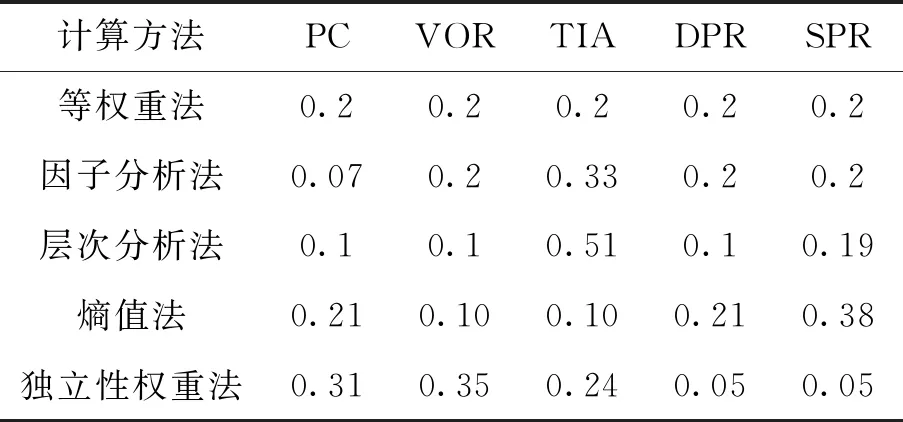
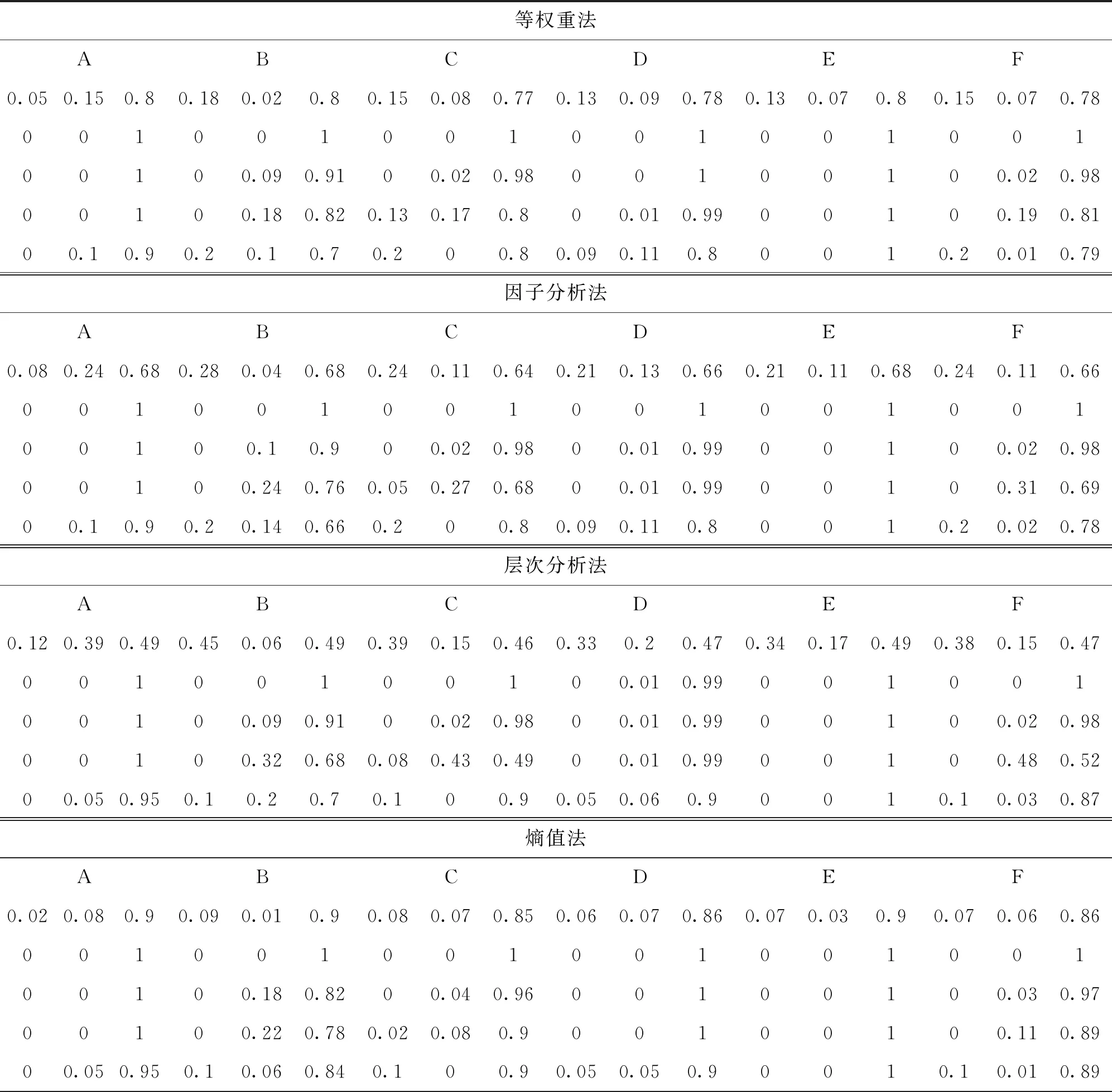
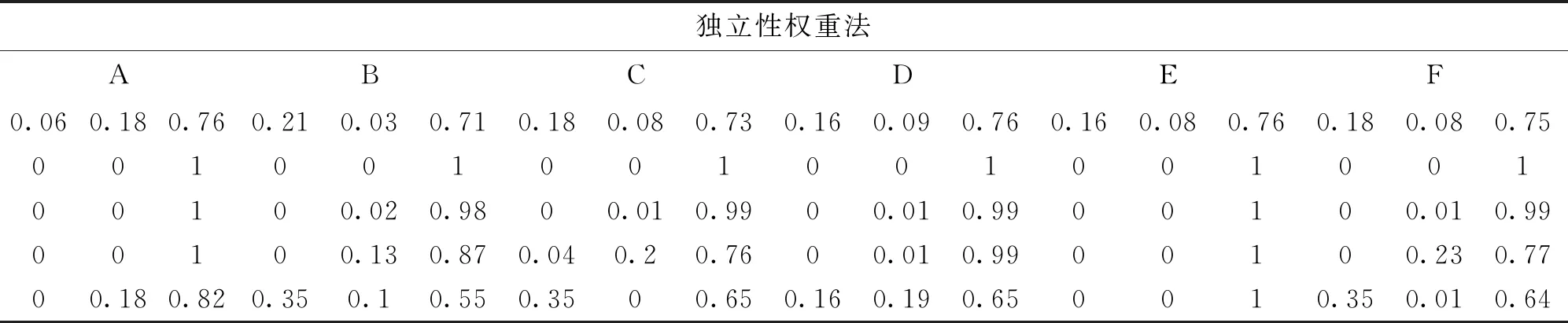
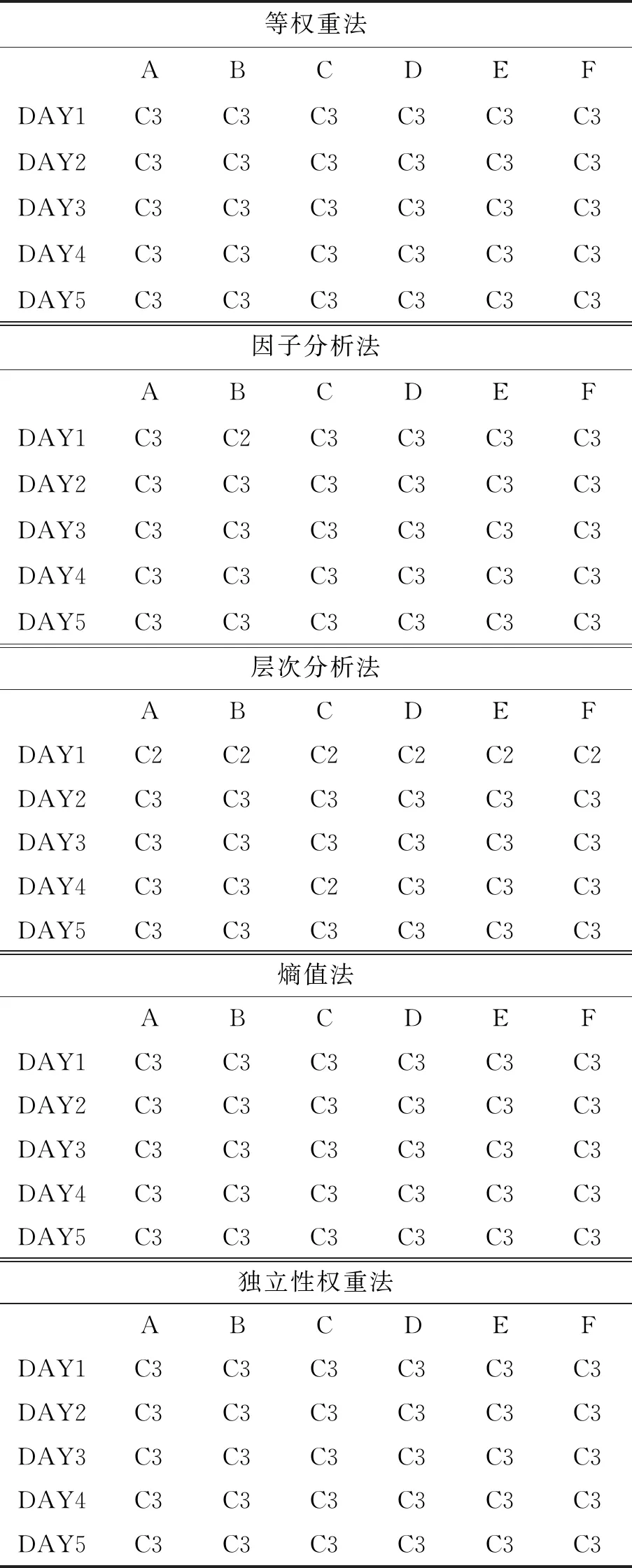
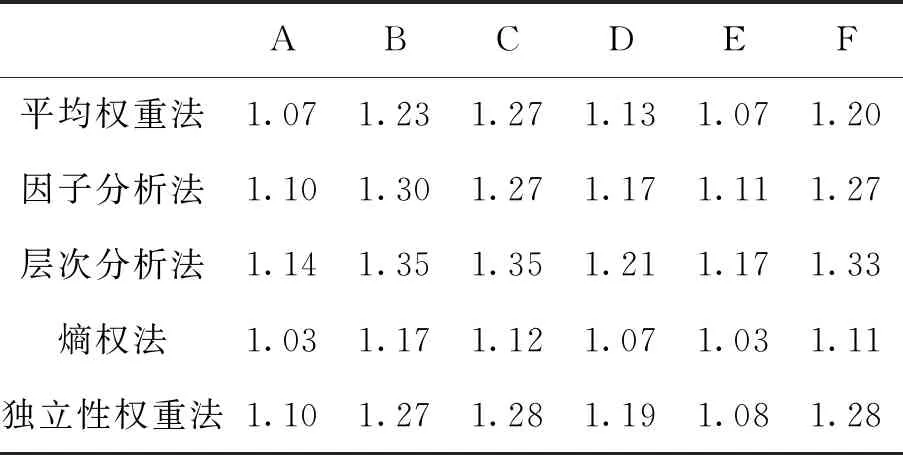
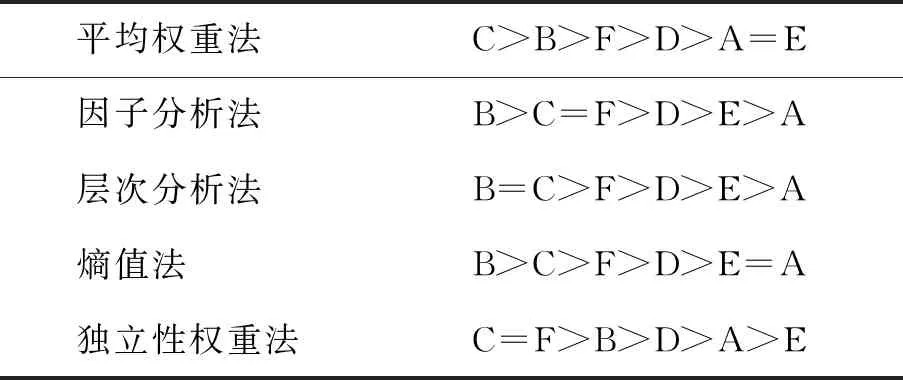
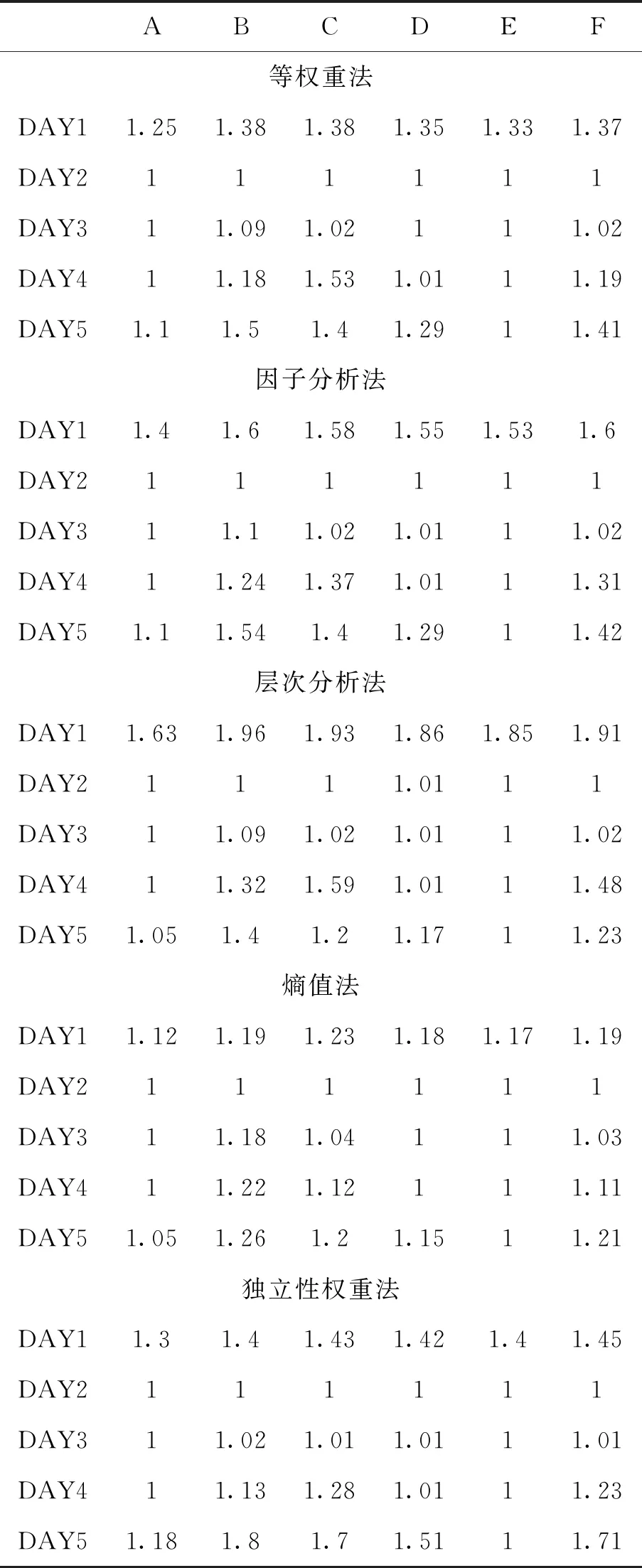
通过对核心变量的定义,结合测度函数求出测度分布矩阵,来获得考评结果,式(8)求测度分布矩阵,此处假设指标为升序,即值越大越好,满足ai1 M=BnmAmk (8) (9) 通过上述对多指标多数据条的测度计算,可得到测度分布矩阵如式(10).测度分布矩阵: (10) 基于测度矩阵需要对数据进行考评,考评准则分为基于置信度准则与基于评分标准准则.其中按照置信度准则计算式(11),取置信度为γ,lz为对应第z条数据的所属等级. (11) 按照评分标准准则计算式(12),对每条数据依据数值大小进行排序,其中sz为对应第z条数据的评分值,nj=K+1-j,1≤j≤K. (12) 按照置信度度准测可对数据样本进行等级划分,能从整体上,按照评分标准准则可在数值上动态比较数据之间的考评结果差异,能从细粒度了解数据的变化. 以厦门市06-01—06-26卫星定位运营商技术指标(TI)考评数据为基础,其中除了层次分析法不需要先验数据来获取权重外,其余3类权重计算方法均需要基于数据定权,采用06-01—06-21为获取权重数据,22—26日为实验对比数据. 基于SPSS获取各个指标的权重如表1所示,因子分析法中VOR,DPR,SPR占同等权重,TIA权重最大而PC权重最低;层次分析法依据专家经验从判断矩阵到各项指标权重,其中PC,VOR,DPR权重相等,TIA权重最大;熵值法中VOR与TIA占同等权重,PC与DPR占同等权重而SPR的权重最大,这是由于其数据分布差异性较大,熵值法缺乏各指标之间的横向比较且权值依赖于样本的原因;独立性权重中VOR、PC的权重较大而DPR与SPR的权重小,对下列不同算法的权重由大到小排序见表1. 表1 不同权重计算方法结果 由表2可看出权重算法不同其得到相应的结果也会有差异,其中因子分析法与层次分析法在数值上有所差异但在趋势上大致相同,而熵权法与独立性权重法的结果却存在较大差异. 表2 权重排序 定权后,对五日的运营商数据进行评估,其中厦门市一共6家卫星定位运营商,定义为(A,B,C,D,E,F),其分类标准矩阵如式(13),对应等级为{“差”“良”“好”}. (13) 则可获得在不同权重条件下的属性测度分布矩阵,如表3所示,其中行代表数据条,列代表对应的标称尺度.从测度矩阵看,在不同权重条件下,各运营商考评结果在“好”尺度上具备较大从属度. 表3 不同权重下运营商5日测度矩阵 续表3 表3中为对应不同权重算法结合属性识别法计算的各个运营商5日的测度矩阵,为了对在不同权重下的各个运营商进行考评结果进行考评结果比较,需要在不同的准则条件下计算其整体分级结果. 1)置信度准则 取置信度γ=0.5,根据式(10). 各运营商评分排序如表4,对应定义为{C1,C2,C3}={“差”“良”“好”}, 6家运营商5日评分等级基本为“好”,除了在以层次分析法中第1日6家运营商评分等级为“良”. 由于评分等级为离散值,能反映出运营商的整体情况,但是不能在运营商之间进行比较且分析运营商逐日的运营考评结果,因此还需按照评分标准准则进行对比. 表4 各运营商5日评分等级 2)按照评分标准准则 将测度矩阵整合为各个运营商的评分标准以数值化显示,得分越低表示考评结果越好,以此来反映单个运营商连续日的考核情况变化(见表6)以及运营商之间的考核对比情况(见表5). 由表5可对比不同权重之间各个运营商的考核情况,对其进行评分由大到小排序排序结果见表7,根据表5~ 7得到如下结论: 1)在不同权重计算方法下,运营商的考评结果也会不同(见表5),整体排序也存在差异(见表7). 表5 5日运营商平均考评得分 2)整体上A、E运营商考核情况好,而B、C运营商考核情况差(见表7). 3)独立性权重法与等权重法计算的考评结果较其他3类权重计算考评结果具备明显差异(见表7). 表7 不同权重评分大小排序 4)不同权重计算方法下,虽然得出的考评结果不同,但连续日的考评结果变化趋势基本一致(见表6). 5)以层次分析法,A运营商为例,通过连续值来表示运营商的考核情况,A运营商在第一日考核略差,而后连续3日考核较好,第5日考核略有下降(见表6),通过评分标准准则可把握运营商在不同时间段的绩效考核情况,以此达到动态监管的目的. 表6 各运营商每日考评得分情况 各指标间的权重是影响属性识别算法性能的关键,本文提出4类权重计算方法融合属性识别法并以厦门市运输车辆卫星定位系统运营商绩效考评数据为例进行算法性能实验分析,结果表明不同的权重算法下其考核的结果不相同,按照评分标准准则下运营商每日考核情况趋势一致,而在平均具体得分中,结果略有不同. 为获取指标权重,在有大批量先验数据的情况下可采用因子分析法、熵权法、独立性权重法;当无先验数据或获取数据成本较高时候可通过层次分析法确定权重. 在研究上也存在一定的不足,如数据样本量较小,因此基于小批量数据计算出来的权重具有一定的局限性,在未来的研究中可考虑融入高维度,大批量的数据进行权重的计算.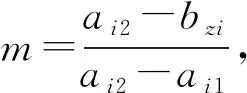
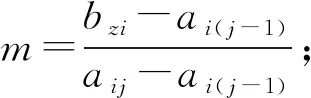
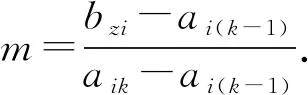
3 案例分析

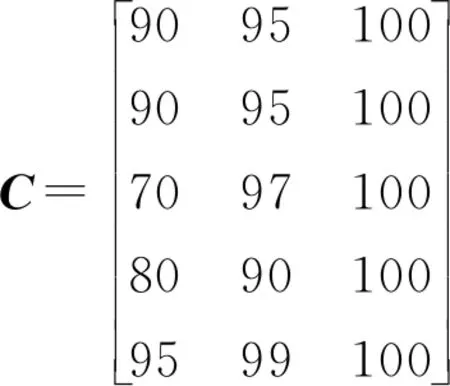
4 结束语
