十字开槽爆破片超高压爆破实验与仿真研究

2021-09-06鲁寨军姚术健范登科

工程爆破 2021年4期

鲁寨军，王灿，钟睦，姚术健，范登科

(1. 轨道交通安全教育部重点实验室，长沙 410075；2. 轨道交通安全关键技术国际合作联合实验室，长沙 410075；3. 轨道交通列车安全保障技术国家地方联合工程研究中心，长沙 410075)

爆破片具有结构简单、适应性强、经济性好的优点，作为瞬态超高压力爆破的控制阀门，具有快速的动态响应性能，压力敏感性高，能在十几毫秒迅速破裂释压，其优势远大于其他安全泄压装置，广泛应用于激波管内压缩空气的高压释能以及CO2岩土爆破等工程[1-4]。

爆破片的研究至今有90年的历史，欧美等国家先后完成了自己的爆破片技术标准制定，鲜有对外公开有价值的研究成果[5-6]。国内爆破片的研究历史相对短暂，经过40多年的发展，国内一些高等院校相继开展了一系列爆破片动态和静态工况实验研究[7-8]，其研究成果适用爆破压力在10 MPa以内的场合，主要作为压力容器的安全保护元件。涉及到超高压力爆破片瞬态爆破的研究较少，大多运用于爆破等工程上，研究对象偏向于超高压力释放对介质的作用结果[9-10]。近年一些学者关于膜片破裂失效的研究中，Kaneko等[11-13]通过加载5～15 MPa的高压氢气致使膜片破裂失效，发现当膜片厚度不变时，破裂压力随刻痕深度的减小而线性增加，并利用高速摄影成功捕捉到了膜片的开口过程。徐明等[14-15]对双脉冲发动机隔舱处金属膜片的承压、破裂过程进行数值模拟和实验验证，发现当金属膜片厚径比不变时，金属膜片破裂压强随着直径增大呈现先增大后减小再增大的规律。

目前破岩工程上使用的爆破片大多为未开槽爆破片，其破裂压力精度还有待进一步提高，会影响工程使用性能，因此研究破裂形态好、破裂压力稳定的爆破片具有积极意义。本文设计了一种十字开槽形爆破片，搭建了CO2爆破实验平台进行爆破片的爆破实验研究，并建立了十字开槽爆破片基于Johnson-Cook 损伤本构的ABAQUS有限元模型。利用实验与仿真相结合的方法，对比爆破片实验与数值仿真的破裂失效规律，验证十字开槽爆破片是否达到设计要求，并分析十字开槽爆破片的结构尺寸对破裂压力的影响。

1 十字开槽爆破片设计与爆破实验

1.1 爆破片设计

为了防止爆破片产生飞溅碎片，并保证破裂压力的稳定，本文采用在金属圆片上开诱导槽的方案，并对爆破片结构影响因素进行设计与分析。诱导槽设计成十字交叉形状，4个槽角均为90°，诱导槽沿爆破片直径方向贯通，各槽形状、槽宽、槽深均相同。主要结构参数包括直径Z、有效厚度H、槽深V、槽宽W等关键参数(见表1)，总厚度L=H+V；释放口径S为爆破片实际工作承压面的直径；开口率γ为释放口径圆面积与爆破片直径圆面积的比值，γ=S2/Z2，本文γ=0.4。爆破片的材料为Q235钢，Q235钢拥有良好的力学性能以及延展性，机械加工工艺简单，有较好的经济性和实用性。爆破片结构如图1所示。

表1 十字开槽爆破片结构参数

图1 十字开槽爆破片结构Fig.1 Structure of cruciform grooved rupture disc

1.2 实验方案

为了探究十字开槽爆破片在瞬态超高压力冲击下的动态响应过程，利用自主搭建的实验平台(见图2)进行爆破实验，实验平台包括快速增压系统、测试系统和辅助装置。快速增压系统由爆破管、信号控制器、远程控制PC端等部分组成，测试系统由压力传感器、信号采集器、信号采集PC端等部分组成，辅助装置由夹持装置、泄压装置、连接法兰等部分组成。

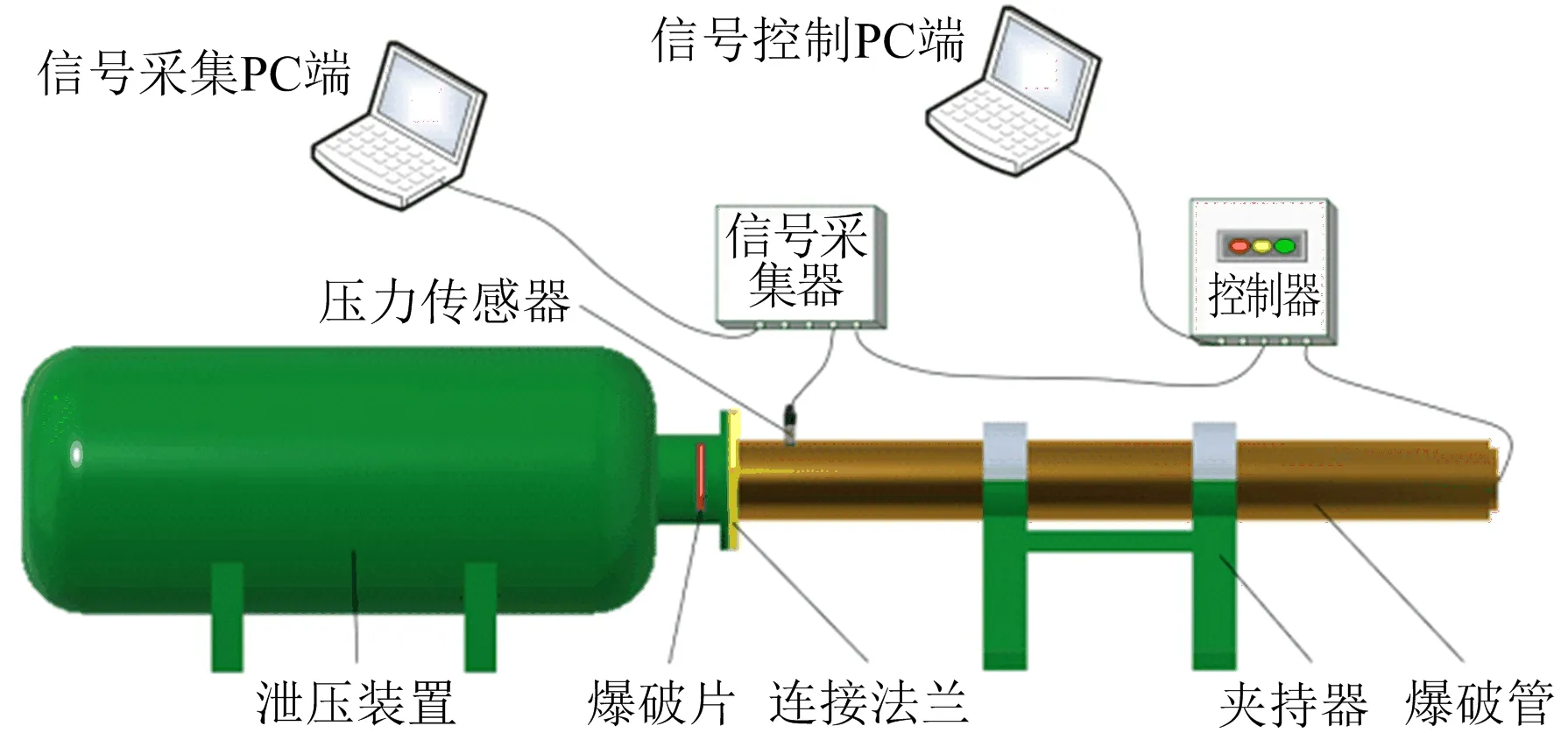
图2 CO2爆破实验平台Fig.2 CO2 blasting experiment platform

通过夹持器将爆破管固定在与泄压装置同一水平位置上，且不会发生纵向和横向位移。将十字开槽爆破片安装到爆破管内泄压端中心位置，压实并密封，保证其力学性能不会受到位置偏差的影响。爆破管右端激发线、信号采集器与控制器相连，远程控制PC端给控制器以激发信号，实现激发信号给出的同时，信号采集器同步进行采集。压力传感器安装在爆破管靠近爆破片一端位置，测量管内升压曲线。控制器给出爆破信号后，爆破管内极短时间内即可产生脉冲超高压力，爆破片受气压冲击作用失效破裂，管内压力下降。

1.2 实验结果与分析

为消除单次实验带来的结果误差，在相同条件下进行了3次重复性实验，得到3次爆破实验的压力时间曲线如图3所示。3次实验管内的压力峰值分别为72.2、69.8、71.2 MPa，升压时间分别为14、15、15 ms，3次实验的压力峰值以及时间相差较小，重复性良好。

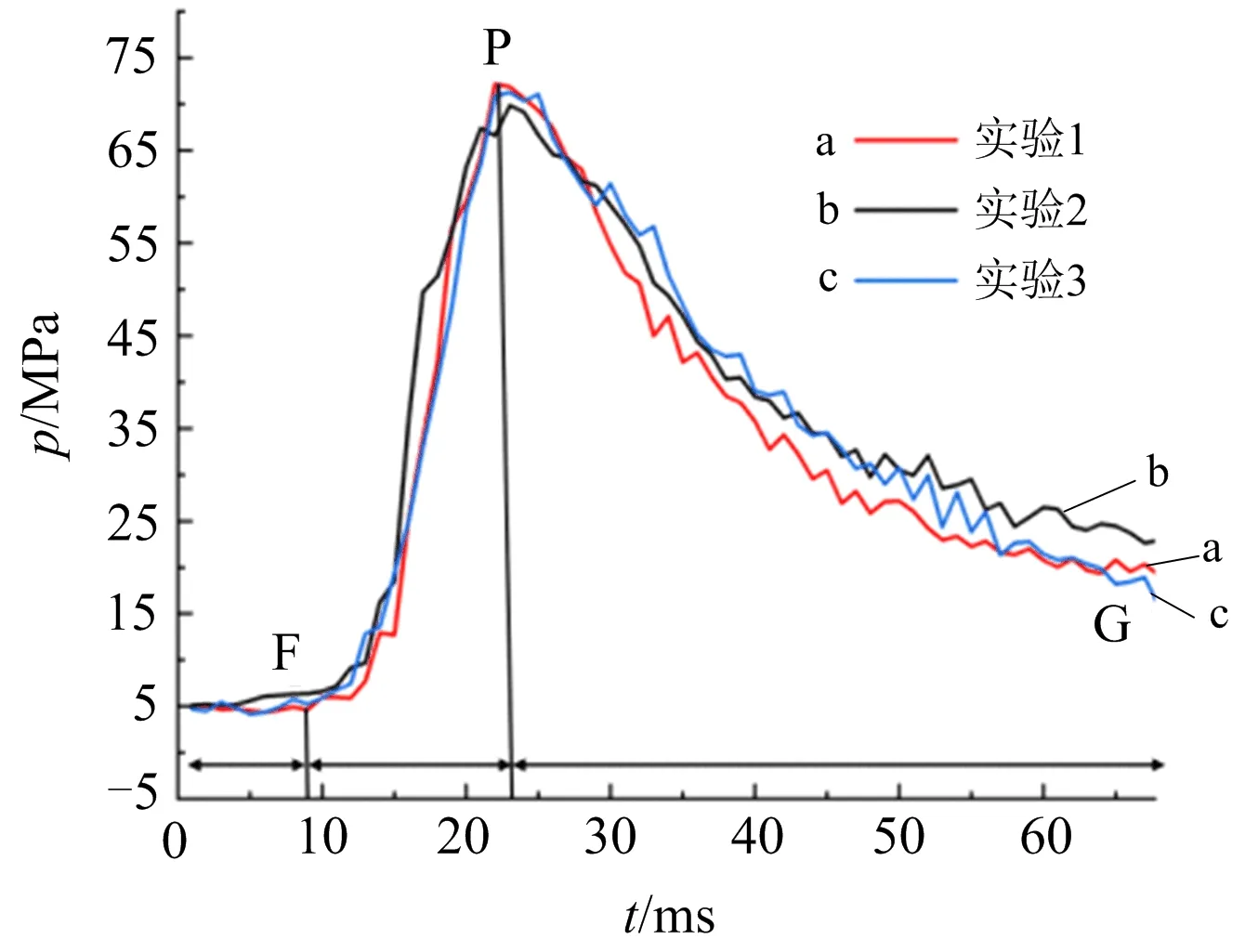
图3 3次爆破实验的压力时间Fig.3 Pressure-time of 3 blasting experiments

分析实验1爆破管内的升压曲线，从图3可以看出，整个爆破过程可以分为3个阶段。第1阶段以F点为界，在F点以前管内压力保持恒定，压力值5.1 MPa；第2阶段为FP段，管内压力短时间内急剧上升，14 ms内压力从5.1 MPa上升到72.2 MPa，爆破片受到瞬态超高气压冲击，当达到爆破片的破裂压力，爆破片破裂失效，迅速完成释压开关打开动作。P点即为实验测得的爆破片破裂压力值，也为管内泄压起始点。第3阶段为PG段，爆破管内泄压，持续时间比前两阶段长。

十字开槽爆破片受到瞬态冲击载荷作用，达到材料的屈服强度后，开始产生塑性变形，爆破片受力拉伸膨胀。当达到极限强度后，十字诱导槽中心开始出现裂纹，各瓣产生外拱变形，裂纹从诱导槽中心沿边缘持续扩展，最终开裂成瓣。十字开槽爆破片的破裂失效形态如图4所示，3次重复实验的破裂形态基本一致，每一片的四瓣均由内向外呈一定弧度凸起，每两个相邻瓣之间呈45°。各瓣开口拱起高度接近一致，实验1中爆破片瓣平均开口高度为22.1 mm，开口的垂直投影几何形状接近于正方形，通过图像处理分析，得到开口面积为10.5 cm2，占整个承压面积的75.6 %，开口有效面积利用率较高，且不会产生飞溅碎片。

图4 十字开槽爆破片破裂失效形态Fig.4 Cruciform grooved rupture disc rupture failure shape

2 十字开槽爆破片模型及验证

2.1 计算模型

建立十字开槽爆破片的有限元单元模型，利用ABAQUS 有限元仿真软件求解计算。为了减少模型工作计算量，对仿真模型进行简化处理，爆破片上下夹持装置采用刚体薄壳单元代替，并在刚体薄壳边界加以固定约束，爆破片与刚体薄壳之间设置摩擦接触。爆破片使用六面体八节点单元(C3D8R)进行离散(见图5)，为消除单元尺寸对计算结果的影响，爆破片中心域分别采用了0.3、0.5、0.7 mm单元尺寸进行离散，其他区域单元尺寸为1 mm。

图5 十字开槽爆破片有限元计算模型Fig.5 Finite element calculation model of cruciform grooved rupture disc

Johnson-Cook模型是描述金属或合金应变率断裂损伤的经验本构模型，认为材料的屈服流变应力主要受其应变硬化、应变率效应以及温度软化效应影响[16]。根据Johnson-Cook模型描述，材料的流动应力公式为

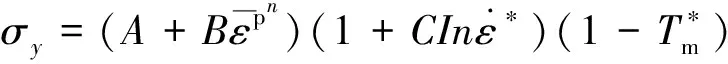
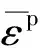
Q235钢J-C本构模型参数[17-19]如表2所示。

表2 Q235钢 J-C本构模型参数

式中：D1～D5为断裂应变常数;σ*=σn/σe为应力三轴度;σn为静水压;σe为Mises等效应力。

Q235钢J-C模型断裂失效模型参数如表3所示[20]。

表3 Q235钢 J-C 断裂失效模型参数

2.2 模型验证

对实验1的十字开槽爆破片动态破裂失效过程进行了仿真分析，由3种中心域网格尺寸仿真模型的计算结果(见表4)可以看出，当中心域网格尺寸为0.3 mm时，仿真相对于实验的破裂压力误差为4.7%，破裂时间误差为3.4%，计算已具有较高精度。中心域网格尺寸为0.3 mm和0.7 mm的仿真计算破裂压力值相差仅为0.9 MPa，在工程误差允许范围内。

表4 仿真与实验1结果对比

应力形变云图能更加直观地反映十字开槽爆破片整个破裂失效过程。由中心域网格尺寸为0.3 mm的爆破片模型随时间变化的形貌(见图6)可知，爆破片达到屈服应力之前，最大应力主要集中在十字槽角和释放口径边缘位置。当承压区域突破屈服极限，十字槽中心区域开始产生较大变形，应力逐渐增大。在t=6.1～12.9 ms区间内，随着时间的增长，最大应力从十字槽中心区域逐渐向四周扩展，开槽面向外胀起程度加深；当t=13.5 ms时，网格应变达到1.52，十字槽中心域开始出现裂纹，出现在靠近直角槽位置(此处为应力集中点)，破裂失效前的最大应力为678 MPa。裂纹随着槽径向四周扩展，承压面裂开成四瓣，每一瓣在压力持续作用下向外翻转，当t=13.7 ms时，达到最大垂直拱高(21.8 mm)，与实验相差仅为1.4%。每条槽断裂之后，相邻断裂面开口接近45°，与实验结果吻合度高。爆破片出现裂纹开始到释放口完全张开的时间少于0.2 ms，验证了所设计的十字开槽爆破片能在瞬间实现开口释压动作。

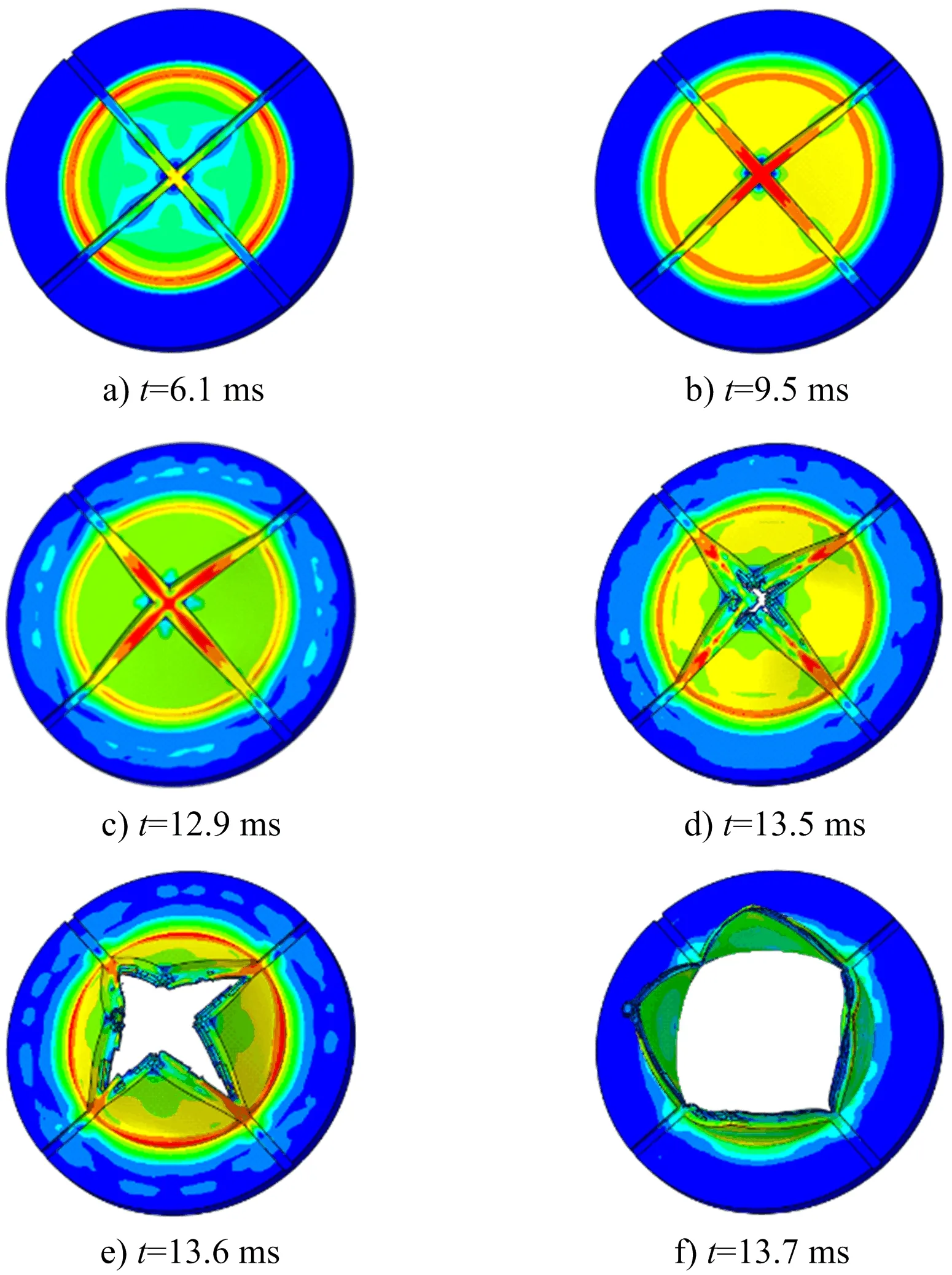
图6 十字开槽爆破片不同时刻的应变云图Fig.6 Strain cloud of cruciform grooved rupture disc at different moments

3 爆破片破裂压力影响因素分析

为了确定爆破片的设计方案，需要对不同厚度、槽深、槽宽等影响因素进行分析。在已有实验与仿真的基础上，针对直径为66 mm、开口率为0.4的十字开槽爆破片，设计一系列不同尺寸的爆破片进行仿真研究。在承压面施加线性增加载荷，并根据仿真计算结果，拟合各因素与破裂压力之间的关系(见图7)。

图7 破裂压力随结构参数的变化关系Fig.7 Relationship of rupture pressure and structural parameters

保持十字开槽爆破片的槽深1.5 mm和槽宽2 mm不变，只改变爆破片的有效厚度，得到破裂压力随有效厚度变化的拟合曲线(见图7a)。可以看出，破裂压力与有效厚度成明显的线性比例关系，当有效厚度从1 mm增大到3 mm时，破裂压力随有效厚度增大而显著上升，从32.1 MPa增大到了110.2 MPa。

保持十字开槽爆破片的有效厚度2 mm和槽宽2 mm不变，改变槽深(总厚度随之改变)，得到破裂压力随槽深变化的拟合曲线(见图7b)。可以看出，当槽深小于1.3 mm时，破裂压力随着槽深的增大而下降；槽深为1.3 mm时，破裂压力最小；当槽深大于1.3 mm后，破裂压力随着槽深增大而上升。有效厚度一定，槽深增加则总厚度增加，未开槽的区域承载能力也随之增加。但当槽深小于1.3 mm时，随着槽深的增加，尽管总厚度增加在一定程度上增加了未开槽区域的承载能力，但十字槽角位置也越容易产生应力集中(见图8)。应力集中导致开槽位置承载能力下降的幅度大于总厚度增加带来的承载能力增加的幅度，因此破裂压力反而越小；若爆破片不加工诱导槽，理论破裂压力将会达到最大。当槽深为1.3 mm时，应力集中导致开槽位置承载能力下降的幅度与总厚度增加带来的承载能力增加的幅度相当，破裂压力达到最小值。当槽深大于1.3 mm后，爆破片总厚度对破裂压力的影响逐渐增大，应力集中带来的不利影响小于总厚度增加导致的强度提升。由图7b可见，槽深在1 ～1.5 mm之间时，压力变化范围最小，相对释压稳定性好。

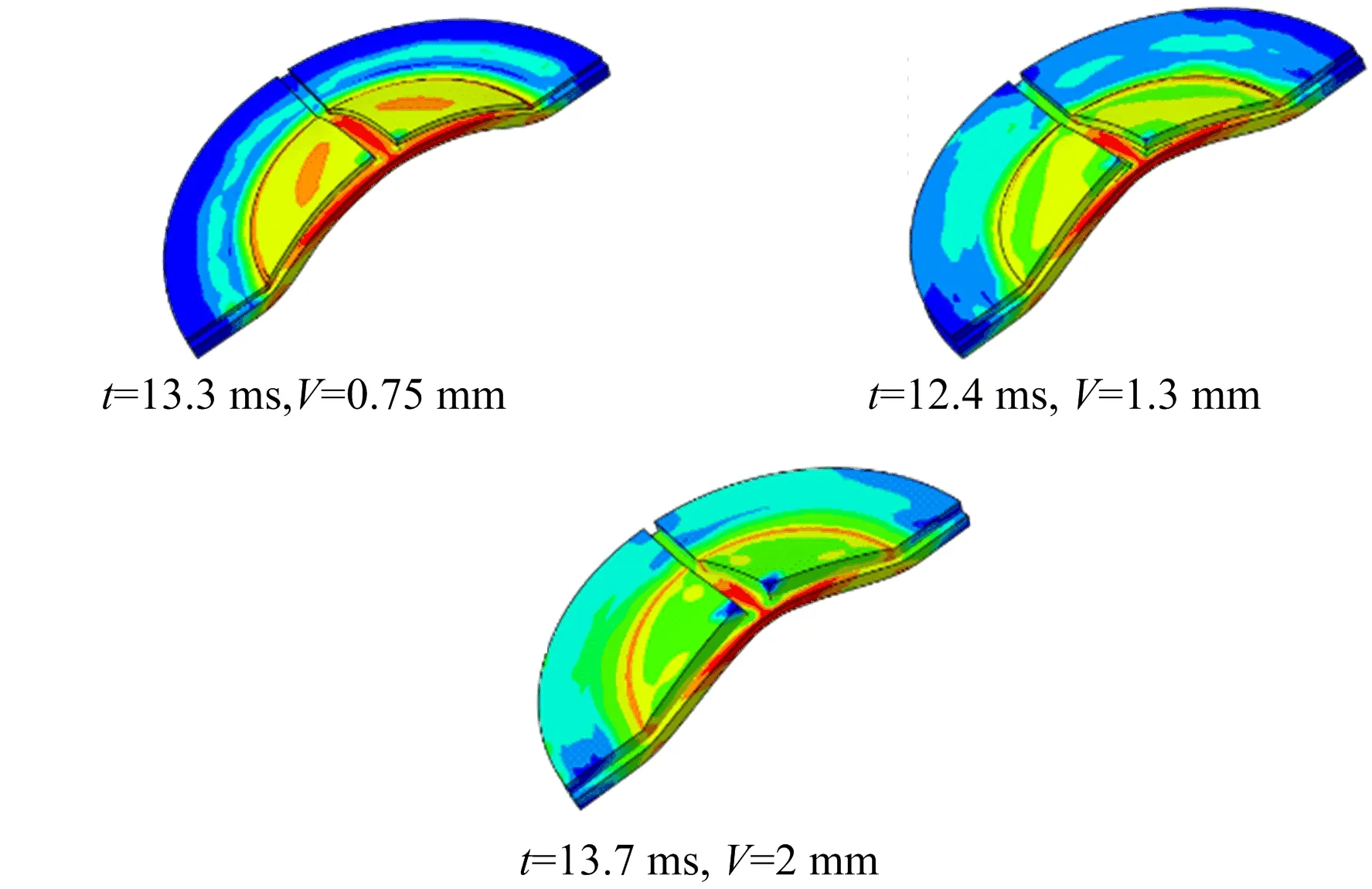
图8 不同槽深情况下中心域应力最大时刻云图Fig.8 Cloud at the moment of maximum stress in central domain under different groove depths

保持十字开槽爆破片的有效厚度2 mm和槽深1.5 mm不变，改变槽宽，得到破裂压力随槽宽变化的拟合曲线(见图7c)，可知破裂压力与槽宽之间成指数函数关系，并在图中给出了拟合关系式。当槽宽小于4 mm时，随着槽宽的增大，十字槽中心区域拉伸变形增大，爆破片产生断裂应变的时间也相应增加(见图9)，破裂压力随之增大；当槽宽达到4 mm以后，诱导槽宽度对破裂压力的影响作用下降，槽宽与破裂压力曲线上升逐渐平缓。

图9 不同槽宽情况下出现裂纹时刻的应变云图Fig.9 Strain cloud at the moment of cracks under different groove widths

综上所述，十字开槽爆破片破裂压力随有效厚度变化的拟合曲线斜率为39.1 MPa/mm，随槽深变化的拟合曲线斜率最大在槽深1.5～2 mm区间段，为14.7 MPa/mm，随槽宽变化的拟合曲线斜率最大在槽宽1～3 mm区间段，为5.2 MPa/mm。破裂压力随有效厚度变化拟合曲线的上升梯度远大于槽深和槽宽。因此，十字开槽爆破片的有效厚度是影响破裂压力的最重要因素。