火灾条件下冷弯薄壁型钢楼板体系的耐火性能

2021-09-06杨成罗浪宋谦益

土木与环境工程学报 2021年5期

杨成，罗浪，宋谦益

(1.西南交通大学 a.陆地交通地质灾害防治技术国家工程实验室；b.土木工程学院,成都 610031；2.中国建筑西南设计研究院有限公司，成都 610041)

冷弯薄壁型钢结构作为一种装配式钢结构，主要通过自攻螺钉将冷弯薄壁型钢骨架连接成框架，并在框架一侧或两侧覆以结构板材形成墙体、楼板等受力构件。并在结构构件基体外再覆以石膏板、玻镁板等具备防火、隔声、装饰等性能的建筑板材，以满足建筑结构的功能性需求。钢结构在高温下的强度和刚度衰退非常显著[1-2]，冷弯薄壁型钢楼板作为该结构体系中重要的承重结构构件，其耐火性能得到日益关注[3-5]。

其他国家开展冷弯薄壁型钢结构火灾试验研究[6-8]已积累了一定的经验和数据，而中国的试验研究[9-11]相对有限。相比火灾试验耗资大、耗时长，数值分析提供了更便捷的方式以了解其在火灾下的温度分布[12-15]和结构性能[16]。Keerthan等[17]利用SAFIR进行了冷弯薄壁型钢墙体的二维瞬态传热模拟。Feng等[12]利用ABAQUS对冷弯薄壁型钢墙体截面建立了二维传热模型。Baleshan等[18]和Jatheeshan等[19]使用简化的线性温度分布对火灾下冷弯薄壁型钢托梁的结构行为进行了模拟。

1 三维传热模型

1.1 模型的建立

以Baleshan等[8]的试件为分析对象，利用有限元分析平台ABAQUS建立两个2 400 mm×2 100 mm(长×宽)的冷弯薄壁型钢楼板模型，包括4根钢托梁和两根导轨组成的钢骨架以及受火侧、背火侧板材。所用冷弯薄壁型钢的钢材等级为G500，采用C型截面钢(托梁C180 mm×40 mm×15 mm×1.15 mm，腹板高度h×翼缘宽度b×卷边宽度a×厚度t)及U型截面钢(导轨U182 mm×50 mm×1.15 mm，h×b×t)，钢托梁(J1、J2、J3、J4)之间间距S均为600 mm。试件沿截面厚度方向的板材组合和钢托梁布置如图1所示。

图1 试件构造示意图

值得注意的是，试件在受火侧空腔面设有3个200 mm宽的石膏板背挡块，如图2(a)所示。此处空腔形状已发生改变，结构沿跨度方向温度分布不均匀，故二维截面传热模型不再适用[22]。

传热分析数值模拟中，石膏板、岩棉和胶合板采用8节点三维实体传热单元(DC3D8)，冷弯薄壁型钢骨架采用4节点壳体传热单元(DS4)。根据敏感性分析结果，选择模型平面网格密度为80 mm，在钢骨架与板材相交区域网格细化为10 mm；厚度方向网格密度为5 mm，它决定了板材厚度方向的传热情况，因此，在此方向采用更细的网格划分，如图2(b)所示。

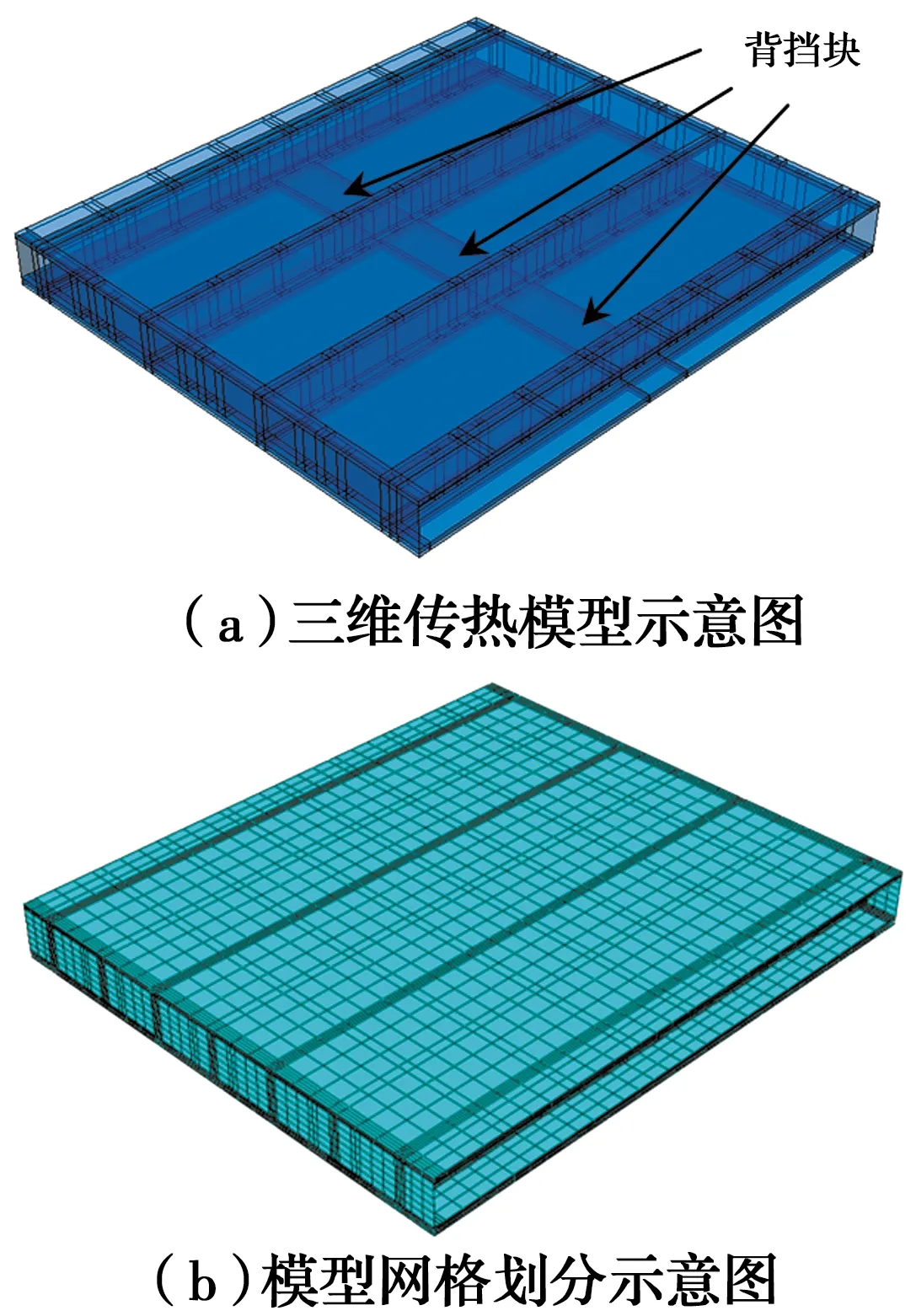
图2 冷弯薄壁型钢楼板模型示意图(试件1)

在试验开始前，以增量的方式给楼板试件背火侧施压至荷载比0.4，然后受火侧开始升温，直至结构丧失耐火承载力。试件1的耐火极限时间为107 min，试件2为139 min。试验后，观察结果发现：试件1受火侧石膏板有烧蚀、脱落的现象，其背火侧胶合板在空腔侧形成烧焦层，其他表面状况良好，基本保持了背火侧板材的完整性。试件2受火侧岩棉发生收缩，导致接缝的开放和内侧石膏板层的暴露、烧蚀及脱落。

图3 测温点位置(图中红点)示意图

1.2 边界条件

由于实际楼板体系中钢骨架与两侧板材以及各板材之间接触非常紧密，故对其相交部分定义为绑定连接，以确保它们之间的固体传热。

在分析过程中，受火侧的火灾升温曲线是根据ISO-834标准升温曲线[21]确定的，同时考虑环境温度为20 ℃。Stefan-Boltzmann常数取5.668×10-8W/m2/℃4，既有研究对于热对流系数和热辐射系数的取值见表1，彼此之间没有显著差异。参考Song等[23-24]的研究，受火侧对流系数与辐射系数分别取25 W/(m2·℃)和0.9；背火侧分别取10 W/(m2·℃)和0.7。模型空腔内均未填充隔热材料，因此，腔体内部表面设置空腔辐射系数，取值0.7，如图4所示。

表1 既有文献的热边界条件取值

图4 三维传热模型的边界条件

1.3 材料热工参数的确定

选取高温下石膏板、岩棉、胶合板与冷弯薄壁型钢合适的热工参数(如：导热系数、比热容和相对密度)是传热分析的关键。石膏板的热工参数主要受到内部化学成分、烧蚀以及含水率的影响，为此分别采用Keerthan等[17]提出的高温下石膏板的导热系数、相对密度及Feng等[12]提出的比热容。岩棉比热容和密度在高温下变化不大，采用Jatheeshan等[26]的取值，其导热系数则采用Sterner等[27]的数据。胶合板和钢材的热工参数分别按照Jatheeshan等[26]和BS EN 1993-1-2[28]的建议取值。

1.3.1 石膏板根据已有试验结果[12-14, 17]，选取合适的石膏板热工参数进行传热模拟。石膏板在火灾影响下煅烧收缩形成小裂缝后部分脱落。这将导致更多的热量通过楼板腔体，故选用参数[17]考虑了1 000 ℃后石膏板开裂造成导热系数增大的影响，如图5所示。

图5 石膏板导热系数曲线

图6显示了使用的石膏板比热变化曲线。在100 ℃时，石膏板内部结合水吸热蒸发，温度上升将会有一个延迟，这会显著影响石膏板的比热。在125 ℃时，石膏板比热达到峰值24 572.32 J/(kg·℃)[12]。

图6 石膏板比热容曲线

图7为使用的石膏板的相对密度曲线。125～175 ℃时，石膏板因高温产生的质量损失为10%，在接下来的火灾过程中，其密度保持不变[17]。

图7 石膏板相对密度曲线

1.3.2 岩棉图8给出了几种既有的岩棉导热系数曲线[15, 17, 27, 29]。各地岩棉的化学成分有所不同，热性能略有差异，但其导热系数均随温度的升高而上升。在分析中，岩棉比热容采用定值840 J/(kg·℃)，密度恒为100 kg/m3[26]。

图8 岩棉导热系数曲线

1.3.3 钢材钢材的导热系数和比热容依据欧洲规范BS EN 1993-1-2[28]的建议公式取值，该公式考虑了钢材在735 ℃时比热容出现峰值的现象，如图9、图10所示。在整个火灾过程中，钢材的密度保持7 850 kg/m3不变[26]。

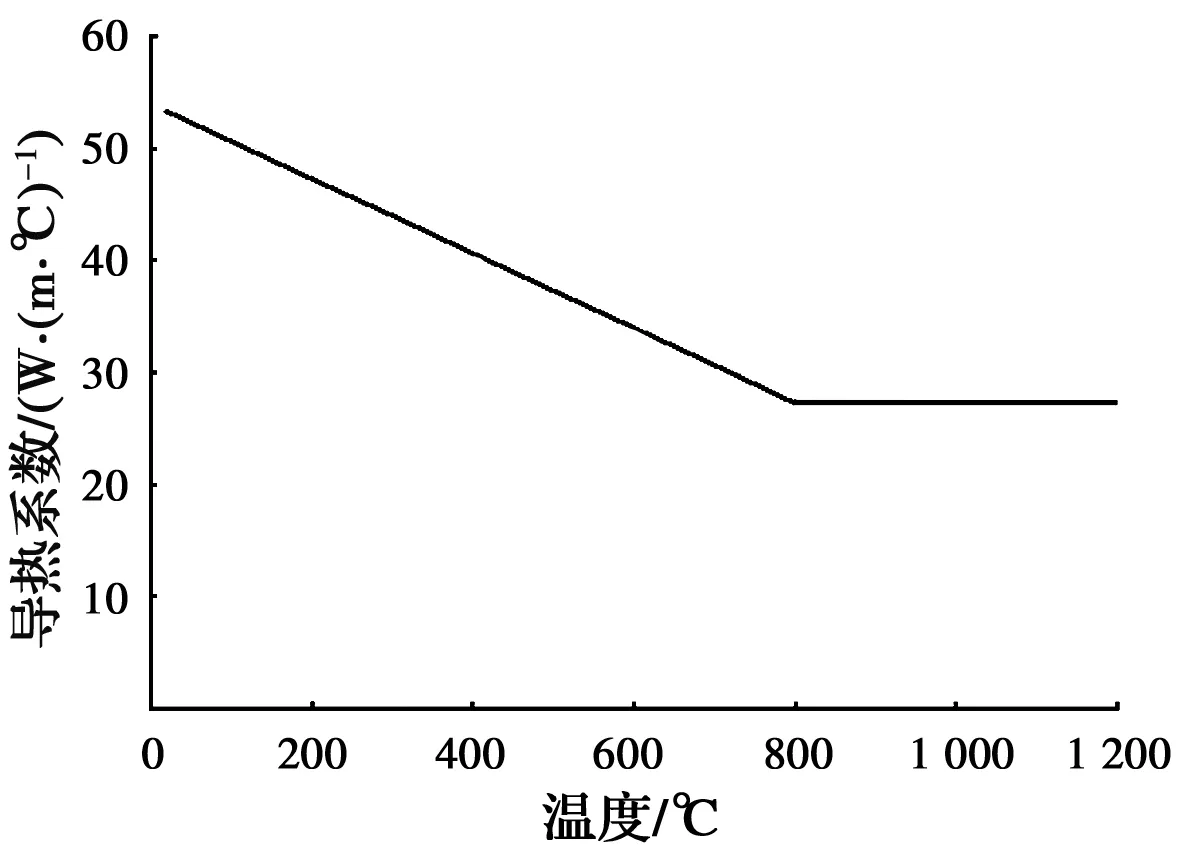
图9 钢材导热系数曲线[28]

图10 钢材比热容曲线[28]

1.3.4 胶合板在试件1楼板体系中，胶合板被用作背火侧结构板，仍需考虑其在火灾下的烧蚀行为。根据Jatheeshan等[26]的建议对高温下的胶合板导热系数进行取值，其导热系数逐渐增大，如图11所示。

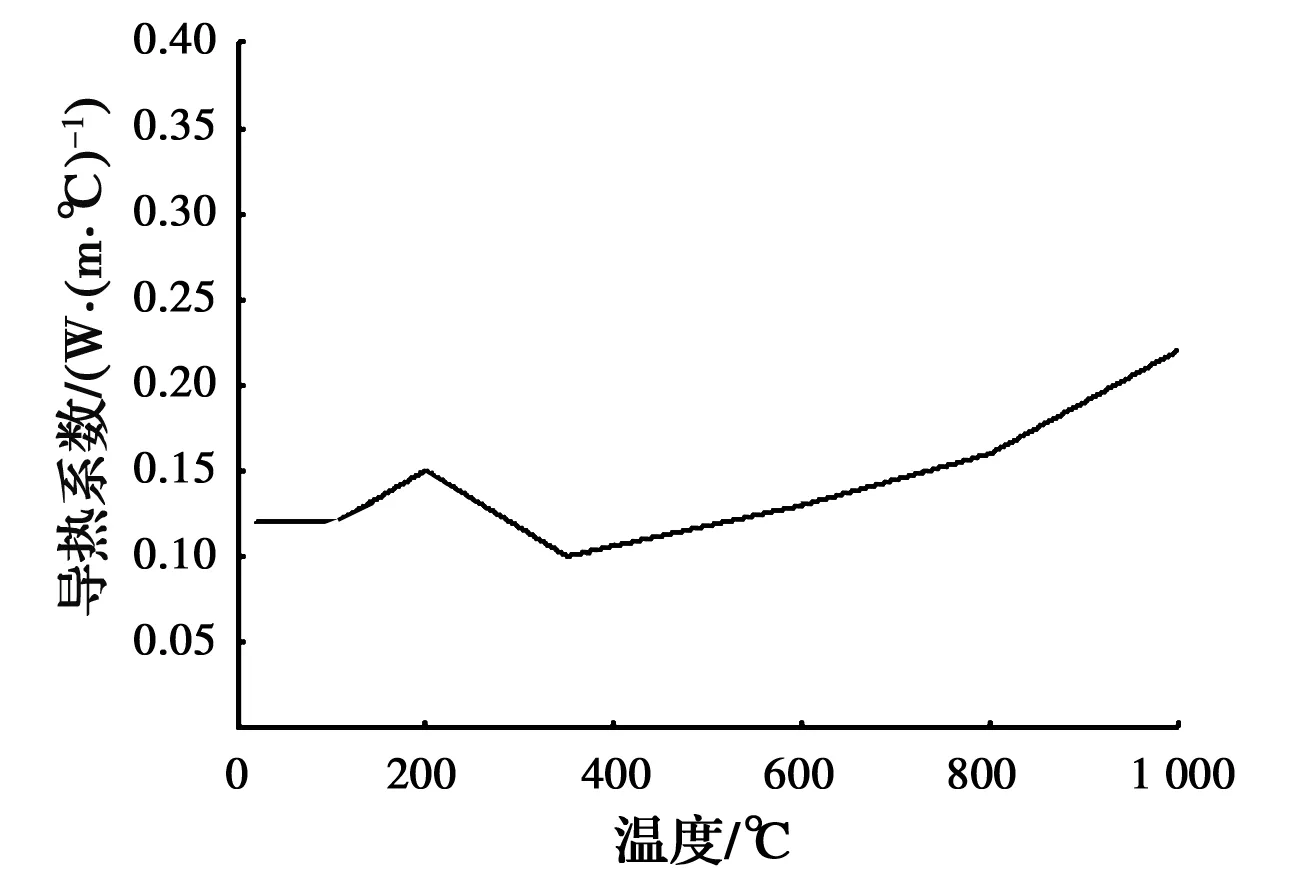
图11 胶合板导热系数曲线[26]

由于试件1胶合板未直接接触靠火侧石膏板，所以忽略100～105 ℃的比热峰值，取恒定值1 500 J/(kg·℃)[26]。胶合板的含水量约为9%～11%，在100 ℃时板材内部水分以水蒸气的形式释放出来。同时，其在高温下燃烧的现象，均会导致相对密度随着温度的升高而降低。胶合板环境温度下密度为500 kg/m3[26]，采用BS EN 1995-1-2[30]的建议进行高温下相对密度的取值，如图12所示。

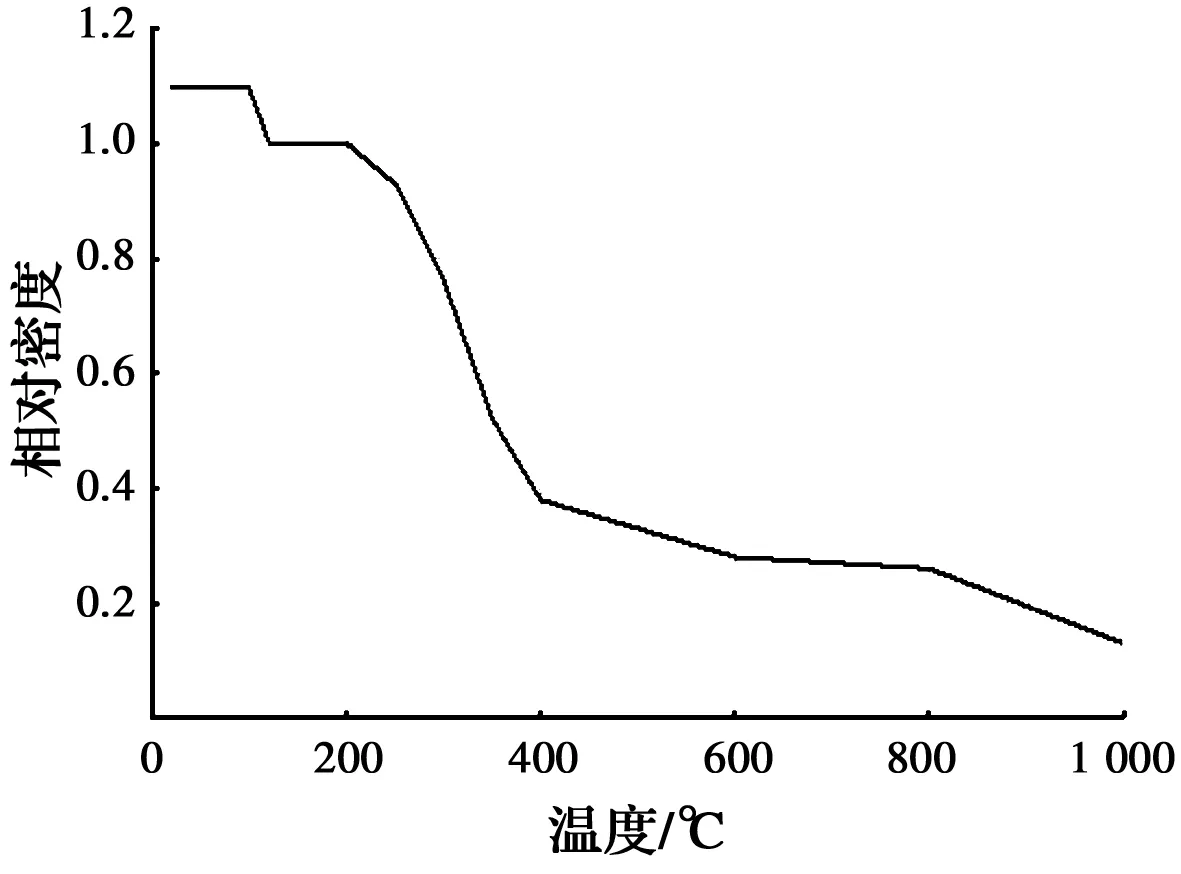
图12 胶合板相对密度曲线[30]

1.4 传热分析与验证

两个试件在数值模拟和试验中不同板材表面(受火面、背火面、板材间的面、受火侧空腔表面以及背火侧空腔表面)上的平均温度发展曲线，如图13、图14所示。

图13 试件1的试验与模拟结果对比

在图13中，数值模拟结果与试验结果吻合较好，仅P1-P2面的计算结果在65 min后略高于试验值，原因是采用的石膏板导热系数在1 000 ℃后快速增大，热量传递增加。试件2传热分析的计算结果与试验数据整体吻合较好，见图14。

图14 试件2的试验与模拟结果对比

两个试件在数值模拟和试验中两根中间托梁J2、J3(热翼缘、腹板、冷翼缘)的平均温度发展曲线见图15～图16。

在图15～图16中，托梁模拟计算的温度在60 min前均略低于试验值，原因是板材内部水分在高温下蒸发成水蒸气，导致空腔内存在水分子的迁移、相变过程，这会使托梁上的温度测点在前期所测温度值偏高。

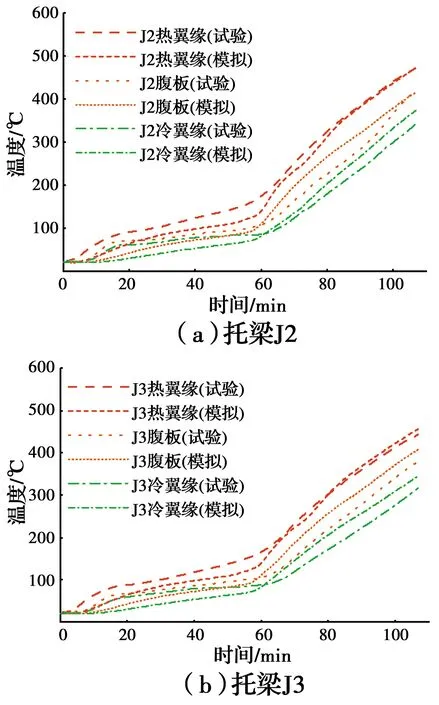
图15 试件1中托梁的试验与模拟结果对比

图16 试件2中托梁的试验与模拟结果对比

图15中，火灾发生60 min后，两根托梁热翼缘的升温与试验结果非常接近，托梁腹板、冷翼缘的计算值与试验值吻合较好，最大温度差值为31 ℃。

在图16中，钢托梁腹板与冷翼缘的计算升温曲线与试验数据吻合较好。托梁J2和J3热翼缘的计算结果略小于试验所得数据，可给出的解释是：模型未考虑托梁中自攻螺钉的热桥效应，略微减少了传递至热翼缘的热量；使用的材料热工参数与试验材料有一定的差异。

整个火灾过程中，试件1和试件2背火侧石膏板的最高温度均未超过160 ℃，试件未丧失隔热性。

1.5 与二维传热模型的对比分析

二维传热模型一般采用结构中部截面建立模型，仅能考虑单个截面的温度发展，不能考虑到结构沿跨度方向截面的变化及结构部分受火等因素造成的不均匀温度发展[22]，有使用局限性。

以试件1中0.25和0.5长度处截面建立二维传热模型，对比三维模型分析托梁J2热翼缘的温度发展情况，具体位置及编号见图17。二维传热模型中，相交部分定义绑定连接；材料热工参数和热边界条件同三维传热模型一致。

图17 传热模型对比点示意图

图18显示了以A和B点截面建立的二维传热模型在ISO-834火灾下107 min时的温度分布。与三维传热模型结果对比如图19(a)所示，可以发现，二维模型A点的升温远低于三维模型A点，是因为根据A点截面建立的二维传热模型默认结构沿跨度所有截面形状均一致，然而受火侧空腔面存在200 mm宽的背挡块石膏板(图17)，空腔截面形状已改变。由图19(b)可见，B点的升温存在一定差异，是因为三维模型中一部分热量被背挡块石膏板吸收，B点建立的二维模型不能考虑到背挡块的存在，因此，三维模型B点处的升温略小于二维模型B点。同时，图19中二维模型的A、B截面之间J2热翼缘的升温曲线差异较大。

图18 二维传热模型温度分布

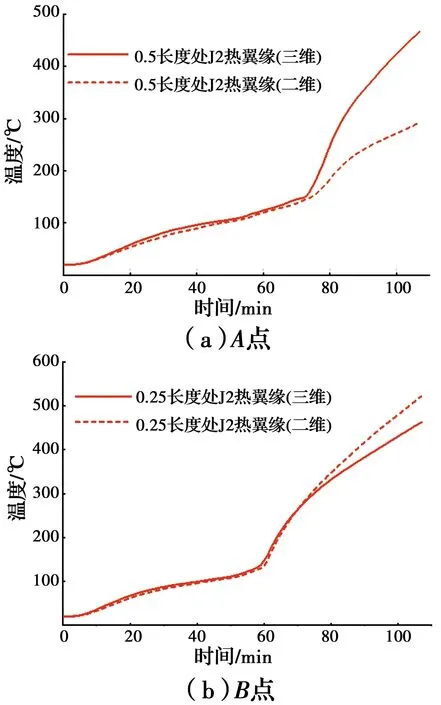
图19 二维与三维传热模型的升温对比

整体来看，三维传热模型的计算结果与试验数据整体吻合程度较好，且能考虑到结构构造等因素造成的不均匀温度发展。

2.1 模型的建立

图20 冷弯薄壁型钢楼板体系的边界条件及加载方式

2.2 材料力学性能

所用1.15 mm厚的G500冷弯薄壁型钢屈服强度和弹性模量分别为612、210 260 MPa，泊松比为0.3。根据文献[16]，采用弹塑性材料模型模拟火灾环境下冷弯薄壁型钢的非线性行为，并且钢材的弹性模量、屈服强度等力学性能随着温度的升高而下降。

表2给出了Kankanamge等[33]提出的冷弯型钢高温下力学性能折减系数，以精确模拟高温下冷弯薄壁型钢力学性能降低的影响。

表2 冷弯型钢的高温力学性能折减系数[33]

由于火灾条件下钢托梁的温度不均匀发展，钢托梁将受热膨胀，引起一定程度的热弯现象。欧洲规范BS EN 1993-1-2[28]给出了钢材热伸长率的建议公式。

2.416×10-4

20 ℃≤Ts≤750 ℃

(1)

对式(1)求导，得到钢材的热膨胀系数

αs=0.8×10-8Ts+1.2×10-5

20 ℃≤Ts≤750 ℃

(2)

式中：L为长度，mm；αs为热膨胀系数，1/℃；Ts为温度，℃。

背火侧胶合板与石膏板的力学性能见表3。胶合板根据BS EN 1995-1-2[30]对高温下木材的力学性能进行调整；石膏板由于其常温强度较小，未予以高温下力学性能的调整。

表3 胶合板和石膏板力学性能

为确定建立的楼板模型与试验试件力学性能符合，计算整个楼板体系在20 ℃下的极限承载能力为94 kN，与Baleshan等[8]试验的90 kN极限荷载工况较为相近，可做参考。

2.3 初始几何缺陷和残余应力

残余应力影响托梁抗弯强度，导致其抗弯强度降低。随着温度的升高，托梁内部残余应力迅速减小。根据Baleshan等[18]的研究结论以及既有研究常用方法，火灾条件下可以不考虑残余应力。

2.4 耐火失效准则

1)稳定性。对于抗弯构件，试件超过以下任一判定准则时，均认为试件丧失承载能力。

极限弯曲变形量

(3)

极限弯曲变形速率

(4)

式中：D为极限弯曲变形量，mm;L为试件的净跨度，mm；d为试件截面上抗压点与抗拉点之间的距离，mm；试件1、试件2的d分别为231 mm和269 mm。

2)隔热性。试件背火面温度温升发生超过以下任一限定情况均认为试件丧失隔热性：平均温度温升超过初始平均温度140 ℃；任一点的温度温升超过初始温度180 ℃。

3 三维热力耦合分析的验证

火灾条件下，钢托梁强度下降，且非均匀升温膨胀，试件挠度逐渐增大。整个试验过程中，试件背火侧温度均低于耐火失效温度160 ℃(图13、图14)，满足隔热性要求。火灾升温环境下，托梁挠度迅速增大，从而丧失稳定性。

3.1 试件1的模拟分析

3.1.1 托梁的挠度发展图21(a)为环境温度下加荷步骤后的托梁J2，其最大垂直挠度为4.56 mm。图21(b)显示了火灾下升温114 min时，由于钢材受热膨胀和高温强度降低的影响，托梁J2的跨中挠度显著增大，达到32.48 mm。

图21 托梁J2的垂直位移云图

火灾环境下，托梁J2跨中挠度在110 min时有显著增大，构件逐渐丧失稳定性，如图22所示。最终得到的耐火失效时间为114 min，文献[18]数值模拟预测的失效时间为120 min。从挠度分析结果看，相比文献[18]，模型的精度改善作用明显，原因为：使用的温度场为三维传热模型计算的非线性结果，而文献[18]施加的温度场为沿跨度方向均相同的简化线性温度分布；对背火侧板材、轻钢构件之间的连接方式和接触传力关系定义更为精细。

图22 试件1托梁J2的时间挠度曲线

数值模拟的托梁冷翼缘处的胶合板约束始终存在，直到结构耐火失效。而事实上，胶合板部分烧焦以及冷翼缘自攻螺钉屈曲等将对托梁挠度的发展造成影响。因此，数值模拟的耐火时间比试验结果略长。

3.1.2 托梁的应力发展起初托梁受力产生应力，随着火灾下托梁内部温度升高，强度下降，最后达到与温度相关的屈服应力，托梁耐火失效时的von Mises应力分布如图23所示。在图23中，托梁J2支座和加荷处的冷翼缘出现最大von Mises应力。图24显示了这两处von Mises应力与屈服应力随时间变化的曲线。

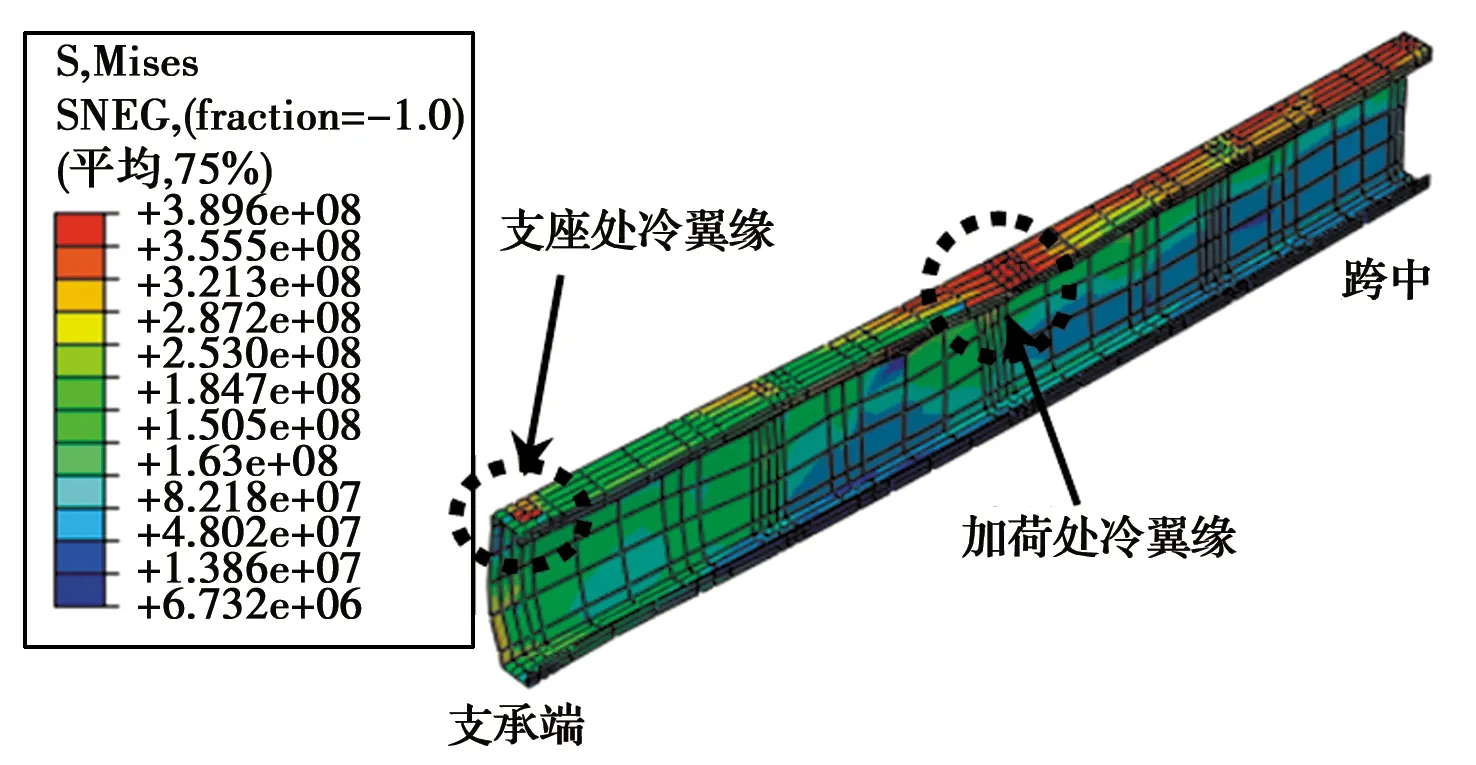
图23 试件1托梁J2的von Mises应力分布

从图24可看出，支座处冷翼缘与加荷处冷翼缘达到屈服强度的时间有所差异，在114 min时托梁丧失稳定性。图24中的虚线有所差异，是因为使用的温度场为非线性温度分布，这两处同为托梁冷翼缘，但温度发展并不完全一致，导致与温度有关的屈服应力值略有差异。

图24 托梁J2屈服处应力发展曲线

3.1.3 失效模式数值模拟结果显示，托梁未发生绕弱轴的弯扭屈曲，与试验结果[8]一致。试验和数值模拟中，托梁腹板沿长度方向均呈现波浪状屈曲的失效模式，如图25(a)所示。托梁J2在支座处均发生局部屈曲破坏，如图25(c)所示。图25证明了经数值模拟的失效模式与试验结果一致。

3.2 试件2的模拟分析

图26为火灾下数值模拟157 min耐火失效时，试件2托梁J2的垂直挠度达到最大值35.69 mm，此时支座处和跨中冷翼缘达到屈服应力，结构丧失稳定性。失效模式与试件1相同(图25)，均为支座处局部屈曲和沿跨长的腹板屈曲。图27为数值模拟、火灾试验及Baleshan等[18]的托梁挠度随时间的变化曲线。