基于BP算法的片上学习CNN硬件加速器
2021-09-06张多利王泽中宋宇鲲
王 飞, 张多利, 汪 杨, 王泽中, 宋宇鲲
(合肥工业大学 电子科学与应用物理学院,安徽 合肥 230601)
近年来,随着深度学习广泛应用,嵌入式系统中专用的低功耗深度学习处理器受到关注。深度学习包含训练和推理2个运算阶段。由于训练运算过程非常复杂,使得硬件设计难度激增,功耗和价格随之上涨,大多数深度学习硬件将注意力集中在推理阶段[1]。
当深度学习芯片不具备片上训练能力时,需要将数据上传至服务器端训练后更新本地模型,这样会带来2个问题:① 深度学习模型的参数量一般非常大,更新需要高带宽、稳定的网络连接;② 隐私数据包括指纹、视网膜等,在网络中传输会带来安全问题。因此,有片上学习功能的深度学习硬件近年来成为研究热点,目前已有一些研究成果。
文献[2]提出的Socrates-D架构是一种可以实现片上学习的多核并行深度学习硬件,计算单元内使用2T1C的eDRAM,可以在不改变地址规则的情况下进行全连接层的训练;文献[3]提出的Eyeriss架构通过将二维卷积运算按行分解为一维卷积与部分和累加运算,并固定部分数据在片上存储器中,可以有效降低芯片功耗,同时实现高效的片上推理与训练过程。
作为深度学习的代表性应用,卷积神经网络(convolutianal neural network,CNN)在数据分类和目标识别领域表现优异。为了实现CNN的推理与训练,本文提出一种带有内部离散式存储结构的计算单元,在不改变地址规则的情况下进行矩阵转置乘运算,采用运算过程分割的运算阵列,以达成兼顾推理和训练功能的硬件结构。
1 CNN算法
1.1 推理与训练过程
典型的CNN由多个计算层组成,依次包括若干个卷积层、池化层以及全连接层。卷积层的推理过程为:
(1)
其中:l为网络层数(l=1,2,…,L);K为卷积核;X为特征图;B为每层对应的偏置;σ为激活函数。卷积层后是池化层,将特征图分割为若干个区域后取均值或最大值输出。
全连接层的推理过程可以用矩阵运算表示,即
Xl=σ(WlXl-1+Bl)
(2)
其中:X为输入和输出向量;W为权值矩阵。
CNN的训练过程通常基于梯度下降法,通过误差反向传播(backpropagation,BP)算法更新参数[4]。在训练过程中,输出层n维向量XL都有对应的理想输出向量T,误差E可定义为:
(3)
而BP算法的目的是通过更新各层的参数,使得E对整个数据集取最优解[5],涉及的推理和训练运算见表1所列。

表1 CNN推理与训练涉及的运算
1.2 卷积运算
本系统中的卷积运算分为2类:① 推理和误差反传中的小卷积核运算;② 权值更新时大尺寸卷积核运算。针对这2种类型,有2种运算方式。
1.2.1 卷积分解运算
为提高小尺寸卷积核的卷积计算效率,本系统采用卷积分解和离散式缓存结构,提高数据复用率和运算效率。二维卷积运算分解后如图1所示,分解后的卷积运算可以使用1组一维算术逻辑单元(arithmetic and logic unit,ALU)阵列实现。
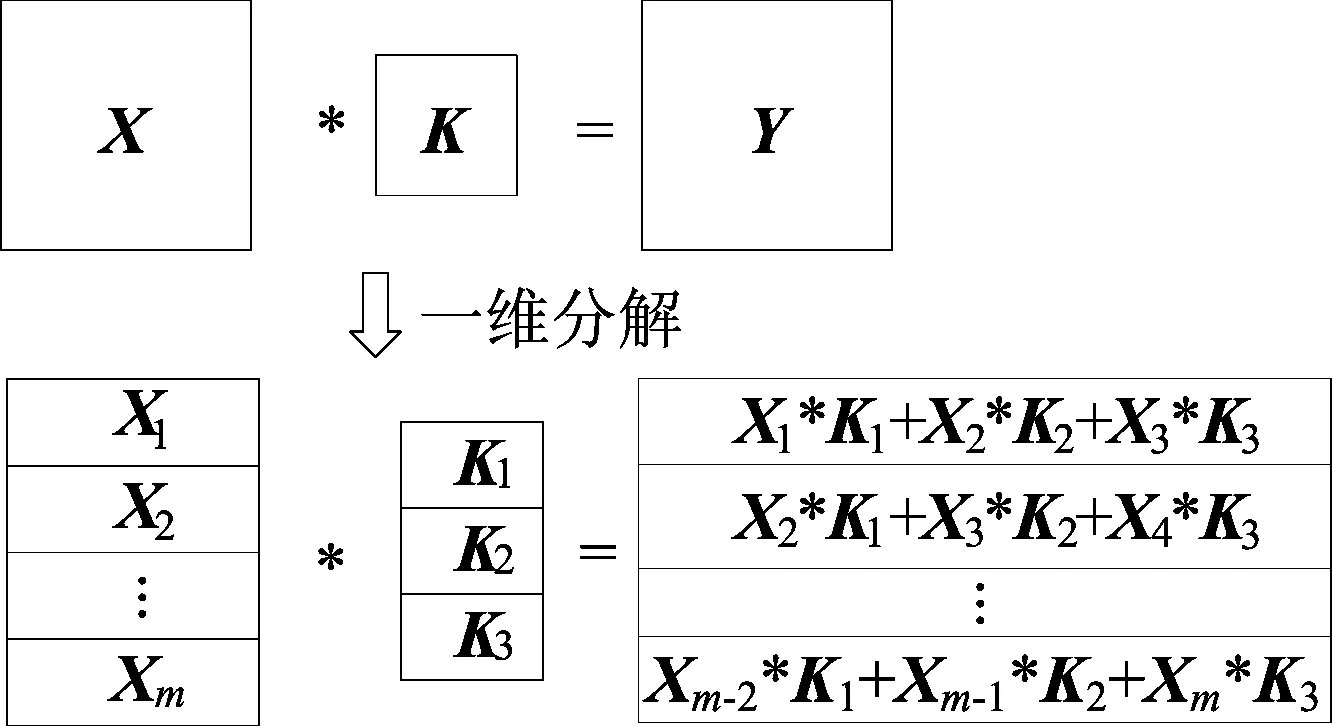
图1 二维卷积分解为一维卷积
在CNN中,卷积运算通常是多输入多输出通道的。对于多输入通道,可以按顺序排列输入特征图和对应的卷积核,通过输出的缓存数据累加实现,不增加新的硬件资源。对于多输出通道的卷积运算,可以通过并行上述的一维ALU阵列构成二维运算阵列实现。
1.2.2 矩阵乘形式卷积
针对大尺寸卷积核,可以将卷积展开为矩阵乘法进行运算,按此方法展开的输入特征图为分块的类似Toeplitz矩阵形式,如图2所示[6]。输入特征图的分块在横向上与卷积核尺寸相同,在纵向上与输出特征图的尺寸相同。

图2 卷积运算展开为矩阵乘法
Toeplitz矩阵的特点在于主对角线元素相等,平行于主对角线的线上元素也相等,矩阵中各元素关于副对角线对称。
2 CNN加速器的结构设计
2.1 CNN加速器架构与计算阵列配置形式
为了适应CNN运算中涉及矩阵卷积、向量运算等多类型运算,本文提出了基于指令配置计算资源的CNN加速器设计方法,将CNN运算过程分解为128位低层次的运算指令[7],如图3所示。

图3 CNN加速器指令格式
根据运算类型不同,输入和输出数据有各种不同的组织形式,需要进行数据分配与结果缓存。本系统框图如图4所示。

图4 CNN加速器系统框图
本系统的计算阵列包括1组二维排列的处理单元(processing element,PE),每个PE包含1个乘法器、1个加法器及若干寄存器组。计算阵列根据PE可划分为二维阵列,而根据处理过程可划分为乘法和加法2层,如图5所示。
通常PE中乘法器和加法器直接相连,形成一个乘累加器,这样的乘累加器可以处理矩阵乘、卷积等运算。2×2计算阵列处理矩阵乘向量的配置形式(模式A)如图5a所示。
训练过程中涉及的矩阵转置后乘向量的运算,需要将单个PE中的乘法器和加法器分离,每个PE单独处理乘法,然后相邻PE的乘法结果传递至一个加法器相加,形成加法树结构(模式B),如图5b所示。

图5 计算阵列的2种配置模式
2.2 计算单元设计
计算单元设计结构如图6所示。图6中,reg表示寄存器(register)。

图6 计算单元设计结构
寄存器组包含矩阵组、向量组、中间结果缓存3类。矩阵组按行缓存数据重用率低的数据,包括全连接层的系数矩阵和卷积层的特征图。向量组缓存需要重复使用的数据,包括缓存全连接层的激励向量和展开为向量形式的卷积核。中间结果缓存只在卷积计算时使用,此时x信号置0。用于中断卷积中的部分和累加。
为实现计算阵列的2种配置模式,加法器的输入需要通过多路选择器(multiplexer,MUX)进行选择。本文中每个加法器的每个输入口最多有2种选择,这样的设计避免了MUX的输入选择过多导致系统性能下降。
2.3 数据分配器
在计算过程中,数据分配器负责将要进行计算的数据分配至对应的PE中,包括向量分配、全连接层分配、卷积层分配及权值更新分配。
全连接层计算过程中,分配器首先读入激励向量,然后在计算过程中补充各PE的矩阵组数据。本系统在读取时先将矩阵分块,然后按行读取数据。分块的原则如下:① 根据运算节拍在行方向分块,确保每个PE中都有数据进行运算,避免资源空闲;② 根据PE数量在列方向分块。
在卷积层进行计算时,按一定顺序读入卷积核和输入特征图,进行相应的地址跳变。这2种矩阵的尺寸参数均在指令中有体现,根据这些参数就可以进行地址运算。以输入特征图为例,读入顺序为:各图第1行→各图第2行→…→各图最后一行。
2.4 权值更新流程
2.4.1 全连接层
全连接层的权值更新公式为:
W3←W3+ηs3·(X3)T
(4)
此运算需要2条指令,分解后如下:
s3←ηs3
(5)
W3←W3+s3·(X3)T
(6)
(5)式运算时,图3指令中[31:0]段变为学习率,直接复制写入矩阵组即可,运算完成后写回至s3原地址。(6)式运算时,将s3写入矩阵组,X3写入向量组,W3通过图6中x通道写入,完成运算后直接写回。
2.4.2 卷积层
卷积层的权值更新公式为:
ΔK1=s1*X1
(7)
K1←K1+ηΔK1
(8)
按1.2.2节所述的矩阵乘形式卷积可以用于计算(7)式。通常的矩阵与向量乘法只能用若干一维PE进行,而由于Toeplitz矩阵的性质,副对角线元素和与其平行的线上元素可以直接复制,因此可以从第2行开始在矩阵前添加适当的空信号,写入的1个数据可以在多个PE中使用。以输入特征图X尺寸为50×5、卷积核K尺寸为48×48为例,需要调用3×3的PE,输入特征图的数据流如图7所示。

图7 Toeplitz矩阵形式的输入特征图
对于输入特征图X,首先按行分解为X1,X2,…,X50,同时写入所有PE。对于PE第2行,X1无需进行计算,第3行PE的X1和X2同理,此时该行处于不激活状态。对于分解后的每行数据Xm,每个元素同样有不激活状态,如图7中灰色部分。
其中卷积核数据使用图6的y和z路径在PE间流动。其中PE 2.1和3.1中,向量组寄存器的写地址比读地址小50,形成K的多周期延迟效果。其余PE中写地址与读地址相同,形成单周期延迟效果。
2.5 激活函数模块
本系统中使用的激活函数包括ReLU和Sigmoid 2种,要同时求其导数。ReLU函数的实现不再赘述,Sigmoid函数及其导数如下:
s(x)=1/(1+e-x)
(9)
s′(x)=s(x)[1-s(x)]
(10)
本文采用分段非线性拟合法实现Sigmoid函数[8],公式为:
p(x)=ax5+bx4+cx3+dx2+ex+f=
[(ax+b)x2+cx+d]x2+ex+f
(11)
同时,根据函数的对称性,有
s(x)=1-s(-x)
(12)
因此,只需要拟合[0,+∞)区间即可。由于还需要计算导数,(12)式运算不可避免。激活函数计算模块如图8所示,最大绝对误差为9.885 7×10-7,可以满足高精度拟合要求。

图8 激活函数模块
3 CNN加速器性能评估
3.1 资源消耗
为了方便与PC端对比计算准确性与加速比,本文在系统实现时采用32位单精度浮点数,在Xilinx XC6VLX760-FF1760现场可编程门阵列(field-programmable gate array,FPGA)上实现,资源消耗见表2所列,当浮点运算IP核的流水延迟设置为4时,最高工作频率为187.083 MHz。

表2 资源消耗统计结果
3.2 实验性能评估
本系统采用PC+FPGA的架构对加速器进行测试,包括计算准确率和运行时间,并与CPU、GPU进行对比。其中CPU型号为IntelCorei5-9400F,主频2.9 GHz;GPU型号为NVIDAGTX1080Ti,显存容量11 GiB;FPGA运行频率设为100 MHz。测试方案如图9所示,使用以太网口在PC和FPGA间进行数据交互。
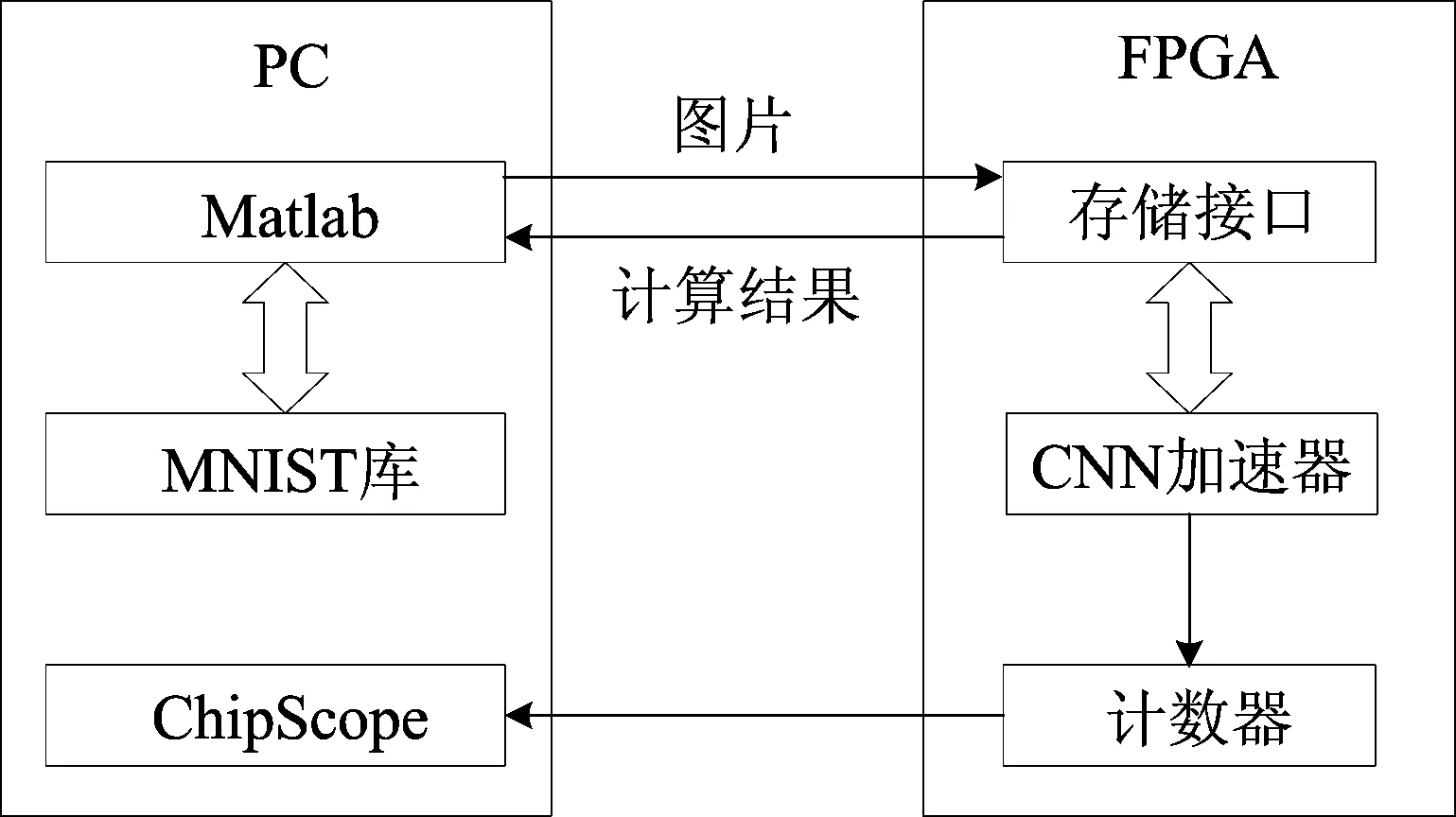
图9 测试方案与模型
验证采用的模型如图10所示,推理过程包含58 084次乘累加运算,训练过程包含123 616次乘累加运算,需要训练21 450个参数。图10中,Conv-1、Conv-2为卷积层,Pooling为池化层。

图10 验证CNN模型
单次推理和训练过程误差见表3所列,单次累计误差为8.043 7×10-6。
注:FC-1、FC-2为全连接层(fully connected layer)。
由表3可知:在推理过程中,卷积层会增大误差,而全连接层会减小误差,这是由于卷积层中的权值共享导致绝对误差的积累,而全连接层的权值误差可中和;权值更新过程中,卷积层的更新会导致明显的误差,这也是由于大尺寸卷积核的权值共享导致的。
在大量数据训练时,每次训练的误差积累会导致PC与FPGA的CNN模型完全不同。大量训练次数下的识别率见表4所列。
由表4可知,在FPGA上的识别率比在PC上低0.63%。
本文使用的CNN在CPU、GPU及FPGA平台上的运行时间见表5所列。由表5可知,本系统在FPGA上运行相比于CPU达到了7.67倍加速效果。但由于本系统使用数字信号处理器(digital signal processor,DSP)对单精度浮点数进行乘累加运算时,乘法结果需要等待上一帧加法结果才能进行下一步运算,无法发挥流水线的优势,因此运行速度略逊于GPU实现。
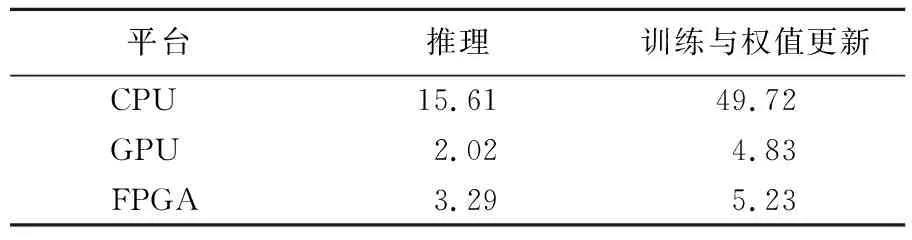
表5 3种平台计算时间对比 单位:ms
4 结 论
本文考虑了便携式应用场合对片上学习CNN硬件加速器的需要,研究了基于BP算法训练CNN模型的原理与运算特点,设计一种可实现片上学习的CNN加速器,通过可配置数据流的二维运算阵列与数据分配器,提高了CNN各层运算的并行度;在Xilinx Virtex6 FPGA芯片上,实现了IEEE-754标准[9]下32位单精度浮点数CNN模型的训练过程,在保证识别率的前提下运行速度明显优于PC端。
