“田忌赛马”中的社会契约与创新激励

陆文玥 刘志阔 段剑辉

摘要：“田忌赛马”反映了在保持社会契约的权威性和激励人力资本创新方面的策略观。基于现代契约经济学理论，从“立约-违约”双向契约叙事视角出发，文章通过构建博弈模型，提出序贯博弈下齐王的“相马”策略，探究其中蕴含的人力资本产权和创新激励机制。在对剩余控制权和剩余索取权的争夺中，马匹的能力和序贯博弈为齐王提供了控制权优势，同时通过交换收益权，激发“创造性破坏”，在维护社会契约权威性的同时激励创新。

关键词：田忌赛马;契约经济学;人力资本;创新激励

一、文献综述

对“田忌赛马”问题，国内学者分别从策略性、是否存在违规、选拔机制、赛马历史等方面进行了研究。陕声祥（2017）认为，出马顺序是赛前共同约定的重要规则，田忌通过改变这一规则而获胜，反映出他重功利、轻规则，因此胜之不武。柯政（2016）认为，“赛马”助长了考生从功利而非兴趣或特长出发选择科目的倾向，因此这种激励机制不利于选贤用能。张建发（2017）认为，田忌并未突破规则，而是通过灵活变通的方式提高了比赛的绩效。尹向飞和陈柳钦（2006）建立了模型，验证了田忌的出马顺序是最优策略，提出存在权能谋事的最优策略定理。崔立根（2014）认为，赛马实为一种政治活动，旨在通过竞争与沟通选拔人才，而非选拔良马。

本文将齐王与诸公子（整体）之间的赛制约定视为一种权威性的社会契约（一级契约），将齐王-田忌-其他诸公子的非合作博弈视为一种竞争性契约（二级契约）。由于契约是不完全的，赛马者之间必然存在着对剩余控制权和剩余索取权的争夺。就机制设计而言，是否存在着一种既保证参与约束又提供激励相容的机制？换言之，齐王在确保社会契约条件下的控制权基础上，如何通过收益权的转让激励孙膑这样的人才脱颖而出？

假设1：一级契约具有权威性。

假设2：一级契约下的承诺未必可信。

假设3：违约须具有程序正义性。

假设4：二级契约下存在信息不对称。

假设5：二级契约下存在集体行动逻辑。

假设6：各小国间存在竞争性的人才市场。

二、一級契约与序贯博弈

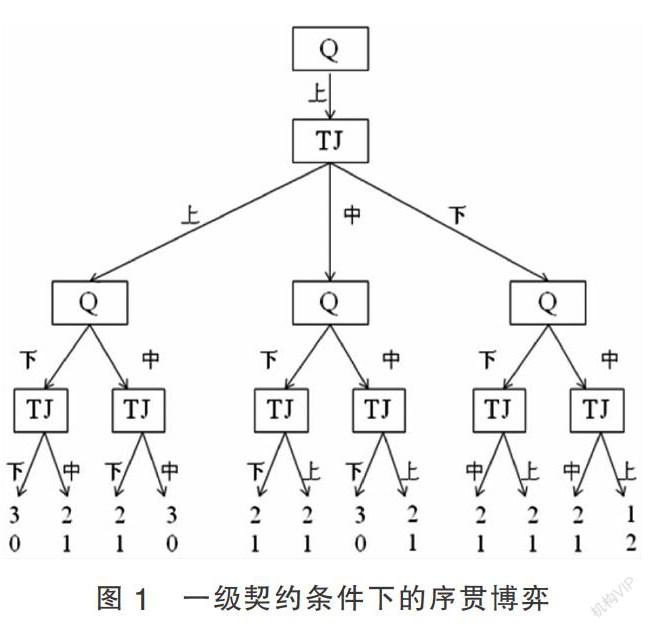
假设将“诸公子”视为一个整体，该比赛是“诸公子”T和齐王Q之间的一场2×2零和博弈。但在操作层面，赛马是按“下-上”、“上-中”、“中-下”的回合分三轮进行的，因此实际上是一种序贯博弈。齐王在第二轮具有权变的权利，即根据田忌在第一轮的策略适时调整战术的权利。如图1所示，齐王和田忌分别用Q和TJ表示，每轮马匹的品级由上、中、下表示，按照三局两胜的惯例，在第二轮结束时即可确定二人的得分，设每轮胜出得1分，每轮失败得0分，支付如下。

由图1可知，由于齐王拥有事后权变机会，因此田忌以“下-上-中”获胜的概率只有，全盘皆输的概率为，获胜一轮的概率为，而齐王获胜的概率则达。可见，齐王在比赛中具有绝对的控制权优势，因此一级契约的存续是有保障的。无论是从齐王马匹的能力还是从序贯博弈所带来的主动权而言，齐王都没有必要主动违约。此外，齐王的承诺之所以可信，还与诸公子内部的集体博弈困境有关，即二级契约博弈。

三、二级契约与集体行动博弈

假设存在两种契约类型，既定契约a和备选契约集B，二者同时竞争，bi∈B，nb≥2。在不完全契约条件下，a有被违约的可能，即a有被bi替代的可能。假设替代策略为S1或s1，不替代策略为S2或s2。如果bi优于a，则有替代的可能，概率为0≤pi≤1，p1+p2+…+pi=1，i∈n为。然而，由于存在违约和再谈判等导致的交易费用，因此可视为既有契约a对任何替代者的潜在惩罚，设为支付-α（α>0），而如果维持a，则不存在这一支付，即α=0。于是，bi面临两种效用因素，即替代a和遭受a的惩罚。在一场“赢者全得”的博弈中，胜出者得到支付w（w>0），其他得到支付0。同时，bi会预期到，即使替代了a，也将面临契约集B中其他契约替代的潜在可能性。假设在a契约仍为所有当事人所遵守的情况下，B中各契约均为备选契约，彼此之间存在竞争但不存在惩罚，惩罚只来自既有契约a对bi潜在替代的反应。换言之，即使bi成功替代a（同时获得支付-α），也并不能确保自身不受B集合中其他成员发起替代，故其预期支付为EVi=-α×（1-pi）+（w-α）×pi=wpi-α。现仅考虑B集合中任意两个契约b1和b2之间的博弈（见图2）。

经推导可知①，b1和b2分别选择发起或不发起替代行为作为其占优策略的条件如表1所示。

此外，当w>α且wpi<α时，存在两个纳什均衡，即（s2，S1）和（s1，S2），b1和b2均无占优策略。这是一个“贡献博弈”，即尽管各方都希望对方承担贡献公共品的成本，但并不能排除自己做此贡献并独自承担成本（或交易费用）的可能。然而，本例中，不仅面对公共品成本问题，还面对收益激励问题，因此需要进一步分析。由于二者在此条件下均无占优策略，因此考虑契约数量的影响。

假设这些竞争性契约个体在体现整体特征方面是均质的，因此将它们各自发起替代的行为视为具有相同的概率值γ。如此，假设bi发起替代行为的概率为γ，不发起的概率为1-γ。除bi以外，其他所有n-1个参与者都发起替代行为的概率为γn-1，而不发起的概率为1-γn-1。以P1为例。在均衡条件下，它对两种选择是无差异的，因此设其纯策略的预期支付相等，即

EV1=γn-1×（wp1-α）+（1-γn-1）（w-α）=0

s.t. w>α，wp1<α

经计算得

γ=[]

对wp1<α两边乘以-1，再加上w，得w-α