基于组合预测模型的低值医用耗材库存需求预测

张林灵，郑焜

浙江大学医学院附属儿童医院 医疗设备科，浙江 杭州 310006

引言

医用耗材是指经药品监督管理部门批准的使用次数有限（包括一次性及可重复使用）的消耗性医疗器械[1]。按照价格，医用耗材可分为高值医用耗材和低值医用耗材。目前医院对高值医用耗材库存普遍采用“零库存”管理办法，对于使用频率高、需求量大的低值医用耗材库存则采用提前储备的管理办法。但是低值医用耗材的月消耗量不确定性大，库存管理存在难度[2]。月库存量大于月消耗量，将造成医院资源配置不合理；月库存量小于月消耗量，将影响患者的正常就诊。

调研发现，医院储备低值医用耗材库存的需求普遍通过临床科室意见汇集法获得[3-5]，每月各临床科室依照以往经验上报下月低值医用耗材需求，经设备科审批后，由采购中心负责采购。期间涉及多个部门的协调与交互，一旦在上报需求中发现问题，需要设备科递回相关科室，科室修改后重新提交。耗材需求上报过程周期长、环节多，消耗较多的人力和时间。为了提高低值耗材采购效率，本文探讨研究一种适合用于预测低值医用耗材库存需求的预测模型替代科室意见汇集法。

考虑到低值医用低值耗材的数据为按月统计，具有历史样本量小、无特定分布规律且随时间变化相对稳定的特点，兼顾到模型的预测效率与计算效率，本文提出一种基于二次指数平滑和灰色马尔科夫的组合预测方法来研究适用于低值医用耗材需求预测的预测模型，以期可以有效简化采购流程，提高医院的采购效率。目前，组合预测模型已经应用到零售、港口物流、电力输送等领域，并验证了其有效性[6-11]。Shaub[12]的研究证明组合预测具有普遍适用性和准确性。

1 方法

本文选用二次指数平滑预测模型和灰色马尔科夫预测模型进行组合建模。其中，二次指数平滑模型适用预测随时序变化相对稳定且未出现较大曲率的序列，灰色马尔科夫模型适用历史样本量小且不具有规律性分布的序列。本研究针对组合预测模型在低值医用耗材需求预测上的应用，主要研究组合模型中模型选取及权重确定问题，希望能够找到适合预测低值医用耗材需求的组合预测模型。由于预测模型需要利用历史数据进行建模，随着时间的变化，每月会产生新的数据加入到初始建模数据中，因此每隔一段时间需要对预测模型进行调整。为了方便研究，本文选定20 mL的一次性使用无菌注射器需求量为预测对象，以杭州某三甲儿童医院2017年1月至2018年12月的历史数据为基础（表1），预测2019年1—4月的变化趋势。

1.1 二次指数平滑预测模型

二次指数平滑模型是一种时间序列预测模型，运用回归分析法建立系列回归预测类模型。预测模型为yt+m=at+btm，其中m为超前，at和bt为待定系数。

分别对α取值0.1、0.15、0.2、0.25、…、0.9、0.95，比较α取不同值时的预测值和实际领用量的平均绝对误差。计算可得，当α=0.55 时均方误差值最小，即预测模型效果最好。

建立二次指数平滑预测模型为ym=10652.50-92.43m。

1.2 灰色马尔科夫预测模型

从而由累减得到预测值如公式(3)所示。

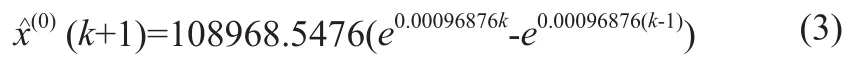
马尔科夫过程对于具有无后效性数据序列问题有着较高的预测精度，系统在t+1时刻的状态仅仅与t时刻所处的状态有关[14]。马尔科夫链是马尔科夫过程的一种。注射器领用量可以看成理想离散时间序列，适用于马尔科夫链，本文采用马尔科夫链对灰色预测模型预测值进行修正。

按照实际值和灰色模型预测值的残差比重，本文将残差比重在-10%～-5%范围内的称为状态1，残差比重在-5%～0%范围内的称为状态2，残差比重在0%～5%范围内的称为状态3，残差比重在5%～10%范围内的称为状态4。2017年1月至2018年12月的24个月份中，统计各状态出现频率如表2所示。

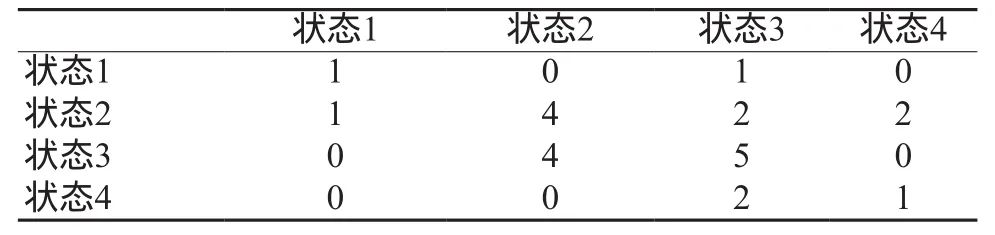
表2 状态转移频数统计表

依据状态转移频次，首先得到2019年1月的预测状态转移矩阵P(1)。

由于2018年12月处于状态2，参照矩阵P第二行的最大值0.45 ，考虑2019年1月最大可能处于的状态是状态2。状态2所处的残差比重范围是-5%～0%，所以取残差比重的中值对灰色预测值进行修正。

同理，2019年1—4月的状态转移矩阵如下。

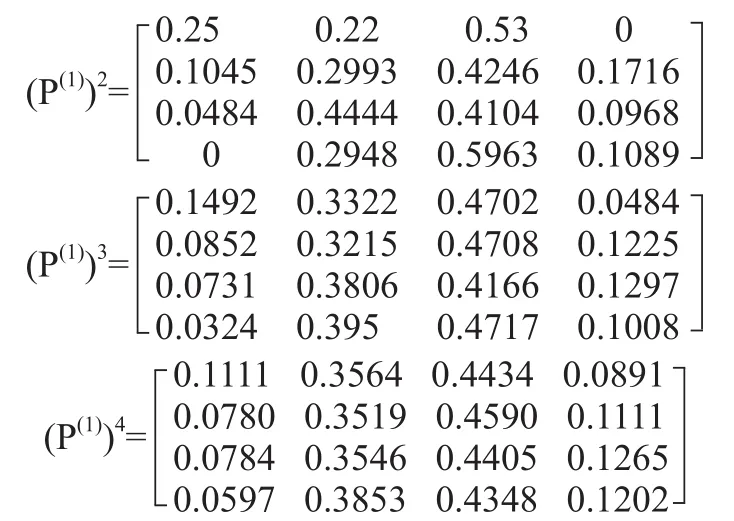
在灰色预测模型的基础上，经过马尔科夫误差状态转移矩阵修正最终可得预测数据。

1.3 组合预测模型

1.3.1 变异系数法

经计算可得组合预测模型为：y=0.55y1+0.45y2，其中y为组合预测值，y1为二次指数平滑模型预测值，y2为灰色马尔科夫模型预测值。根据组合预测模型的公式及各单一预测模型的预测值，可以计算出基于变异系数法的组合预测模型的预测值。

1.3.2 简单加权法

1.3.3 方差倒数法

2 结果

根据20 mL一次性使用无菌注射器2017年1月至2018年12月的历史领用数据，分别利用二次指数平滑预测模型和灰色马尔科夫预测模型对2019年1—4月的库存需求进行预测，预测结果如表3所示。

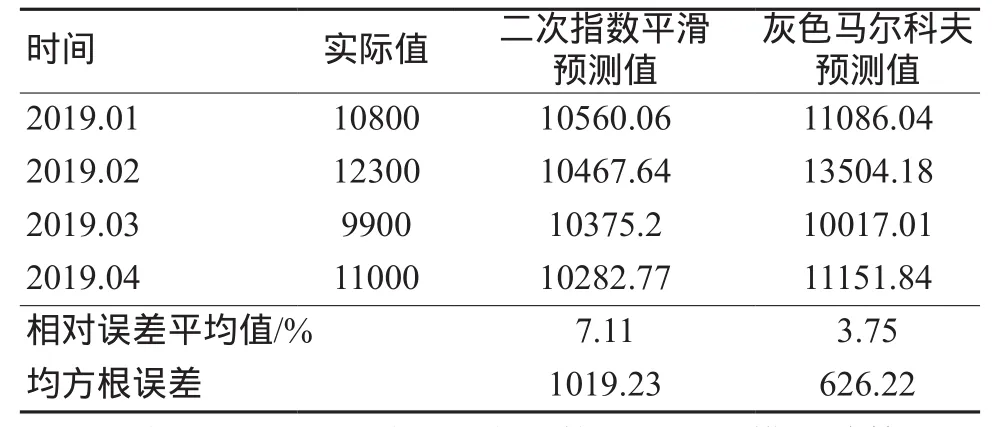
表3 2019年1—4月一次性使用无菌注射器预测结果（支）

从表3可以看出利用二次指数平滑预测模型计算得出的预测值与实际值偏差较大，相对误差平均值高于5%。相较于二次平滑预测模型，灰色马尔科夫预测模型的准确度较好，相对误差平均值小于5%。

三种分别由变异系数法、简单加权法和方差倒数法确定单一模型权重的组合模型的预测结果表4所示。A代表由变异系数法确定单一模型权重的组合模型，B代表由简单加权法确定单一模型权重的组合模型，C代表由方差倒数法确定单一模型权重的组合模型。

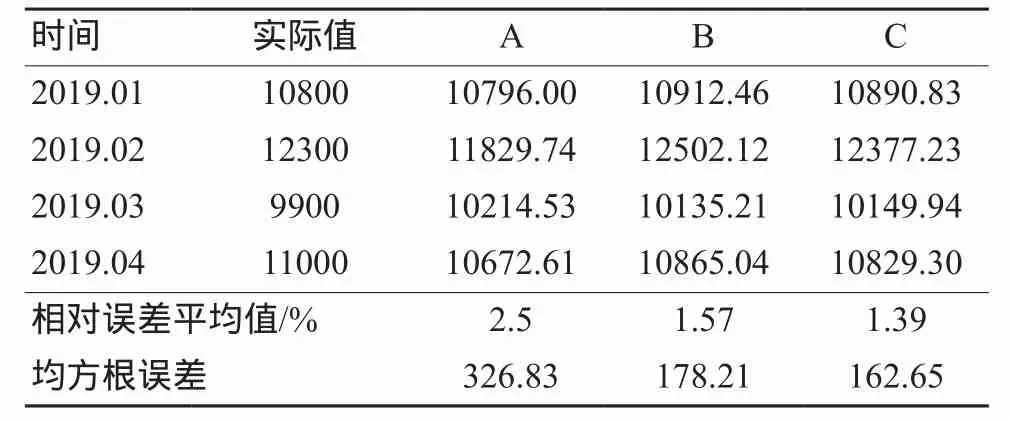
表4 组合预测模型预测结果（支）

从表4中可以看出，相较于单一的预测模型，组合预测模型的预测准确度得到了大大的提升。三种组合预测模型的相对误差均值都远小于5%，其中方差倒数法确定权重的组合预测模型与实际需求数量的均方根误差为162.65，相对误差均值仅为1.39%，与实际需求数量几乎一致，所以组合预测模型适用于低值医用耗材的库存需求预测。

3 讨论与结论

针对低值医用耗材需求提交月计划时存在环节多、主观因素影响大和效率低等问题，本研究提出利用由二次指数平滑预测模型和灰色马尔科夫预测模型组合得到的组合模型来预测次月的医用耗材需求。

本文通过变异系数法、简单加权法和方差倒数法这三种模型权重确定方法，分别得到三种组合模型。三种组合预测模型分别预测了浙江某三甲医院2019年1—4月的20 mL一次性使用无菌注射器的需求量。预测结果显示，三种组合预测模型的相对误差值均小于5%，并且其均方根误差远小于二次指数平滑预测模型和灰色马尔科夫预测模型预测结果的均方根误差，这表明组合预测模型在医用耗材需求预测中有较高的可行性。三种组合模型中，由方差倒数法确定单一预测模型权重的组合模型相对误差均值最小，其可行性最高。

国内外对于医用耗材预测的方法主要有线性模型与非线性模型，此外模糊理论和灰度理论也有应用。在线性模型预测中，许亮业等[17]进行了ARIMA模型在医用低值耗材需求预测的研究，使用自回归积分滑动平均的方法，能够准确地进行医用低值耗材的短期预测，并将其应用于医院物资管理信息系统中。但其构建模型需要的历史数据量大，且模型预测的误差较大。在非线性模型预测中，Xu等[18]提出支持向量机模型进行医疗设备数量预测，该模型预测效果优异，但核函数、参数的选择以及惩罚参数等额外参数需要根据经验进行设定，无特定理论支撑，且庞大算法存在高时耗、低功效的问题。Foucade等[19]使用灰度理论模型进行医疗需求预测，但预测结果存在预测滞后性和拐点误差大等问题。

将本文研究的组合预测模型与上述模型进行比较，对比自回归积分滑动平均法，其使用了8年的历史数据进行预测，预测的绝对误差为8.58%[17]；本文提出的模型使用了两年的历史数据即可进行精准地预测，预测的绝对误差最优为1.39%。对比支持向量机模型，本文提出的模型不需要额外的核函数参数、惩罚函数参数等参数，且无需进行大量复杂的运算即可得出结果，预测精度也与之相近。综合上述分析，本文提出的组合预测模型具有历史数据依赖少，计算量小，具有高预测精度的优点。

当然，由于低值医用耗材种类繁多并且外部影响因素多变，并不是所有低值医用耗材都适用于本文探讨的预测模型。本模型适用于需求量大，且用量随时间变化相对稳定的低值医用耗材。针对需求量小并且需求量波动较大的低值医用耗材来说，本模型并不完全适用。接下来，将本文提出的模型对外科医用口罩、医用消毒液、垫单、输液管等低值医用耗材进行持续跟踪预测，进一步验证模型的有效性。