车辆随机停放对停车楼抗震性能的影响

周潇凡，王宪杰，龙诗琪，杨思昭，王 希，董艳秋，吕 龙

(云南大学 建筑与规划学院，昆明 650500)

随着我国经济的快速发展，私人汽车的拥有量以每年1000万的速度快速增长[1]。根据2019版的《中国汽车工业年鉴》，到2019年底，全国私家车总量接近2亿辆，全国平均每百户家庭拥有超过40辆私家车，在北京、深圳等经济发达的区域，每百户家庭拥有私家车超过70辆。由于私家车的普及停车问题也随之而来，尤其是在寸土寸金的大城市，受土地和停车场数量的限制，许多城市开始兴建大型立体停车楼来缓解城市停车压力。然而在以往的停车楼设计中，大多以层间位移角为限制进行结构的抗震设计，事实上受车辆随机停放的影响，停车楼结构在遭遇罕遇地震时发生扭转破坏的可能性要更大。

考虑随机结构与随机地震激励的分析在过去几十年已经取得重大进展，形成了以李杰[2-5]等研究、发展而来的概率密度演化理论(简称PDEM)。概率密度演化理论可以求解物理量(包括位移、速度、加速度、变形等)的概率密度函数及其演化过程，从三维角度分析该物理量随时间的变化过程[6]。相较于传统的随机结构分析方法，如FPK方程(Fokker Planck Kolmogorov equation)、功率谱分析与矩演化方法[7-8]等，概率密度演化方法具有计算精度高，计算量小，能够在较短的时间内完成对结构的准确分析，从而满足结构精细化、效率化的抗震分析与设计要求[9-10]。

本文基于概率密度演化理论，分别对考虑车辆随机停放和考虑满载时的典型层层间扭转角、层间位移角的概率密度曲面进行对比分析。并基于极值分布的首次超越破坏可靠度分析方法求解停车楼结构的体系可靠度，得出结构的破坏概率矩阵，从而实现预测立体停车楼在遭遇罕遇地震作用时随机车辆荷载对停车楼结构抗震性能产生的影响，为未来高烈度设防区立体停车楼的抗震设计和震后评估提供更加科学的设计方法与思路。

1 考虑车辆随机停放的密度演化方法分析

1.1 车辆随机停放和随机地震荷载下结构动力方程

由结构动力学的知识可以知道，一个n自由度系统的动力方程表示如下：

(1)

将车辆荷载在停车楼中的随机分布等效为质量块，并以随机离散矩阵方式加入到结构质量矩阵中，即将随机车辆质量离散的数学表示式为

Ms=diag[m1,m2,…,mi,…,mn],i=1,2,…,n

(2)

式中：mi为第i层的随机汽车质量；Ms为n×n阶的汽车质量随机矩阵；diag[]为矩阵对角化。

mi=sum(mmaxrand(1,t))

(3)

式中：t表示第i层有t个标准区间；mmax为每个标准区间的最大停车荷载值。

对式(3)中rand命令生成的随机数列进行离散化

bi-1≤ai≤bi,i=1,2,…,t,t≥1

(4)

式中：ai为rand命令生成的第i个数；0≤bi≤1且bi的取值与车的质量有关，则令

ai=bi-1

(5)

因此带有随机停车荷载的运动方程可表示为

(6)

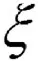
(7)

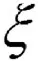
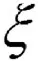
(8)

其中Z1为层间位移角，Z2为层间扭转角，则其物理速度方程可以表示为

(9)

1.2 概率密度演化方程求解

根据概率守恒原理，考虑随机汽车荷载和随机激励下结构的广义概率密度演化方程为

(10)

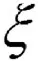
初始条件为

PZΘ(z,θ,t)|t=0=δ(z-z0)PΘ(θ)

(11)

式中：δ(·)为狄拉克函数；PΘ(θ)为Θ的联合概率密度函数；z0为初始值。

将式(9)带入式(10)并结合式(11)，对式(10)进行求解时，采用双边差分法[4]得到Zl(t)的概率密度函数PZl(z,t)为

(12)

式中：ΩΘ为Θ的分布区域。

1.3 数值计算方法

采用数值方法计算概率密度函数时，首先要进行概率密度选点[5]，即在随机向量Θ的分布空间ΩΘ取得一系列离散代表点，记为

θq=(θ1,q,θ2,q,…,θs,q),q=1,2,…,nsel

(13)

式中：nsel为取得离散代表点的数目，离散点的数目与随机变量的数目有关[11]。

同时确定每个点的赋得概率

(14)

式中：Vq为代表性体积。

通过有限元软件分析并结合初始条件求解每组θq下的PZΘ(z,θq,t)值，将所有值求和即可得到Pz(z,t)的数值解

(15)

2 结构体系可靠度求解

基于极值分布的首次超越破坏问题动力可靠度等价于具有无穷多个单元数串联系统的可靠度问题[12-13]，即

(16)

式中：R为结构体系的可靠度；Xi为各层的层间位移角或层间扭转角；bi为层间位移角或层间扭转角的约束条件。

当bi不相同时，表明存在多个动力失效模式，在这种复杂失效准则面前，可以通过构造等价极值事件，将结构整体可靠度问题转化为等价极值概率密度函数的一维积分问题，相对于多维积分而言，不仅减小计算量，降低分析难度，且结构可靠度分析精度较高。结构的整体可靠度公式如下：

(17)

式中：τ是虚构的虚拟时间。

此时可以构造等价极值

(18)

至此式(16)中的整体可靠度转化为

(19)

3 工程运用

以云南省大理市某一立体停车楼的设计为例，主体结构为10层的钢混结构。结构首层层高为3.6 m，2—4层层高为2.55 m，5—8层层高为2.15 m，9层层高为2.6 m，10层层高为2 m。设防烈度为8度(0.2g)，场地土类别为Ⅱ类，设计地震分组为第三组，地面粗糙程度为B类。结构所用的主要材料是钢材Q235、混凝土C30。除第1层柱、第10层楼底和楼顶用钢筋混凝土浇筑外，其他结构都是钢结构。该停车楼通过盈建科软件建立模型后，结构的标准层如图1所示，通过盈建科接口程序将停车楼模型导入到ABAQUS，得出模型如图2所示。输入20条天然波并调幅到4 m/s2(大震)，分别计算考虑随机汽车荷载和考虑满载，停车楼结构的动力响应和可靠度。

图1 标准层

图2 停车楼模型

3.1 考虑汽车荷载的停车楼有限元模型

考虑在停车楼的2—9层进行随机车辆荷载的布置。将停车楼每层划分为8个标准区间，如图1所示，每个长方形(长宽分别为7.3和4.82 m)为1个标准区间，每个标准区间有3个车位，每个标准区间的中心作为随机汽车荷载的作用点。通过查阅《中国汽车工业年鉴》可以知道，我国居民通常驾驶私家车的最小质量以长安汽车-悦翔低配为例，车质量为1080 kg；最大质量以丰田-汉兰达高配为例，车质量为2070 kg。因此在该长方形上作用的车辆荷载可能为0或者1080～6210 kg，采用rand命令随机生成的8个数，经过离散化后随机分布到每个标准区间中。因此在停车楼结构的每次有限元分析中都将随机生成一系列与上次不同的停车荷载，这样就可以较好地考虑汽车随机停放荷载对停车楼结构抗震性能造成的影响。

3.2 停车楼结构破坏状态与量化指标

根据《建筑抗震设计规范》(GB 50011—2010)中的结构破坏状态与相应指标[14]，轻微破坏、中等破坏、严重破坏、倒塌对应的层间位移角限值如表1所示，各个破坏状态下层间位移角与层间扭转角的关系由文献[15]可知

表1 结构不同破坏状态及其判别标准

(20)

式中：αLS为各个破坏状态下的层间扭转角；θLS为各个破坏状态下的层间位移角；h为层高；R为构件到结构刚心的最大距离；u为最大层间位移与平均层间位移的比值。

由式(20)可以得到停车楼结构的破坏状态与其最大层间扭转角的关系，如表2所示。

表2 层间扭转角量化指标 rad

3.3 停车楼动力响应

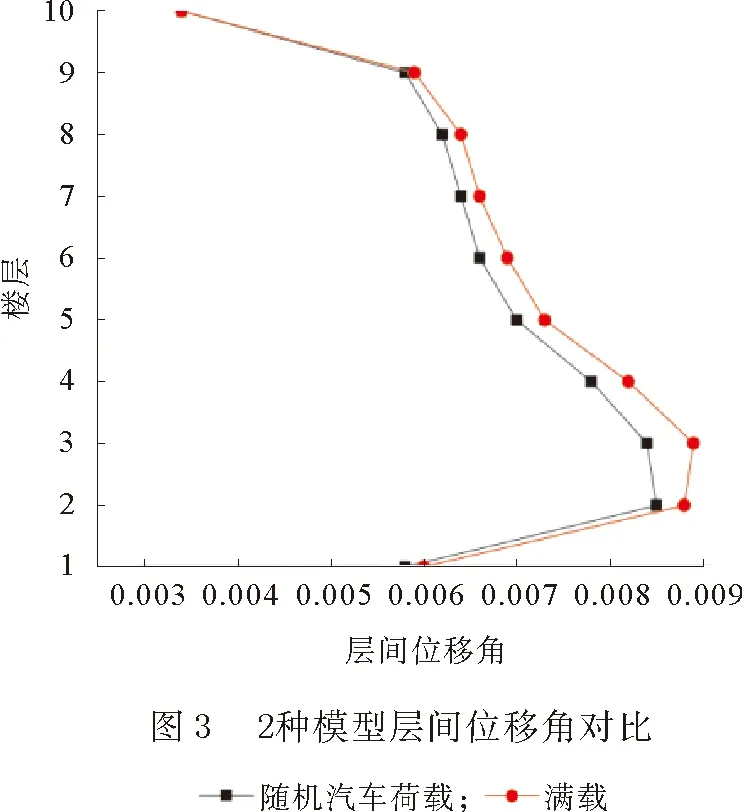
考虑随机汽车荷载(模型1)的各层最大层间位移角与考虑满载(模型2)的各层最大层间位移角如图3所示，从图中可以知道考虑随机停车汽车荷载后，结构的最大层间位移角出现在第2层,为8.5×10-3，且比考虑满载时的第3层层间位移角减小了4.49%，2种模型的最大层间位移角均小于规范给定的结构倒塌时的极限值0.02。2种模型的层间扭转角如图4所示，考虑随机汽车荷载后停车楼结构的最大层间扭转角出现在第1层,为9.421×10-4rad,考虑满载的停车楼的最大层间扭转角出现在第9层,为8.943×10-4rad，前者比后者增大了5.34%，前者比后者更加逼近该结构倒塌的层间扭转角极限值1.04×10-3rad。最大层间扭转角变大是由于停车荷载的随机分布，导致停车楼结构整体质量分布不均匀。因此停车楼结构在遭遇大震时发生层间扭转破坏的可能性显著提高。由于层高的突变导致2种模型的层间扭转角在第9层形成了局部极大值。在以层间位移角为判别指标时，结构进入塑性状态，但离倒塌尚远；以层间扭转角为判别指标时，考虑车辆随机停放后，该结构面临倒塌的风险，结构的薄弱层由考虑满载时的第9层转移到第1层。

停车楼结构考虑随机汽车荷载和考虑满载的典型层的第1层层间扭转角、第3层层间位移角的概率密度曲面如图5所示，典型时刻的概率密度曲线如图6所示。因概率密度演化理论能够直接给出层间扭转角的瞬时概率密度函数以及层间扭转角的演化过程，通过对比图6可以发现，考虑随机汽车荷载相对于考虑满载层间扭转角的概率密度曲线在7.70或7.90 s时要更“胖”，而2种模型层间位移角的概率密度曲线在7.65或7.90 s时变化不大。说明了停车楼在遭遇罕遇地震时考虑随机停车荷载后，层间扭转角相比于层间位移角受到的影响更大。

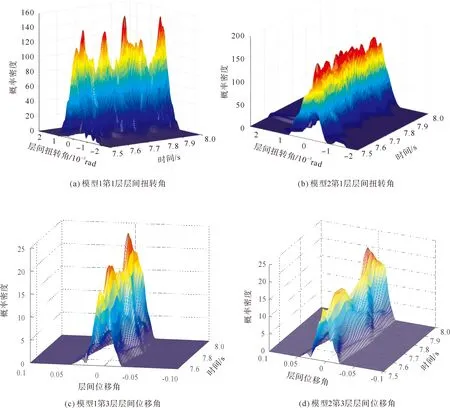
图5 2种模型动力响应概率密度曲面

图6 2种模型典型时刻的概率密度曲线

3.4 停车楼结构的整体可靠度

3.5 破坏概率矩阵

由表3可以预测结构在遭遇大震作用时，即PGA(地震峰值加速度)为4 m/s2时，结构可能发生不同破坏状态的破坏概率如表4所示，从表中可以知道2种模型在遭遇罕遇地震作用时基本完好的概率分别为5.22%和2.27%；稍加修理就可使用的概率为3.74%和7.38%；需要一般修理，采取安全措施方可使用的概率为5.96%和34.76%；应排险大修，并局部拆除的概率为75.9%和55.59%；倒塌的可能性为9.18%和0。停车楼模型在考虑随机汽车荷载后遭遇大震时可能受到基本完好、严重破坏、倒塌的概率提高，受到轻微破坏、中等破坏的可能性降低。由《建筑抗震设计规范》(GB 50011—2010)可知结构在发生严重破坏或倒塌时对生命造成威胁，考虑随机汽车荷载和考虑满布汽车荷载的停车楼结构受到严重破坏和倒塌的概率分别为0.8508和0.5559。因此未考虑随机汽车荷载时停车楼结构在发生大震时实际上低估了地震对生命造成的威胁。

表3 2种模型下结构的可靠度

表4 2种模型的破坏概率矩阵

4 结论

本文基于概率密度演化理论同时考虑到地震的随机性与车辆随机停放的复合随机过程，对某一实际立体停车楼进行时程分析，评估随机地震激励、随机汽车停放对钢混结构停车楼抗震性能产生的影响，并得出以下结论：

1) 考虑随机汽车荷载后，停车楼结构的薄弱层存在转移的可能性。因此车辆随机停放对结构薄弱层的分布产生一定的影响。

2) 考虑车辆随机停放后，结构各层的层间扭转角的瞬时概率密度曲线明显变“胖”，表明停车楼结构在遭遇大震作用时的扭转响应显著变大；而层间位移角的概率密度曲线变化不大，说明考虑车辆随机停放后，层间扭转角起主要控制作用。

3) 停车楼结构考虑满载并以层间位移角为可靠度指标时停车楼结构不会倒塌，考虑车辆随机停放并以扭转角为指标时，结构有9.18%的概率倒塌。因此在停车楼的设计中要考虑车辆的随机停放，并通过层间扭转角进行结构可靠度计算。