拱顶背后空洞对直墙式隧道结构安全性影响分析
2021-09-03车增军张素磊陈立平陈德刚
鲍 彤,车增军,张素磊,,*,陈立平,陈德刚
(1.青岛理工大学 土木工程学院,青岛 266033;2.青建集团股份公司,青岛 266071)
目前我国交通基础建设处于高速发展阶段,运营隧道里程不断增长,交通运输部2019年统计数据表明,我国已修建的公路隧道达19 067座,运营里程达18 967 km,其中,特长隧道1175座,总里程5218 km;长隧道4784座,总里程8263 km[1]。随着隧道数量的不断增加,运营隧道的安全问题也引起了工程界相关技术人员的重视。衬砌背后空洞作为隧道常见病害形式之一,会直接影响衬砌围岩间力学性能,改变隧道周边岩体应力分布,进而引起围岩松弛破坏,严重时甚至诱发隧道失稳、塌方[2];张顶立等[3]对100余座铁路隧道进行调研后发现,衬砌背后存在空洞和松散区占比高达11.56%;张素磊等[4]对160余座公路隧道进行了无损检测,结果表明存在1649处衬砌背后空洞,且主要位于拱部位置;刘昌[5]对100余座公路隧道无损检测结果统计后发现,衬砌脱空主要位于拱顶及拱腰处,占比高达95%。以上实例结果表明拱顶背后空洞在隧道工程中的普遍性。鉴于此,专家学者们纷纷对此展开研究。YASUDA等[6-7]通过理论计算,得出了隧道存在空洞情况下的二维弹性解;黄宏伟等[8]通过有限元软件,探究了衬砌背后空洞条件下裂缝的扩展过程及形成机制;孙铁军[9]、傅鹤林[10]等采用荷载-结构法,分析了不同类型衬砌缺陷条件下隧道结构安全性的变化规律;闵博等[11]通过数值模拟研究了连拱隧道在背后空洞条件下衬砌渐进破坏过程,并通过模型试验加以验证;张旭等采取模型试验分析了拱顶存在双空洞条件下,衬砌结构的损伤过程和结构受力状态[12-13];车增军采用扩展有限元研究了空洞条件下衬砌开裂机理[14]。现有的研究成果对后续研究有着重要的参考价值,但现有的成果中以直墙式隧道为对象的空洞病害下安全性研究很少,且在数值模拟过程中,模型以二维有限元模型为主,将空洞视为纵向无限延伸,而在实际隧道工程中空洞纵向长度有限,因此二维模型不能合理地反应衬砌受力状态。本文以某工程2车道直墙式隧道为背景,针对拱顶背后存在空洞工况,建立三维数值模型,研究衬砌结构内力和安全系数的演变过程,研究成果可为直墙式隧道衬砌结构病害治理提供参考。
1 计算模型
以某工程Ⅴ级围岩2车道直墙式隧道为计算模型,隧道结构横断面及计算模型如图1所示,计算模型中围岩满足M-C屈服准则,二次衬砌为C30模注混凝土结构,其厚度40 cm,各项材料力学参数见表1。

图1 计算模型

表1 材料力学参数
2 计算方案
靳学峰[15]、刘海京[16]等研究了当隧道衬砌背后存在不同形状空洞时,衬砌的受力状态和变形的规律,研究结果表明:衬砌背后空洞形状对隧道结构受力影响较小。鉴于此,为了使研究便于分析,将脱空形状简化为环形,两者相互位置关系如图2所示。
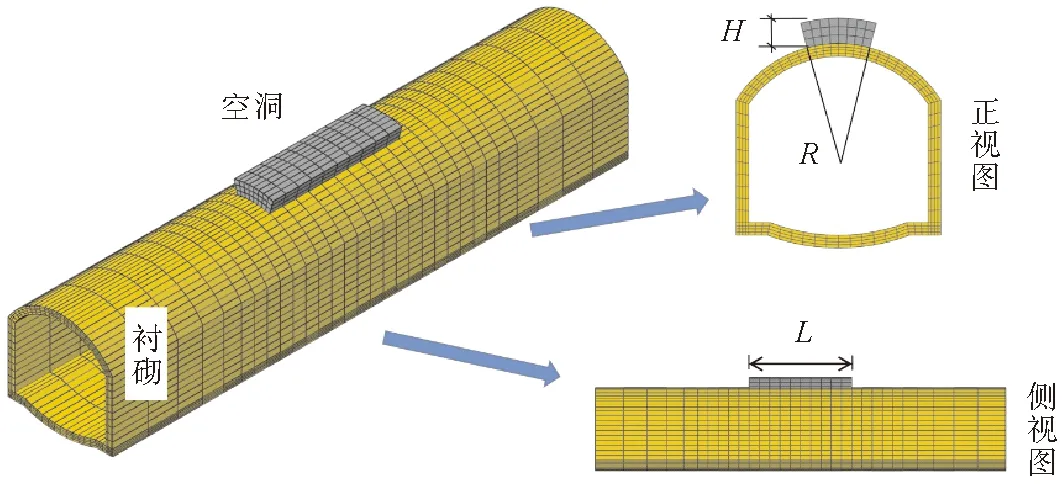
图2 衬砌与空洞相互位置关系
参考张素磊等[4]对公路隧道衬砌背后空洞的统计数据,就空洞的竖向高度、环向范围、纵向长度对衬砌安全性影响规律进行计算分析,计算工况见表2。

表2 计算工况
3 三维数值计算结果分析
为研究空洞不同尺寸对衬砌结构安全性的变化规律,首先对无空洞工况下衬砌结构内力进行分析。图3为无空洞工况下衬砌应力云图。由图3可见,隧道墙角以及拱肩位置应力集中现象较为明显,在拱部内侧及仰拱内侧承受拉应力。
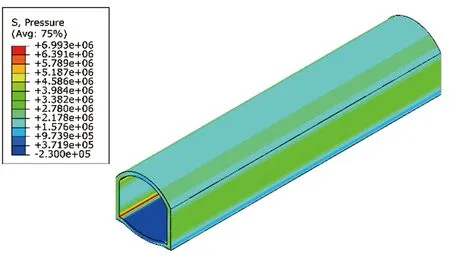
(a)衬砌应力
参考《公路隧道设计规范》(JTG 3370.1—2018),获取衬砌结构安全系数,选横截面上10个特征点进行分析,在无空洞工况下,计算得到衬砌轴力、弯矩、安全系数分布规律如图4所示。可见,衬砌结构轴力在边墙位置大于拱部及仰拱位置。从图4(b)可见,衬砌结构在拱部、边墙及仰拱位置承受负弯矩(弯矩为负代表受压,反之为拉),就弯矩绝对值而言,拱肩、拱脚位置最大且应力集中。从拱部至拱脚,安全系数表现为先降低后增大。

图4 无空洞工况下衬砌内力分布与安全系数
3.1 空洞环向范围
本节对衬砌存在不同环向范围空洞展开研究,计算模型如图5所示,其中空洞高度H为20 cm,长度L为10 m。

图5 计算工况
选取横截面上10个特征点对衬砌各位置轴力、弯矩值进行分析。图6为不同环向范围空洞下衬砌内力分布。对比可见,随着环向范围R的增大,1—7号特征点轴力逐步变小,而8—10号特征点轴力值小幅度增加;空洞环向范围R=60°时,1—4号特征点轴力值大幅度降低。由分析可见,当空洞环向范围R增大时,隧道拱部位置的衬砌弯矩值发生显著变化,对比图4(b),由于存在空洞,导致空洞处衬砌由正常工况下的内侧受拉变成外侧受拉,衬砌弯矩值也从负值变为正值,当R=45°时,1号特征点的弯矩值达到峰值163.2 kN·m,相比于R=15°时,增大了145.7 kN·m。
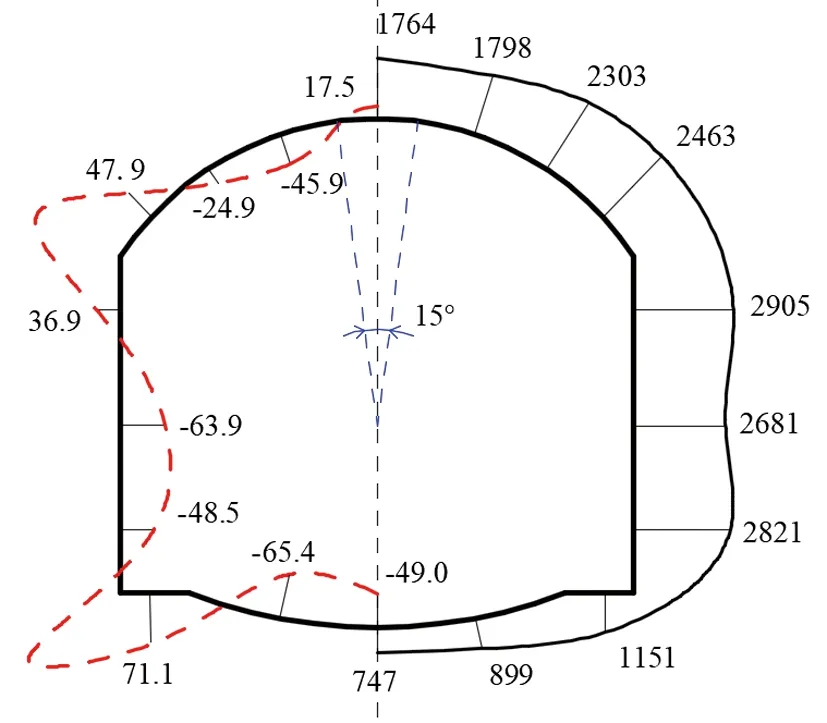
(a) R=15°
衬砌结构内力曲线分布如图7所示。由图可见,当空洞环向范围逐步增大时,1—5号特征点的轴力发生显著变化,当R=15°时,衬砌1号特征点轴力相比于正常工况下的轴力小幅增加,其余部位呈现小幅降低;当空洞环向范围继续增大时,衬砌1—6号特征点的轴力大幅降低,但边墙5—7号特征点轴力呈微弱降低趋势,其中,仰拱8—10号特征点轴力稍有增大。随着空洞环向范围增大,1号特征点弯矩由负值变为正值。当R为15~30°时,1号特征点弯矩变化最大;而3号特征点弯矩值呈现不同的特征,当空洞环向范围增大,不断负向增大,3号特征点弯矩值在R为30~45°时变化幅度最大。与1—4号特征点相比,5—10号特征点弯矩值基本不受空洞环向范围增大的影响。
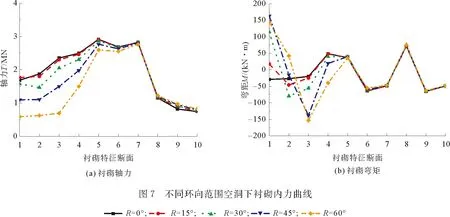
图8为不同空洞环向范围下衬砌安全系数曲线。可见,拱部1—4号特征点受空洞环向范围影响较大,边墙5—7号特征点衬砌安全系数基本不变,而仰拱8—10号特征点衬砌安全性小幅降低。其中,2,4号特征点安全系数增大;1,3号特征点安全系数,当R由30°继续增大时,安全性显著降低。
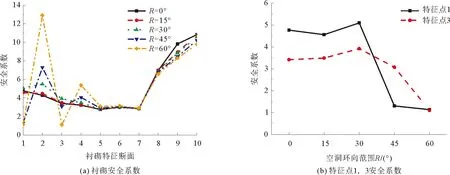
图8 不同环向范围空洞下衬砌安全系数曲线
3.2 空洞纵向长度
本节对衬砌存在不同纵向长度空洞展开研究,其中空洞高度H为20 cm,环向范围R为45°,各特征点内力如图9所示。可见,随着纵向长度增大,衬砌拱部特征点弯矩及轴力变化较大,L=5 m时1号特征点衬砌弯矩为76.8 kN·m,当L≥10 m时1号特征点衬砌弯矩增至163.2 kN·m,增幅达112.5%,轴力呈微弱增大趋势,空洞纵向长度增大使得隧道拱部位置受力更加不利。
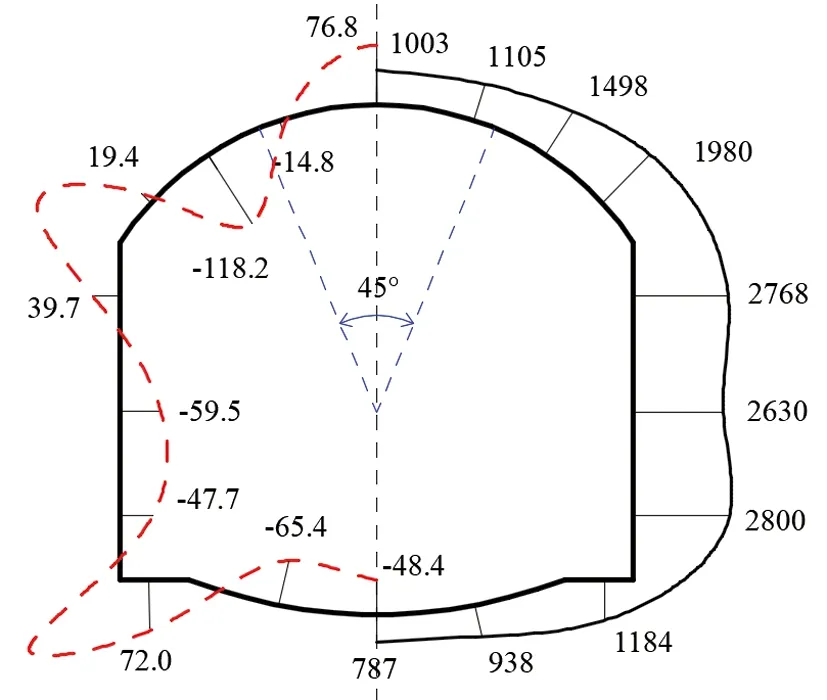
(a) L=5 m
图10为存在不同长度空洞时衬砌结构内力曲线分布。可见,受空洞影响,1—4号特征点的轴力及弯矩均发生明显变化,然而,当L继续增大时,1,2号特征点轴力出现显著变化,而5—10号特征点受力性能基本不发生改变。
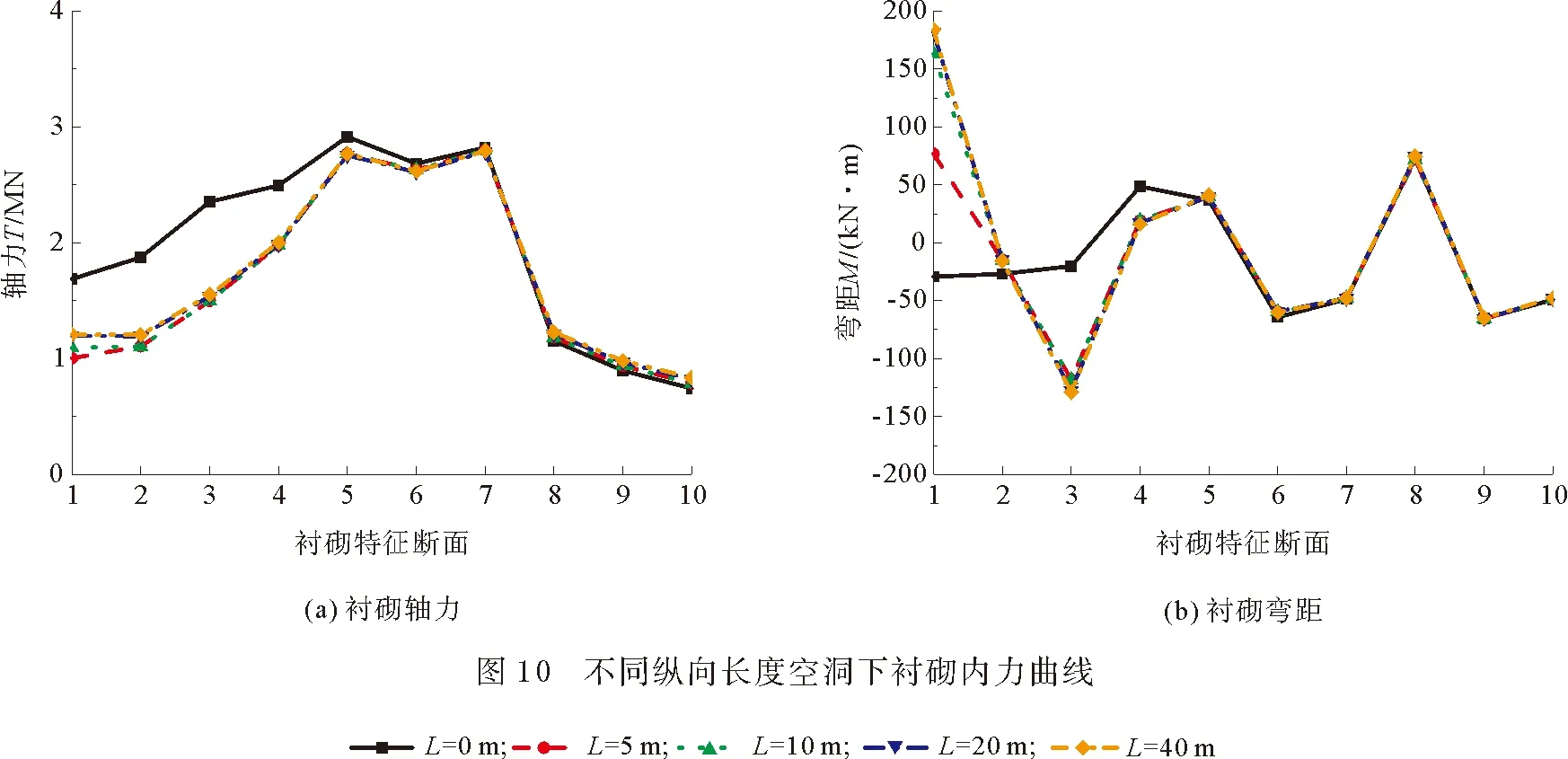
图11为空洞不同纵向长度下衬砌安全系数曲线。可见,1—4号特征点安全性受空洞纵向长度影响较大,而边墙及仰拱位置衬砌结构安全性受空洞纵向长度影响较小。1号特征点安全性表现为:L增大,安全性先是升高,而后持续降低,当空洞长度L从5 m增大到10 m时,1号特征点安全系数急剧变化,降至1.19,当L由10 m继续增大时,其安全系数仅小幅度降低。
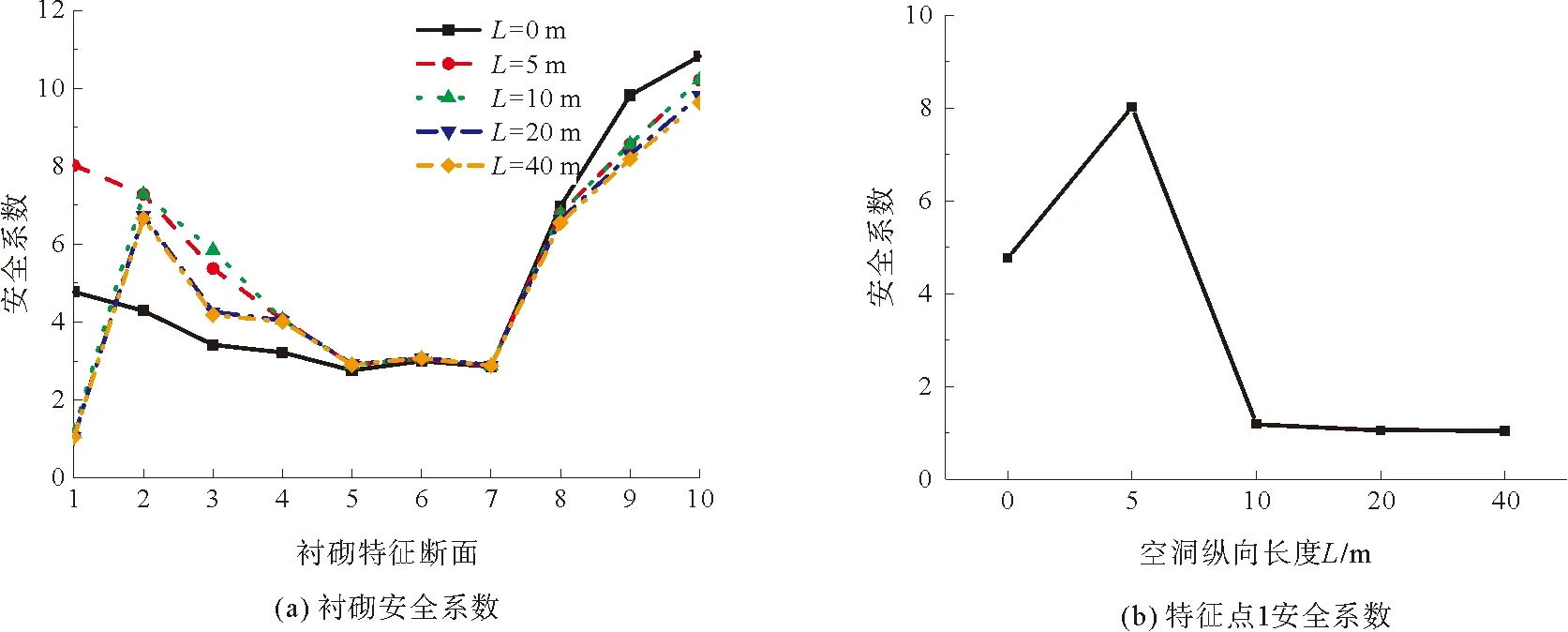
图11 不同纵向长度空洞下衬砌安全系数曲线
3.3 空洞竖向高度
本节对衬砌存在不同竖向高度空洞展开研究,其中空洞环向范围R为45°,长度L为10 m。图12为存在不同竖向高度空洞时衬砌结构内力曲线分布。由于存在空洞,1—7号特征点轴力发生不同幅度的降低,而8—10号特征点稍有增大。由图12(b)可以发现,由于存在空洞,1—4号特征点弯矩值发生明显变化,5—10号特征点弯矩值变化很小。其中,由于存在空洞,导致1号特征点从负弯矩变成正弯矩,当空洞径向高度增大,弯矩值变化幅度降低;由于存在空洞,导致3号特征点的负弯矩值出现增大。由上分析可见,衬砌内力及弯矩值受空洞竖向高度H影响较小,并不会引起结构上内力的分布规律发生改变。
图13为不同竖向高度空洞下衬砌安全系数曲线。由于存在空洞,1—4号特征点安全系数发生显著变化,但是随着空洞竖向高度继续增大,各特征点安全系数变化幅度降低。由于存在空洞,1,3号特征点的安全系数降低,当空洞竖向高度继续增大,3号特征点安全系数持续降低,仰拱位置8—10号特征点安全系数发生小幅度降低。由以上分析可知,当径向高度H发生改变时,衬砌结构安全性变化不明显。1号特征点内力变化最为明显,以此为例,对衬砌存在空洞时结构安全性变化规律作进一步研究,可见1号特征点安全系数由正常工况下的4.766降至1.187,而当H继续增大时,安全系数仅小幅度降低,可见,当径向高度H继续增大时,1号特征点安全系数的降低幅度趋于平衡。
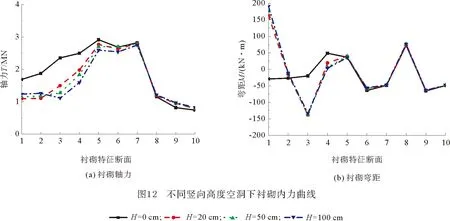
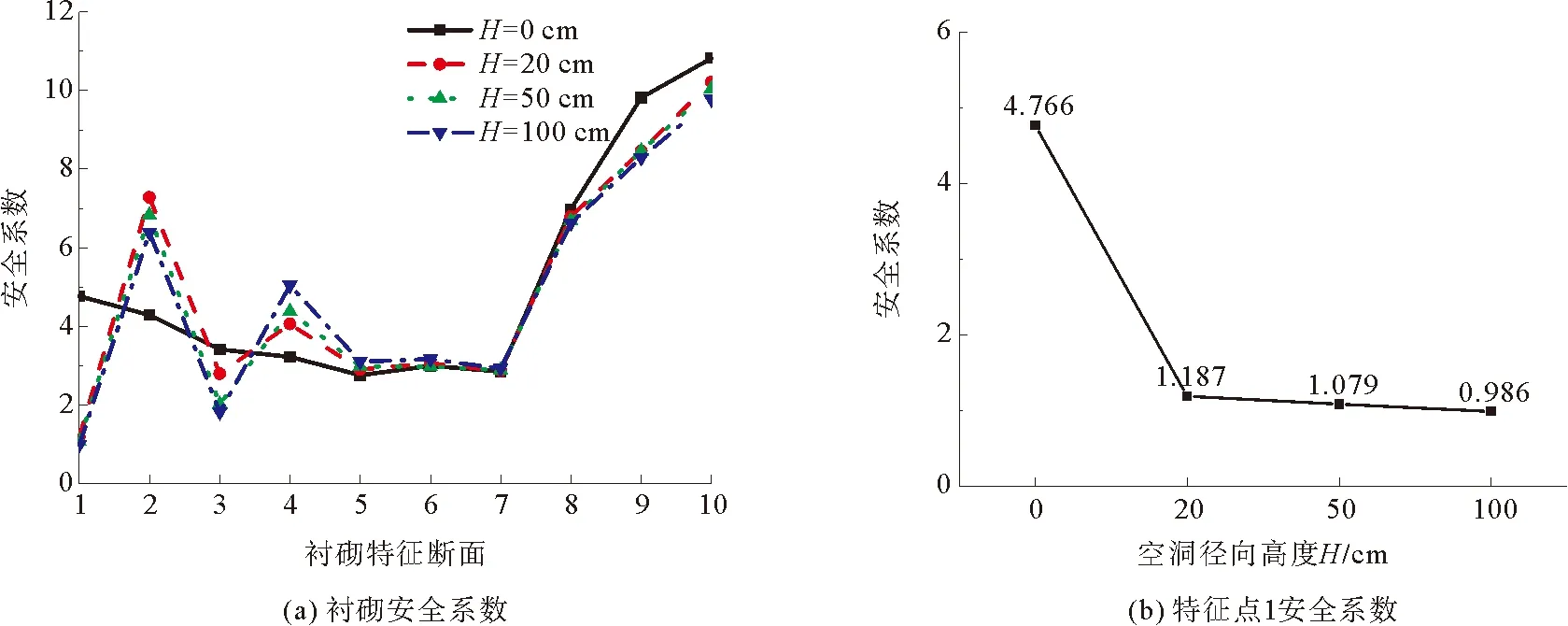
图13 不同空洞高度衬砌安全系数曲线
4 结论
1) 拱顶位置存在空洞,改变了衬砌结构内力分布规律,使得空洞范围内衬砌结构由外侧受压转变为外侧受拉,大幅度降低了衬砌结构整体安全性。
2) 空洞环向范围的增大,显著改变了衬砌结构内力分布规律,使得空洞范围内衬砌由受压状态转变为受拉状态,当空洞环向范围大于30°后,衬砌整体安全性急剧降低。
3) 随着空洞纵向长度的增大,拱部衬砌结构轴力及弯矩出现不同程度的增大现象。当空洞长度L从5 m增大到10 m时,拱顶位置安全系数降至1.19;但是当空洞长度大于10 m后,空洞长度的继续增大,结构安全性仅小幅度降低。
4) 相比于空洞环向范围及纵向长度的变化,空洞竖向高度的增大基本不改变衬砌结构内力分布规律,隧道结构安全性变化不大。因此,在实际工程中,应重视空洞环向范围及纵向长度的变化对隧道结构安全性的影响。
