指向理性思维培育的活动设计
2021-09-03于蓉
○于蓉
(作者单位:江苏省扬州市育才小学东区校)
教学中,学生借助于某类事物的感性材料进行比较、归纳和初步抽象活动,并未能实现对事物间内在联系的理性认识。随着认识的不断深入,需重视深层的理性思维活动,引导学生逐渐把握事物间的内在联系,发展思维能力。数学活动,是小学生理性思维培育的重要外在形式。
指向理性思维培育的活动设计,应遵循数学活动设计的要求,进行学情调研、分析教学内容,开发活动资源,丰富活动材料,将活动目标转化为问题,寻求符合儿童学习生活特点的情境,发挥数学学科对于培育学生理性思维的价值。
一、在核心处设计,凸显概念本质,引发求真意识
高斯曾经指出:“在数学中重要的不是符号,而是概念。”教师应厘清知识点中核心的概念是什么,核心概念的本质属性是什么,再通过设计活动让学生感悟概念的丰富内涵。
【教学案例】在《认识垂线》这一课中会出现垂线、垂直线段、距离、垂足、互相垂直等较多知识点,教师在教学中一般是讲完垂线,再讲垂直线段、垂直,接着认识距离,熟记每段文字的内容,学生学得是百无聊赖。
【问题分析】一节课有较多知识点时,如果纠缠于每个知识点的具体内容,必然是咬文嚼字,远离数学学科的育人目标。在认识线段时,学生已知两点之间线段的长度是两点间的距离,本节课是点到直线的距离,将问题进行转化,在直线上找到一个点,这两点间的线段长度就是点到直线的距离。这个点怎么找,就成为学生探索的目标。
【活动设计】
活动目标:点P到直线的距离是多少?
活动材料:在一个点上固定一把尺,尺可以绕固定点旋转。
活动步骤:1.在点P外画一条直线,在直线上点几个点,并分别连接点P。
2.猜一猜:哪条线段最短?再验证一下,它真的最短吗?
3.想一想:这条线段是特殊而唯一的吗?
4.说一说:点P到直线的距离是多少?说说你的理由。
活动中,学生用可以转动的直尺量出每条线段的长度,并且在转动中感受到垂直线段具有特殊性与唯一性,因此给予特别命名。在此基础上再来认识垂足与距离,学生较容易接受和理解概念的内涵。
围绕概念本质设计活动,需要教师将具体内容进行提升,成为指向本质概念的问题,从而发挥聚合作用,将零散的、孤立的知识点整合起来,促进学生的理解,引导学生求真。
二、在联结处设计,丰富思考视角,引发求联意识
数学知识是一个不可分割的整体,各个部分之间相互联系。根据数学知识结构体系和学生已有的认知基础设计数学活动,便于学生形成整体分析的视角,发挥这部分内容的育人价值。
【教学案例】在《分数乘分数》的教学中,教师常借助图形帮助学生理解分数乘分数的计算规则。但一个班级的学情检测数据表明,学生并未真正理解算理。
班里一共42名学生,有35人都不知道怎么写,只有7人能画出正确的结果。
问题二:你知道为什么分数乘分数时用分母相乘的积作分母吗?
【问题分析】从“后测”可以看出,学生知道积的分母、分子与乘数的分母、分子的对应关系,但并未理解“为什么可以这样做”。一是教材中都是真分数与真分数相乘的直观模型,未涉及真分数与假分数相乘的直观模型,学生对分数乘分数的理解具有局限性;二是学生还没有将分数乘法与整数乘法的算理建立联系。
【活动设计】在《分数乘分数》的练习课中进行整体设计。
活动一:计数单位相乘,会怎样呢?
10×10 1×1 0.1×0.1 0.1×0.01
学生计算后交流,计数单位相乘,结果有可能变大,也有可能变小。
思考:分数单位相乘会怎样呢?画一画,想一想。
活动二:算一算,比一比,有什么发现?
活动三:比一比,说一说可以怎样比较?
a×b○a
整数乘整数、小数乘整数、分数乘整数的计算一直是合并与累加的过程,本质上仍是连加的计算。活动中引导学生发现分数乘分数就是先求出计数单位是多少,再求有多少个这样的计数单位,使学生体悟到整数、小数、分数计算规则的一致性。活动三是让学生进行分类思考,在比较中清晰地认识到整数、分数的计算规则具有一致性,但也具有各自的特点。
联结处不仅是在数学内部寻找,还应在数学与其他学科、生活、学生的已有经验中寻找,在求联中感受数学的统一与和谐。
三、在易错处设计,促进深度理解,引发求证意识
学生的易错处是数学活动设计中需考虑的问题之一,教师应注意收集、分析原因,并根据学生年龄特点设计活动,有助于学生对学习内容有深入的理解,并在问题解决中有清晰的思路。
【教学案例】如图,比较图形①和图形②的周长时,有近一半的学生认为图形②的周长更长。即使在教师干预后,也有近30%的学生并不认可教师的观点。
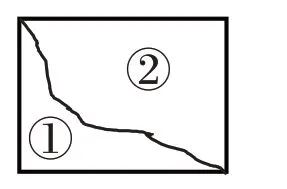
【问题分析】平面图形的周长与面积是学生容易混淆的概念。周长是围成的平面图形一周边线的长度;面积指图形一周边线围成的平面的大小。两者都和边线有关,学生容易将面的大小与边线的长短相混淆。
【活动设计】
活动目标:画一条线,把长方形分成周长相等的两部分。
活动材料:方格纸上有6个一样的长方形。
活动一:把一个长方形分成两个周长相等的图形。
由于学生认知的局限性,画出的图形都是对称的图形。
活动二:把长方形分成两个周长相等的图形,还可以怎么分?画一画,再说一说。
由于有方格纸,学生可以通过数格子确定图形的周长是多少。学生会看到图形的长和宽没有变,分割图形的这条线段是公共边,不管怎么画,都不会影响两个图形周长的关系。
活动三:连接两个相对的顶点,画出的线把长方形分成的两个图形周长一样吗?说一说为什么?
活动中,学生会逐步打开自己的思维,不再局限于对称的图形周长相等,而是借助于格子数比较周长,在比较中优化比较的方法,在说一说中厘清思考的依据,进一步理解周长的内涵。
因数学的抽象性与儿童认知发展的渐进性、局限性存在冲突,学生在学习中出现错误是不可避免的。教师需关注学生在哪里出错,分析错误的原因,进而设计活动触及认知盲区,使学生逐步形成面对问题时审慎的态度和求证的意识。
四、在常规处设计,提升思维品质,引发创生意识
教师要善于在教学常规中挖掘提升学生理性思维的空间,通过寻求可以设计的活动元素,激活学生的思维。
【教学案例】教学《圆的周长》时,教师会花大量的时间让学生测量、计算,获得圆周率的近似值。课后访谈中却发现,部分学生认为圆周率与3.14是相等的关系。学生不仅对圆周率没有正确的认知,也未感受到圆周率让众多数学家与数学爱好者痴迷的魅力。
【问题分析】学生通过阅读了解到圆周率与3.14有关系,通过测量感悟到圆周率是3多一些。但由于圆周率是无限不循环小数,学生只能看到一部分数字,并未理解圆周率表示的是周长与直径的关系,是一个确定的数。由此,教学中让学生感悟到圆周率是一个确定的数,则成为培育理性思维的一个契机。
【活动设计】
活动一:猜想——圆的周长与直径可能有怎样的关系?
学生形成猜想:圆周长与直径的比值比2大,但比4小,是3多一些。
活动二:验证——圆的周长与直径的比值是3多一些吗?
活动要求:
1.两人合作,测量出所给不同圆的直径和周长,填入表格。
2.用计算器计算出周长除以直径的商(除不尽的得数保留两位小数),并把结果填入表格。
3.根据算出的商写下你的发现。
在学生测量的基础上得出结论:不一样的圆,它们的周长与直径的比值都是3多一些。
疑问:比3多多少呢?测量是有误差的,怎样能让数据更有说服力?
活动三:寻找——数学家用怎样的方法确定圆周率是多少呢?
学生阅读教师提供的资料,并观看视频,了解数学家研究圆周率的方法与历程。
对于圆周率的探索,了解其意义只是目标之一,重要的是在探索圆周率的过程中感悟人类对未知的好奇与探索精神。活动中,引导学生在初步猜想的基础上,通过测量确定猜想的准确性,再去寻求数学家的研究方法,感受数学家的严谨、求真与创新精神,从而激发学生对问题的探索与创生意识。
指向理性思维培育的活动设计,需要教师用心观察学生的学习过程,找到学生学习中的障碍与盲区,将问题与学生经验建立联系;也需要教师深入理解数学内容本身,提炼出核心问题,在此基础上尽可能地寻找符合儿童认知特点的活动背景,提供学习材料,达成学生在活动中积累理性思维经验、提升数学素养的目标。
