双重耗能智能框架摇摆墙结构地震响应对比分析

2021-09-03罗维刚刘纪斌郭易令宋江朋

兰州理工大学学报 2021年4期

罗维刚, 刘纪斌, 张杨, 郭易令, 祁盼, 宋江朋

(1. 兰州理工大学土木工程学院, 甘肃兰州 730050; 2. 兰州理工大学甘肃省土木工程防灾减灾重点实验室, 甘肃兰州 730050)

摇摆墙(rocking wall)[1]是一种墙底具有特殊构造的墙体，墙底约束被放松，在地震作用下可降低上部结构本身的延性需求和破坏，以及减小基础在倾覆力矩作用下的抗拉设计需求.Hitaka、Sakino、Gavidour、冯玉龙、何晴光等[2-5]研究了摇摆体与基础间设置耗能减震装置后结构的抗震性能，结果均表明通过耗能装置的滞回特性耗散能量降低了地震响应.崔浩然、刘迪、Blomgren、曲哲、Barbagallo等[6-11]研究了摇摆结构和主体结构间设置阻尼器后结构的地震响应，该体系减小了地震引起的损伤，促进了震后的快速修复.上述摇摆结构体系都是设置单一的消能减震装置，而吕西林等[12]在第16届世界地震工程大会上对开发摇摆、自复位和可更换等多种技术组合使用的结构新体系提出了展望.

框架剪力墙结构在中国中高层建筑中广泛使用，但是在地震中连梁及剪力墙根部容易发生破坏.基于框架与剪力墙在地震作用下不同变形模式协同工作的原理，在框架与剪力墙之间将连梁更换为耗能单元.本课题组采用了基于滞回耗能的屈曲约束支撑(buckling restrained brace,BRB)[13]作为替换连梁的耗能单元进行非线性动力时程分析，结果表明：当BRB屈服强度和初始刚度控制在一定范围内时，可以有效减小楼板水平峰值加速度，减小结构地震响应，且能在损坏后迅速替换.另一方面，考虑到剪力墙底部容易发生破坏，因此放松墙底约束，形成框架摇摆墙结构，并在墙体底部设置金属阻尼器，以实现墙底耗能和可更换的需求.本次研究在框架剪力墙间设置BRB的智能双重结构体系基础上，放松剪力墙底部约束，并在底部设置耗能单元，进行非线性动力时程分析，研究该新型双重耗能结构体系在地震作用下的受力变形情况以及耗能减震机理.

本次研究以兰州地区某六层混凝土框架剪力墙结构为例，采用ABAQUS有限元软件建立2D模型进行非线性动力时程分析，对比分析传统框架剪力墙结构(模型1)、设置BRB的智能框架剪力墙双重结构(模型2)、底部铰接摇摆墙与框架间连接BRB结构(模型3)和底部连接金属阻尼器的双重耗能机制智能框架摇摆墙结构(模型4)在地震动下的动力响应.研究新型双重耗能单元控制的智能框架摇摆墙结构体系在地震作用下的动力响应以及耗能减震机理.

1 结构模型

1.1 原型结构基本信息

分析模型的原型结构为兰州地区某六层钢筋混凝土框架剪力墙结构，根据GB 50010—2010 《混凝土结构设计规范》[14]设计，平面布置如图1所示.结构首层层高为5.1 m;标准层层高为3.1 m；柱截面尺寸为700 mm×700 mm；梁截面尺寸为300 mm×500 mm；连梁截面尺寸为300 mm×750 mm；楼板厚度为150 mm；设防烈度为8度，场地类别为II类，设计地震分组为第三组，设计基本地震加速度为0.3g，设计基准期为50年.混凝土采用C35，钢筋采用HRB400.

图1 框架剪力墙平面布置图Fig.1 Frame-shear wall structural plan layout

1.2 建立2D有限元模型

将原结构剪力墙按抗侧移刚度等效为一榀总剪力墙，并均匀分配至三榀框架结构，取其一榀利用ABAQUS建立2D结构分析模型(如图2所示).考虑现浇楼板与配筋对框架梁的影响，以及减小高阶模态的干扰，保证框架结构以剪切型的第一阶模态振动.将有限元模型框架梁柱线刚度比取为10，以满足规范对刚性楼板的假定,通过保持梁截面尺寸不变，把梁的弹性模量放大,楼板质量通过附加质量源分配至梁柱节点上.

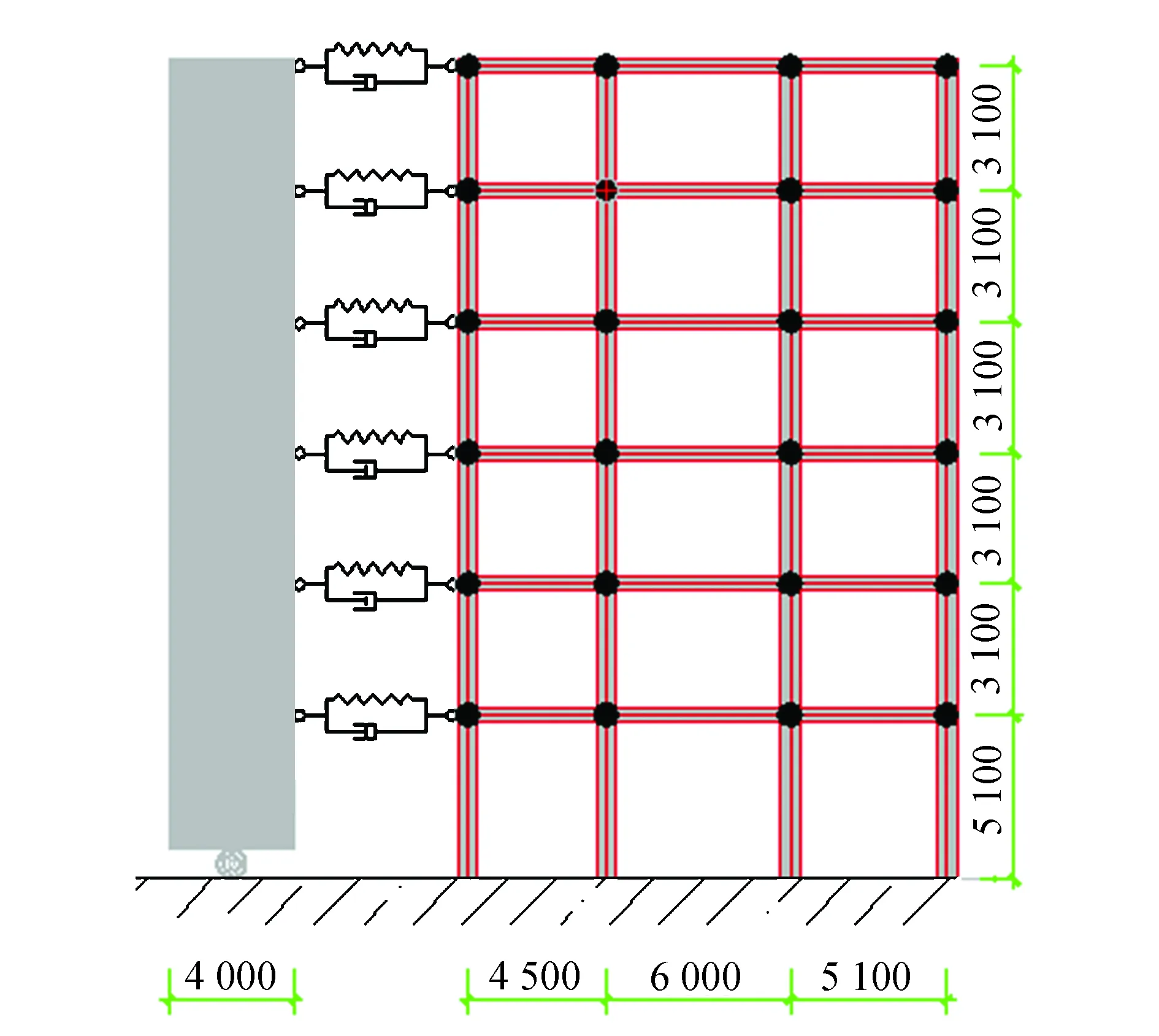
图2 结构分析模型

2 模型的基本信息与模拟

2.1 单元类型的选取

将原结构电梯井剪力墙按刚度等效为一字形，并均匀分配至三榀框架上，取其中一榀建立2D有限元模型，剪力墙厚度为250 mm，等效长度为4 m，用S4R壳单元模拟；框架柱和框架梁均采用B31纤维梁单元模拟；传统结构连梁长度为1 m，混凝土本构模型采用PQ-Fiber材料库中忽略混凝土抗拉强度的模型Uconcrete01.

2.2 BRB基本信息

对于BRB屈服强度和初始刚度的取值，考虑与原结构的可对比性，以及将来该体系抗震设计与现有规范保持一致性，将传统结构在中震(0.3g)作用下动力时程分析获取的结构总基底剪力，按倒三角沿结构高度分配至每层，将每层获得的水平剪力作为该层BRB的屈服强度值，顶层标识为fy.为了暂时减小变量，BRB屈服变形取为0.0035 m[13]，由此求出各层BRB的初始刚度，亦呈倒三角沿结构高度成比例变化，该模型称为BRB基准模型.

为分析BRB屈服强度(初始刚度)对地震响应的影响，在基准模型的基础上，变化顶层BRB屈服强度值，其他各层等比例变化，建立具有不同屈服强度(初始刚度)的BRB框架剪力墙模型(模型2)，即顶层BRB屈服强度依次为0.1fy、0.3fy、0.5fy、fy、1.5fy、2fy、2.5fy、3fy共计8个工况，屈服强度比α依次为0.1、0.3、0.5、1、1.5、2和3.

BRB本构采用如图3所示的双线性随动硬化本构.材料参数包括屈服强度fy、初始刚度K0，屈服后刚度K1取初始刚度的5%.

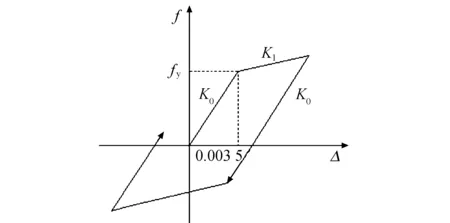
图3 基本模型中BRB本构关系Fig.3 BRB constitutive relation in the basic model

2.3 墙底金属阻尼器基本信息

金属阻尼器采用ABAQUS有限元中的非线性弹簧单元模拟.单元参数的选取考虑了混凝土剪力墙塑性铰区的抗倾覆承载能力和不同性能水准的塑性铰转动能力.

1) 剪力墙塑性铰区的抗倾覆承载力

为计算塑性铰区的抗倾覆弯矩，依据参考文献[15]确定混凝土塑性铰区的高度lp，传统结构中剪力墙的剪跨比λ=1.28<1.5，由文献[16]推荐的公式计算剪力墙塑性铰的抗剪承载力为V=1.7×106N，抗倾覆弯矩为Mu=Vlp=2.9×106N·m.

2) 非线性弹簧的初始刚度

对于剪力墙结构，FEMA356[17]给出了三个性能水平对应的剪力墙底部塑性铰转角值，取剪力墙根部塑性铰的抗倾覆弯矩Mu对应防止倒塌的塑性铰转角限值0.02 rad，屈服弯矩My对应使用良好的塑性铰转角限值0.002 rad，屈服后转动刚度与初始转动刚度比为0.05，以此推算非线性弹簧屈服弯矩为My=2×106N·m，非线性弹簧初始转动刚度为C=1×109N·m/rad.本构关系如图4所示.

图4 金属阻尼器本构关系Fig.4 Constitutive relation of metal damper

2.4 有限元模型建立

1) 传统结构(模型1)

本模型为传统框架剪力墙结构，框架与剪力墙之间通过连梁连接，为本次研究的原结构模型.

2) 设置BRB的智能框架剪力墙双重结构(模型2)

将原框架剪力墙结构的连梁替换为BRB，由BRB在地震作用下进行滞回耗能，因BRB的屈服强度和刚度不同建立了8个工况模型.

3) 摇摆墙与框架间连接BRB结构(模型3)

摇摆墙底部铰接，放松绕Z轴方向的转动约束，保证墙体在平面内的转动.框架与摇摆墙间连接BRB，通过结构墙体摇摆特性和BRB滞回耗能共同作用以达到减震耗能效果，因BRB的屈服强度和刚度不同建立了8个工况模型.

4) 双重耗能机制的智能框架摇摆墙结构(模型4)

框架与摇摆墙间连接BRB，同时在摇摆墙底部设置金属阻尼器，以实现在地震作用下的双重耗能机制，因BRB的屈服强度和刚度不同建立了8个工况模型.

2.5 地震波的选取

由于该双重耗能机制的智能框架摇摆墙结构为新型结构体系，地震动记录类型和数量的选取考虑了一定的统计特征，考虑地震动的类型、强度、持时、震中距和场地等因素，选取了6条实际地震动记录，见表1.

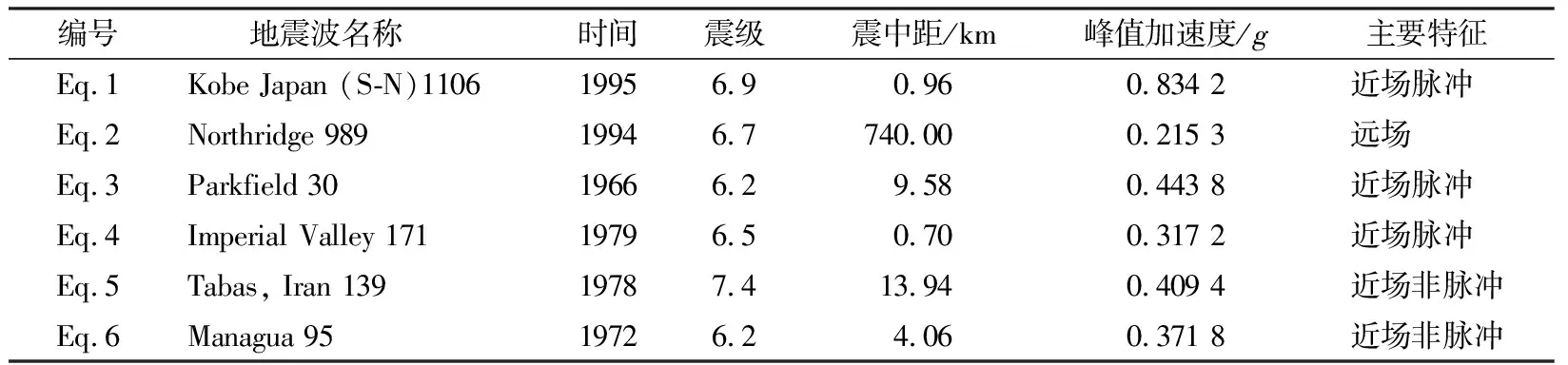
表1 地震动记录选取

3 动力分析结果

所有地震响应数据均取6条地震波的平均值.课题组已经对设置BRB的智能框架剪力墙双重结构(模型2)与传统框架剪力墙结构(模型1)进行了非线性动力时程分析与对比，结果表明：当BRB的屈服强度在0.1fy～0.3fy范围变化时，结构的地震响应参数得到了有效控制.下文将对模型3和模型4进行非线性动力时程分析，以及四个模型对比分析.

3.1 摇摆墙与框架间连接BRB结构

3.1.1最大侧向位移

1) 框架结构最大侧向位移

图5为模型3中不同BRB屈服强度结构工况与原结构的各楼层侧向最大位移比值(以下分析的响应参数均做相同处理)随BRB屈服强度变化的规律曲线.由图可知,BRB的屈服强度在0.1fy～0.5fy时，框架侧向最大位移响应均比传统结构有所减小，框架各层下降程度有所不同.随着BRB屈服强度的增大，各层位移均增加，增大到1.5fy时，侧向位移大于传统结构，当达到2.5fy时，位移变化逐渐趋于稳定.

图5 框架位移峰值随BRB变化曲线

2) 摇摆墙顶层最大侧向位移

由于摇摆墙具有较大的刚度，且底部为理想铰接，故提取摇摆墙顶层侧向位移进行分析.图6为摇摆墙顶层侧向最大位移比值随BRB屈服强度变化的曲线，变化规律和框架顶点最大侧向位移形状相似，最大侧向位移相比于传统结构所减小的范围在0.1fy～1fy之间，在0.3fy时减小了19.5%.

图6 墙顶位移峰值随BRB变化曲线 Fig.6 The variation curve of wall-top displacement peak with BRB

3.1.2框架层间位移角

在传统框架剪力墙结构中，剪力墙做为第一道抗震防线，而框架结构主要承受重力荷载作用，关系到整体结构的安全性.模型3的层间位移角与原结构比值随BRB屈服强度变化的规律如图7所示.由图可知,除首层层间位移角有所减小外，其它各层相比传统结构有所增大.但通过对比各工况的层间位移集中系数(drift concentration factor,DCF)[4]发现，传统结构DCF值为1.72，当BRB屈服强度为0.1fy～0.5fy时，DCF值为1.2左右，更接近于1，表明此时结构的层间变形趋于均匀.

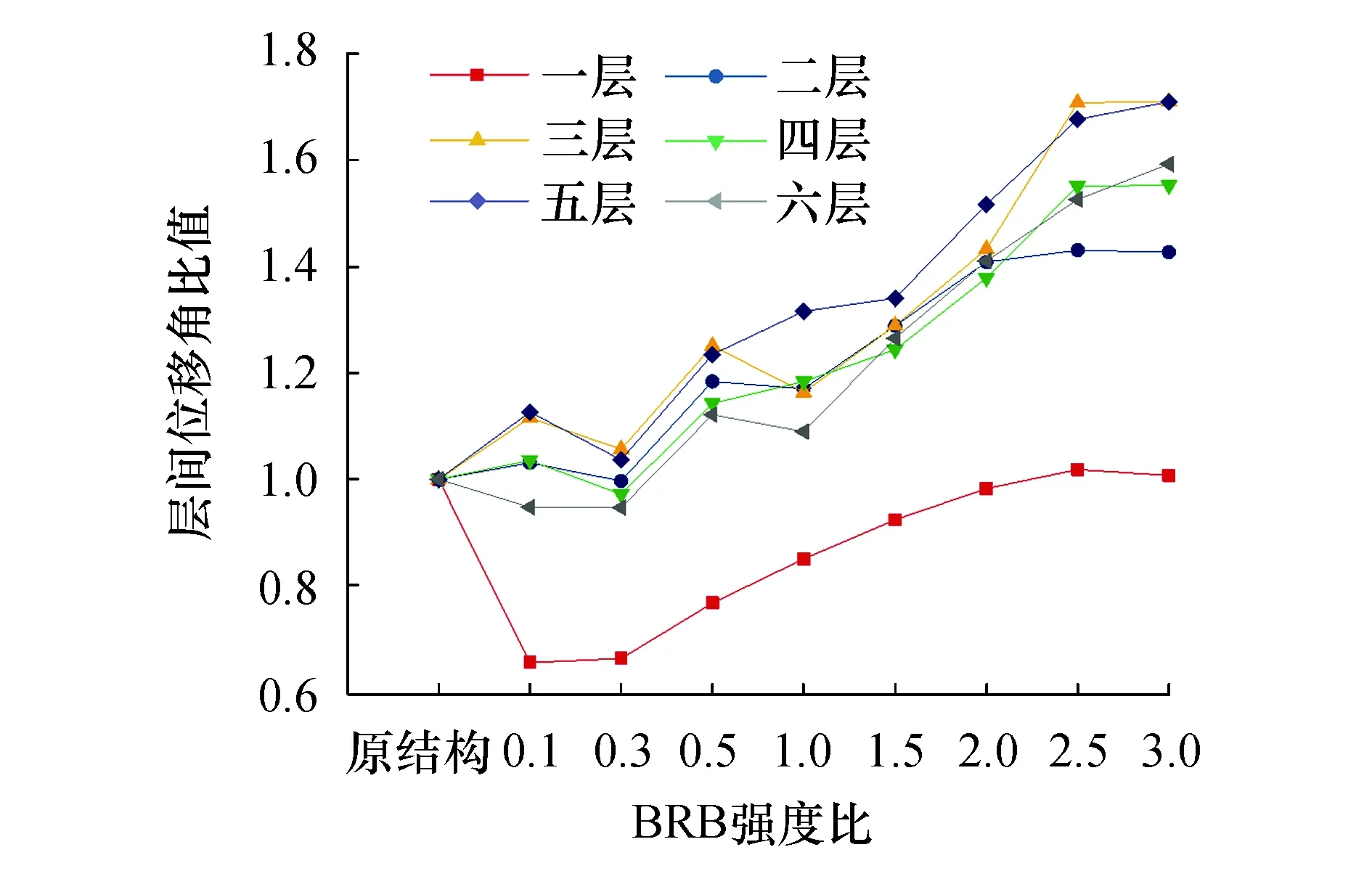
图7 层间位移角随BRB变化曲线Fig.7 The variation curve of inter-story drift with BRB

3.1.3峰值加速度

1) 框架结构峰值加速度

图8为模型3框架峰值加速度比值随BRB屈服强度变化曲线，变化趋势基本与前面的响应参数相似.由图可知，BRB的屈服强度在0.1fy～1fy时，框架结构各层峰值加速度小于传统结构，各层下降程度有所不同，最大下降了44.4%.

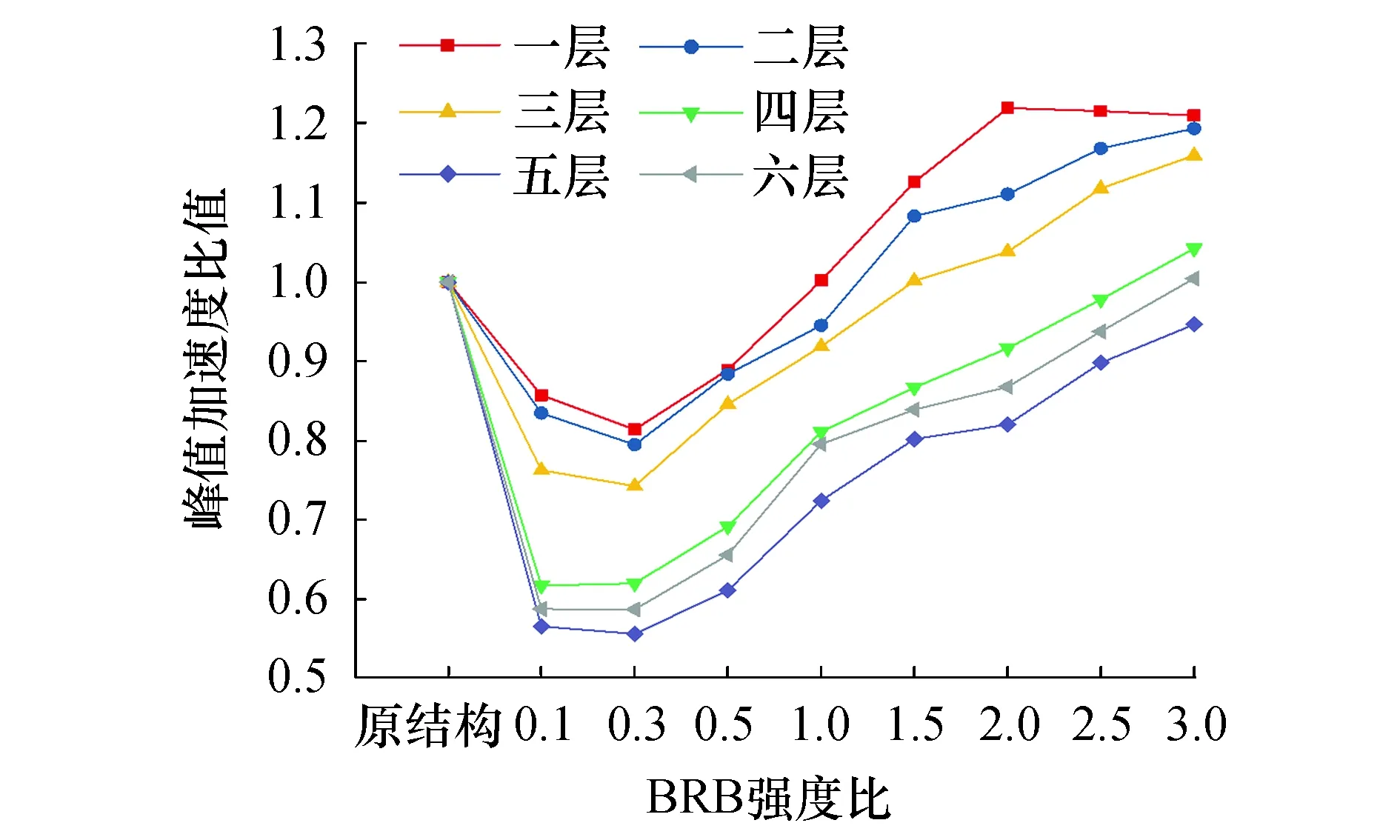
图8 框架峰值加速度随BRB变化曲线Fig.8 The variation curve of frame peak acceleration with BRB

2) 摇摆墙顶层峰值加速度

摇摆墙顶层峰值加速比值随BRB屈服强度变化如图9所示.相比于传统结构，模型3的摇摆墙顶层峰值加速度均有所减小，减小的最大幅度为42.2%.

图9 墙顶峰值加速度随BRB变化曲线

可见对于摇摆墙与框架间连接BRB的结构，合理选取BRB屈服强度和刚度参数，可以有效控制结构的水平加速度响应.

3.1.4结构基底剪力

整体结构、框架与墙体基底剪力变化曲线如图10所示.BRB的屈服强度取值在0.1fy～1fy范围时，基底剪力均比传统结构有所减小，框架柱基底剪力最大下降了22.7%.设置BRB的框架摇摆墙结构，摇摆墙基底剪力均小于传统结构，最大下降幅度达到了84.3%，充分表明BRB在结构中的“切断”机制，当BRB屈服时，阻断了主要由重力框架产生的惯性力向摇摆墙的传递.

图10 基底剪力随BRB变化曲线Fig.10 The variation curve of base shear with BRB

综上所述，框架和摇摆墙之间连接具有滞回耗能能力的BRB构件，所设置的BRB强度和刚度参数沿高度方向呈倒三角分布，当屈服强度处于0.1fy～0.5fy范围时，除层间位移值较传统结构有所增大外，框架与摇摆墙的峰值加速度、侧向位移、层间位移集中系数和基底剪力地震响应参数得到有效控制.

3.2 双重耗能机制的智能框架摇摆墙结构

模型3在控制地震响应方面虽有一定的控制效果，但层间位移有所增大.因此,在摇摆墙底部设置具有一定初始刚度和滞回耗能特性的金属阻尼器，形成双重耗能机制的智能框架摇摆墙结构(模型4)，以达到减小框架各层层间位移角的目的.

3.2.1最大侧向位移

1) 框架结构最大侧向位移

框架结构各层最大侧向位移比值如图11所示，所有分析工况中框架结构各层侧向最大位移响应均比传统结构有所减小，框架各层下降程度有所不同，BRB屈服强度为0.1fy的工况模型第一层下降幅度达49.1%，接近传统结构的一半；当BRB屈服强度达到2.5fy时，位移变化逐渐趋于稳定.

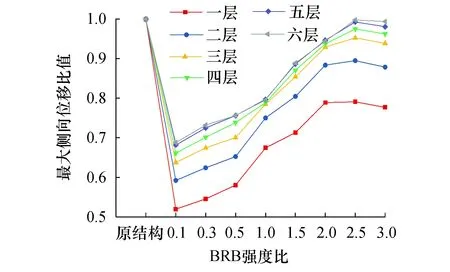
图11 框架位移峰值随BRB变化曲线 Fig.11 The variation curve of frame displacement peak with BRB

2) 摇摆墙顶层的最大侧向位移

图12为模型4墙体顶层侧向最大位移比值随BRB屈服强度变化的规律曲线，摇摆墙顶层最大侧向位移在该模型所有不同BRB参数工况中均比传统结构有所减小.表明在模型4中BRB亦具有屈服“切断”机制.

图12 墙顶位移峰值随BRB变化曲线Fig.12 The variation curve of wall-top displacement peak with BRB

3.2.2框架层间位移角

框架层间位移角比值如图13所示.BRB屈服强度在0.1fy～1fy时，框架结构各层层间位移角相比传统结构均有所下降，首层层间位移角下降最明显，最多下降了48.7%；随着BRB屈服强度的增大，各层层间位移角均增加，当达到2.5fy时，各层层间位移角变化逐渐趋于稳定.

图13 层间位移角随BRB变化曲线

3.2.3峰值加速度

1) 框架结构峰值加速度

模型4框架结构峰值加速度与模型3类似，随BRB屈服强度变化的规律曲线如图14所示.BRB的屈服强度在0.1fy～2.5fy时，框架结构各层峰值加速度响应均有所减小，最大减小幅度达到50.3%.与模型3相比，加速度峰值减小所需要的BRB屈服强度(刚度)取值范围更广.

图14 框架峰值加速度随BRB变化曲线Fig.14 The variation curve of frame peak acceleration with BRB

2) 摇摆墙顶层峰值加速度

墙体顶层峰值加速度比值随BRB屈服强度变化的规律曲线如图15所示，变化趋势与框架各层峰值加速度相同，降低的最大幅度为48.8%.

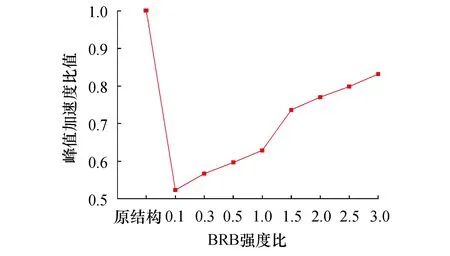
图15 墙顶峰值加速度随BRB变化曲线 Fig.15 The variation curve of wall-top peak acceleration with BRB

3.2.4结构基底剪力

图16为不同BRB屈服强度结构与原结构模型的基底剪力比值随BRB屈服强度变化的规律曲线.BRB的屈服强度在0.1fy～2fy时，模型4结构的各部分基底剪力均比传统结构有所减小，框架柱剪力最大下降了22.7%，墙底剪力最大下降了78.1%.

图16 基底剪力随BRB变化曲线Fig.16 The variation curve of base shear with BRB

综上所述，双重耗能机制的智能框架摇摆墙结构，在选定的金属耗阻尼器参数下，BRB的屈服强度在0.1fy～1fy之间时，层间位移角得到有效控制，并且小于传统结构；另一方面,侧向位移、峰值加速度和基底剪力地震响应参数小于传统结构的BRB参数,选择比模型3范围更广.

3.3 四个模型结果对比

为了明确双重耗能机制的智能框架摇摆墙结构在地震作用下响应的减小和控制的效果，将智能框架剪力墙BRB结构(模型2)、摇摆墙与框架间连接BRB结构(模型3)和双重耗能机制的智能框架摇摆墙结构(模型4)中的BRB屈服强度(刚度)取值为0.1fy，与传统结构(模型1)的地震响应进行对比.

3.3.1剪力墙/摇摆墙顶层地震响应

表2列出了四个模型剪力墙/摇摆墙顶层最大侧向位移与峰值加速度响应，设置BRB的模型相比传统模型均有所减小，充分表明BRB的屈服“切断”机制，有效抑制了重力框架产生的惯性力向抗侧力体系的传递.最大侧向位移响应排序为模型2<模型4<模型3<模型1.墙体顶层峰值加速度值依次减小.因此，对剪力墙或摇摆墙而言，BRB的屈服“切断”机制有效降低了墙体的地震响应，同时双重耗能机制(模型4)比单一耗能机制(模型2)更能降低墙体的峰值加速度响应.

表2 剪力墙/摇摆墙顶层地震响应

3.3.2框架各层最大侧向位移

四个模型的框架各层最大侧向位移变化(如图17)中，各模型位移大小排列顺序与墙体顶层位移相同，即模型2<模型4<模型3<模型1.

3.3.3框架各层层间位移角

图18显示了四个模型框架各层层间位移角的变化与弹性层间位移角限值的关系.由图可知,模型2、模型3和模型4的各层层间位移角变化比模型1更均匀，尤其模型2与模型4表现良好，层间位移角小于弹性限值，但模型4曲线光滑、陡直，更加优于模型2.

3.3.4框架各层峰值加速度

框架具有较大的质量，故产生较大的惯性力，为减小结构的峰值加速度和结构内力响应，允许部分结构构件进入到塑性阶段.图19为四个模型的框架各层峰值加速度曲线图，结果表明：模型2、模型3和模型4的各层峰值加速度均比模型1有所减小，模型4由于BRB与金属耗能器共同作用，减震效果最为明显.对比模型2的峰值加速度，模型3中摇摆机理对于框架的峰值加速度效果并不明显，模型3引起的不均匀性，与BRB刚度沿结构高度分布方式有关.

3.3.5最大基底剪力分析

整体结构的内力响应，一定程度上可以由基底剪力来反映.四个模型的整体结构总基底剪力、剪力墙/摇摆墙和框架结构基底剪力变化如图20所示.模型2、模型3与模型4对比传统结构模型1均有所下降.相比模型1，模型2的墙底剪力和总剪力分别下降了44.9%、30.1%.对于重力框架结构的基底剪力,模型2与模型4降低的程度比模型3更为理想，模型2在框架结构基底剪力减小方面最为明显，说明剪力墙基底固结，使得分配到了相对较大的基底剪力，从而有效减小了框架结构的基底剪力.模型3和模型4的各部分基底剪力变化不大，表明金属阻尼器对于基底剪力减小而言，效果并不明显.

综上所述，相对于剪力墙/摇摆墙而言，在框架与墙体之间连接BRB耗能单元，表现出明显的屈服“切断”机制，剪力墙结构地震响应比传统结构有所减小，同时剪力墙底部可摇摆对与剪力墙而言明显地降低了峰值加速度效应.相对于重力框架结构而言，模型2与模型4表现出了良好的抗震性能，尤其模型4不但控制了结构的位移响应，而且明显改善了框架各层峰值加速的响应.可见双重耗能单元体系比单一耗能单元体系对于减小地震响应更加有效，结构变形更加趋于均匀.