大型风力机叶片阻尼层厚度分析与抑颤研究

杨 瑞, 杨 伟, 陈志龙

(兰州理工大学 能源与动力工程学院, 甘肃 兰州 730050)

随着风力机的大型化叶片趋于长展化、柔细化,叶片自身刚度相对降低,在外界激励作用下,叶片容易发生振动.由于所受气动力和振动作用之间互相加强,叶片运动不稳定,从而发生颤振[1].叶片颤振引发的交变应力会使叶片产生疲劳裂纹甚至断裂.

为了抑制颤振,阻尼材料叶片应运而生.徐超等[2]基于Layerwise理论推导了一种层合板单元,分析共固化粘弹材料结构的阻尼性能.赵树萍等[3]推导了结构损耗因子表达式,发现约束阻尼结构可显著提高抑颤能力.韩斌慧等[4]通过对比自由阻尼层结构和约束阻尼结构,发现约束阻尼结构具有更好的减振作用.Song等[5]通过主动调节刚度和固有频率发现能将振动幅值降低.张洪宁等[6]发现多层约束阻尼叶片比普通叶片具有更高的结构阻尼.孙大刚等[7]发现在额定风速下,阻尼叶片比普通叶片摆振位移和挥舞位移的标准差分别减小了48.1%和34.8%.国外研究表明阻尼抑颤技术在保证复合材料结构刚度和强度的前提下,可显著提高结构阻尼[8].Robinson等[9]通过实验分析发现:阻尼层面积占比为95%的结构与无阻尼层结构相比,结构阻尼提高了2.2倍;当阻尼层面积占比在99.7%时,结构阻尼比前者增加了143倍.目前国内外阻尼抑颤研究主要是通过在叶片中大量增加阻尼材料提高结构阻尼来实现抑颤效果,而对阻尼材料敷设位置、敷设厚度研究很少,对大型风力机阻尼叶片抑颤效果研究更少.本文通过铺层设计、阻尼层位置设计、阻尼材料选取，建立8 MW大型风力机阻尼叶片,分析了阻尼层厚度对结构频率、结构损耗因子、叶片质量的影响,并确定了8 MW叶片阻尼层最佳敷设厚度,探究了8 MW阻尼叶片的抑颤效果,为未来大型风力机阻尼抑颤叶片的研究提供了参考.

1 风力机叶片有限元建模及铺层设计

1.1 风力机叶片有限元建模

通过设置材料属性、单元属性以及网格控制,利用ANSYS APDL命令流建立8 MW风力机叶片结构模型.叶片所用材料为复合材料GFRP,单元类型为4节点SHELL181单元,经网格控制生成有限元模型如图1所示.

图1 8 MW风力机叶片有限元模型Fig.1 8 MW wind turbine blade finite element model

1.2 铺层设计

由于本文需要建立约束阻尼结构模型,为增加结构稳定性,叶片铺层采用上下对称方式进行铺设,参考李仁年等[10]关于大型风力机叶片铺层及模态分析进行铺层设计.叶根、前缘、主梁帽、后缘铺层均采用玻璃纤维复合材料GFRP,腹板为GFRP和Balsa木两种材料.由于叶片各处所受载荷不同,从叶根至叶尖铺层层数和厚度均不相同[11],整体上从叶根至叶尖,铺层厚度逐渐减小,如图2所示.本文铺层采用全交替对称铺设,铺设方式如表1所列.表中下标“s”表示对称铺层,“t”表示已列出全部铺层,“2t”表示连续铺层,即[±45/0/90/0/±45/0/90/0]s=[45/-45/0/90/0/45/-45/0/90/0/0/90/0/-45/45/0/90/0/-45/45]、[±45/0/90/0/±45/0/90/0]2t=[45/45/0/90/0/45/-45/0/90/0/45/-45/0/90/0/45/-45/0/90/0].

表1 叶片铺层设计方案

对铺层后的叶片作模态分析,观察固有频率是否在叶片共振频率范围内,以验证铺层设计合理性.根据此次设计的转速为4.8～12.1 r/min的8 MW风力机叶片,可求得叶片发生共振时的频率为0.08～0.201 66 Hz.按本文设计的铺层方式铺层后的叶片第一阶固有频率为0.325 305 Hz,明显高于发生共振时的最大频率,因此叶片正常工作时不会发生共振.

2 阻尼叶片建模及模态分析

2.1 材料选择

叶片材料选择为玻璃纤维增强树脂复合材料GFRP,阻尼层材料选择为粘弹性阻尼材料ZN-33橡胶,ZN系列橡胶具有优良的抗疲劳性能、耐腐蚀性能以及材料损耗因子[12].GFRP和ZN-33均为各向异性材料,实际建模时要设置x、y、z各方向材料参数,具体参数如表2所列.

表2 材料力学性能参数

2.2 阻尼层铺设位置的确定

通过无阻尼结构叶片模态分析得到一阶矢量位移图,如图3所示.发现其振型主要以挥舞为主,而在沿叶片展向70%～100%处矢量相对位移较大,为提高能量耗散率,选定在该区域铺设阻尼层.

图3 无阻尼结构叶片一阶矢量位移图Fig.3 First-order vector displacement diagram of blade without damping structure

2.3 阻尼结构叶片建模

由于大型风力机叶片内部为壳体结构,考虑到计算效率、准确性、节点偏置及阻尼层的剪切变形,本文采用混合单元法对阻尼结构叶片进行建模,如图4所示.阻尼层选用8节点体单元SOLID185模拟其剪切变形,上下蒙皮选用壳单元SHELL181,中间为阻尼层,铺层方式为全交替对称铺设,划分网格后,必须用MPC接触算法在阻尼层及其上下表面创建接触,以实现接触面间的位移协调.

图4 阻尼结构叶片单元模型Fig.4 Blade unit model of damping structure

2.4 结构损耗因子

结构损耗因子η是复合结构分析的重要参数,代表了复合结构对振动能的耗散能力,结构损耗因子η越大,耗散能力越强,抑颤效果越好.有多种结构损耗因子的求解方法,最常见的方法有复特征值法、直接频率响应法、模态应变能法三种.由于本文计算基于模态分析,为避免计算大量的复特征值,所以选用模态应变能法[13].模态应变能法首先要经过有限元模态分析确定有限元模型的应变能：

(1)

用模态应变能法计算时,仅需要把阻尼材料视为具有实刚度模量的纯弹性体.可在ANSYS POST1后处理中利用ETABLE SENE命令求得应变能.

2.5 阻尼叶片模态分析

2.5.1模态分析方程

由弹性力学有限元法得到振动系统在笛卡儿坐标系中的运动微分方程：

Mγ(t)+Cv(t)+Ku(t)=F(t)

(2)

式中：M、C、K为质量矩阵、阻尼矩阵和刚度矩阵；γ(t)、v(t)、u(t)为结构加速度向量、速度向量和位移向量；F(t)为结构的激振力向量.

由于本文模型采用静态模态分析,故F(t)=0,方程此时转化为自由振动方程：

Mγ(t)+Ku(t)=0

(3)

任何弹性体的自由振动可分解为一系列简谐振动的叠加,设式(2)有简谐振动解,则

U(t)=U0sinωt

(4)

将式(3)带入式(2)可得齐次方程：

(K-ω2M)U0=0

(5)

式(4)为典型的实特征值问题,U0有非零解的条件是其系数行列式为零,即

(K-ω2M)=0

(6)

令ω2=λ,则上述行列式为λ的多项式,有根λ1、λ2、λ3、…、λn.代入λi得方程：

(K-λiM)Ui=0

(7)

式中：i=1,2,3,…，n.

因此可求得模态Ui,固有频率fi=ωi/2π.

2.5.2模态参数分析

阻尼结构模型建立后,设置约束载荷为叶片根部全约束,模态设置为六阶.对不同阻尼层厚度的阻尼叶片进行计算,分析阻尼层厚度变化对频率、最大相对位移、结构损耗因子以及质量等结构参数的影响,如表3所列.

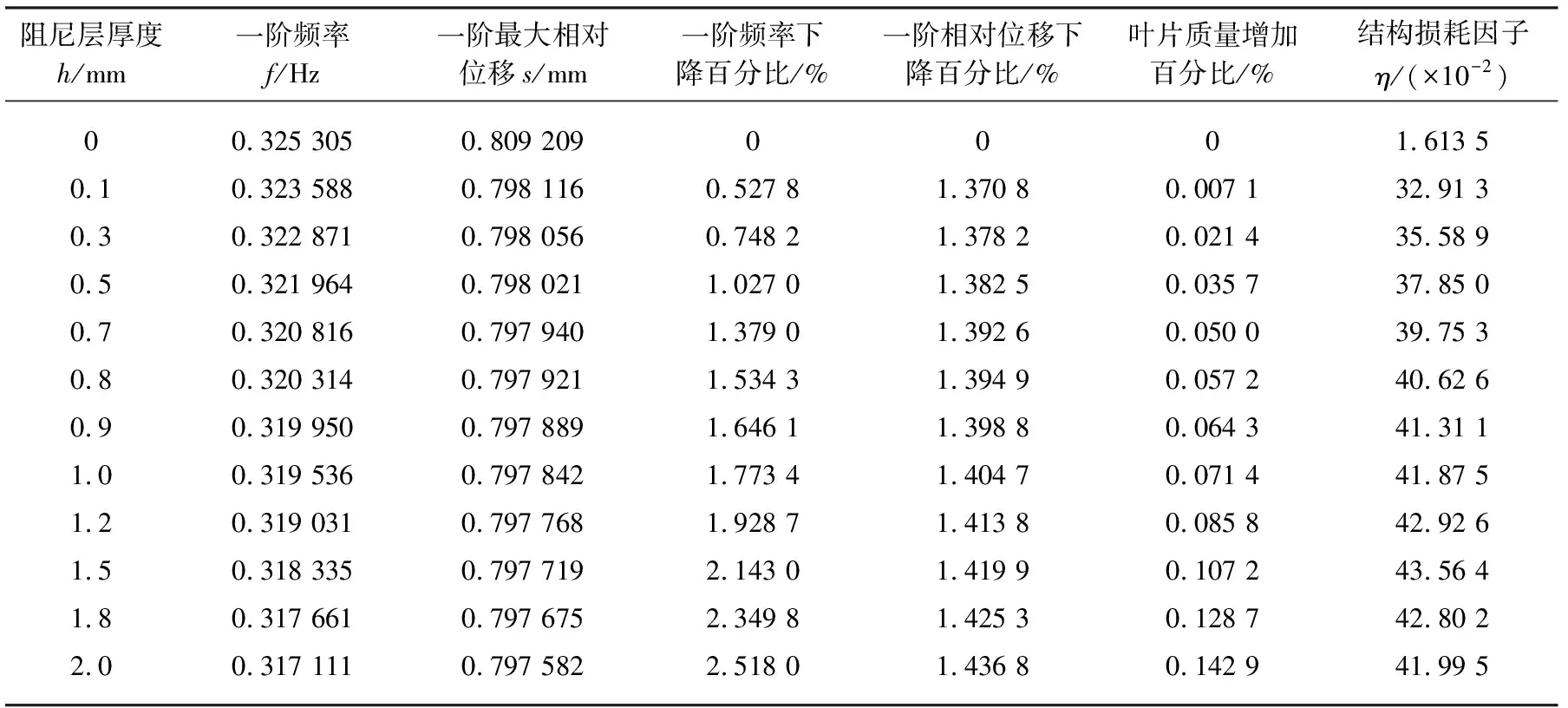
表3 阻尼叶片阻尼层厚度影响参数

1) 阻尼层厚度对叶片固有频率的影响

由表3和图5可知：当阻尼层厚度较薄、小于0.7 mm时,阻尼叶片一阶固有频率与无阻尼叶片相比略有降低；当阻尼层厚度大于0.7 mm时,频率降低幅度相对于薄阻尼层厚度有所增大.这是由于阻尼材料ZN-33橡胶弹性模量远低于叶片材料弹性模量,当阻尼层和上下蒙皮固结到一起时,拉低了整个结构的刚度,从而降低了固有频率.

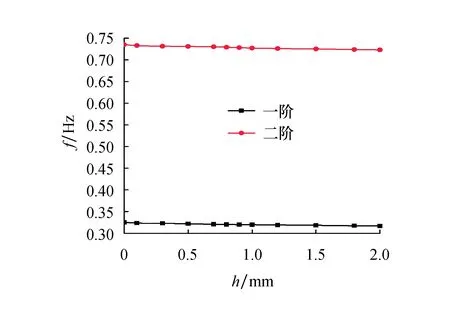
图5 固有频率随阻尼层厚度变化曲线Fig.5 Natural frequency variation curve with damping layer thickness

2) 阻尼层厚度对结构损耗因子的影响

随着阻尼层厚度增加,结构损耗因子明显增大,一阶最大相对位移也表现出明显降低趋势.这是因为当叶片受到挥舞、弯曲等变形时,阻尼层内部分子链间相互摩擦、剪切,增强了叶片对振动能的耗散作用,致使抑颤效果变优.由图6可以看出:阻尼层厚度越接近1.5 mm损耗因子增长率越小;阻尼层厚度为1.5 mm时损耗因子达到最大值,此时抑颤能

图6 结构损耗因子随阻尼层厚度变化曲线Fig.6 Curve of structural loss factor with thickness of damping layer

力最强;阻尼层厚度超过1.5 mm损耗因子开始下降.因为阻尼材料模量较小,当厚度增大到一定值时，在外力作用下阻尼层的剪切变形减小,所以阻尼层应变能表现为先增大后减小.

3) 阻尼层厚度对叶片质量的影响及最佳阻尼层厚度

目前国内已有的1.5 MW风力机单叶片质量4.5 t,全球领先的风机企业Vestas推出9.5 MW风力机叶片长度80 m、单叶片质量29 t,据此判断本文设计的8 MW风力机叶片长78.5 m、单叶片质量24.79 t符合质量范围.随着阻尼层厚度增加,叶片质量增加,当阻尼层厚度为1.5 mm时,叶片质量增加26.5748 kg,相对原叶片质量24.79 t无明显影响.为减轻塔架压力和防止出现更严重的叶片气弹不稳定问题,叶片质量不能增加过多,考虑到质量增加和结构损耗因子等因素,阻尼层厚度不宜过厚,本文阻尼叶片选择阻尼层厚度为1.5 mm,可以在少量增加质量的情况下保证抑颤效果.

3 两种叶片抑颤效果分析

3.1 两种结构叶片模态分析

由表3可知,对原叶片与阻尼层厚度1.5 mm的阻尼叶片在相同条件下进行模态分析,发现阻尼叶片一阶最大相对位移比原叶片下降1.4199%,结构损耗因子相比原叶片增大26.99倍,阻尼叶片对振动能的耗散能力远大于原叶片,说明阻尼叶片抑颤能力明显优于原叶片.

3.2 两种结构叶片静力学分析

3.2.1网格无关性验证

网格的疏密对计算结果、计算周期、计算效率产生了重要影响,因此必须找到一套合适的网格密度.本文将利用以下三套网格进行网格无关性验证：旋转域网格数1 608万,外部流场网格约1 319万,总网格数3 395万；旋转域网格数1 791万,外部流场网格约1 378万,总网格数3 536万；旋转域网格数1 820万,外部流场网格约1 446万,总网格数3 720万.用三套网格数模型进行计算,并对计算结果进行比较,发现前两套网格风轮输出扭矩最大相差约10.7%,后两套网格风轮输出扭矩最大相差3.06%.考虑到计算资源与收敛速度,选择第二套网格.

3.2.2静力学分析

通过设置额定风速和额定转速,根据原叶片内外域流场模拟气流流场,在FLUENT中计算叶片功率,直到计算结果接近理论额定功率,再由数值模拟结果导出叶片表面压力载荷,所得载荷为额定风速下载荷.具体操作如下：首先在APDL模块叶片表面建立表面效应单元SURF154,进行网格划分后利用Write操作导出表面效应单元数据到FLUENT;然后在FLUENT模块中读取压力载荷;最后再利用read操作将载荷数据读入到有限元模型,得到原叶片表面压力载荷,同理得到阻尼叶片表面压力载荷.施加根部约束后对两种有限元模型进行计算得到x、y、z三个方向总的位移变化,并选定沿叶片展向10%、25%、50%、80%、100%处五个点的位移进行分析.图7a和图7b分别为无阻尼和阻尼叶片压力载荷图.

图7 两种叶片静压力位移对比Fig.7 Comparison of static pressure displacement of two blades

由图7可知,阻尼叶片与无阻尼叶片最大压力载荷相同,这是因为阻尼层在蒙皮中间,阻尼叶片表面效应单元与无阻尼叶片表面效应单元相同,所以读入的压力载荷也相同.在压力载荷作用下计算可知阻尼叶片在展向10%、25%、50%、80%、100%处五个点的总位移分别降低了2.09%、3.85%、5.45%、5.42%、5.47%,说明叶片经敷设阻尼层后总位移波动幅度明显下降,靠近叶根处降幅小,靠近叶尖处降幅大.另外通过对比50%、80%、100%处三个点在x、y、z三个方向位移幅值,发现y向挥舞位移下降最多,x向摆振位移次之,z向降幅最小.这是因为挥舞方向位移波动幅度大,模态损耗因子更高,对振动能的耗散率更高,所以挥舞方向抑颤效果更好.其中叶展100%处x、y、z三个方向位移幅值分别下降了4.292%、6.368%、3.317%.综上所述,施加压力载荷后,阻尼叶片抑颤效果明显优于无阻尼叶片,x、y、z各方向位移参数如表4所列.

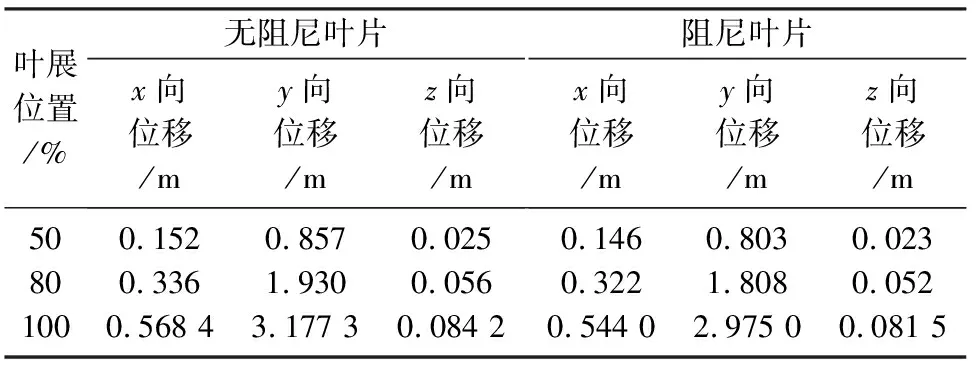
表4 x、y、z各方向位移变化

3.3 两种结构叶片瞬态动力学分析

3.3.1瞬态动力学基本方程

瞬态动力学基本运动方程为

(8)

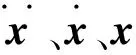
其中,阻尼矩阵一般由粘性阻尼矩阵和结构阻尼矩阵求出[14]：

C=Cv+Cs=αM+βK

(9)

式中：Cv为黏性阻尼矩阵；Cs为结构阻尼矩阵;α、β是不依赖于频率的常数,由实验测出.

3.3.2瞬态计算

瞬态分析可直观地反映出随机风载作用下两种结构叶片随时间的变化情况.本文瞬态分析规定方法采用Full完全法,随机风载采用表格方式加载.由于风力机叶片所受载荷以气动载荷为主,而气动载荷往往具有随机性,为了能准确计算风机叶片上的随机风载,使其更接近工程实际,本文将采用双参数威布尔分布函数模型拟合随机风速曲线[15],结合伯努利方程可求得对应风速下的风载,计算公式如下：

(10)

式中:WP为动态风压,N/m2；ρ为空气密度,kg/m3；v为随机风速,m/s.标准状态下ρ=1.25,可得:

Wp=0.625v2

(11)

设置步数为400步,结束时间为30 s,时间步长为0.02 s,经计算得阻尼系数α为0.23,β为0.013 5.对两种结构叶片在同一条件下叶尖处的挥舞和摆振位移进行对比,所得结果如图8所示.

由图8可知:在随机风载作用下,无阻尼叶片y向挥舞位移最大幅值为2.234 15 m,x向摆振位移最大幅值为0.196 92 m;阻尼叶片y向挥舞位移最大幅值为1.762 m,x向摆振位移最大幅值为0.163 195 m.阻尼叶片相比原叶片挥舞位移最大值下降了21.133%,摆振位移最大值下降了20.665%.同时,阻尼叶片挥舞和摆振方向位移基本上同时在20 s时趋于稳态,相比原叶片提前趋于稳态.结合位移幅值变化和趋于稳态时间,发现设计的阻尼叶片相比原叶片抑颤效果有明显提升,且对挥舞方向的抑颤效果略高于摆振方向.

图8 两种叶片不同方向位移曲线对比Fig.8 Comparison of displacement curves of two blades in different directions

4 结论

1) 通过对比固有频率、结构损耗因子等结构参数分析了阻尼层厚度对叶片抑颤性能、结构刚度的影响,叶片质量随阻尼层厚度的变化情况,最终确定了8 MW风力机阻尼叶片阻尼层最佳厚度为1.5 mm,并建立了阻尼叶片.

2) 通过模态分析、静力学分析和瞬态动力学分析分别讨论了阻尼叶片与无阻尼叶片最大相对位移和结构损耗因子变化情况,沿叶展10%、25%、50%、80%、100%处五个点两种叶片位移变化情况,x、y、z三个方向各点变化情况以及挥舞位移、摆振位移波动幅度及趋于稳态时间.发现阻尼叶片结构损耗因子是无阻尼叶片的26.99倍,阻尼叶片五处位置总位移分别下降了2.09%、3.85%、5.45%、5.42%、5.47%,挥舞位移和摆振位移最大值分别下降了21.133%、20.665%,相比原叶片阻尼叶片提前趋于稳态,挥舞方向抑颤效果最好.

3) 阻尼叶片抑颤性能相比无阻尼叶片有明显提升.大型风力机叶片在合理敷设阻尼层厚度的条件下,通过少量增加质量就能提高抑颤效果.