基于改进果蝇优化算法的随机森林回归模型及其在风速预测中的应用
2021-09-03朱昶胜李岁寒
朱昶胜, 李岁寒
(兰州理工大学 计算机与通信学院, 甘肃 兰州 730050)
风速的波动性和随机性导致风电机组输出功率的不确定性,这使得风电并网对电力系统的稳定运行产生严重影响[1].对风速作出比较准确的预测可以及时进行电网调度,从而提高风力发电的质量[2].因此如何实现风速的准确预测一直是研究的热点.目前风速预测的方法主要有支持向量机(support vector machine,SVM)[3]、最小二乘支持向量机(least square support vector machine,LSSVM)[4]和人工神经网络[5]等,但这些预测模型都存在着自身局限性.SVM、LSSVM能解决非线性、小样本等实际问题,但泛化能力不强,且其关键参数不易确定[6].人工神经网络模型具有较好的自学能力,但存在收敛速度慢、易陷入局部最优的问题,同时其网络结构难以确定[7].随机森林回归(random forest regression,RFR)[8]是随机森林(random forest,RF)的主要应用类型,目前已广泛用于解决回归问题.与人工神经网络相比,RFR具有较高的稳定性,且不易过拟合.与SVM相比,RFR具有更高的拟合精度,对数据中噪声和离群点的耐受性更好.模型参数的选择往往对预测结果有着重要影响,通常RFR中参数选择采用经验值,但取值结果不理想,因此对参数的优化是提高预测精度的有效方法.
李国等[9]采用提升回归树和RF的集成算法对风电功率进行预测,实现了更为准确的风电功率预测,但模型参数选择采用经验值,难以得到全局最优解.方馨蕊等[10]将RFR模型应用于悬浮泥沙浓度预测,结果表明RFR模型预测值与实际值相关性好、预测精度高,不过在模型构建中通过遍历参数组合来选择最优参数需要大量训练时间.Sun等[11]结合RF和深度置信网络对风速和风功率进行预测,实验表明与现有方法相比,所提方法在预测精度和扩展性方面具有优势,然而RF构建中使用K折交叉验证调优,计算量大、实验成本高.赵东等[12]使用果蝇算法优化RF参数,研究表明优化后的模型进行问题预测具有更精准的结果,但果蝇优化算法搜索步长固定,局部探索能力差.
针对上述问题,本文从预测模型参数优化方面入手以提高预测精度,提出了一种基于改进果蝇优化算法(improved fruit fly optimization algorithm,IFOA)的RFR风速预测模型.改进果蝇算法搜索步长使其在迭代过程中自适应更新,定性分析生成树数目(ntree)和树的最大深度(mdepth)对RFR模型性能的影响,并利用IFOA算法进行参数寻优,对比多种群果蝇优化算法(multi-swarm fruit fly optimization algorithm,MFOA)[13]、果蝇优化算法(fruit fly optimization algorithm,FOA)、粒子群优化算法(particle swarm optimization,PSO)和IFOA在RFR参数优化中的结果,验证了改进算法在全局搜索和寻优效率上的优越性.构建了IFOA-RFR风速预测模型,并与MFOA-RFR、FOA-RFR、PSO-RFR、RFR、SVM进行预测结果对比,结果表明IFOA-RFR模型具有更小的预测误差和更好的拟合度.
1 IFOA-RFR算法
1.1 随机森林回归
RFR是由Breiman提出的以回归树[14]为基学习器的集成学习模型,该算法调节参数少,对噪声和异常值具有良好的容忍度并且可有效避免过拟合,常可获得比单个回归树更显著的泛化性能和准确性.该算法利用自助聚集策略[15]从原始数据中提取多个样本,为每个样本构建一个子树,结合所有子树的预测结果得到最终结果,因此常可获得比单个回归树更显著的泛化性和准确性.其基本原理是通过回归之间的互补原则将多个弱回归树组合成一个强回归树以提高全局准确性,所以该模型有较强的鲁棒性.算法回归预测的基本流程为:
1) 从训练集L中按照随机的、有放回的、重新选择的方式产生P个相互独立的样本子集Li:
其中:N表示训练集数据的数量;NB代表样本子集数量.
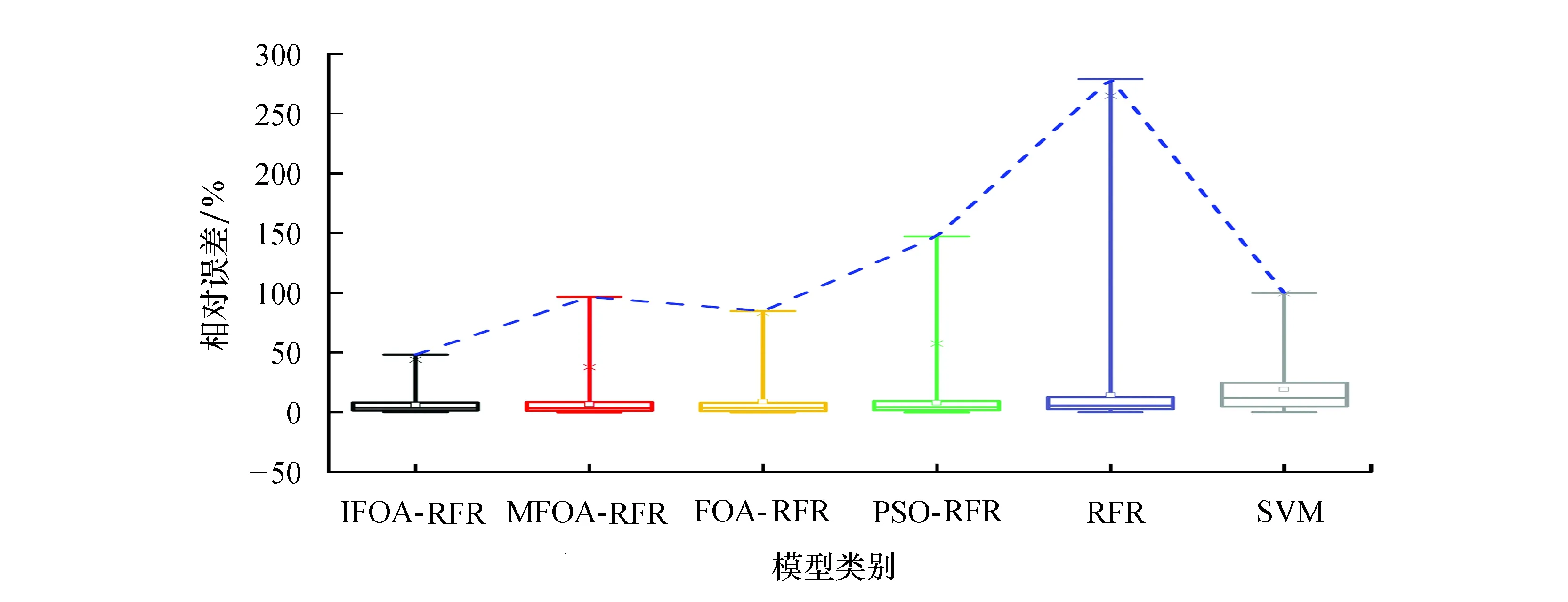
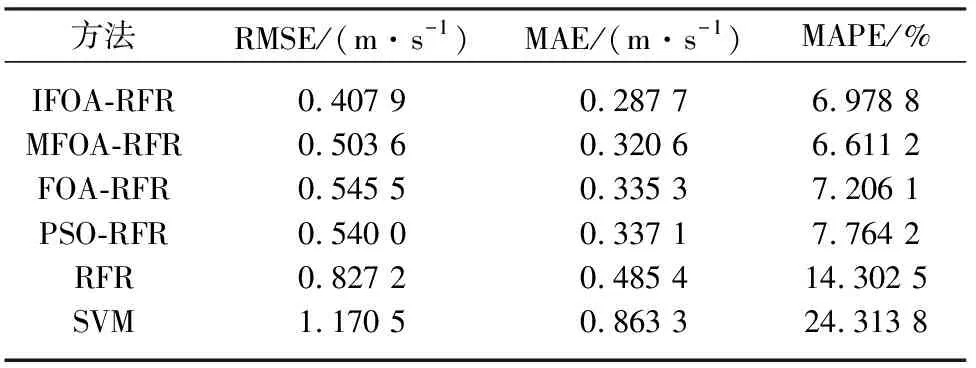
2) 任意样本子集Li中,NB(NB (3) RFR模型中生成树数目(ntree)、树的最大深度(mdepth)和候选分裂属性数(mtry)会影响模型性能[18],其中:ntree代表建立子树的数量,当子树的数量增加时模型的稳定性和预测精度更好,但是当ntree数量值达到某个阈值后再增加该值不会提高模型准确性,反而会导致模型效率降低;mdepth为树的最大生长深度,更高的深度将有利于学习样本的特定关系;mtry表示子树选取特征的最大数量,影响着模型的随机性[19-20].由于本实验中风速数据集样本特征量较少,因此mtry的值设为None,即选取所有特征对每棵树不加限制.RFR中参数ntree与mdepth的选择会对预测结果产生影响,因此通过IFOA对参数ntree与mdepth进行迭代寻优的方式来获取最佳参数值,将IFOA和RFR的结合定义为IFOA-RFR. FOA算法是将果蝇的觅食行为归纳为随机搜索和视觉定位过程而提出的一种新型群智能优化算法[16].FOA算法基于实数编码,且与PSO、遗传算法(genetic algorithm,GA)等群智能优化算法相比,具有收敛速度快、易于理解和设置参数少的优点.FOA的迭代过程如图1所示. 图1 FOA迭代过程Fig.1 The iterative procedure of FOA FOA算法的具体步骤如下: 1) 初始化.将种群大小定义为Popsize,并将种群的初始位置定义为(X,Y). 2) 随机搜索.赋予果蝇随机飞行的方向和步长: X(i)=X+R (4) 其中:(X(i),Y(i))是第i个果蝇的位置,i=1,2,…,Popsize;R表示步长值. 3) 味道浓度判定值S(i)的计算: (5) 4) 味道浓度值的计算.根据味道浓度判定值获得味道浓度值: Smelli=F(S(i)) (6) 其中:Smelli表示第i个果蝇个体的味道浓度值;F表示适应度函数. 5) 寻找具有最佳味道的果蝇个体: Smellbest=max{Smell} (7) 其中:Smellbest代表在果蝇群体中具有最佳味道浓度值的个体. 6) 假设当前最佳位置的果蝇个体位于(Xbest,Ybest),其气味浓度值为Smellbest,然后果蝇群向该处飞去: (8) 7) 重复步骤(2~5),然后确定当前的最佳味道浓度是否优于先前的最佳值.如果是,执行步骤6).算法在满足预设条件后停止. 由于FOA算法搜索步长固定,导致其收敛效率低且易陷入局部最优[17].为解决此问题,采用三角函数和指数函数改进FOA算法中果蝇飞行的随机方向和飞行半径,将改进后的算法称为IFOA. 在IFOA算法中,指数函数机制使步长变化具有非均匀性,从而更容易捕捉到最优值,有利于全局搜索;三角函数机制使步长的变化尺度更具随机性,避免算法陷入局部最优.步长改进如下: (9) 其中:j为当前迭代次数;i为当前果蝇个体;(Xj,Yj)为果蝇当前迭代中的最佳个体位置;randValue为随机变量;(X(i)j,Y(i)j)为第j次迭代中果蝇个体i的位置;Rj为第j次迭代的搜索步长;P为指数因子;自变量c随着迭代次数的增加而增加;Maxtimes为算法迭代次数的最大值;ω为权重因子;λ为常量. IFOA继承了FOA收敛速度较快的优点,同时采用自适应步长使果蝇在合理且不断变化的搜索范围内快速寻找到最优解,不仅提高了FOA算法在较大范围内的全局搜索能力,同时增强了该算法的局部觅食能力. 基于IFOA-RFR的风速预测分为内部参数优化和外部预测性能评估两部分.在内部参数优化部分,通过IFOA算法优化RFR模型的ntree和mdepth参数,IFOA算法依旧采用FOA算法的实数编码方式;在外部预测性能评估部分,使用优化后的RFR模型进行风速预测,并作误差分析以评估模型性能.图2是IFOA-RFR模型的具体流程,步骤如下: 图2 IFOA-RFR流程Fig.2 IFOA-RFR process 1) 数据输入与模型构建.划分历史风速数据为训练数据集和测试数据集.设定RFR模型中参数ntree和mdepth为变量n和m,从训练数据集中利用Bootstrap方法抽取样本进行模型训练并用测试数据集进行预测. 2) 定义适应度函数F(n,m).将实际风速值和通过RFR模型得到的预测风速值的均方根误差(root mean square error,RMSE)作为适应度函数的返回值,适应度值越小则代表模型预测效果越好. 3) 初始化.初始化果蝇群体起点位置(X,Y),给定种群大小Popsize、最大迭代次数Maxtimes和初始果蝇个体飞行半径R. 4) 果蝇个体随机搜寻食物: (10) 由于对n和m两个参数进行寻优,因此X与Y各有两列数值.且第j次迭代后迭代步长为Rj,当j=0时,R0=R.第i个果蝇个体的位置为(X(i,1),Y(i,1)),(X(i,2),Y(i,2)). 5) 计算果蝇与原点的距离值D并求得味道浓度判定值S: 对n和m进行赋值: 将n和m代入RFR模型计算适应度函数F(n,m),并对果蝇个体的味道浓度Smelli进行赋值: Smelli=F(n,m) (15) 求果蝇群体中味道浓度最佳值,味道浓度最佳值即适应度的最小值,因此索引味道浓度的最小值: (16) 6) 保留最佳味道浓度值Smellbest并记录相应坐标,果蝇群利用视觉朝该位置飞去: (17) 7) 更新迭代步长: Rj+1=Rj×pc×ω (18) 8) 迭代优化.如果当前迭代次数j 9) 输出结果: 利用参数优化后的RFR模型进行风速预测并进行误差分析. 以山西某风电场2015年5月的1 152组采样间隔为15 min的风速数据作为研究样本,取前960组数据作为训练集,后192组数据作为测试集.实验数据走势和划分如图3所示,Train set部分代表训练集,训练集共960组数据,Test set部分代表测试集,测试集共192组数据.风速数据分布如图4所示.由图4可以看出,数据分布具有集中性且数值在正态分布曲线高峰处向两侧不均匀下降. 图3 每15 min的风速序列Fig.3 Sample data for every 15 minutes 采用最值归一化(min-max normalization,MMN)方法进行数据的无量纲处理,将数据值映射至[0,1]区间,预测完成后通过反归一化将预测值转化到原区间. 实验选择RMSE、平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差MAPE(mean absolute percentage error,MAPE)以及相对误差(relative error)作为预测结果的评价指标: (21) 1) RFR优化参数分析 为进一步定性说明参数ntree与mdepth对模型精度的影响,将采集得到的风速数据前960组作为训练集,后192组作为测试集,当ntree∈[1,10],mdepth∈[1,50]且step=1时,其模型风速预测值与实际值的RMSE变化曲线如图5所示.在图5中n代表ntree,m代表mdepth. 从图5可以观察到,不同的n与m组合影响着RMSE的变化,RMSE取值不同则映射区域不同.若m固定不变,随着n值增加,RMSE值总体呈减小趋势但不具规则性;若n固定不变,随着m值增加,RMSE值的变化具有波动性.因此,ntree与mdepth的参数选择会对RFR预测性能产生影响.采用IFOA算法对RFR模型中的ntree和mdepth进行参数寻优. 图5 不同ntree与mdepth时预测误差的均方根值Fig.5 RMSE of different ntree and mdepth 2) 参数设计 本文采用PSO-RFR、FOA-RFR、MFOA-RFR、RFR和SVM来对比分析IFOA-RFR模型性能. IFOA中指数因子P为0.8,λ为0.5;MFOA中固定搜索步长R为3,子种群数M为5;FOA中固定搜索步长R为3;PSO算法中粒子维数为2,惯性权重因子为0.8,加速因子c1与c2均为0.5;各优化算法中迭代次数Maxtimes为100,种群大小Popsize为30,n的寻优区间为[1,200],m的寻优区间为[1,3 000].在SVM中利用网格交叉验证法得到惩罚因子C为12.32,径向基核函数参数g为22.05. 3) 优化算法适应度分析 同时采用MFOA、FOA、PSO与IFOA进行RFR参数寻优,优化结果见表1. 表1 不同优化算法的寻优参数及性能对比 表1显示,FOA算法耗费的时间为67.886 0 s,RMSE为0.545 5,表明FOA算法收敛速度快但收敛精度低;MFOA算法的RMSE为0.503 6,表明MFOA较FOA在收敛精度上有所提升;IFOA的RMSE最小,为0.407 9,表明改进算法的收敛精度最高,虽然CPU时间较FOA和MFOA有所提升,但整体寻优效率良好.4种算法的适应度曲线如图6所示. 图6 适应度对比曲线Fig.6 Adapt ability contrast curve 分析图6,FOA算法在迭代初期就开始收敛,虽然收敛速度快,但适应度值低,说明易陷入局部最优.MFOA算法在迭代到3次时适应度值降低,在迭代到90次时收敛于0.472 2.PSO算法迭代到91次时收敛,适应度值为0.479 4.IFOA算法在迭代到4次时适应度值从0.484 1变化到0.474 4,在迭代到22次时适应度值有所降低,在迭代到59次时适应度值又减小0.002 4,最终在迭代到80次时收敛,说明了IFOA算法逐步逼近最优解,与其他算法相比,它具有更好的全局寻优和局部探索能力,且在收敛精度上都要优于其他几种算法. 图7是预测结果的点线图,实际值表示实际风速,b和c是各模型的局部扩大比较.观察b和c部分,当实际风速值突变时(如b中95到97,c中174到176),各模型预测效果越来越差,但IFOA-RFR模型在这些时刻的预测值最接近实际值,说明所提模型的预测精度更高,在预测中表现更好,保持了原始风速曲线的形状. 图7 风速预测曲线Fig.7 Wind speed forecasting curve 为进一步反映每个时刻的预测误差,计算各模型相对误差,误差值分布情况如图8所示. 图8 相对误差箱形图Fig.8 Relative error box plot 图8中箱体虚线范围代表最小值-最大值、“□”符号代表均值、“×”符号代表99%分位数,连线表示各模型相对误差值100%分位数连接线.从图8可以看出,IFOA-RFR模型每个预测点的相对误差均在50%以下,离散程度小于其他模型,这表明IFOA-RFR组合模型性能优于其他5种对比模型. 表2列出了各对比模型的预测误差,误差指标包括RMSE、MAE、MAPE. 表2 不同方法的预测误差 从表2可知,IFOA-RFR模型的RMSE、MAE、MAPE分别为0.407 9、0.287 7、6.9788,与其他模型相比具有最小的预测误差.与单个预测模型SVM、RFR相比,IFOA-RFR的MAPE分别降低了17.335%、7.323 7%.与优化算法PSO、MFOA和FOA相比,所提算法的RMSE分别减小了0.132 1、0.095 7、0.137 6.同时,IFOA-RFR的MAPE值比FOA降低了7.323 7%,RMSE和MAE分别降至0.464 5和0.309 0,说明改进后算法的整体预测精度得到了提高. 本文提出一种改进的果蝇算法优化随机森林回归模型,并将其应用到风速预测研究中,实验验证了该模型的可行性和有效性.结论如下: 1) RFR风速预测模型中参数ntree和mdepth的选择会对预测结果产生影响. 2) IFOA算法在FOA中引入函数机制使搜索步长自适应迭代更新,与PSO、MFOA、FOA算法进行收敛速度、收敛精度、算法运行时间的比较,改进算法有效提高了算法的寻优效率和全局寻优能力. 3) 选取风电场实际风速数据,利用IFOA-RFR模型对历史风速进行预测,以RMSE、MAE、MAPE、决定系数和相对误差为评价指标,对比PSO-RFR、MFOA-RFR、FOA-RFR、RFR、SVM的风速预测结果,表明IFOA-RFR具有更高的预测精度和更好的拟合度,证明了该模型在风速预测方面的可行性.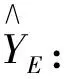
1.2 果蝇优化算法

Y(i)=Y+R1.3 改进的果蝇优化算法
2 IFOA-RFR风速预测模型
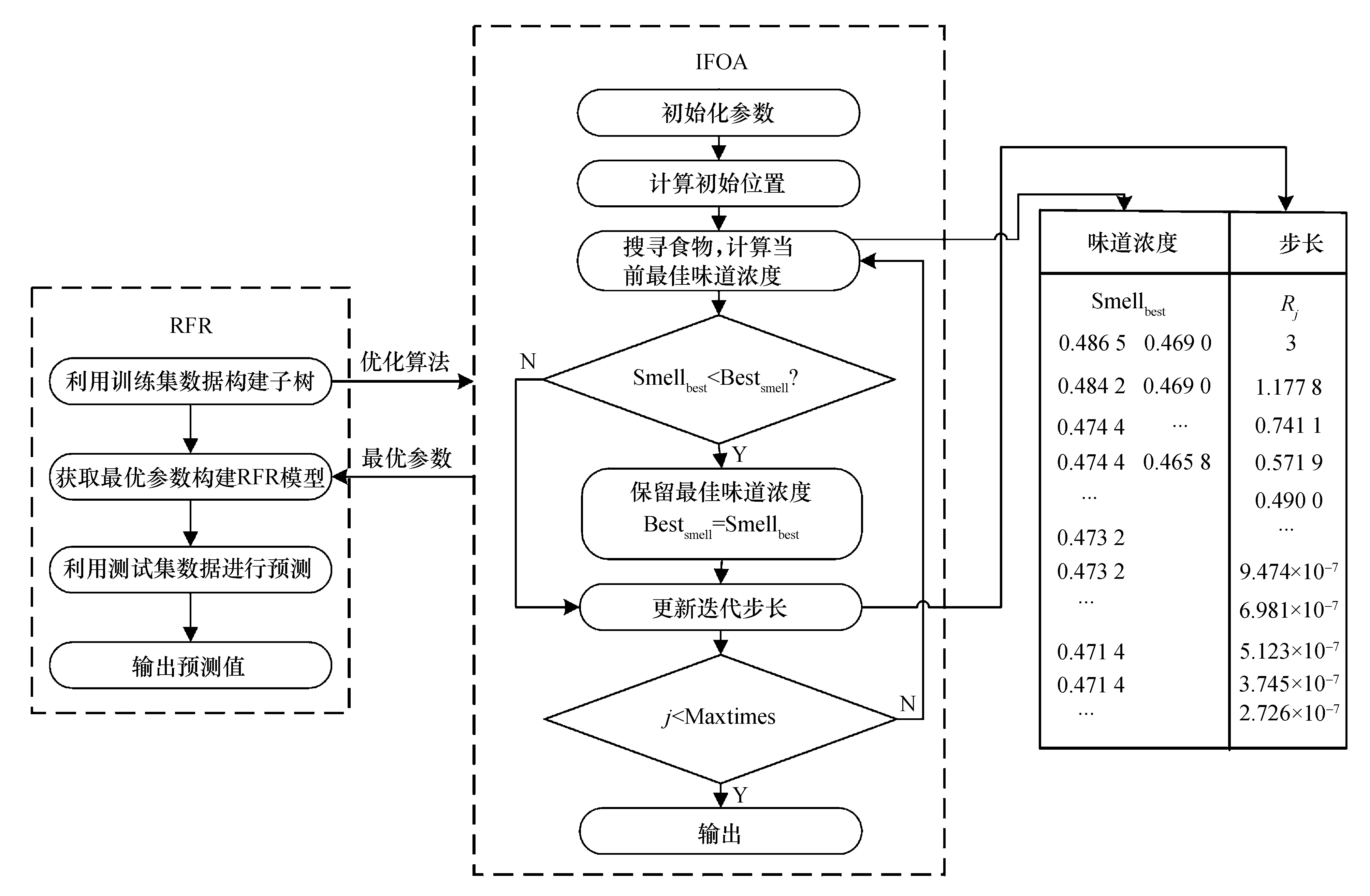
3 实验分析与比较
3.1 实验数据与评价指标


3.2 实验设计
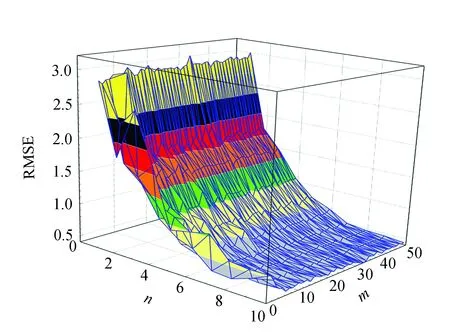

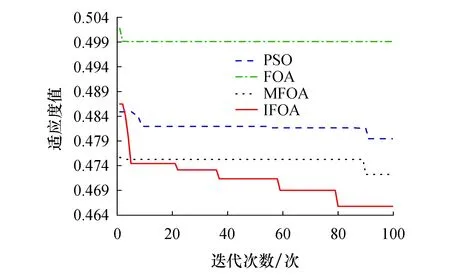
3.3 对比分析

4 结论
