应力比对铝钢复合材料界面Ⅰ型裂纹应力强度因子的影响

李有堂, 杨 龙

(兰州理工大学 机电工程学院, 甘肃 兰州 730050)

铝钢复合材料结合了钢的硬度强、防腐蚀和铝的质量轻、导电导热性强等特性.目前已经有很多文献研究了复合材料裂纹的应力强度因子.马振洲等[1]为研究界面裂纹动态应力强度因子在冲击荷载作用下的变化规律,利用双材料界面理论,推导出界面裂纹尖端的应力强度因子表达式.张硕[2]对垂直于界面的裂纹问题进行研究,采用有限元法计算垂直于界面的裂纹应力强度因子.杨军辉等[3]为求解裂尖位于界面上的垂直双材料界面裂纹应力强度因子,开发了一种加料有限元方法.李有堂等[4-5]根据双材料金属基体裂纹的断裂设计,建立了复合材料界面裂纹裂尖的应力场和位移场表达式,然后用有限元法分析了不同材料间基体裂纹的应力奇异性.李有堂等[6]还以铝钢爆炸焊复合板为研究对象,研究了Ⅰ型界面裂纹的扩展路径.张幸红等[7]对复合材料裂尖应力强度因子在机械载荷和热载荷等条件下的具体数值进行了计算验证.苏毅等[8]给出了分析双材料界面裂纹应力强度因子的广义扩展有限元法的基本原理,提出了一种新的双材料界面裂纹尖端富集函数.Kim等[9-10]比较了利用位移相关技术(DCT)、修正的裂纹闭合技术(MCC)和J积分技术计算复合材料裂尖应力强度因子的优劣,研究了各向同性、正交各向异性梯度复合材料中Ⅰ-Ⅱ复合裂纹的应力强度因子.Ayhan[11]运用强化有限元方法研究了三维复合材料中裂尖的Ⅰ型和Ⅰ-Ⅱ型复合裂纹的应力强度因子.

虽然界面裂纹应力强度因子的相关研究已经取得了一定的成果,但这些成果都没有考虑到应力比对界面裂纹应力强度因子的影响.因此本文以节点位移外推法计算界面Ⅰ型裂纹的应力强度因子,研究应力比对铝钢复合材料界面Ⅰ型裂纹应力强度因子的影响.

1 界面Ⅰ型裂纹应力强度因子的节点位移外推法

基于有限元思想,节点位移外推法的基本原理是用有限元法计算一些节点在界面裂纹尖端区域附近的位移,这些节点位于极角θ=π的界面裂纹表面上,如图1所示.图中a为裂纹长度,θ为裂纹扩展方向,r为节点到裂纹尖端的距离.通过求解得到的裂尖位移计算出这些节点的位移量,利用这些节点位移量表征应力强度因子,将这些表征应力强度因子进行最小二乘法拟合,将拟合数据外推求解得到界面裂纹尖端应力强度因子.

根据断裂力学可得复合材料界面Ⅰ型裂纹尖端场的位移场极坐标：

(1)

式中：i=1、2对应双层复合材料中的材料一和材料二；λ为应力奇异性指数,是一个与匹配材料有关的参数,由裂纹尖端奇异性决定；μi为剪切模量,可以通过其与弹性模量之间的关系μi=Ei/2(1+νi)得到；νi为泊松比；KⅠ为界面裂纹应力强度因子；gr和gθ为奇异位移场因子,可参照文献[4]获得,具体表达如下：

(2)

式中：ηi=νi(平面应变状态),ηi=νi/(1+νi)(平面应力状态)；F′i(θ)为Fi(θ)的一阶导数；Fi(θ)为结构所受载荷场,具体表达式如下：

(3)

式中ai、bi、ci、di为常数.λ可以从以下方程得到：

2αcos πλ-βλ2-γ=0

(4)

式中：α,β,γ,m都是奇异性指数特征方程的特征因子,由铝钢复合材料的材料参数弹性模量和泊松比决定,具体表达如下：

(5)

式中：k1、k2为铝钢复合材料的材料参数,ki=(3-νi)/(1+νi)(平面应力状态),ki=3-4νi(平面应变状态),i=1、2.

将各项材料参数按照条件代入式(5),求解得到α、β、γ、m；第二步把求解得到的α、β、γ、m代入式(4),解方程得到λ；第三步把θ=π和λ代入式(3)可以得到Fi(θ)；第四步把Fi(θ)代入式(2)解得gr的具体数值；最后将gr代入式(1)中的uir,由此得到位于界面裂纹上的节点位移与应力强度因子的关系：

(6)

将应用有限元法所求解出的位于θ=π界面裂纹上的一些节点位移分量数值(r,uir)代入式(6),求解出选取节点的表征应力强度因子：

(7)

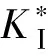
(8)

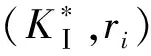
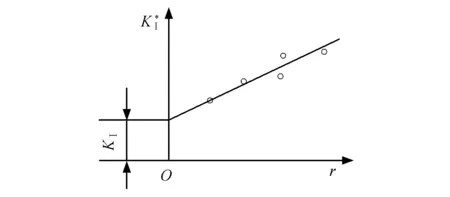
图2 节点位移外推求解KⅠFig.2 Node displacement extrapolation solution KⅠ

2 铝钢复合材料节点位移外推法的应用实例

2.1 几何模型

目前国内外采用焊接铝钢复合材料作为船舶过渡连接接头的连接方式.这种连接方式在改善铝、钢结合部的水密性、耐蚀性、简化施工工艺等方面较铆接具有显著的优点,而且其连接结构的强度,尤其是疲劳强度较铆接有很大的提高,疲劳寿命为铆接的10倍.因此,作为船舶中的重要结构,铝钢复合过渡接头的疲劳性能受到了船舶设计的普遍关注.本文以铝钢复合过渡连接接头的界面Ⅰ型裂纹为研究对象,几何尺寸如图3所示,裂缝长度为a,a/W的取值为0.3～0.8,三维建模如图4.铝钢复合材料的铝层弹性模量为66 500 MPa,密度为7 300 kg/m3,泊松比为0.31；钢层弹性模量为206 000 MPa,密度为7 930 kg/m3,泊松比为0.3.

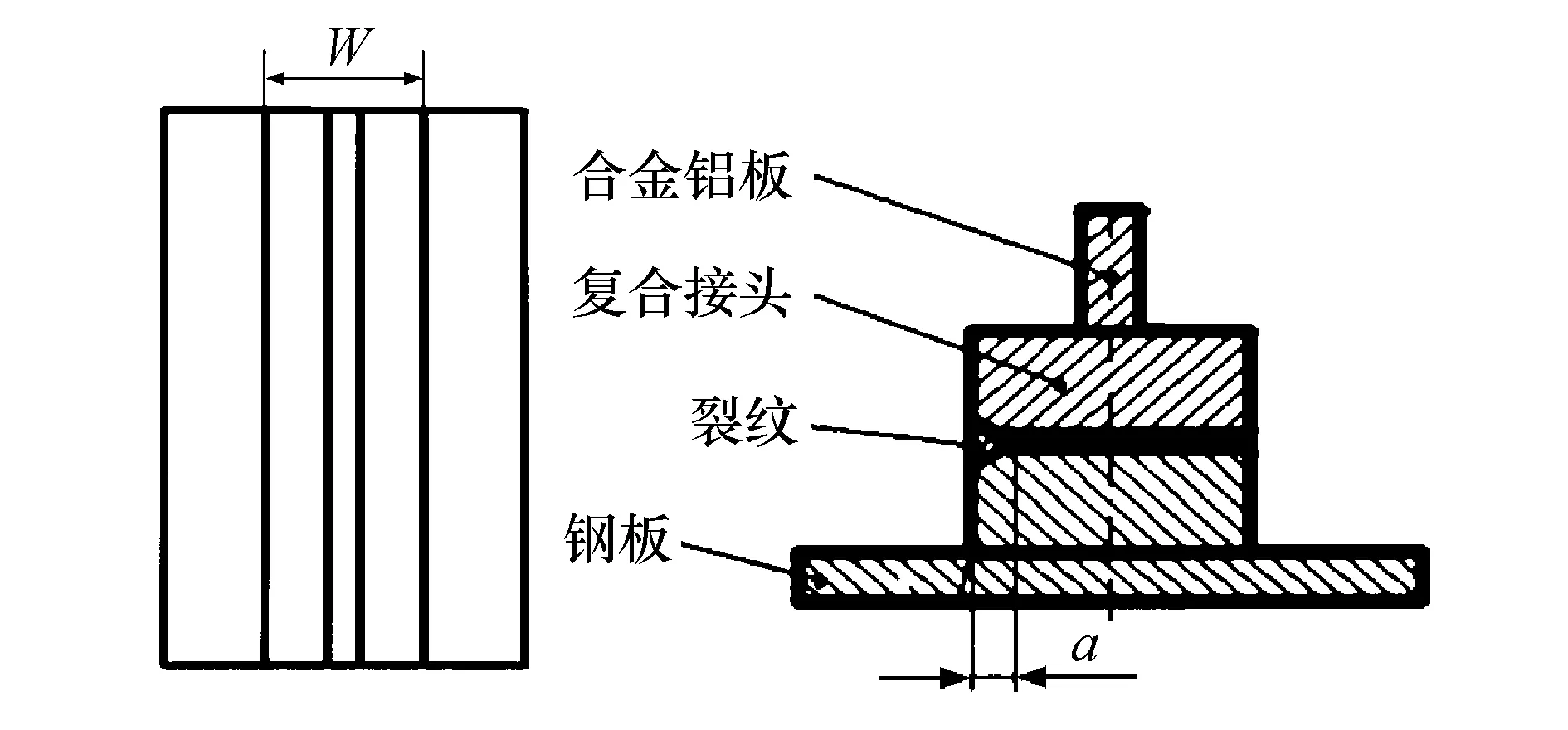
图3 船舶铝钢复合过渡连接接头示意图Fig.3 Schematic diagram of composite transition joint of ship aluminum and steel

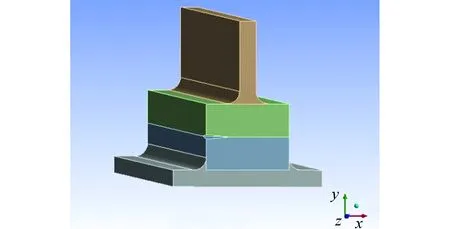
图4 过渡连接接头Ⅰ型界面裂纹三维建模Fig.4 3D modeling of mode-Ⅰinterface crack in transition joint

2.2 过渡连接接头有限元仿真分析

对于上述的三维模型,运用ANSYS软件进行仿真模拟.由于设定的铝钢过渡连接接头界面单边Ⅰ型穿透型裂纹为理想的尖锐裂纹,故此裂尖附近区域的应力梯度极大,而且裂尖位置还存在奇异性,不可忽略.因此,通过对裂纹尖端附近区域的网格进行细化来提高仿真精度.由于a/W的值不同,导致每个a/W的建模都不相同,网格的划分也不同.例如a/W为0.3时网格划分为292 368个网格、513 443个节点.模型的网格尺寸类型如图5所示.

图5 a/W=0.3时的模型整体网格

铝钢复合材料过渡连接接头的受载荷情况包括：底板的钢甲板固定；顶端的铝板受到竖直y方向的周期性拉伸载荷σ作用,因为实际情况较为复杂,且缺乏规律性,所以将其实际受载简化为有规律的周期性等幅载荷.为便于研究应力比对界面裂纹应力强度因子的影响规律,载荷谱参照文献[12],如图6所示.

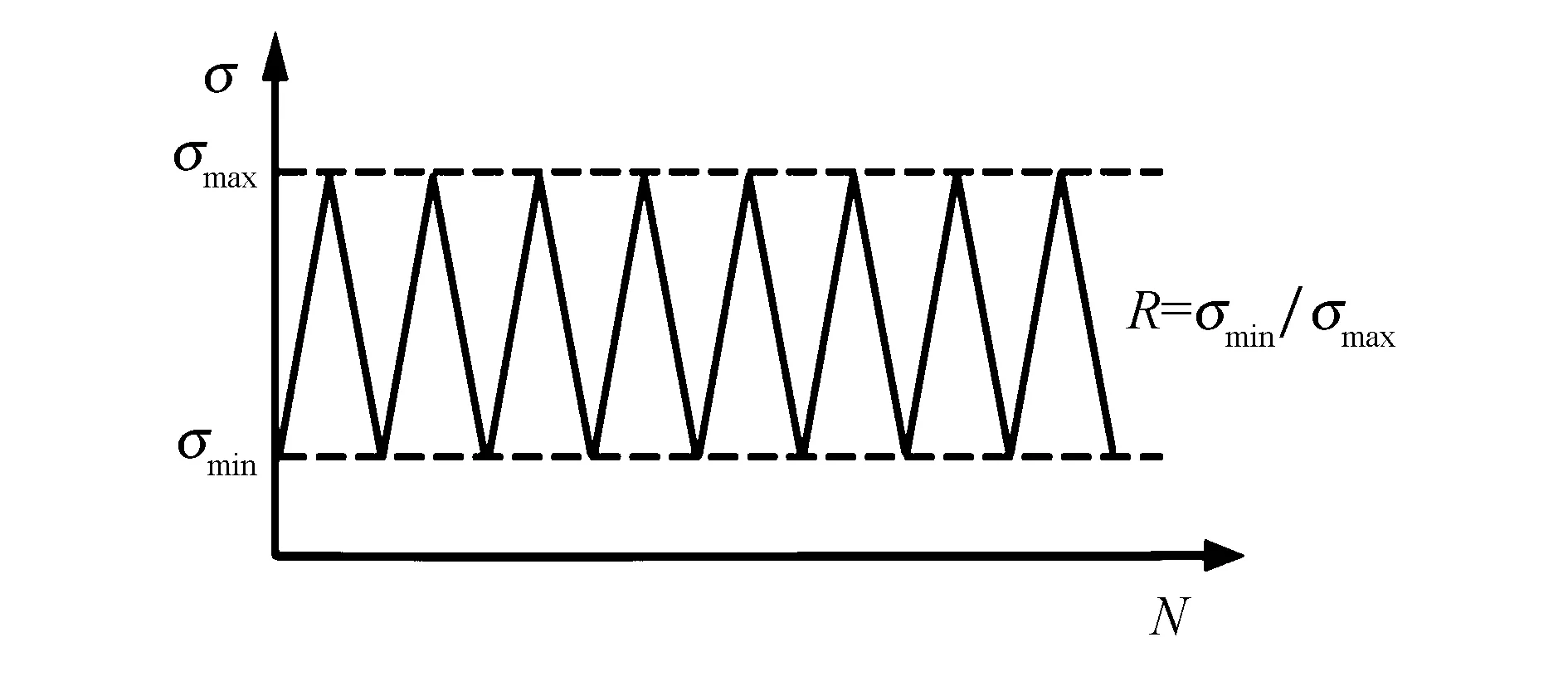
图6 周期性等幅循环载荷谱Fig.6 Cyclic load spectrum of cyclic isoamplitude

加载周期性等幅载荷谱的数学表达式为

(9)

式中：y1表示斜率为正的加载曲线;y2表示斜率为负的加载曲线;T为周期，f为频率,则T·f=1;t为时间;σmax为最大载荷;σmin为最小载荷;k为常数(k=0,1,2,3,…).

为了比较不同应力比R界面Ⅰ型裂纹应力强度因子的作用结果,R分别定义为0.1、0.3、0.5,载荷如表1所列.

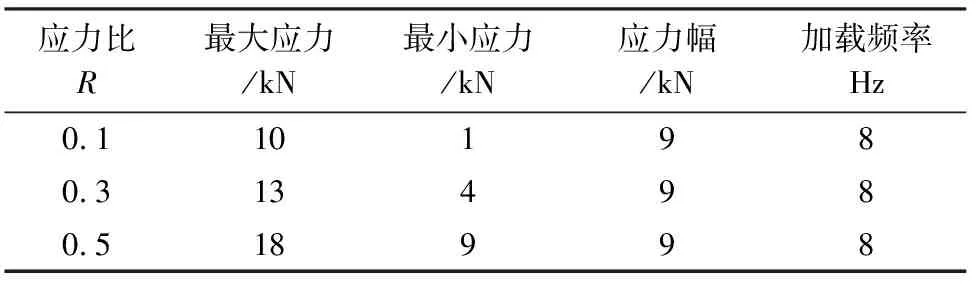
表1 载荷参数值

按照以上规定的边界约束条件,对外部加载情况进行有限元仿真模拟,求解裂尖的应力场以及位移场.图7为应力比R=0.3时,周期性等幅加载条件下,裂纹尺寸比a/W为0.3时的过渡连接接头界面裂纹尖端的应力场和位移场云图.

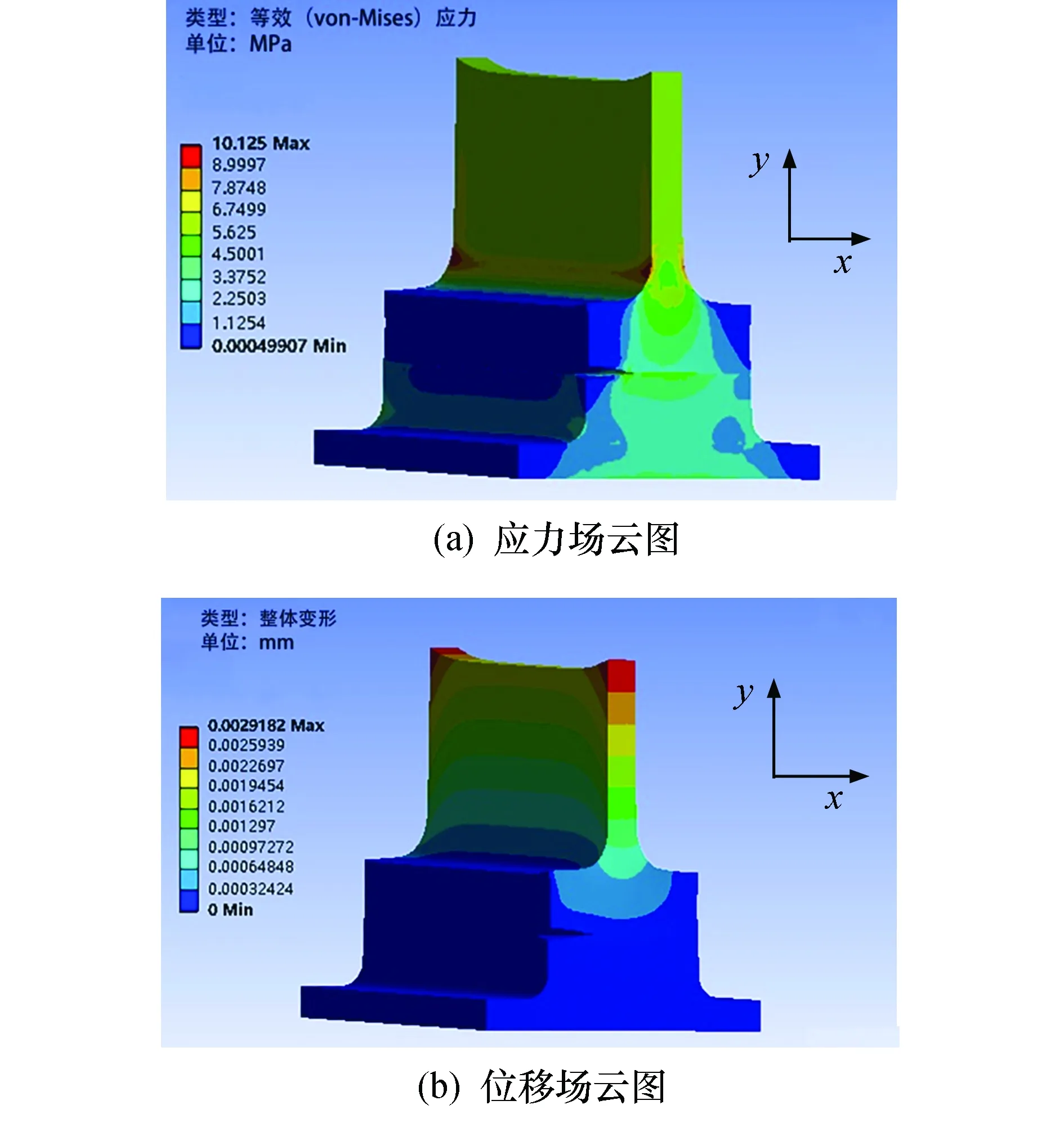
图7 R=0.3、a/W=0.3时的应力场和位移场云图Fig.7 Stress field and displacement field cloud diagram when stress ratio R=0.3 and a/W=0.3

在ANSYS中根据图7b位移场云图,导出应力比R=0.3、a/W为0.3时所有节点的位移场分量值.然后根据节点位移外推法的操作要求,以铝钢复合材料过渡连接接头界面裂纹尖端为极坐标原点,分别在θ=0和θ=π两个方向上，选取不同r处裂尖附近节点的位移场分量值，如表2所列.

表2 R=0.3、a/W=0.3时的节点位移值

3 应力比对铝钢复合材料界面Ⅰ型裂纹应力强度因子的影响

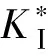
图8 不同应力比R、不同a/W下界面Ⅰ型裂纹的应力强度因子KⅠFig.8 KⅠ of interfacial mode-Ⅰ crack under different stress ratios R and a/W

从图8可以得到:在同一裂纹尺寸比a/W条件下,裂纹的应力强度因子KⅠ随应力比R的变大而变大；在同一应力比R条件下,裂纹的应力强度因子KⅠ和裂纹尺寸比a/W为正相关的关系,即裂纹长度越长,铝钢复合材料界面裂纹裂尖应力强度因子越大.

4 结论

利用求解铝钢复合材料的界面Ⅰ型裂纹应力强度因子的节点位移外推法，对包含Ⅰ型界面裂纹的铝钢复合材料进行有限元仿真分析,得到铝钢复合材料界面Ⅰ型裂纹裂尖的位移场分量,代入节点位移外推法求解得应力强度因子.最后对求解结果分析讨论,得到以下结论：

1) 应力比和裂纹尺寸比两个因素都将会对铝钢复合材料的界面Ⅰ型裂纹的应力强度因子产生作用;

2) 同一应力比时,应力强度因子与裂纹尺寸比呈正相关,即应力强度因子与裂纹长度同步变化；

3)不同应力比、同一裂纹尺寸比时,应力强度因子随着应力比的增大而增大；

4)不同应力比、不同裂纹尺寸比时,若裂纹尺寸比小于等于0.6,应力强度因子增幅不是很明显,若裂纹尺寸比大于0.6,应力强度因子增幅显著,且应力比越大增幅越快.