基于PLS的增压锅炉运行失稳概率修正计算

郑奕扬，倪 何，金家善

(1.海军工程大学 动力工程学院，武汉 430033; 2.海军工程大学 船舶与海洋学院， 武汉 430033)

1 引言

增压锅炉是蒸汽动力系统中的重要设备，主要作用是产生蒸汽供给主机做功，输出功率推动舰体运动。锅炉水位和汽压反映了锅炉的运行稳定性，通过计算锅炉水位和汽压超过极限值的失稳概率评估锅炉的运行稳定性。

在以预测趋势值为均值，以原时序的方差为方差，通过正态分布函数计算失稳概率的过程中，只考虑到了锅炉水位和汽压历史数据对于失稳概率的影响。由于增压锅炉的运行与其辅助设备具有耦合性，在未来一段运行时间内，锅炉水位和汽压相关参数的变化值将对失稳概率的计算产生影响。在趋势提取与预测方面，中值回归经验模态分解(MREMD)[1]是经验模态分解(EMD)[2-3]的优化算法，解决了端点效应问题。奇异值分解(SVD)[4,5]可以进一步提取分量中的隐藏趋势项。差分整合移动平均自回归模型(ARIMA)[6]是经济学中广泛运用的预测模型。多元统计数据分析方法分为2类:一类通过分析自变量和因变量的数据，寻找自变量与因变量之间的联系，主要包括回归分析以及判别分析；另一类通过分析所有变量间的相关性，对同类变量分析总结，主要包括主成分分析[7]、聚类分析以及典型相关分析[8]。偏最小二乘回归[9-10]结合了多元线性回归分析、主成分分析和典型相关分析方法的优点，得到了广泛运用。

本文将运用PLS方法得到锅炉水位和汽压的相关参数对水位和汽压的影响大小，以此修正失稳概率的计算区间，从而修正失稳概率。并基于实装运行数据计算得到锅炉水位和汽压的失稳概率，对于增压锅炉的运行稳定性做出评估分析。

2 锅炉水位和汽压的相关参数分析

对于增压锅炉来说，产生蒸汽以供各用汽设备使用是其最根本的功能，增压锅炉稳定产生蒸汽的能力决定着增压锅炉的运行稳定性。锅炉汽压反映了锅炉内蒸汽的压力，代表着锅炉的蒸汽输出能力，锅炉汽压越低，锅炉的蒸汽输出能力越小，锅炉汽压越高，锅炉的蒸汽输出能力越大。锅炉水位反映了锅炉内炉水的储备量，影响着锅炉产生蒸汽量的大小。因此锅炉汽压和锅炉水位反映了锅炉的运行稳定性。而蒸汽能否稳定产生同时也取决于锅炉中空气、燃油和给水的稳定供给。

2.1 锅炉水位的相关参数分析

锅炉水位的稳定与锅炉给水调节阀开度、给水机组转速和主机正车执行器开度相关，如图1所示。

图1 锅炉水位与相关参数的关系框图

根据增压锅炉的工作原理，给水调节阀位于增压锅炉前的给水管路上，控制着进入锅炉的给水流量。当阀门开度增大时，进入锅炉的给水流量增加；当阀门开度减小时，进入锅炉的给水流量减小。给水机组转速决定了给水调节阀两端的压差，影响着进入锅炉的给水流量。当给水机组转速增加时，给水调节阀两端的压差增大；当给水机组转速减小时，给水调节阀两端的压差减小。主机正车执行器开度决定了主机的运行工况，而主机工况值的高低决定着主机耗汽量的大小。因此当主机正车执行器开度增大时，主机耗汽量增加，需要增压锅炉提供更多的蒸汽，锅炉内炉水消耗量增加，从而使得水位下降；当主机正车执行器开度减小时，主机耗汽量减小，需要增压锅炉提供的蒸汽量减少，锅炉内炉水消耗量减少，从而使得水位上升。

2.2 锅炉汽压的相关参数分析

锅炉汽压的稳定与燃油流量调节阀开度、涡轮增压机组转速和主机正车执行器开度相关，如图2所示。

图2 锅炉汽压与相关参数的关系框图

根据增压锅炉的工作原理，炉膛内燃烧的稳定性决定着锅炉汽压的稳定性，良好的助燃空气、燃油与炉水的配比决定着燃烧能否稳定进行。燃油流量调节阀位于锅炉前的燃油管路上，控制着进入锅炉的燃油流量。当阀门开度增大时，进入锅炉的燃油流量增加；当阀门开度减小时，进入锅炉的燃油流量减小。涡轮增压机组与锅炉的进气口连接，当涡轮增压机组转速增大时，压气机输出功率增大，进入炉膛的助燃空气流量增加；当涡轮增压机组转速减小时，压气机输出功率减小，进入炉膛的助燃空气流量减少。主机正车执行器开度决定着主机的耗汽量，主机耗汽量越大锅炉汽压越低。在锅炉给水流量保持不变的情况下，若锅炉汽压上升，炉水的沸点降低，若保持锅炉产汽量不变，消耗的炉水增加，锅炉的水位下降。

3 修正失稳概率的计算

3.1 基于MREMD的参数变化值计算

锅炉水位和汽压及其相关参数的变化值计算步骤如下。

步骤1对于锅炉水位和汽压及其相关参数的时间序列分别进行MREMD分解，得到IMF分量imf(t)及残余分量re(t)如式(1)所示；将其残余分量re(t)视作固有趋势项，并取其一阶差分得到dre(t)，如式(2)所示。

s(t)=∑imf(t)+re(t)

(1)

dre(t)=diff[re(t)]

(2)

式(2)中：diff表示一阶差分计算。

步骤2为了简便计算，对于dre(t)进行预处理，运用信号抽取的方法，对其进行重新采样，剔除不需要的点，等间隔地抽取数据，如式(3)所示。

ddre(t)=dre(Mt)

(3)

式(3)中：M为抽取因子；ddre(t)为预处理后的时序。

步骤3取抽取因子为5，最终得到锅炉水位和汽压相关参数的关系如图3所示。

图3 相关参数曲线

3.2 基于PLS的拟合函数计算

运用偏最小二乘回归分析的方法，得到锅炉水位变化值与给水调节阀开度、给水机组转速、主机正车执行器开度变化值的拟合关系式和锅炉汽压变化值与燃油流量调节阀开度、涡轮增压机组转速和主机正车执行器开度变化值的拟合关系式。具体的计算步骤如下。

3.2.1数据标准化处理

以锅炉水位和汽压为因变量y，相关参数为自变量x，按式(4)进行标准化处理，得到因变量矩阵Y和自变量矩阵X为：

(4)

(5)

Y=ym,X=(xm1,…,xmk)T

(6)

3.2.2提取主成分

按照主成分分析的思路，提取拥有最大方差值的自变量矩阵X的主成分，同时，对矩阵Y需要拥有较强的解释能力，按照典型相关分析的思路，与矩阵Y应该取最大相关系数值。得到相关系数向量R为：

R=[ρ(xm1,ym),…,ρ(xmk,ym)]

(7)

式(7)中：k为自变量个数；ρ为相关系数。

计算得到第一个主成分t1为：

(8)

式(8)中：‖R‖2为R的2范数。

对X和Y分别作关于t1的回归，有：

X=αt1+X1，Y=βt1+Y1

(9)

式(9)中：X1和Y1为残差矩阵；α和β为回归系数，根据最小二乘法计算得到。

从残差矩阵X1和Y1中继续提取主成分，重复上述计算过程，利用偏最小二乘回归中的交叉有效性确定提取主成分的个数，从而停止计算。对锅炉汽压和水位及其相关参数提取主成分，得到t[1]与u[1]的线性关系如图4所示。

如图4可见，锅炉汽压和水位及其相关参数之间为近线性关系，因此可以认为建立的线性拟合模型是合理可行的。

图4 主成分线性关系曲线

T2椭圆图可以反映95%的置信度水平下样本的分布情况，对锅炉汽压和水位及其相关参数提取主成分，剔出那些与样本平均水平差别较大的特异点，绘制T2椭圆图如图5所示。

如图5可见，绝大部分样本点均落于椭圆内，因此可以认为样本数据的分布是合理的。

图5 T2椭圆图

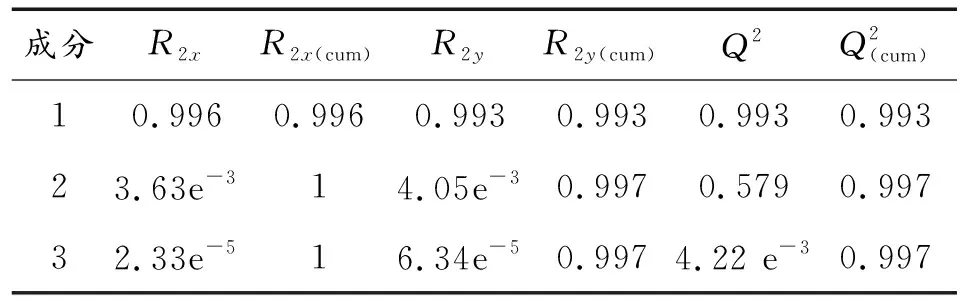
表1 锅炉汽压的交叉有效性分析指标

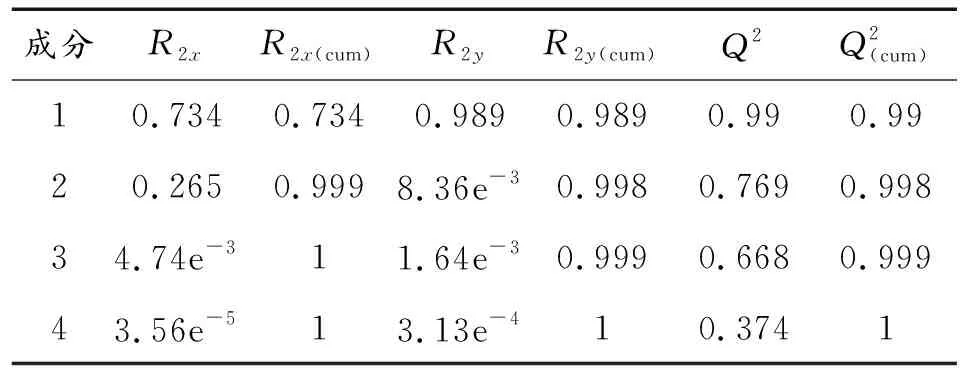
表2 锅炉水位的交叉有效性分析指标

3.2.3拟合函数计算

通过交叉有效性确定主成分后，利用确定的主成分对因变量矩阵Y进行线性回归分析，得到回归方程为：

Y=(xm1,…,xmk)·γ

(10)

式(10)中：γ为回归系数矩阵。

对矩阵X和Y进行逆标准化处理，得原数据的回归方程为：

Y0=X0γ0+ε=(x1,…,xk)·γ0+ε

(11)

式(11)中：X0和Y0为逆标准化处理后的自变量矩阵和因变量矩阵；γ0为逆标准化处理后的回归系数矩阵；ε为常数项。

对于锅炉汽压和水位及其相关参数的变化值，得到的拟合结果如图6所示，拟合值与原数据值的分布均分布在对角线附近，锅炉水位的拟合RMSEE为0.013 09，RMSECV为0.015 39，锅炉汽压的拟合RMSEE为8.561 1e-4，RMSECV为8.5671 e-4，拟合结果较好。

图6 拟合结果的分布曲线

3.3 失稳概率的修正计算

3.3.1获取预测趋势

选取增压锅炉运行过程中接近不稳定的实装运行数据，对其MREMD分解结果进行SVD分解，得到奇异值分解分量并计算每个奇异值分量的排列熵PE，选取排列熵小的分量运用ARIMA模型进行预测，重构得到预测趋势如图7所示。

图7 锅炉汽压和水位的预测趋势曲线

其中L为锅炉水位，Lmin为锅炉水位的低位极限值，P为锅炉汽压，Pmax为锅炉汽压的高位极限值，锅炉水位呈上升趋势，锅炉汽压呈下降趋势。

3.3.2计算失稳概率及其修正结果

对于锅炉汽压和水位的预测趋势，根据动态正态分布计算其失效概率为：

Li～N(Li,δL)，Pi～Pi(Pi,δP)

(12)

pL=p{Li≥Lmax∪Li≤Lmin}

(13)

pP=p{Pi≥Pmax∪Pi≤Pmin}

(14)

pplsl=p{Li≥Lmax-plsLi∪Li≤Lmin+plsLi}

(15)

pplsP=p{Pi≥Pmax-plsPi∪Pi≤Pmin+plsPi}

(16)

式(12)～(16)中：Li和Pi为第i秒的预测水位和汽压；δL和δP为锅炉水位和汽压的方差；Lmax、Lmin、Pmax和Pmin分别为锅炉水位和汽压的极限值；plsLi和plsPi为第i秒时相关参数变化对锅炉汽压和水位的影响值；pL和pP为锅炉水位和汽压的失效概率；pplsl和pplsP为锅炉水位和汽压的修正失效概率。

锅炉汽压和水位的概率及其修正结果如图8所示。

图8 失稳概率及其修正结果

由失稳概率的计算结果来看，锅炉汽压的失稳概率不超过0.45，锅炉水位的失稳概率不超过0.3，说明前者的稳定性低于后者。随着时间的推移，锅炉汽压和锅炉水位的失稳概率均下降，说明锅炉处于一个渐趋稳定的变化过程中。

在前15 s锅炉汽压相关参数的变化趋势将引起锅炉汽压上升，因此失稳概率增大；在后75s锅炉汽压相关参数的变化趋势将引起锅炉汽压下降，因此失稳概率减小；而锅炉水位相关参数的变化趋势将引起锅炉汽压上升，因此失稳概率增大。

4 结论

采用MATLAB 2016a完成代码编写与计算，运用SIMCA软件进行偏最小二乘回归分析。根据正态分布的特征可知，当失稳概率大于0.5时，锅炉汽压和水位已超过极限值，此时会触发保护装置导致锅炉停止工作。锅炉汽压和水位的失稳概率的修正计算结果显示，在未来的90 s运行时间内，锅炉水位最大修正失稳概率为0.250 6，最大失稳概率为0.222 5；锅炉汽压最大修正失稳概率为0.441 7，最大失稳概率为0.394 7。增压锅炉的运行处于极度不稳定的状态，失稳概率的修正计算结果更能反映增压锅炉的实际运行稳定性。研究成果可为蒸汽动力系统的运行稳定性评估奠定基础。