基于区域点云的工件位姿计算方法

乐 英，赵志成

（华北电力大学能源动力与机械工程学院，河北保定071000）

随着工业4.0进程的不断推进，企业的生产模式正经历着由传统模式向自动化、智能化模式转变。在这一转化过程中，通过工业相机获取所需要的物体信息研究成为了一个重要的研究领域。

在机器人抓取任务时，不仅能够抓取到物体，同时也要求机器人以某样的姿态去完成抓取任务，这就要求在获取空间位置信息的同时也要获取目标物体的姿态信息。在获得物体的空间位置信息的基础上，周凡桂等［1］提出一种基于编码合作标志点的方法估计目标位姿。通过将标志点布置于模型表面，运用立体匹配技术和绝对定姿算法求解相对位姿初值，并进行误差优化。虽然这种方法可以获取精度较高的物体位姿，但是主要依赖于所布置的标志点，然而，在实际的生产过程中，文中所提的条件是不易满足的。蒋萌等［2］根据标定的结果对选定的特征点进行三维重建，并根据选定的特征点在图像和实际场景中对应的2D-3D位置信息求解目标位姿，但是这种根据选定的几个特征点对获取的位姿矩阵在文中进行反向验证时，Z轴的误差最大达到了4.604 mm。Pas等［3］提出了基于几何条件约束的检测方法，其主要思想是在物体上定义若干几何条件为后续计算目标最佳抓取位姿提供约束条件。近些年来，随着深度学习的快速发展，也有学者将深度学习应用到物体位姿估计领域中。文献［4］提出了一种多模特征深度学习构建叠层深度网络实现抓取位姿最优判断。文献［5］训练了一种轻量级的GG-CNN，以深度图作为网络模型的输入，端到端输出每一个像素上的抓取位姿。但是，基于深度学习的位姿检测算法主要依赖于构建的数据集，数据集的规模和质量直接影响检测结果的准确性。

根据以上问题，为了获取物体的稳定可靠的位姿信息，本文将结合机器人的实际工作环境，基于物体的点云特征信息对目标物体的位姿计算进行研究。

1 基于双目的零件位姿检测

为了从图像中获取目标物体的三维信息，根据相机的成像原理，通过构建相似模型检测左右成像面中同一个物体成像点的视差，采用相似原理计算出该物体点在相机坐标系下的深度信息，同时根据已经获取的深度信息计算该物体在相机坐标系下的三维点云。

1.1 相机模型

通过对相机进行标定获取相机的内外参数，建立图像坐标与相机坐标系以及世界坐标系之间的转换关系，进而通过转换关系获取三维空间中物体在图像中的二维位置关系。理想的双目相机模型如图1所示。图中：f为相机的焦距；Ol为左相机的光心；Or为右相机的光心；P（x，y，z）为空间中的一个点，在左相机的成像点为PL，在右相机的成像点为PR；XL为左成像点在相机坐标系下距离图像左边缘的距离；XR为右成像点在相机坐标系下距离左边缘的距离。两个光心之间的距离（x11+x22）为两个相机的基线距离，用B表示。

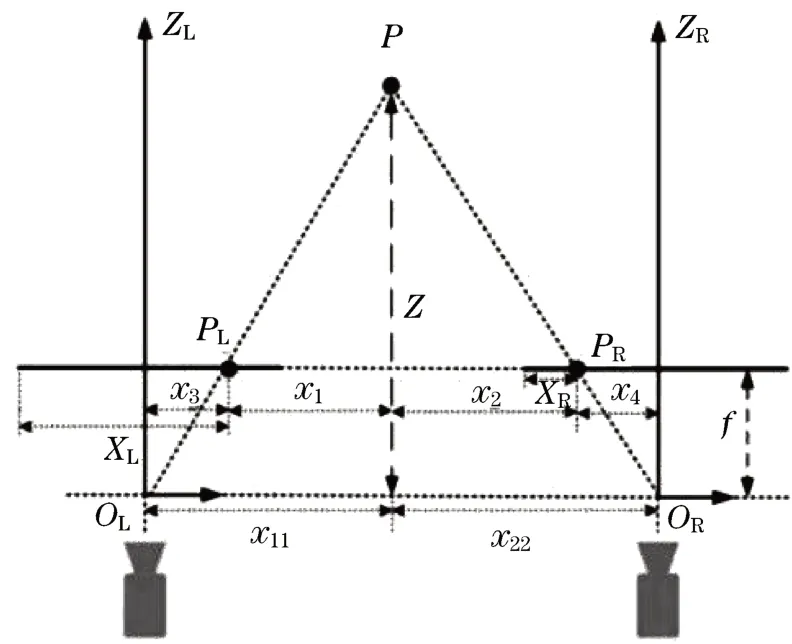
图1 面阵相机理想模型Fig.1 Optimal model of phase matrix

世界坐标系下的点P在投影到相机的成像面这一过程涉及世界坐标系、相机坐标系和图像坐标系的转换，具体转换过程如下：

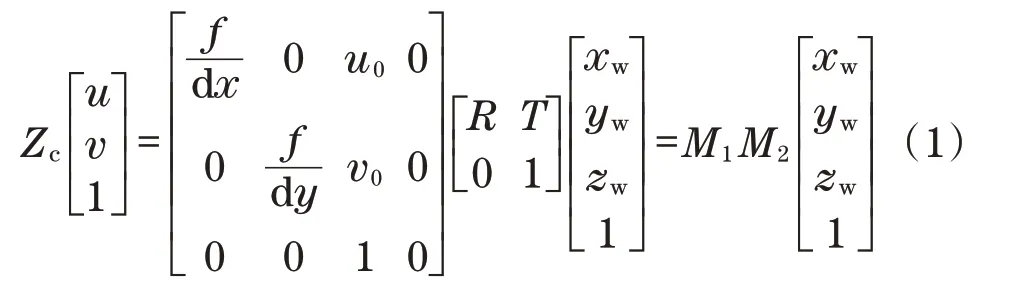
式中：M1为相机内参矩阵；M2为相机外参矩阵。因此，可以建立世界坐标系与图像坐标系之间的转换关系。

1.2 特征匹配与深度优化

为了获取工件的三维点云，对比分析这里选用的BM图像特征立体匹配算法计算视差［6-8］，从而获取工件的三维坐标值。

根据实际生产环境中物体所在的背景固定这一特性，采用背景差分法分割图像上的目标物体，获取物体在图像上分布的坐标信息，以获取的坐标值进行目标物体区域划分，获取目标物体的特征信息，采用BM算法对两种方法处理后的数据进行特征匹配，结果如图2和图3所示。

图2 去噪深度图图Fig.2 Denoise depth map

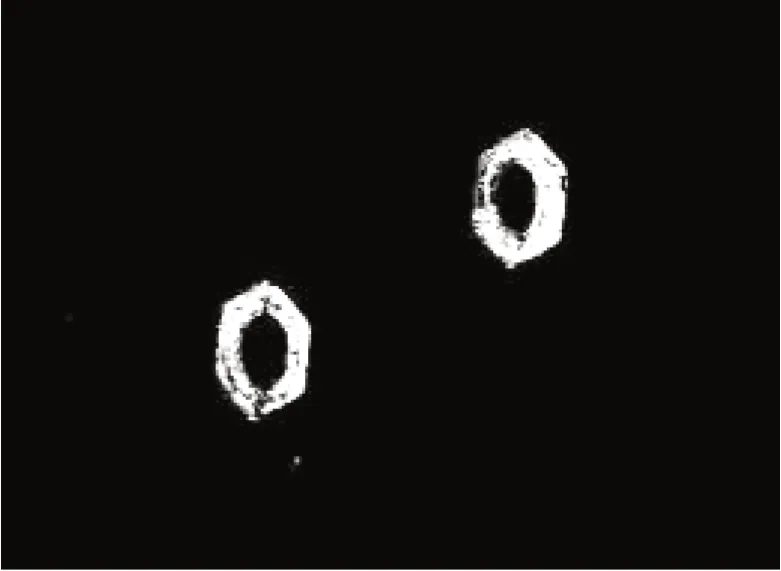
图3 差分深度图Fig.3 Differ ential depth map

可以看出，本文所用的方法可以在较少的噪声干扰下获取丰富的物体深度信息，并且深度图中孤立的深度孤立点也得到了很大的抑制。根据得到的物体特征点视差，通过如下公式即可以获取目标物体在相机坐标系下的粗糙点云集：

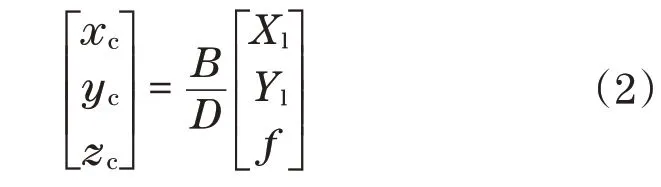
式中：D为同一目标点对应的视差；Xl和Yl为左相机图像坐标系中的坐标值；xc、yc、zc表示在相机坐标系下的坐标值。

为了消除由于匹配误差所带来的深度噪声，在深度空间对物体的深度信息进行去噪处理。为了不失去目标边缘特征深度，同时可以有效地抑制孤立的深度值点，采用3层金子塔求和算子对深度图进行卷积采样，获取每个采样点邻域内的点集分布状态，去除孤立的深度特征点结果如图4所示。

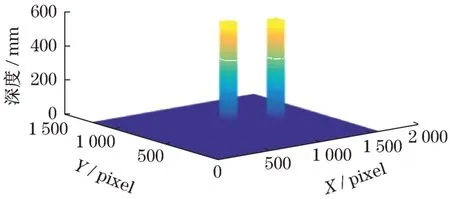
图4 优化后的深度图Fig.4 Optimized depth map

1.3 位姿特征点计算

为了在获得的物体点云集中获取能够代表物体的特征点，计算获取的特征点深度梯度，并根据梯度值进行聚集获取可靠稳定的特征点。设深度图像为H（x，y），这里通过如下公式计算深度特征值2个方向的梯度值：

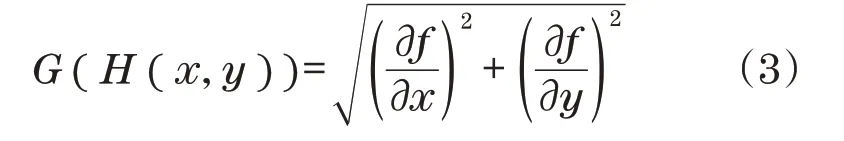
在深度图中，相邻两个点的图像量度为1，根据导数定义分量可写为

对每一个特征点深度值进行梯度计算，并对梯度值进行分类，结果如图5所示。

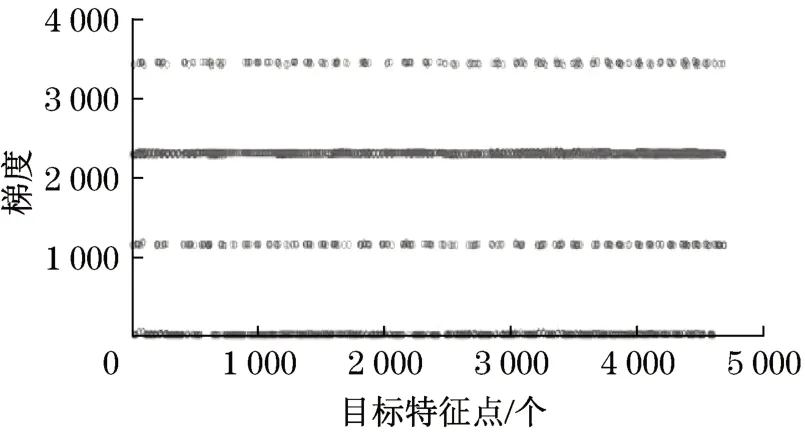
图5 深度梯度分布Fig.5 Depth gradient distribution

根据梯度分布可以得到物体的边缘和非边缘信息，根据连续的平面深度变化幅度小这一特性进行深度密度检测，将深度密度小的区域进行抑制，以获取稳定可靠度高的深度特征点进行位姿计算。

1.4 坐标系建立与姿态估计

根据刚体旋转平移内部特征点相对位置不变的特性，在经过1.2节方法优化后的点云集中，获取可以代表物体平面的特征点。这里根据物体表面的几何形状进行均匀分割，获取4个区域R1、R2、R3和R4。在这4个区域内分别对内部的点云集进行平滑处理，通过如下公式求取局部均值作为该区域的初始参考特征点：

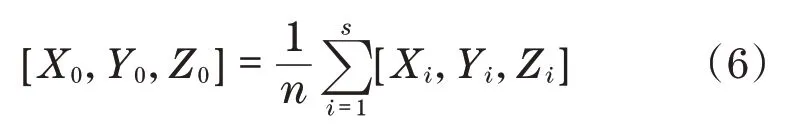
式中：X0、Y0、Z0为参考特征点；Xi、Yi、Zi为区域特征点；s为区域特征点数量。

为了获取稳定且具有代表性的特征点，以初始特征点作为参考点，建立如下D-D评价函数：

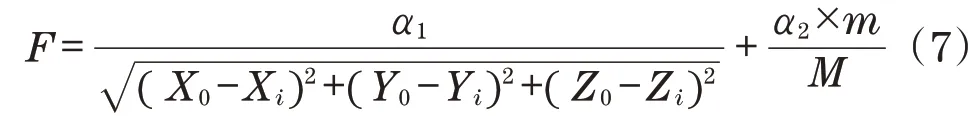
式中：α1和α2为比例系数；m为待评价特征点的深度值在其±amm范围内的点云数量，a的值取决于区域范围内点云的深度变化幅值；M为区域内总点云数量。

该函数共有2个部分：第1部分为区域内的点云与特征点的绝对距离；第2部分为点云深度密度，加入点云密度是为了防止距离参数被独立的奇异特征点影响。将最大F值对应的特征点作为该区域的表示点P1、P2、P3和P4。

为了描述物体在相机坐标下的位姿，建立物体的坐标系OT（x，y，z）。以其中一个点为坐标原点，同时在P1P2P3组成的平面H上，将P1P2向量单位化作为X轴，根据如下公式求出平面的法向量：

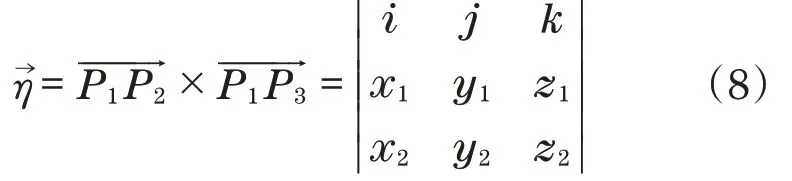
以P1点作为原点建立Z轴，根据右手定则，在平面H上以P1点为原点，建立Y轴，结果如图6所示。

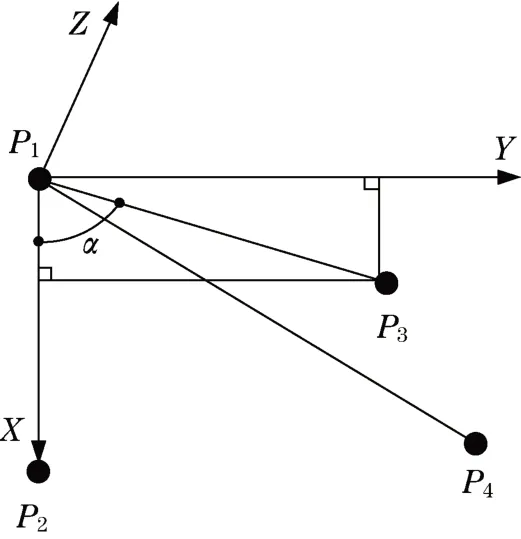
图6 物体坐标系Fig.6 Physical coordinate system

在建立的物体坐标系下描述所挑选出来的4个特征点，通过如下公式求取：

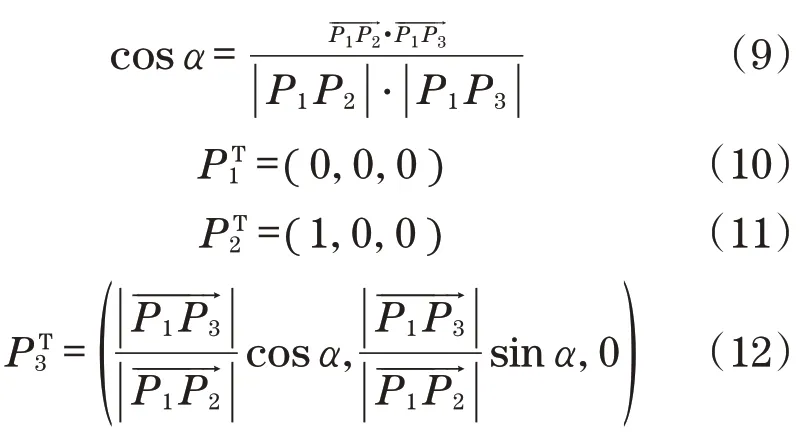
P4在工件坐标系下的描述如图7所示。图中，a、b和c分别为与3个轴的夹角。根据式（9）可以获取各个夹角的余弦值，归一化P1P4的模长，可以获得P4在工具坐标系下的描述，同时根据P4点的计算，可以计算任意的特征点在工件坐标系下的描述。

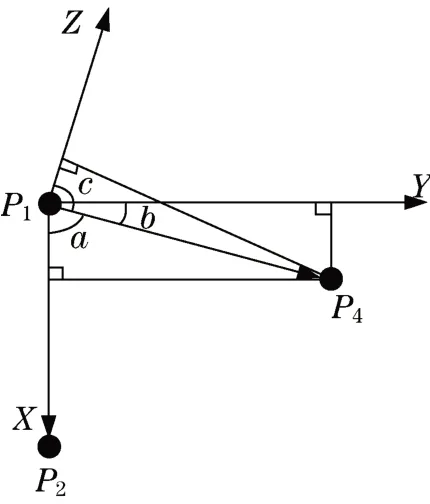
图7 特征点描述Fig.7 Description of feature point

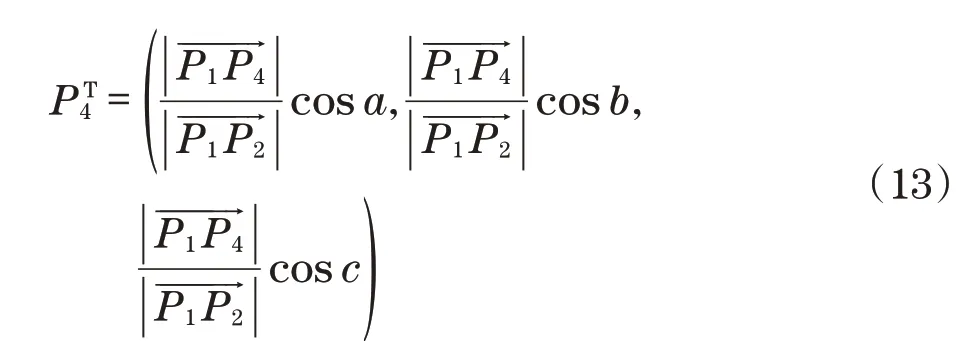
此时，已知4个目标点在相机坐标系下的坐标值Cm和4个点在物体坐标系下的坐标值Tm，通过如下公式可以建立工件坐标系与相机坐标系的变换关系R：

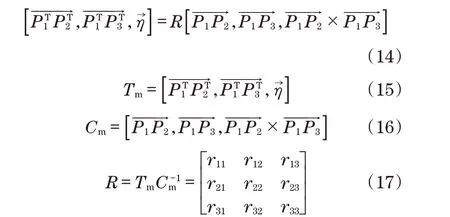
根据如下公式建立平移向量T：

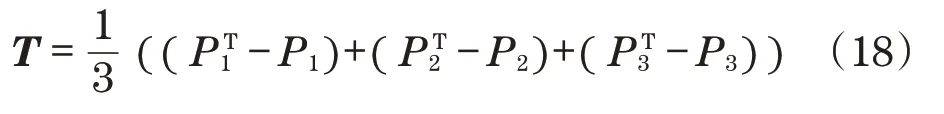
根据所获得的R，以及X-Y-Z固定角表示法，通过如下公式获得回转角γ、俯仰角β和偏转角α：

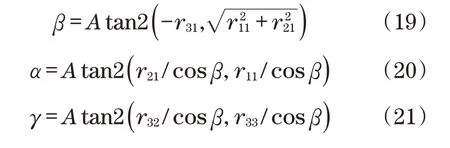
2 试验验证与分析

2.1 实验环境与数据处理

图像采集设备采用的是德国Basler acA1600-20 gm面阵双目工业相机，采用Matlab、Pycharm编译环境下的Python 3.6和Opencv 3.4.2，实现对目标物体位姿的检测和计算。相机与工作台的垂直距离为591 mm，采用厚度为15.8 mm的螺母零件作为试验对象并进行数据采集。

将处理好的左右相机图像进行立体校正，在左右图像上根据极线约束，对目标特征点进行搜索匹配获取目标的深度图像，并对深度图像进行优化、除噪声和去粗差，获得稳定可靠的目标三维点云并对物体空间分布进行限定，如图8所示。

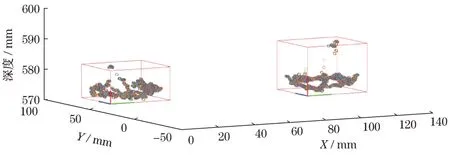
图8 物体空间分布Fig.8 Spatial distribution of objects

在优化后的物体特征点云中，随机采样5个特征点对其深度特征值进行统计并与真实值进行对比，结果如表1所示。

分析表1可知，获取的点云深度特征值与真实的特征值的平均误差为1.628 mm，可以满足任务要求。

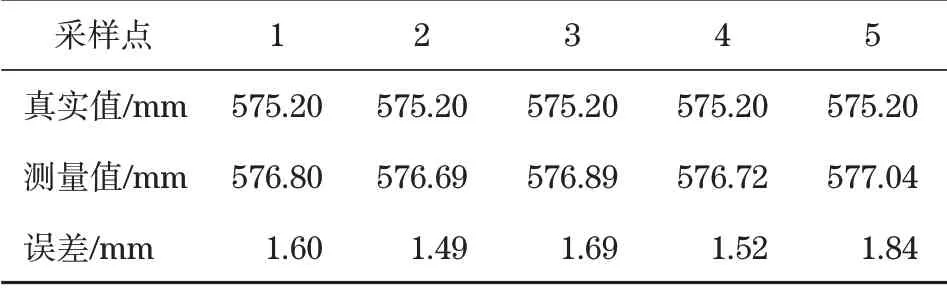
表1 特征点云深度统计Tab.1 Feature point cloud depth statistics

2.2 位姿估计与误差评估

对图像上的物体进行分割，并通过深度边缘检测获取位姿估计所需要的特征点，通过式（7）对每一个区域内的特征点进行计算评价，结果如图9所示。

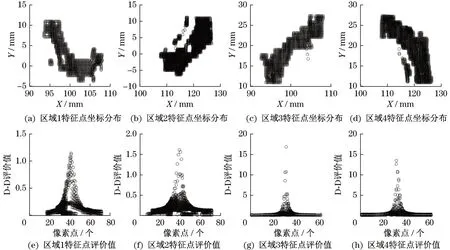
图9 区域特征点评价值Fig.9 Value of regional feature reviews

将最优得分特征点作为建立工件坐标系的特征点，建立的2个物体工件坐标系如图10和图11所示。

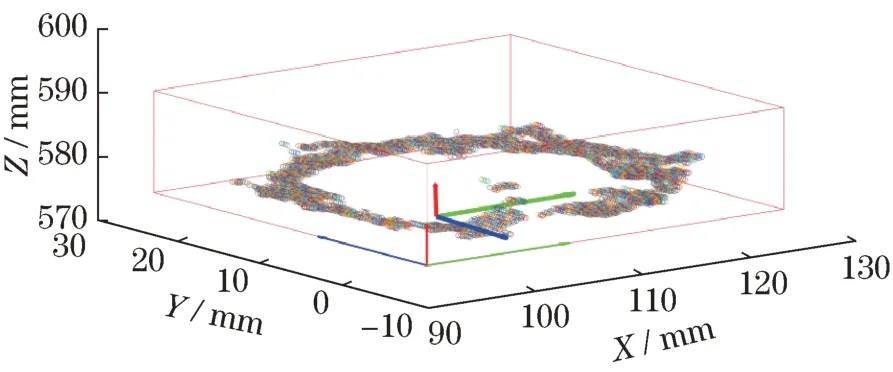
图10 目标1位姿Fig.10 Target 1 position

图11 目标2位姿Fig.11 Target 2 position

根据相机坐标系下的特征信息与对应的工件坐标信息的转换关系，获取工件坐标系与相机坐标系的转换关系R矩阵。同时根据式（18）～式（20）计算回转角γ、俯仰角β和偏转角α，计算结果如表2所示。

表2 3个坐标轴的夹角Tab.2 Angle of the three axes

分析获取的夹角数值，建立的工件1、2坐标系与实际坐标系的Z轴分别相差1.212°和1.503°，能够满足任务的要求。

为了验证所获取的相机坐标系与工件坐标系的位姿矩阵的准确性，这里针对相机坐标系与工件坐标系的转换误差进行分析。在点云集中随机采样20个点。通过相机坐标系和工件坐标系的几何关系求取特征点在工具坐标系下的三维坐标，同时根据所获得的位姿矩阵进行相同点的相机坐标系下与工件坐标系的转换，前后对比通过获得的转换矩阵获得的X、Y和Z位置信息误差进行验证，如图12所示。

图12 基于点云的X-Y-Z轴误差统计Fig.12 X-Y-Z axis error statistics based on point cloud

选择目标物体的4个定点计算其在相机坐标系下的坐标值，并根据4个定点建立工件坐标系获取相机与工件坐标系的转换矩阵M。对上述过程中的20个采样点进行坐标系转换获取X、Y和Z轴的误差，如图13所示。

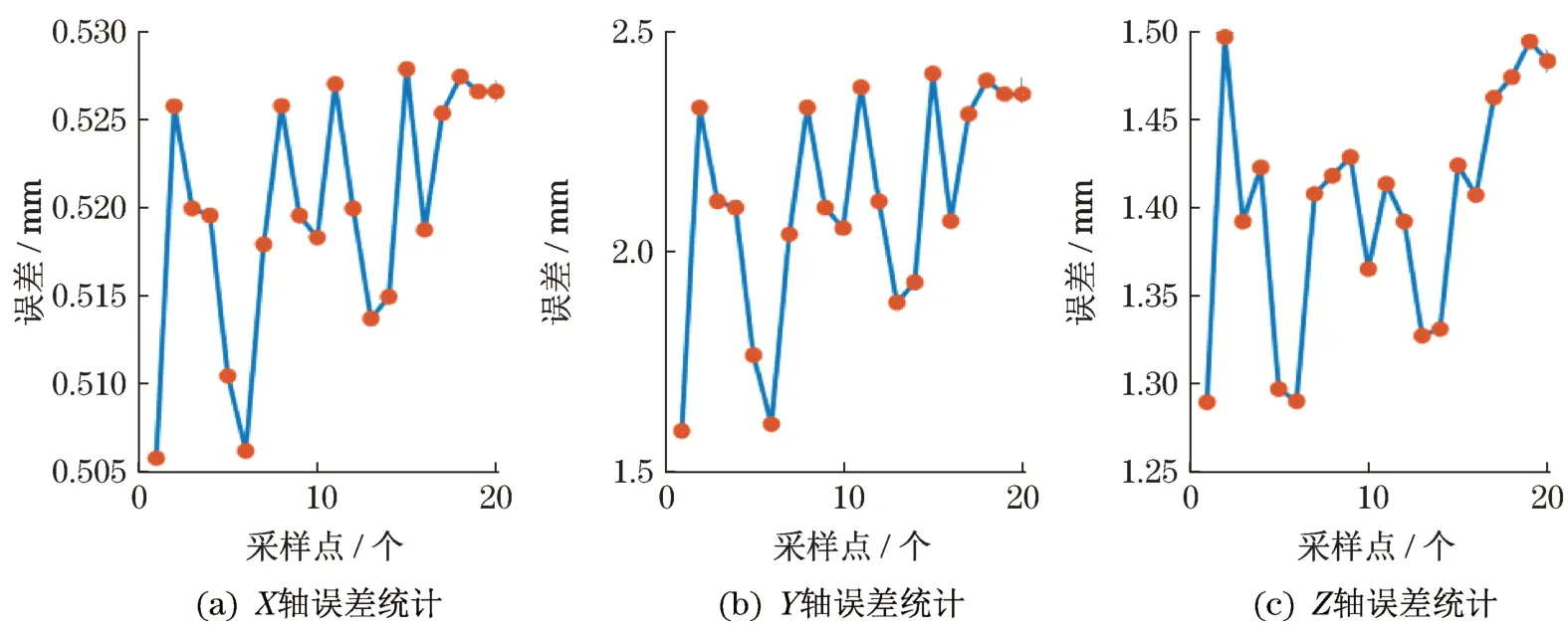
图13 基于选定点的X-Y-Z轴误差统计Fig.13 X-Y-Z axis error statistics based on selected points

统计20个采样点在2种方法下，3个轴上的误差如图14所示。

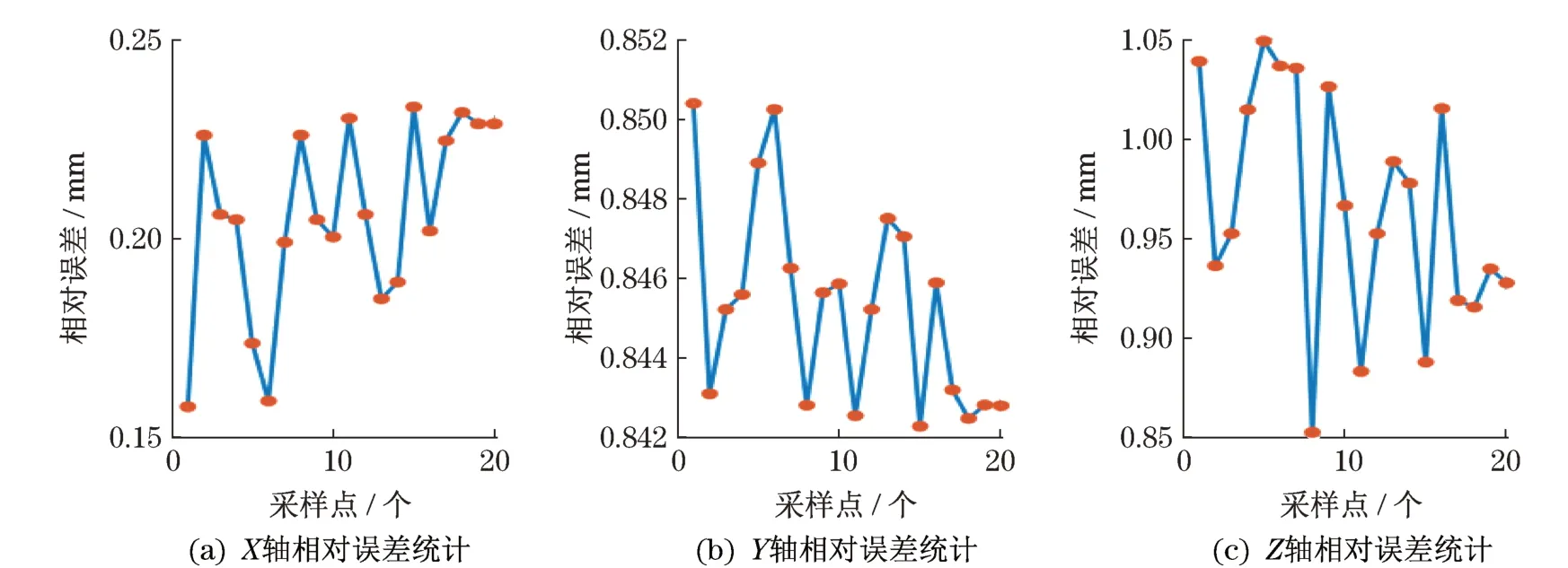
图14 X-Y-Z轴相对误差统计Fig.14 X-Y-Z axis relative error statistics

对比分析可知，在Y轴上本文方法比定点算法的平均误差低了0.75 mm，Z轴误差低了0.96 mm，X轴误差高了0.21 mm。分析采样点的误差结果可以看出，3个坐标轴的误差变化幅值差异较大，这是由于相机的径向畸变和切向畸变的变化速度不同引起的，且相机畸变校正不易完全还原，因此，深度方向的测量误差会引起整体误差增大。

3 结论

本文通过对点云区域估计获取了具有代表性的特征点，在双目立体匹配获取的误差基础上，根据特征点云能够获得稳定可靠且误差相对较小的位姿矩阵。通过实验分析获得以下结论：①采用背景差分法得到了图像中物体的位置并进行分割，获得噪声抑制的图像数据集，并采用图像立体匹配获得目标物体的三维点云，通过对点云进行优化和去粗差，可获得稳定可靠的物体点云信息。②在深度维度上对目标物体每一个特征点求取梯度，通过对梯度的分类可以获取到具有代表性的物体特征点。③根据区域点云评价函数可以得到建立工件坐标系需要的特征点，通过建立的工件坐标系，可以得到工件相对于相机的位姿矩阵。在3个坐标轴的平均误差和为2.43 mm，3个轴转角的平均误差为1.08°，验证了所提方法对结构规整的工件进行位姿计算时的可行性。