液压凿岩机器人机械臂轨迹规划研究

郭 锐，石 月，李永涛，覃艳明，赵静一

（1.燕山大学河北省重型机械流体动力传输与控制重点实验室，河北秦皇岛066004；2.浙江大学流体动力与机电系统国家重点实验室，浙江杭州310027；3.燕山大学先进锻压成形技术与科学教育部重点实验室，河北秦皇岛066004；4.燕山大学河北省特种运载装备重点实验室，河北秦皇岛066004）

工业机器人在日益信息化和自动化的工业背景下，已逐渐被应用到汽车、电子工业、建筑业、国防等各个领域。机械臂是工业机器人的重要执行机构，其轨迹规划的好坏会直接影响机器人作业的质量。因此，对机械臂关键技术的研究具有重要的现实意义［1-2］。机械臂运动轨迹规划是机械臂运动控制的基础和前提，也是减少机械臂磨损、节省工作时间、提高整体工作效率、促进机械臂高效和稳定运作的重要手段。近年来，学者们在机械臂的轨迹规划问题上做出了大量的实验与研究。Gregory等［3］对基于最优能耗的机械臂运动轨迹进行了大量的研究；Gasparetto等［4］重点研究分析了轨迹执行时间最优与轨迹光滑性最优的权重问题；马振书等［5］以排爆机械臂为研究对象，采用外加虚拟点法保证3次样条曲线可任意指定轨迹初始速度、加速度，用以提高机构灵活性。由于在动作起停点之间可以生成无数条满足运动条件的轨迹，所以在对机械臂进行轨迹规划时需要一些优化准则对生成的轨迹进行筛选，例如耗时最短、系统能耗最小、运动最平稳等［6］。

因此，针对液压凿岩机器人机械臂，在满足机械臂的运动学要求的同时考虑其质量、负载大小等多种因素，以机械臂平稳运行为优化原则在关节空间内对机械臂进行轨迹规划，并采用AMESim对机械臂液压系统进行运动轨迹跟踪仿真，以液压系统的耗能和系统功率为优化指标对轨迹进行分析，最后对液压凿岩机器人进行轨迹实验，证明所规划轨迹的合理性。

1 机械臂运动学模型

1.1 机械结构

此次研究的机械臂为8自由度机械臂，由6个转动副及2个移动副组成，三维模型如图1所示。液压系统为机械臂提供动力，各关节的运动依靠相应的液压缸来完成。

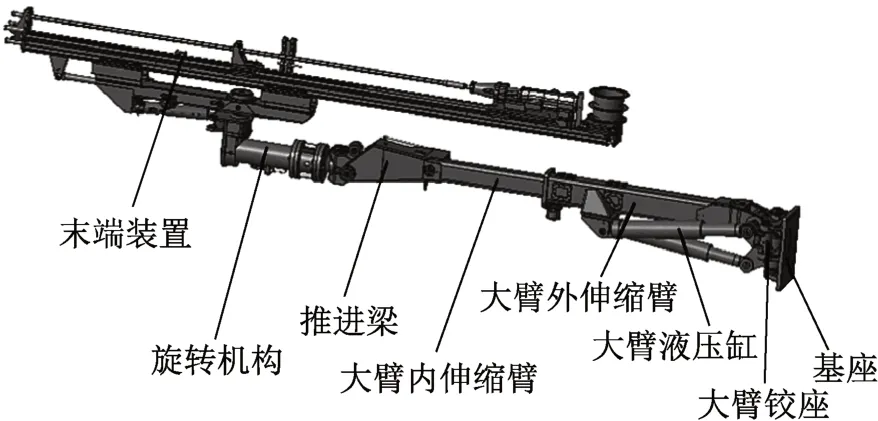
图1 液压凿岩机器人机械臂三维模型Fig.1 3D model of hydraulic rock-drilling robot manipulator

1.2 机械臂运动学模型

1.2.1 D-H参数确定

根据Denavit-Hartenberg参数法定义连杆坐标系。设x0y0z0为基座坐标系，xiyizi与机械臂第i个杆件固连。为了简化计算，设定关节1的坐标系为基础坐标系，之后依次建立各关节的相应坐标系，各关节坐标系如图2所示。

图2 机械臂各关节坐标系Fig.2 Coordinate system of each joint of the robot manipulator

根据各连杆参数以及所得坐标系之间的转换求得各关节的D-H参数，如表1所示。表中，ai-1为杆件长度，αi-1为扭转角，di为偏移距，θi为关节角。

表1 液压凿岩机器人机械臂的D-H参数Tab.1 D-H parameter s of hydraulic rock-dr illing robot manipulator

1.2.2 变换矩阵计算

由各关节对应坐标系以及D-H参数表可求得各连杆的齐次变换矩阵。相邻两坐标系的齐次变换矩阵可表示为

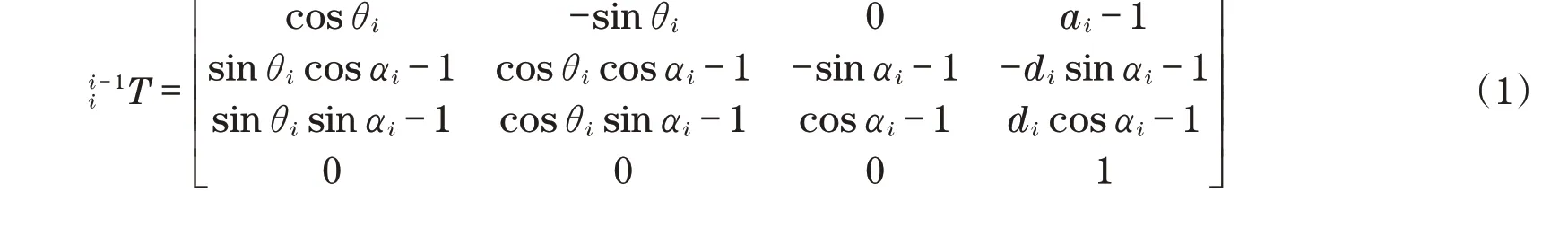
文献［9］对该液压凿岩机器人机械臂进行了各自由度的齐次变换矩阵，得到机械臂的末端位姿矩阵为

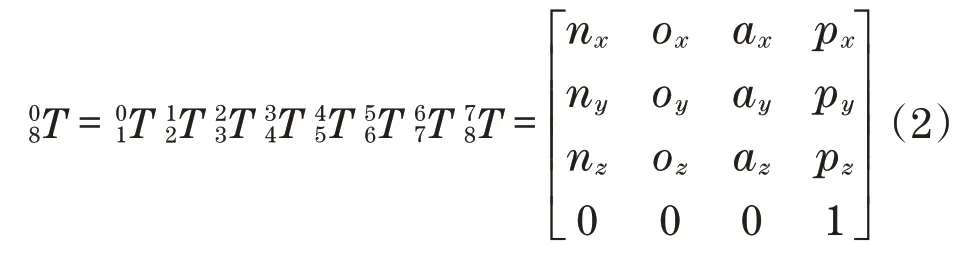
由式（2）进一步求得机械臂初始位姿矩阵为

根据所得到的运动方程，由位姿矩阵T求解方程即可求出机械臂的运动学逆解。根据所设定的约束条件在关节空间内使用关节角度的插值函数θ（t）来表示机械臂的运行轨迹，求解即可得到满足约束条件的光滑轨迹曲线［10］。

2 机械臂关节空间轨迹规划

对于工程机械用机器人来说，可以用来进行轨迹规划的空间主要有两种：关节空间和笛卡尔空间。笛卡尔空间内获取关节位姿、加速度等信息需要通过频繁转换坐标系的方法，计算量非常大，轨迹规划步骤非常复杂。相较而言，在关节空间中规划轨迹较为简便，并不存在机构奇异性问题。因此，考虑本次研究的机械臂的工作特点，选取关节空间来进行轨迹规划［11］。

2.1 五次多项式轨迹规划

五次多项式插值方程涉及6个约束条件，在三次多项式的基础上增加了对起始角速度和终止角速度的约束［10］。与三次多项式插值相比，五次多项式下轨迹的加速度较为平滑，不会出现跳变的情况。五次多项式插值下机械臂各关节的运动学参数可表示为

在初始时刻t0及终止时刻tf时，应满足的约束条件如下：

求得机械臂轨迹表达式的系数为

式中：c=θf-θ0。

将系数代入式（4），即可求得五次多项式插值下的机械臂位移函数θ(t)。

2.2 关节坐标空间的轨迹规划仿真

基于机械臂的运动学模型，利用Robotics Toolbox工具箱进行关节坐标空间的轨迹规划仿真。在关节空间进行规划时，需运用到jtraj函数的调用格式为

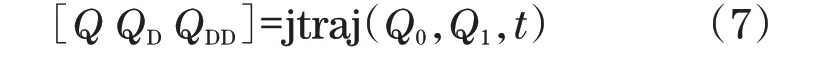
式中：Q0、Q1分别为机械臂的起始位置和终止位置；t为机械臂运动时间，此次规划设定运动时间为30 s；Q为机械臂的关节空间轨迹规划，它表达了从Q0向Q1状态转化过程；QD为关节速度；QDD为关节角加速度。

运用Robotics Toolbox工具箱进行逆运动学求解，得到机械臂各关节变量分别如图3、图4和图5所示。

jtraj函数调用代码为

由图3、图4和图5可以看出，机械臂8个关节的角位移、角速度和角加速度曲线均为光滑曲线。这表明机械臂沿该轨迹动作能减少各个运动参数的突变和运动冲击，降低机械振动，保证机械臂能够平稳、平滑地运行，确保足够的作业精度。

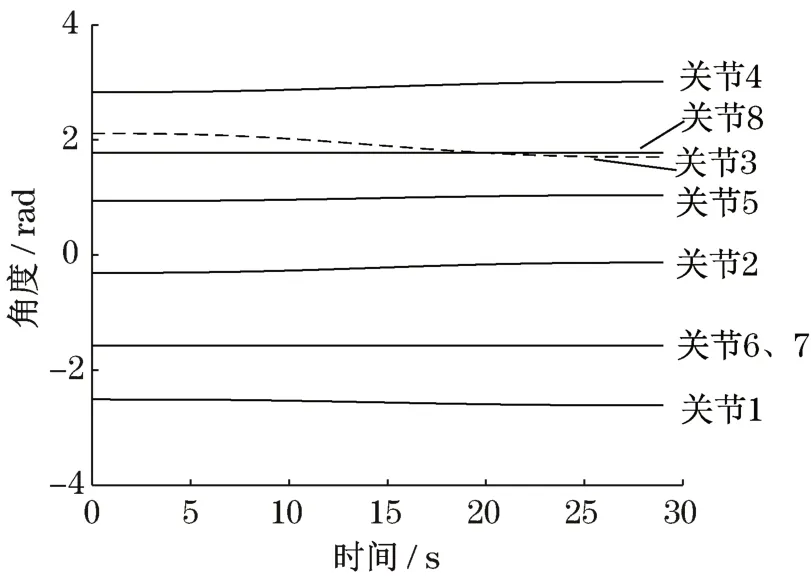
图3 五次多项式下轨迹变化曲线Fig.3 Trajectory curve under fifth degree polynomial

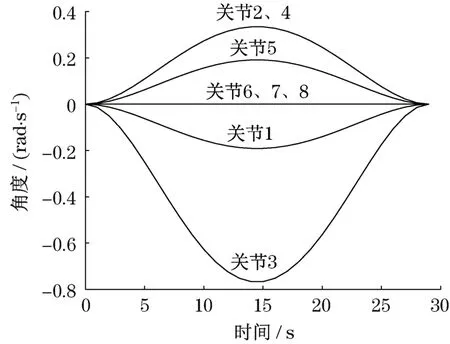
图4 各关节角速度变化曲线Fig.4 Angular velocity curve of each joint

图5 各关节角加速度变化曲线Fig.5 Change curve of acceleration of each joint

为了进一步研究五次多项式插值在液压凿岩机器人机械臂轨迹规划中的优越性，对机械臂在关节空间内运用三次多项式插值和带有抛物线过渡插值进行轨迹规划，并对3种插值方式下得到的运行轨迹进行液压动力系统建模仿真，对3条轨迹下液压系统提供动力时所涉及的耗油量和功率等变量进行对比分析。

3 基于AMESim的液压系统仿真

3.1 机械臂液压系统的AMESim建模

基于AMESim的机械臂液压系统模型如图6所示。模型分为液压系统和控制系统，液压系统采用Hydraulic模型库创建。液压缸末端放置位移传感器用来获取活塞杆的瞬时位移，并与输入信号共同作用控制各电比例阀开合情况，进而控制液压缸的伸缩。为了简化模型，采用PID控制来代替原液压系统中的平衡阀，避免活塞杆在伸缩过程中发生较大抖动，以保持运动的平稳性，提高位移精度，实现对各关节运动的精确控制，跟踪期望的运动轨迹［12］。

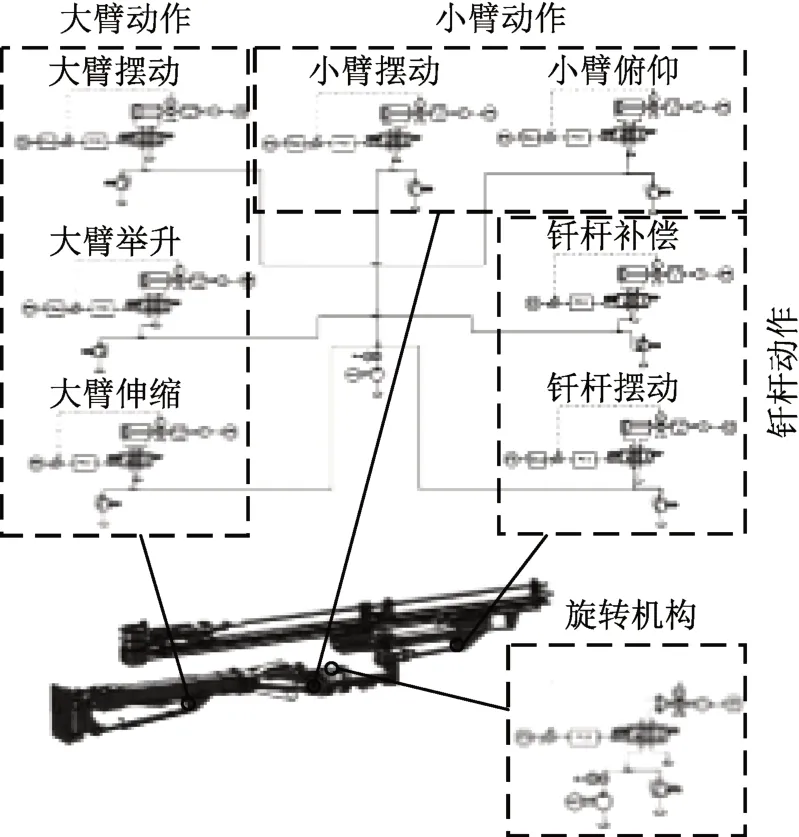
图6 机械臂液压系统模型图Fig.6 Mechanical arm hydraulic system model diagram

鉴于液压系统仿真的重点在于液压系统耗油量及功率等参数的获取，因此，在建模过程中省略对于机械臂机械结构的搭建，以质量块及输入力矩信号模拟机械臂运动时活塞杆的受力情况。为了明确机械臂沿给定轨迹运动时各关节所对应的控制信号，在ADAMS对机械臂进行动力学仿真，对液压缸的受力进行求解获取各液压缸端点处的受力及旋转惯量、关节角度变量等信息，并在线性化处理后将这些量作为输入信号输入到模型中。

3.2 仿真结果及分析

为验证机械模型精确程度，以仿真过程中机械臂末端液压缸的仿真位移与实际位移的偏差为参考。末端液压缸位移与位移偏差分别如图7、图8所示。

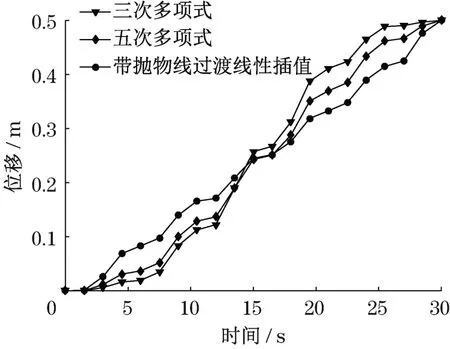
图7 机械臂末端轨迹曲线Fig.7 Trajectory curve of robot arm

图8中，机械臂末端点的给定轨迹与反馈轨迹偏差在2 mm以内，有较高的重合度，也符合机械臂的实际运动要求，说明所建模型有较高的精确性。通过仿真得到3种不同轨迹下的液压系统耗油量曲线与功率曲线如图9和图10所示。由图9及图10可看出，五次多项式下的轨迹在运动时的耗油量整体上处于中等的状态，消耗的功率最小，故无论是从平稳运行还是从节能的角度来选择，五次多项式的规划方法均能满足要求。

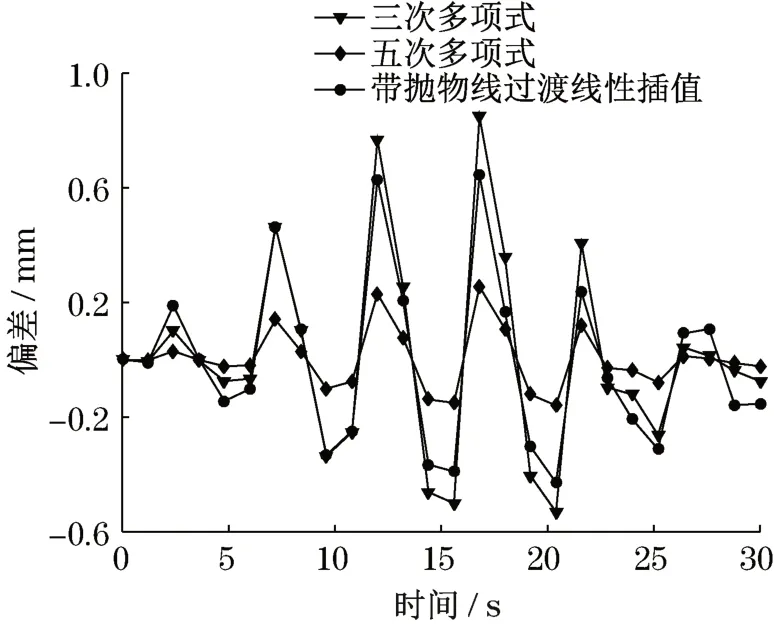
图8 末端轨迹位移偏差Fig.8 End joint track displacement deviation

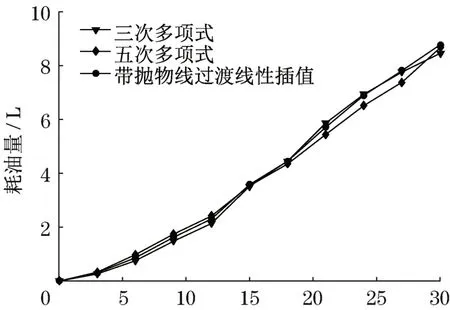
图9 液压系统耗油量曲线Fig.9 Fuel consumption curve of hydraulic system

图10 液压系统功率曲线Fig.10 Power curve of hydraulic system

4 机械臂轨迹实验

液压凿岩机器人机械臂轨迹实验平台主要由实验对象、液压系统、控制系统、测量系统等组成。实验过程中选取已投入使用的液压凿岩机器人机械臂为例，具体搭建平台如图11所示，机械臂与底座固连，正前方放置白色幕布并在幕布上标定机械臂末端所要到达的位置点，激光笔放置于机械臂末端用于人为追踪机械臂位置。

图11 液压凿岩机器人机械臂Fig.11 Manipulator of hydraulic rock-drilling robot

根据轨迹规划的路径，给定油缸的实际信号，实时通过传感器采集数据，得到输入轨迹与实际轨迹、末端油缸位移误差分别如图12和图13所示。由实验结果可知，在五次多项式插值规划的轨迹下，机械臂运动平滑且实际位置与理论位置偏差在直径2 cm范围内，精度上符合机械臂的工作要求，证明了该轨迹的合理性和可靠性。

图12 轨迹跟踪曲线Fig.12 Trajectory tracking curve

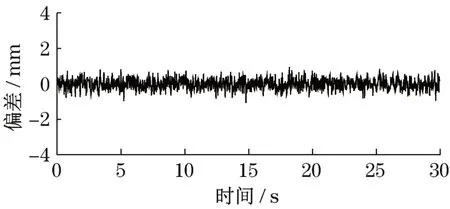
图13 位置误差曲线Fig.13 Position error curve

5 结语

以液压凿岩机器人机械臂为研究对象，构建机械臂运动学模型，通过五次多项式插值算法在关节空间内对机械臂进行轨迹规划，在此基础上对机械臂液压系统进行建模仿真。以机械臂的平稳运行和能耗为优化指标，对比分析五次多项式插值法、三次多项式插值法和带抛物线过渡的线性插值在机械臂轨迹规划中的特点。仿真结果表明，运用五次多项式规划的轨迹，无论是在运动平稳性上还是节能性上，均优于其他两种插值方法下的轨迹。最后对液压凿岩机器人进行了轨迹实验，验证了所规划轨迹的正确性和有效性。