水电站地下埋管回填脱空影响计算分析

申 艳，冯浩文，黄永松

（华北电力大学，北京102206）

0 引 言

地下埋管深埋于地层岩石之中，通过铺设地下埋管，可以缩短压力管道的长度，省去支撑机构。地下埋管与围岩联合承载可以减小钢衬厚度、节约钢材，同时受外界条件影响较小，因此在大中型水电站中被广泛应用［1，2］。地下埋管在施工中需要回填混凝土，通过灌注水泥浆（或水泥砂浆）并形成结石，用以充填钢管与混凝土之间的空隙，使外围混凝土（及地下埋管的围岩）与钢管能够共同承受内水压力［3］。

钢衬回填混凝土作为维持结构稳定性和安全性的一道必备工序，经过多年实践发展，已形成相对固定的施工程序［4］。我国多采用先钻孔、再灌浆，最后补孔的传统工艺，近年来兴起使用FUKO管等新兴工艺［5］进行灌浆。在首次回填混凝土浇注完成之后，经过长时间的运行，由于混凝土与钢管两种材质接触不紧密，以及受施工过程中荷载变化、混凝土凝固收缩、变形不一致以及温度、施工工艺等因素影响，易产生脱空现象。脱空现象使得钢管单独承担内压，进而造成钢管的应力恶化以及不均匀变形，严重时还可能造成钢管的破损，严重威胁整体结构的安全性。如1999年投产发电的云贵响水电站由于钢管底部混凝土浇筑质量较差，导致混凝土与钢管之间脱空缝隙值过大，无法保证钢衬、混凝土和围岩之间的联合受力，最终导致建成运行不久便发生了失稳。

水电站地下埋管回填脱空的分布范围及深度，是工程是否需要进行补充灌浆的重要参考依据。工程实际中往往需要对脱空区域进行探测并重复灌浆，直至满足设计要求。目前常用的探测方法包括灌浆孔探测、锤击探测［3］和以中子无损探测为代表的无损探测等［6，7］。《水工建筑物水泥灌浆施工技术规范》［8，9］规定：隧洞钢衬面积大于0.5 m2的脱空区宜进行接触灌浆。非高强钢通常采用钢板预留灌浆孔的方式进行接触灌浆［10］，高强钢通常采用预埋灌浆管进行接触灌浆。然而在实际接触灌浆实施之后，钢管与混凝土之间仍然存在超出规范允许值的脱空部位。压力钢管回填脱空，会造成脱空部位钢衬应力集中［11，12］；当脱空面积较大时，钢衬应力甚至会超过材料的抗力限值，对工程造成较大的安全隐患。

本文以某电站压力钢管接触灌浆的实际为例，采用有限单元法，建立切合实际情况的有限元模型，对钢管底部混凝土脱空范围及缝隙宽度等进行敏感性分析。通过对比材料的抗力限值，给出允许的脱空范围和允许的脱空深度，并对接触灌浆质量合格标准的确定给出了指导性意见。图1为该工程压力钢管上平段底部脱空区分布图。

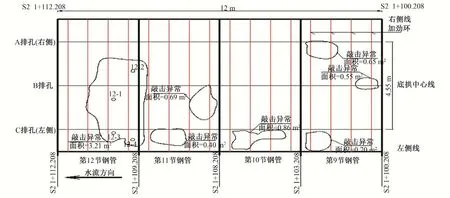
图1 某工程压力钢管上平段底部脱空区分布图Fig.1 Distribution map of the empty area at the bottom of the upper flat section of a penstock

1 有限元计算模型

1.1 埋管模型简化与假定

为了使地下埋管有限元模型不至太过复杂，本文对围岩及回填混凝土进行了合理的简化，采用的基本假定有：①围岩为均质各向同性，且应力状态处于线弹性范围以内；②支护工程已经完成，埋管不承担山岩压力；③在内水压力作用下，混凝土径向均匀开裂，钢衬所承受的内水压力部分通过径向开裂后的回填混凝土传递到岩石上，回填的素混凝土只起传递荷载作用；④地下埋管钢衬、混凝土、岩石之间的缝隙值包括施工缝隙、钢管冷缩缝隙和围岩冷缩缝隙。将混凝土与钢管之间的缝隙及混凝土与围岩之间的几种缝隙合并为一层缝隙，根据钢管的直径和温度资料确定管壁外法线方向的缝隙值。当缝隙值大到一定程度，就产生脱空效应，文章中计算所采用的脱空深度包括了正常缝隙值；⑤围岩只对钢管管壁的法向位移起弹性约束作用，将这种作用简化为具有法向刚度的K0接触单元，即作用在围岩上的径向力满足P=K0⋅δ的条件，δ为围岩的径向位移。

1.2 单元的选取

钢管采用ANSYS 中4 节点板壳单元进行模拟，加劲环采用带有截面形状的三维梁单元进行模拟［13］。回填混凝土开裂后只起传递荷载的作用，这里将其与围岩作为一个整体处理，将其简化成只对管壁正法向位移起弹性约束作用的“弹性连杆”，用ANSYS 中能够考虑缝隙值的点点接触单元来模拟。当钢管变形值小于缝隙值时，围岩不起作用；当钢管某处变形值达到并超过缝隙值时，该处围岩相当于受压的弹性刚度为K0的“弹性连杆”，“弹性连杆”靠近钢衬的一端随管壁一同变形，同时对管壁作用有径向反力。通过上述单元选取及模型简化与假定，就可以模拟钢管和围岩联合承担内水压力。

1.3 钢衬与围岩联合作用计算模型的验证

为了验证模型简化和单元选择的合理性，采用此模型和单元模拟具有解析解的圆管段，并将有限元计算结果与解析解进行对比分析。

（1）算例计算参数。压力钢管的半径2.4 m，壁厚58 mm，计算壁厚56 mm，内水压力8.0 MPa，初拟缝隙值Δ=1.2 mm，钢材弹性模量Es=2.06×105N/m2，围岩单位弹性抗力K0=1.0 N/mm3。

（2）解析解。地下埋管环向应力σθ按下式计算：

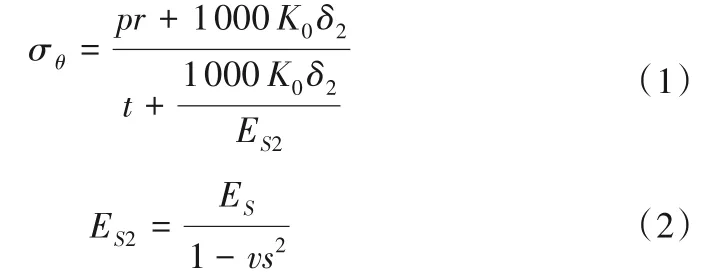
式中：p为内水压力设计值，N/mm2；r为钢管内半径，mm；K0为岩石单位抗力系数（较小值），相应于岩石变形模量，N/mm3；ES2为钢材平面应变问题的弹性模量，N/mm2；ES为钢材的弹性模量，N/mm2；vs为钢材的泊松比。

根据解析公式可知，该管段钢衬不考虑围岩分担时，环向应力的解析解为343 MPa，考虑围岩分担时，环向应力的解析解为302 MPa。

（3）有限元模型的建立。根据算例，管壳采用ANSYS 软件中的4 节点壳单元，单元网格宽度24 cm，采用考虑缝隙的点点接触单元模拟围岩作用。

（4）有限元计算结果与解析解的对比分析。有限元计算结果显示，该管段钢衬不考虑围岩分担时，环向应力为342 MPa；考虑围岩分担时，环向应力为305 MPa。对比分析有限元计算结果与解析解发现，有限元的计算结果与解析解十分接近。不考虑围岩分担时，计算误差不超过0.3%；考虑围岩分担时，计算误差不超过1.3%。可见，当采用4 节点壳单元模拟管壳，采用点点接触单元模拟围岩的作用时，该有限元模型能够较好地反映地下埋管的受力状况，计算精度能够满足工程要求。

2 回填脱空区的边长效应

实际工程中，同样的脱空面积，有的脱空区管道轴线方向长度和管道弧长方向长度接近，有的脱空区管道轴线方向长度和管道弧长方向长度相差较大。同样的脱空面积，由于边长不同，可能会对钢衬的受力产生不同的影响。

为分析管道回填脱空影响的边长效应，以该电站中平段为例，建立了3 个对比分析模型。这3 个模型的几何尺寸、材料、围岩参数、荷载等计算参数相同，脱空面积也相同。具体来说，管道直径均为5.8 m，设计内水压力均为3.78 MPa，均采用07MnMoVR钢衬，钢衬厚度均为40 mm，围岩单位弹性抗力系数均为3 kN/cm3，管道缝隙值均为1.2 mm；脱空面积均为1.05 m2。3 个模型的区别在于脱空区的边长不同，模型1 脱空区的管道弧长方向和管道轴线方向长度接近；模型2 脱空区的管道轴线方向长度约为管道弧长方向的4 倍；模型3 脱空区的管道弧长方向长度约为管道轴线方向的4倍。

本文整理了脱空区表面最大Mises 应力、中面最大Mises 应力、最大径向位移，并将钢衬应力与材料的抗力限值进行了对比分析，见表1，这3 个方案的应力云图和位移云图见图2～图5所示。

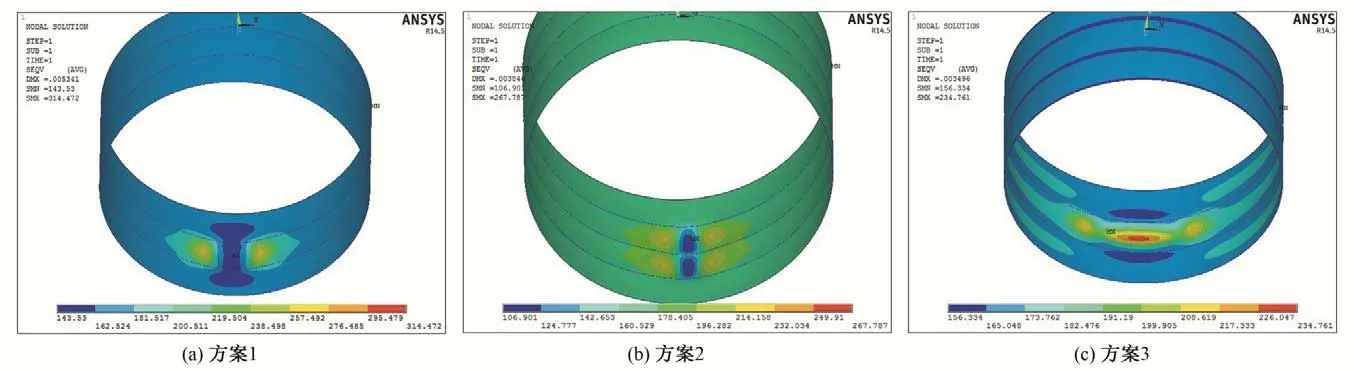
图2 脱空区内表面Mises应力云图（单位：MPa）Fig.2 Mises stress cloud diagram of the surface in the empty area

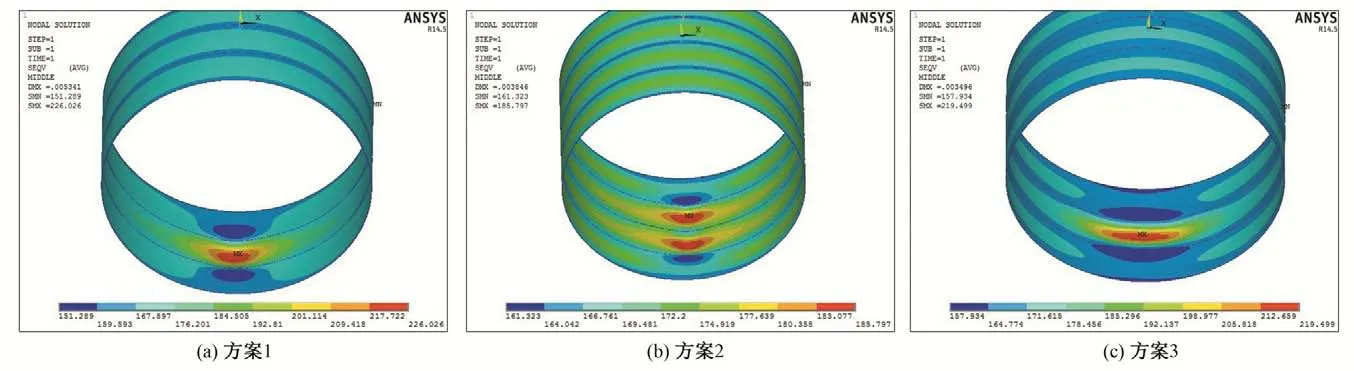
图3 脱空区中面Mises应力云图（单位：MPa）Fig.3 Mises stress cloud diagram in the middle of the empty area

图4 脱空区外表面Mises应力云图（单位：MPa）Fig.4 Mises stress cloud diagram on the outer surface of the empty area

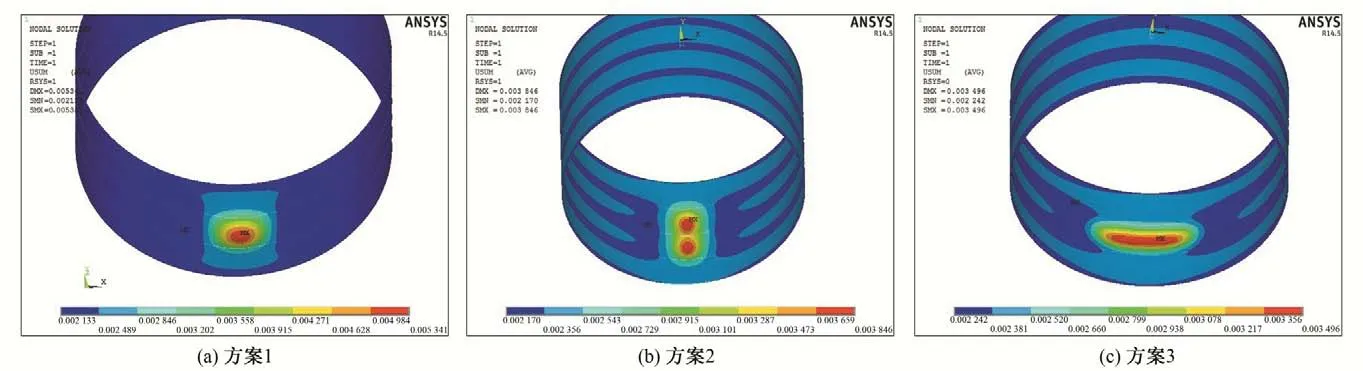
图5 脱空区位移云图（单位：m）Fig.5 Displacement cloud map of the empty area

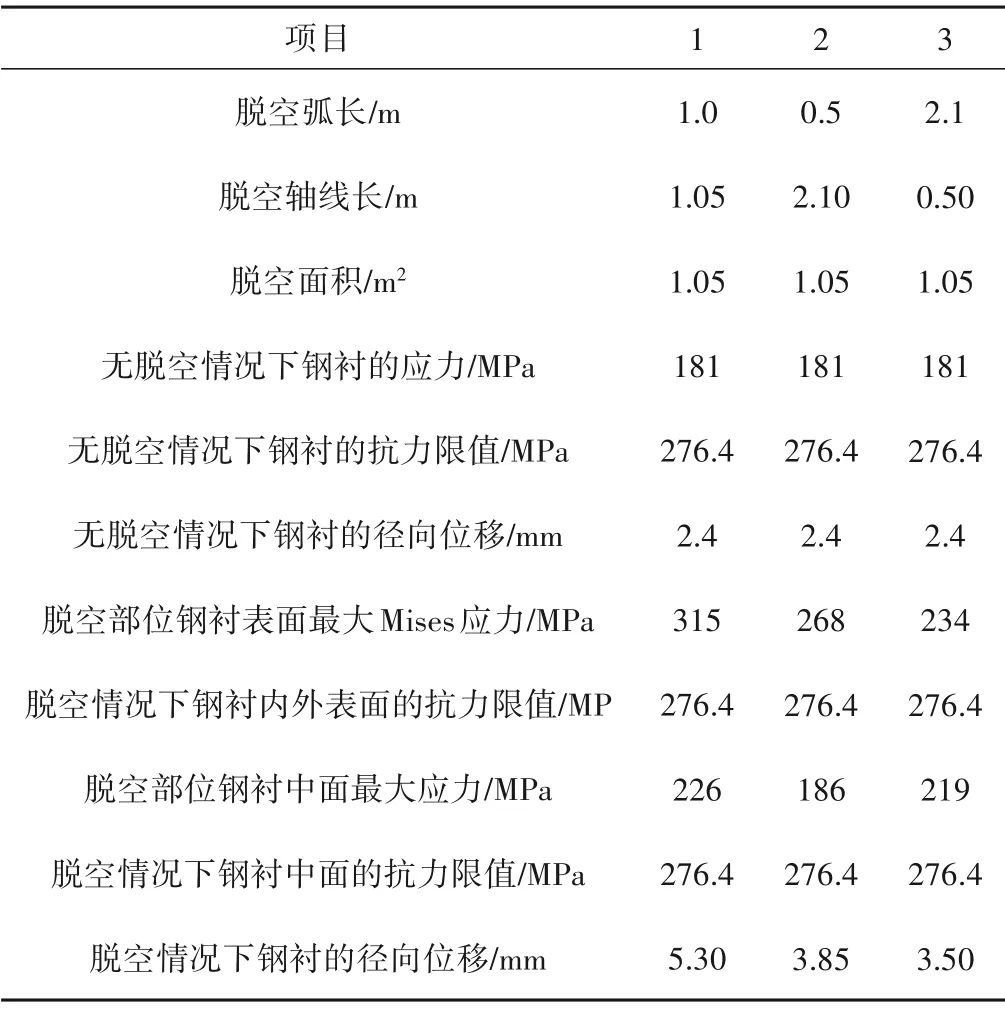
表1 脱空边长效应分析计算参数及计算结果Tab.1 Calculation parameters and calculation results for the analysis of empty side length effect

对比3个计算方案的计算结果可知：脱空面积相同，脱空弧长和脱空轴线长不同，应力升高和最大径向位移值也不尽相同。从计算结果来看，弧长和轴线长两个方向尺寸越接近，对钢衬受力越不利，应力和位移升高就越大。该规律也符合单向板、双向板的受力特性，即当区格板的长边与短边之比超过一定数值时，荷载主要通过沿板的短边方向的弯曲作用传递，沿长边方向传递的荷载可以忽略不计。

3 计算结果及分析

3.1 脱空范围敏感性分析

本文选取该电站引水钢管上平段（Ⅲ类围岩）、引水钢管上平段（Ⅳ类围岩）、引水钢管中平段（Ⅲ类围岩）、引水钢管中平段（Ⅳ类围岩）、引水钢管下平段和尾水支管的典型部位，假定该部位完全脱空，并进行了脱空范围的敏感性分析。选取的脱空面积分别为0.05、0.1、0.25、0.5、1.0、1.5、2.0、3.0、4、5.0 m2。根据第2 节的分析结论，假定脱空区弧长和轴线长基本相当。6个方案的计算参数见表2。本文整理了脱空区表面Mises 应力最大值、中面Mises 应力最大值、径向位移最大值相对脱空面积的敏感性变化曲线，见图6、7。

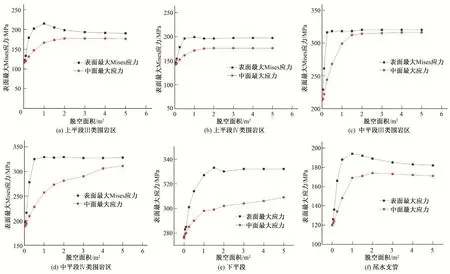
图6 钢管Mises应力最大值随脱空面积的变化曲线Fig.6 The change curve of the maximum Mises stress of steel pipe with the empty area

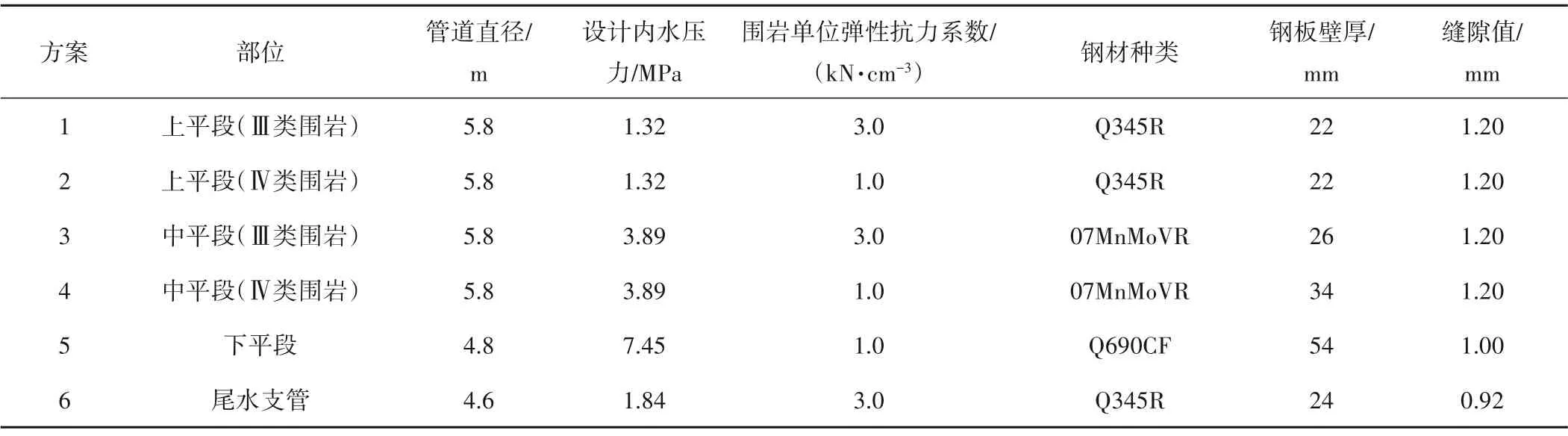
表2 脱空范围敏感性分析计算参数表Tab.2 Calculation parameter table for sensitivity analysis of empty range

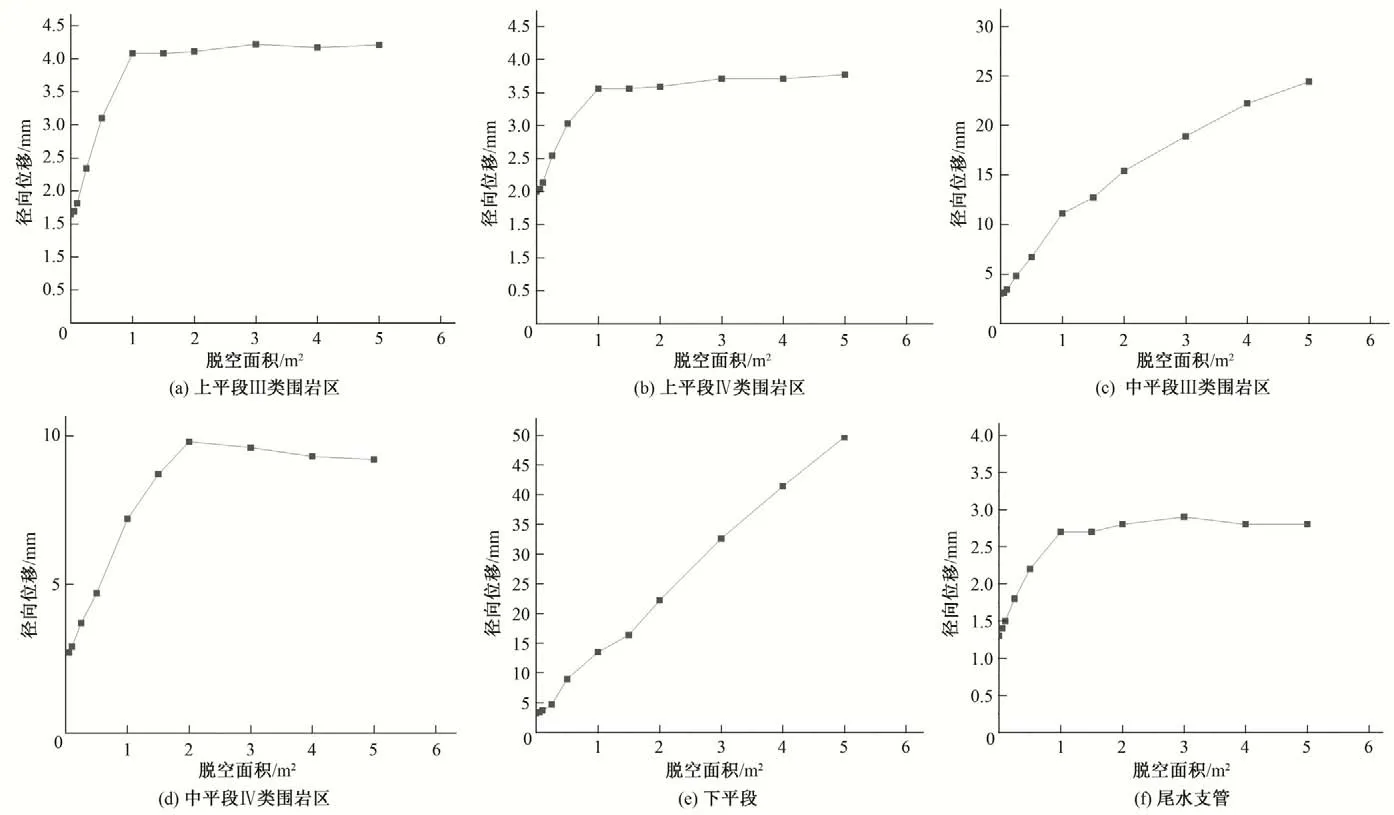
图7 钢管径向位移最大值随脱空面积的变化曲线Fig.7 Variation curve of maximum radial displacement of steel pipe with empty area

3.2 脱空深度敏感性分析

本文对该电站引水钢管上平段（Ⅲ类围岩）、引水钢管上平段（Ⅳ类围岩）、引水钢管中平段（Ⅲ类围岩）、引水钢管中平段（Ⅳ类围岩）、引水钢管下平段、尾水支管选取典型部位，假定该部位没有完全脱空且脱空面积不变，进行了脱空缝隙值的敏感性分析。选取的脱空缝隙值分别为1.0、1.5、2.0、2.5、3.0、3.5、4.0、4.5、5.0 mm、完全脱空。六个方案的计算参数见表3。本文整理了脱空区表面Mises 应力最大值、中面Mises 应力最大值、径向位移最大值相对脱空面积的敏感性变化曲线，见图8、图9。

表3 脱空深度敏感性分析计算参数表Tab.3 Calculation parameter table for sensitivity analysis of empty depth

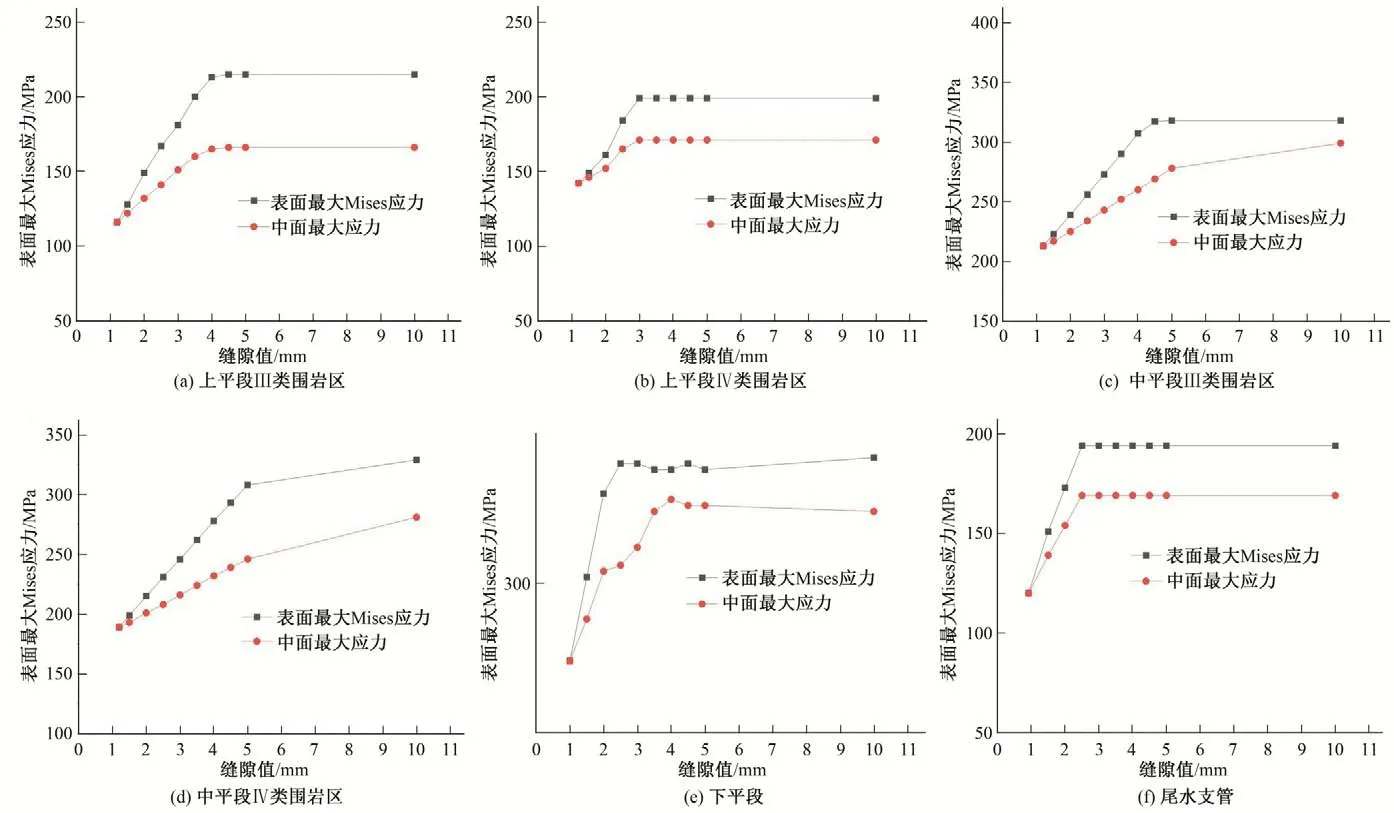
图8 钢管Mises应力最大值随缝隙值的变化曲线Fig.8 The variation curve of the maximum Mises stress of steel pipe with the gap value

图9 钢管径向位移最大值随缝隙值的变化曲线Fig.9 Variation curve of maximum radial displacement of steel pipe with gap value

4 结 论

通过对该水电站地下埋管回填脱空范围及深度敏感性计算分析，得到如下结论。

（1）通过对不同部位灌浆脱空范围敏感性分析可知：一般而言，脱空部位的应力最大值及位移最大值并不是随着脱空面积增加而不断增加；在一定的范围内，脱空部位的应力最大值及位移最大值随着脱空面积增加而增加，增加速率由快变慢；当脱空面积超过这个范围，脱空部位的表面应力及位移随着脱空面积增加变化不大。上平段Ⅲ类围岩区当脱空面积超过1.0 m2时，中平段Ⅲ类围岩区当脱空面积超过0.25 m2时，Mises应力最大值超过了材料的抗力限值，需要对该脱空部位进行补充灌浆。

（2）通过对各部位钢管典型断面脱空深度敏感性分析可知：一般而言，针对某一特定的区域，脱空部位的应力最大值及位移随着缝隙值的增加而增加；当缝隙值超过一定范围时，状态接近完全脱空，脱空部位的应力最大值及位移随着缝隙值的增加而基本不变。上平段Ⅲ类围岩区，脱空范围为1 m2时，当缝隙值超过4 mm，钢材的表面应力就会超过材料的抗力限值。中平段Ⅲ类围岩区，脱空范围为2 m2，缝隙值超过3 mm时，表面应力将超过材料的抗力限值。

（3）灌浆脱空对钢管的受力特性影响较大，应采取必要的措施尽量减少灌浆脱空的范围和缝隙值。由于不同管段的围岩弹性抗力、管径大小、荷载、钢材材料、设计富裕量等都不尽相同，要想回答各部位钢管允许脱空的范围，或者各部位钢管允许的缝隙值，不能一概而论，应该通过数值计算具体分析。《水工建筑物水泥灌浆施工技术规范》规定的，隧洞钢衬面积大于0.5 m2的脱空区宜进行接触灌浆，此条规定还是过于笼统。□