基于非线性多尺度模型的黄河三角洲降水量预测

穆玉珠，王燕鹏，张凤华，乔冬梅

基于非线性多尺度模型的黄河三角洲降水量预测

穆玉珠1，王燕鹏1，张凤华1，乔冬梅2*

（1.河南省新乡水文水资源勘测局，河南 新乡 453000；2.中国农业科学院 农田灌溉研究所，河南 新乡 453002）

【】提高降水量的预测精度，反映降水量的实际特征。基于经验模态分解对非线性时间序列的分析和处理的优势，对黄河三角洲气象站点1954—2018年连续65a月均降水量数据进行经验模态分解（Empirical Mode Decomposition, EMD），得到了系列本征模态函数(Intrinsic Mode Function，IMF)，对IMF进行Hilbert变换，在此基础上建立了2种黄河三角洲降水量多尺度预报模型。黄河三角洲降水量存在着9、13、23、76、135月左右的周期，并以9个月的波动为主；65 a月均降水量数据预测结果显示：模型一的相对误差在0.9%～9.8%之间，模型二的相对误差在1.6%～11.8%之间，在建模时不考虑初相位的模型一平均预测误差为2.70%，整体预测精度要优于考虑初相位的模型二。2种模型的拟合精度及显著性均符合要求。

降水量；时间序列；多尺度；EMD；预测

0 引言

【研究意义】在气候变化和人类活动双重因素的影响下，各地区的降水量也发生了变化[1-3]，降水与人类生产、生活及生态息息相关，降水量的变化关系到区域水资源的可持续利用、生态环境的保护与经济社会的发展，降水量的变化特征与演变趋势研究已成为水资源领域研究的热点，相关学者和研究人员都非常关注降水量的精确预测[3-4]。【研究进展】国内外针对降水量的预测主要为概率统计法和时间序列分析法[5-7]。付明明[8]运用ARIMA模型对新疆喀什地区的降水量进行预测，利用喀什地区2个子流域1950—2015年实测年降水量数据分析其模型的适用性和预测精度，模拟降水量和实测降水量之间的误差相对值低于20%。降雨时间序列往往随着时间呈现一定的周期性趋势，这种现象受多种随机因素的影响和制约，导致周期性趋势的偏离、跳跃和摆动，使得降水量存在一定的随机性和非平稳性。杨沛羽等[9]基于超阈值（POT）的极端降水事件抽样、变异分析、趋势分析等方法对黄河流域77个气象站点1957—2014年日降水数据进行分析，结果表明黄河流域极端降水量存在显著的非平稳性。概率统计无法适应数据的随机性和不平稳性，传统的时间序列法常常对数据自身的平稳性要求较高。也有部分学者采用多种方法对降水量非线性时间序列进行建模和预测[10-11]，何慧等[12]应用PCA-BP神经网络模型、遗传算法优化神经网络、RBF神经网络预测模型、小波神经网络模型、粒子群神经网络模型等对广西月降水量预测，得到较好的应用效果。但降水量时间序列是非线性、非稳定的和多尺度的，这些变化有月、年和代等多种，其演变特征是由很多错综复杂因素共同作用的结果，上述方法并未在本质上降低时间序列的非平稳性。20世纪90年代末，Huang等[13]、任博等[14]提出了一种时间序列分析方法经验模态分解（Empirical Mode Decomposition，EMD），该方法是一种基于时间序列局部特征的分解方法，EMD适用于对非线性、非稳定过程的复杂数据进行线性化和平稳化处理，其将复杂的时间序列分解为有限的、少量的固有模态函数（Intrinsic Mode Function，IMF）。通过对这些IMF进行Hilbert变换，得到各IMF的时变振幅和频率，能够准确地用波内调制机制反映出系统的非线性特性，这也是经验模态分解的另一优点，因此，可以有效提高降水量的预测精度。【切入点】目前主流的研究方法多为单一尺度的，无法反映降水量实际特征。小波分析虽然作为常用的多尺度分析方法，但是它的不足之处是存在较多噪点干扰，数据分辨率一般，缺少从降低时间序列非平稳性和多尺度层面的降水量预测方法研究。【拟解决的关键问题】研究通过对黄河三角洲1954－2018年月降水量的EMD分解，得到IMF固有模态函数，并对IMF进行Hilbert变换分析，得到相应的瞬时频率和振幅，分别建立针对研究区域的是否考虑初相位的2种降水量的多尺度数学模型，为黄河流域降水量的定量研究、水资源的利用及河口治理提供科学依据。

1 材料与方法

1.1 研究区概况与资料来源

黄河三角洲是指黄河入海口携带泥沙在渤海凹陷处沉积形成的冲积平原，该区域以山东省东营市利津县为顶点，北邻吐海河口，南邻小青河口，面积5 450 km2，其中东营市境内面积5 200 km2。黄河三角洲属暖温带半湿润大陆性季风气候区，冬寒夏热，四季分明，多年平均气温为11.7～12.6 ℃，年平均日照时间为2 590～2 830 h，无霜期211 d，年均降水量530～630 mm。三角洲顶部和中部海拔10 m以下的土壤脱盐较好，为农业主产区，海拔4 m以下沿海低地地下水位高，土壤盐碱化强，大部分仍是荒地。

研究所需资料来源于黄河三角洲气象站点1954－2018年连续65 a实测资料，在降水量数据处理时，部分年份缺测资料利用相邻站点采用相关分析进行插补。

1.2 研究方法

1.2.1 经验模态分解

EMD算法适合于分析非线性平稳信号，可以根据信号本身的特点提取信号的本征模函数，该算法不同于传统的基于线性稳定假设的傅立叶变换和小波变换，是一种新型的自适应信号时频分析方法。

EMD算法分解的IMF分量应满足2个条件：第一个条件是这些分量的最大值、最小值和零交叉数必须相等或最多有一个差；第二个条件是由最大值和最小值确定的上下包络的平均值在任何时间都为0。分解步骤如下：

1）寻找时间序列（）的局部极大值和极小值，极大值形成的上包络为（）、极小值形成的下包络为()，上下包络的均值()=[()+()]/2。

2）设1()=()-()，检验1()是否满足IMF的2个条件，如果满足1()就是IMF，如果不满足，对1()重复1），直至得到k()满足IMF的2个条件，k()就是第一个IMF分量，1()。记序列的剩余部分为1()=()-1()。

3）对1()重复1）和2），直至剩余部分为一单调序列，分解结束。通常情况下，IMF停止的标准是前后2个()的标准差，即：

当为0.2～0.3时IMF有较好的稳定性，同时可以使IMF的物理意义更加清晰。

1.2.2 Hilbert变换

对所有分解出的IMF进行Hilbert变换，C()的Hilbert定义如下：

式中：是柯西主值，根据（2）式，()与()形成复共轭，得到一个解析信号()：

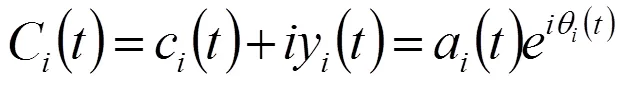
()为瞬时振幅，()为相位，即：

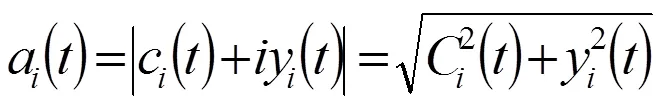
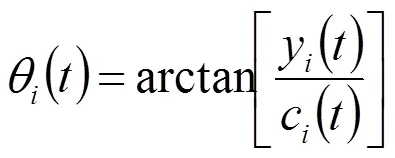
相应的瞬时频率为：

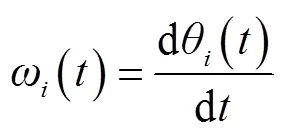
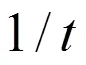
1.2.3 多尺度预测模型

1）模型一

根据EMD和Hilbert变换的结果，不考虑各IMF初相位的情况下建立如下模型：

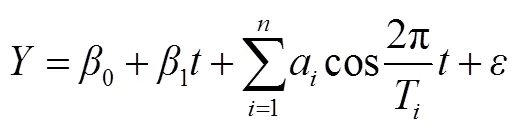
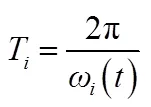
2）模型二

考虑IMF的初相位，建立如下模型:

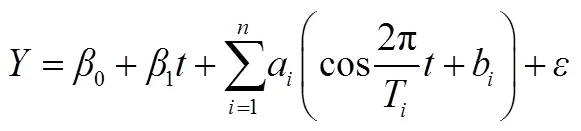
式中：表示各IMF分量的初相位，其余参数与模型一的意义相同。

2 结果与分析

2.1 EMD分解结果

对黄河三角洲气象站点1954－2018年连续65 a月平均降水量数据，进行EMD分解，得出6个IMF分量和1个残余分量（图1），每个IMF分量代表1个尺度上的波动变化特性。由图1可以看出，IMF1表达了降水量序列最高频波动的信息，从IMF1到IMF6，振幅逐渐减小，频率变低；其中残差项是单调的，体现序列的趋势，即降水量有上升的趋势。

2.2 Hilbert变换的统计值

对每个IMF组件执行Hilbert变换，以获取每个组件的平均幅度和平均频率，如表1所示。IMF1具有最高振幅，并且包含最高频率的振动信息。这表明研究所用时间序列的年降水量的时间序列振荡期约为9月。IMF1－IMF6的振幅逐渐减小，频率减小。除了9个月左右的周期外，还有13、15、23、76和135个月左右的周期。

表1 年降水量各分量统计值

2.3 模型参数的确定

模型一不考虑初相位，各项参数为：IMF1平均周期8.8，平均振幅1.71；IMF2平均周期12.9，平均振幅1.92；IMF3平均周期15.1，平均振幅1.55；IMF4平均周期22.7，平均振幅0.58；IMF5平均周期76.3，平均振幅0.72；IMF6平均周期135.2，平均振幅0.64（表1），代入式（7），建立的降水量多尺度模型为：

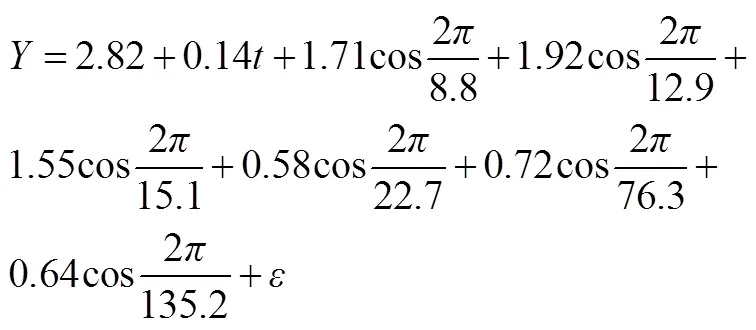
模型二较模型一考虑到各IMF分项的初始相位，根据表1数据可得各项参数为：IMF1平均周期8.8，平均振幅1.71，初相-1.21；IMF2平均周期12.9，平均振幅1.92，初相-0.62；IMF3平均周期15.1，平均振幅1.55，初相-0.38；IMF4平均周期22.7，平均振幅0.58，初相0.20；IMF5平均周期76.3，平均振幅0.72，初相1.19；IMF6平均周期135.2，平均振幅0.64，初相1.53，建立的降水量多尺度模型为：

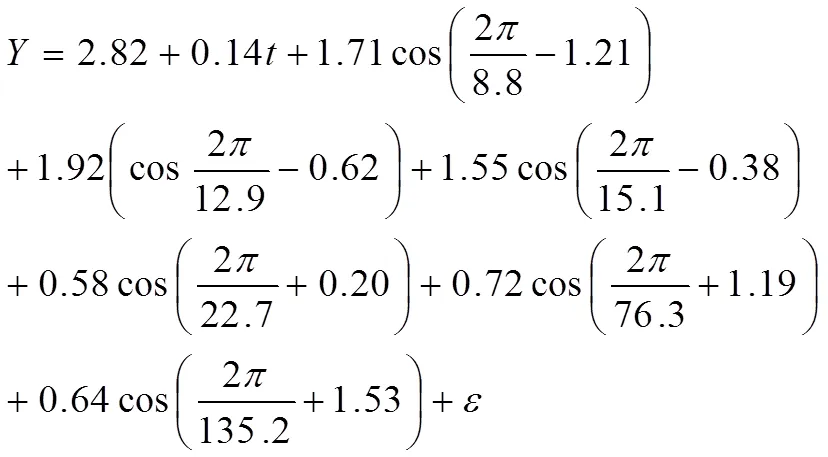
2.4 降水量预测

根据所建立的模型，对黄河三角洲2019年月平均降水量进行预测，并与实际降水量进行对比，结果见表2、图2和图3。

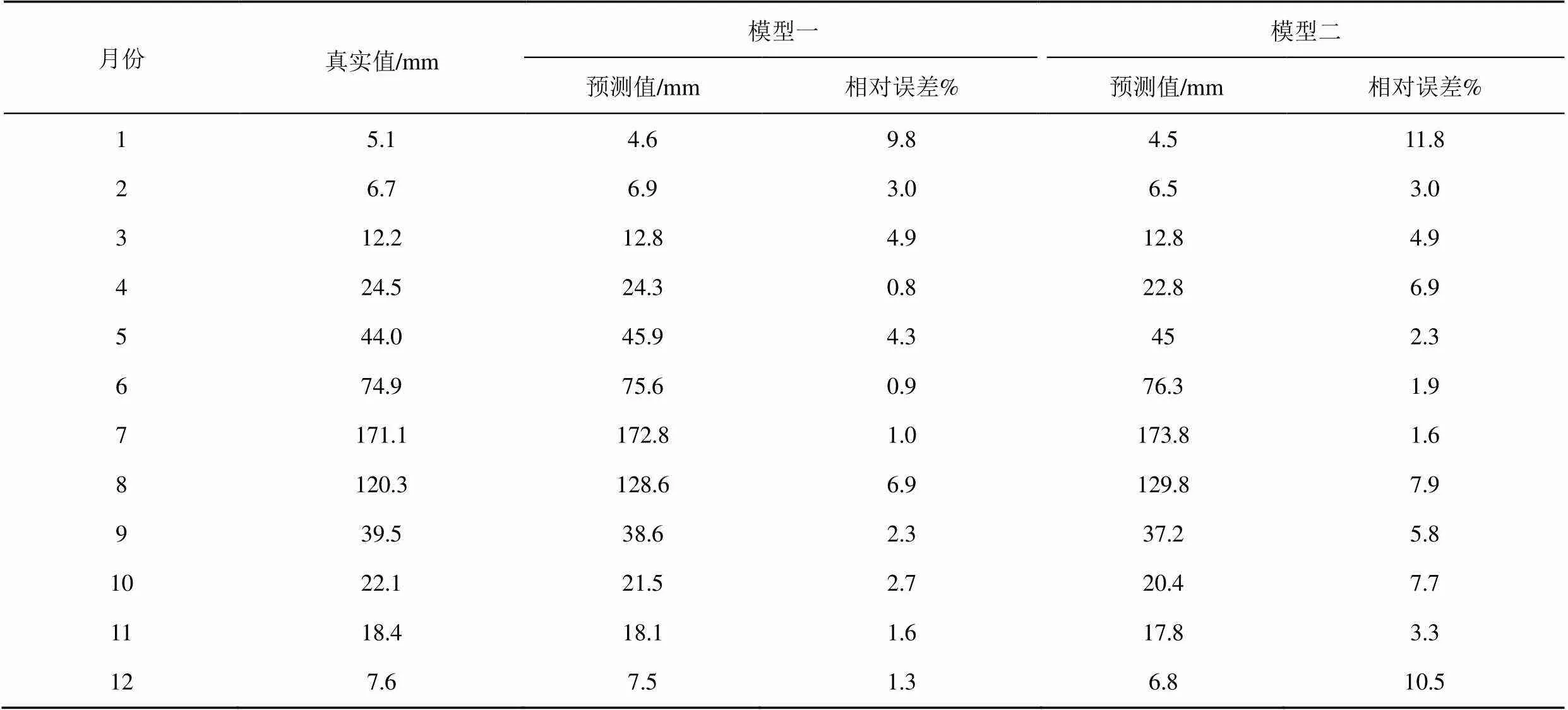
表2 2019年降水量预测值与实测值对比表

图2 模型一预测值与实测值对比图

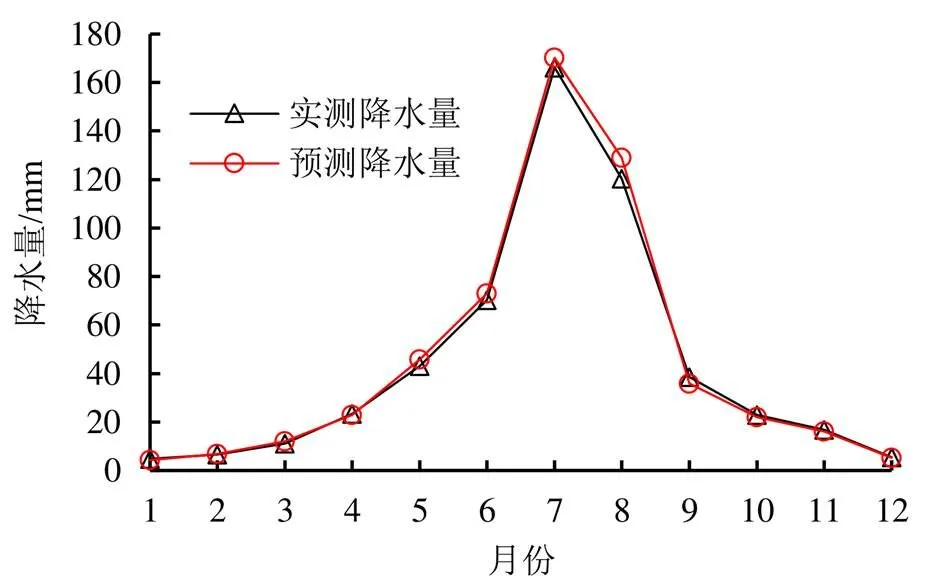
图3 模型二预测值与实测值对比图

由表2可以看出，模型一对黄河三角洲降水量的预测误差均在10%以下，相对误差平均值为3.3%，最大相对误差为9.8%，模型二对黄河三角洲降水量的预测误差均在12%以下，相对误差平均值为5.6%，最大相对误差为11.8%。2种模型预测精度均表现出较高水平，无论是否考虑初相位的影响，2个模型在1月预测误差均为年内最大，这可能与该时期为干旱期降水量量级较小有一定关系。

本次选用非特征年型2019年分别对模型一、模型二的预测数据进行误差检验分析，并取得了不错的效果，这在一定程度上说明2种模型在黄河下游降水量预测上具有一定的适用性。

3 讨论

降水的形成易受地形、气候、下垫面及人类活动等众多因素的相互影响，降水量时间序列一般都具有非线性、非平稳性的特点。降水量预测为降水量的定量研究、水资源的利用及河口治理提供科学依据，因此降水量非线性时间序列的预测十分重要。许多专家和学者采用各种方法对非线性时间序列进行建模预测，但是这些方法大部分是单尺度的[15]。近些年已有一些学者将EMD分解用于时间序列预测分析，取得了不错的成果[16]，但多为各分量累加预测，未能完全考虑高频IMF分量的预测误差。本研究对时间序列EMD分解后的不同尺度下的各分项进行Hilbert变换，得到其瞬时频率、周期以及初相建立非线性多尺度区域降水量预测模型，考虑了降水量数据在不同尺度上的演变特性对预测结果的影响，同时也降低了高频分量的预测难度，模型有较高精度。

模型一、模型二的具体参数是根据对黄河三角洲1954－2018年连续65 a月降水数据分解分析得到，因此2种模型对黄河三角洲降水预测具有较强的针对性，有助于提高预测的可信度。模型一相对误差平均值为3.3%，模型二相对误差平均值为5.6%，均小于国际水文组织认可的20%误差范围。与传统的降水量预测方法相比，时间序列模型精度为7.5%[15]，加权马尔科夫链法精度为6.9%[7]，ARIMA模型精度13.1%[8]，人工神经网络模型精度多在10%～20%之间[12]，本模型预测精度均较高，这表明黄河三角洲降水量时间序列具有显著的非线性特征，对其进行EMD分解，并进行Hilbert变换，新生成的序列在一定程度上能反映降水量内在的变化特征与演变机制，从而使得预测精度较高。

从研究结果看，在建模时不考虑初相位的模型一平均预测误差为2.70%，整体预测精度要优于考虑初相位的模型二，平均误差5.63%，说明对于初相的引入虽在一定程度上完善了模型，但由于初相位确定的过程中存在的误差可能影响整个模型的预测精度。在对12个月降水量预测精度的横向对比中发现，模型对4－7月的预测精度要优于其他8个月，与降水量年内分布具有负相关性。

本文仅仅针对已有实际降水量数据进行分析，从数据序列本身特征来揭示其演变规律，未来从下垫面变化等影响降水量的物理机制方面进行预测是需要进一步研究的重点。

4 结论

1）研究运用非线性多尺度模型对黄河三角洲1954—2018年连续65 a 780个月的降水量时间序列进行了EMD分解，得到6个IMF分量和1个残差分量，在一定程度上反映了研究区降水量变化的影响机制和驱动因素。

2）本文所建模型一预测误差在10%以下，相对误差平均值为3.3%，最大相对误差为9.8%；模型二预测误差均在12%以下，相对误差平均值为5.6%，最大相对误差为11.8%。

3）2种模型预测精度均较高，在建模时不考虑初相位的模型一平均预测误差为2.70%，整体预测精度要优于考虑初相位的模型二，平均误差5.63%，2个模型在1月预测误差均为年内最大，这可能与该时期为干旱期，降水量绝对值相对较小有一定关系。

本研究方法为降水量的快速较高精度的预测提供了一次理论实践探讨，有利于促进黄河流域生态系统长久健康发展。

[1] LIEBMANN B, MARENGO J A. Interannual variability of the rainy season and rainfall in the Brazilian Amazon basin[J]. Journal of Climate, 2001, 14(22): 4 308-4 318.

[2] ZENG W, YU Z, WU S H, QIN J B. Changes in annual, seasonal and monthly precipitation events and their link with elevation in Sichuan Province, China[J]. International Journal of Climatology, 2016, 36(5): 2 303-2 322.

[3] 王英, 曹明奎, 陶波, 等. 全球气候变化背景下中国降水量空间格局的变化特征[J]. 地理研究, 2006, 25(6): 1 031- 1 040, 1 148.

WANG Ying, CAO Mingkui, TAO Bo, et al. Variation characteristics of spatial pattern of precipitation in China under the background of global climate change[J]. Geographic Research, 2006, 25 (6): 1 031-1 040, 1 148.

[4] 刘田, 阳坤, 秦军, 等. 青藏高原中、东部气象站降水资料时间序列的构建与应用[J]. 高原气象, 2018, 37(6): 1 449-1 457.

LIU Tian, YANG Kun, QIN Jun, et al. Construction and applications of time series of monthly precipitation at weather stations in the central and eastern Qinghai-Tibetan Plateau[J]. Plateau Meteorology, 2018, 37(6): 1 449-1 457.

[5] 刘向培, 王汉杰, 何明元. 应用统计降尺度方法预估江淮流域未来降水[J]. 水科学进展, 2012, 23(1): 29-37.

LIU Xiangpei, WANG Hanjie, HE Mingyuan. Estimation of precipitation under future climate scenarios in the Yangtze-Huaihe region using statistical downscaling[J]. Advances in Water Science, 2012, 23(1): 29-37.

[6] 刘健文, 周小刚. SSA方法在气候时间序列分析和预测中的应用[J].气象科技, 1996, 24(3): 18-22.

LIU Jianwen, ZHOU Xiaogang. Application of SSA method in climate time series analysis and prediction [J]. Meteorological Science and Technology, 1996, 24(3): 18-22.

[7] 梁显丽, 宝秋利, 代海燕. 加权马尔科夫链在鄂尔多斯市年降水量预测中的应用[J]. 数学的实践与认识, 2021, 51(4): 161-171.

LIANG Xianli, BAO Qiuli, DAI Haiyan. Application of weighted Markov chain in prediction of annual precipitation in Ordos region[J]. Mathematics in Practice and Theory, 2021, 51(4): 161-171.

[8] 付明明. ARIMA模型在新疆喀什地区中长期降水量预测中的应用研究[J]. 地下水, 2019, 41(3): 142-144.

FU Mingming. Application of ARIMA model in prediction of medium and long-term precipitation in Kashi area, Xinjiang[J]. Ground Water, 2019, 41(3): 142-144.

[9] 杨沛羽, 张强, 史培军, 等. 黄河流域极端降水时空分布特征及其影响因素[J]. 武汉大学学报(理学版), 2017, 63(4): 368-376.

YANG Peiyu, ZHANG Qiang, SHI Peijun, et al. Spatiotemporal distribution of precipitation extremes and related implications across the Yellow River Basin, China[J]. Journal of Wuhan University (Natural Science Edition), 2017, 63(4): 368-376.

[10] 杜懿, 龙铠豪, 王大洋, 等. 基于机器学习方法的安徽省年降水量预测[J]. 水电能源科学, 2020, 38(7): 5-7, 41.

DU Yi, LONG Kaihao, WANG Dayang, et al. Annual precipitation prediction in Anhui Province based on machine learning[J]. Water Resources and Power, 2020, 38(7): 5-7, 41.

[11] 孔德萌, 李维德, 吴金冉. 基于协整理论的极限学习机模型在降水预测中的应用[J]. 水电能源科学, 2017, 35(9): 1-3, 12.

KONG Demeng, LI Weide, WU Jinran. Application of extreme learning machine model in precipitation prediction based on cointegration theory[J]. Water Resources and Power, 2017, 35(9): 1-3, 12.

[12] 何慧, 陆虹, 覃卫坚, 等. 人工神经网络在月降水量预测业务中的研究和应用综述[J]. 气象研究与应用, 2021, 42(1): 1-6.

HE Hui, LU Hong, QIN Weijian, et al. Research and application of artificial neural network in monthly precipitation forecast[J]. Journal of Meteorological Research and Application, 2021, 42(1): 1-6.

[13] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1 971): 903-995.

[14] 任博, 薛泽宇, 任全志, 等. 基于EMD的凌河流域降水径流预测模型研究[J]. 人民黄河, 2016, 38(6): 63-65.

REN Bo, XUE Zeyu, REN Quanzhi, et al. Rainfall runoff forecast application of BP prediction models based on EMD in linghe river basin[J]. Yellow River, 2016, 38(6): 63-65.

[15] 于保慧. 时间序列模型在辽西降水量动态预测的应用[J]. 东北水利水电, 2019, (3): 42-44, 54.

YU Baohui. Application of time sequence model in precipitation dynamic forecast in western Liaoning province[J]. Water Resources & Hydropower of Northeastr, 2019, (3): 42-44, 54.

[16] 马军, 陆甲, 赵金彪. EMD方法在广西夏季降水量预测中的应用[J]. 气象研究与应用, 2014, 35(3): 31-35.

MA Jun, LU Jia, ZHAO Jinbiao. Application of EMD Method in Prediction of Summer Precipitation in Guangxi[J]. Journal of Meteorological Research and Application, 2014, 35(3): 31-35.

Precipitation Forecast in Yellow River Delta Based on Nonlinear Multi-scale Mode

MU Yuzhu1，WANG Yanpeng1，ZHANG Fenghua1，QIAO Dongmei2*

(1. Henan Xinxiang Hydrology and Water Resources Survey Bureau, Xinxiang 453000, China;2. Farmland Irrigation Research Institute, Chinese Academy of Agricultural Sciences, Xinxiang 453002, China)

【】Precipitation is closely related to human production, life and ecology. The change of precipitation is related to the sustainable utilization of regional water resources, the protection of ecological environment and the development of economy and society, The research on the variation characteristics and evolution trend of precipitation has become a hot topic in the field of climate and water resources. Scholars and researchers has paid much attention on the accurate prediction of precipitation.【】The purpose of this paper is to improve the prediction accuracy of precipitation, and reflect the actual characteristics of precipitation. 【】Based on the advantages of empirical mode decomposition in the analysis and processing of nonlinear time series and other fields, Empirical Mode Decomposition (EMD) was carried out for the monthly average precipitation data of the Yellow River Delta Meteorological Station from 1954 to 2018, and a series of eigenmode functions were obtained. Hilbert transform was performed on IMF, and on this basis, two multi-scale forecast models of precipitation in the Yellow River Delta were established.【】The results showed that there were periods of 9, 13, 23, 76 and 135 months in precipitation in the Yellow River Delta, and 9-month fluctuations were the main ones;The 65-year monthly average precipitation data was predicted. The relative error of the model 1 was between 0.9% and 9.8%, and the relative error of the model 2 was between 1.6% and 11.8%. When modeling, the average prediction error of model 1 without considering the initial phase was 2.70%, and the overall prediction accuracy was better than that of model 2 considering the initial phase.【】The fitting accuracy and significance of the two models meet the requirements.

precipitation; time series; multiscale; EMD; predict

S161.4

A

10.13522/j.cnki.ggps.2021149

1672 – 3317（2021）08 - 0123 - 06

穆玉珠, 王燕鹏, 张凤华, 等. 基于非线性多尺度模型的黄河三角洲降水量预测[J]. 灌溉排水学报, 2021, 40(8): 123-128.

MU Yuzhu, WANG Yanpeng, ZHANG Fenghua, et al. Precipitation Forecast in Yellow River delta Based on Nonlinear Multi-scale Mode[J]. Journal of Irrigation and Drainage, 2021, 40(8): 123-128.

2021-04-14

穆玉珠（1974-），女，河南新乡人。工程师，研究方向为水文水资源。E-mail: muyuzhu1020@126.com

乔冬梅（1978-），女。副研究员，硕士生导师，博士，研究方向为水资源与水环境。E-mail: qiaodongmei78@163.com

责任编辑：赵宇龙