高温环境下海洋平台防爆墙结构冲击动力响应特性研究

2021-09-02薛鸿祥袁昱超唐文勇

上海交通大学学报 2021年8期

王锐，薛鸿祥，袁昱超，唐文勇

(上海交通大学海洋工程国家重点实验室，上海 200240)

海洋平台等海洋装备是目前人类获取海洋资源的重要工业设施.火灾产生的高温会导致结构材料的性能发生变化，使得结构产生应力和应变.同时，火灾引发爆炸的可能性较大，而爆炸产生的冲击荷载对海洋平台结构的安全造成极大威胁.设置在危险区域的防爆墙作为目前海洋平台上的重要保护设施，其抗爆性能需要特别关注.

在理论方面，Soleiman-fallah等[1]以单自由度法(SDOF)为基础，提出将防爆墙结构简化为梁和弹簧的组合模型，但弹簧刚度值需要通过大量实验才能确定.Syed等[2]指出非线性有限元数值方法可以解决SDOF方法无法捕捉和预测连接结构响应以及波纹板局部应变的问题.Rahman等[3]使用计算流体动力学(CFD)方法模拟不同海洋平台的油气爆炸荷载工况，并在此基础上进行有限元分析(FEA).在实验方面，利物浦大学团队[4]制作了3个具有不同柔性连接长度的1/4比例的防爆墙结构，并将其放置于脉冲压力产生装置中进行模拟碳氢化合物爆炸荷载的冲击试验.

上述研究工作主要针对防爆墙在常温环境下的冲击响应问题，而徐文晶[5]指出海洋平台发生油气燃爆事故前往往伴随快速升温过程，高温会对材料的力学性能和结构强度造成影响.因此，以往研究仅考虑单因素的分析尚不够充分，还需要开展高温环境对海洋平台结构，特别是对防爆墙结构的动力响应特征研究.本文通过选取合适的建模和计算方法，并基于非线性有限元法，对高温环境中受爆炸冲击的防爆墙结构的动力响应进行数值模拟，分析典型防爆墙结构在不同荷载类别和温度下的失效模式，相关研究可为防爆墙结构设计提供参考.

1 基本理论

防爆墙受爆炸荷载的结构动力响应基本方程为

(1)

式中：M、C和K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵；T为温度；P(t)为与时间t相关的冲击荷载；x为节点位移矢量.

在进行冲击动力响应分析前，应先进行热力分析以确定高温影响产生的初始应力和应变.热应力对温度场的耦合影响不大，因此可以将结构热问题简化为单向耦合过程.根据热平衡条件，物体内无热源时，在分析域Ω内的热传导方程为

(2)

式中：ρ为物体密度；c为比热容；kx、ky和kz分别为x、y和z方向的导热系数.

初始温度(To)条件：

T(x,y,z,t)=To

(3)

边界物体换热条件：

(4)

式中:k1为表面导热系数；n为结构表面外法线方向；f(t)为表面热流密度.

对流辐射条件：

qxnx+qyny+qznz=α(Tg-Tb)

(5)

式中：qx、qy和qz为热通量；nx、ny和nz为法线方向；α为综合传热系数；Tg和Tb分别为环境和结构温度.高温影响产生的初始应变为

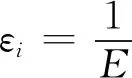
(6)

式中：E为弹性模量；ν为泊松比；σi、σj和σk为应力.根据内力平衡原则可以进一步求解高温产生的初始应变和应力.

2 数值分析模型与有效性验证

2.1 计算模型

数值分析模型基于利物浦大学实验中选取的海洋平台上部模块典型的防爆墙[4]，结构模型主要包括：波纹板、角钢1、角钢2和部分工字型梁.沿波纹板宽度方向选取4跨波纹宽度，其中波纹板单跨波纹宽880 mm，纵向长 3 660 mm，槽深162 mm，厚8 mm；角钢1(刚性角钢)和角钢2(柔性角钢)的厚度分别为16 mm和12 mm，具体模型信息如图1所示.根据Kim等[6]对防爆墙有限元模型的网格敏感性和网格质量的研究结论，本文使用Abaqus有限元软件进行仿真，波纹板采用三维连续的通用壳单元S4R，连接部分采用C3D8R三维实体单元建模，壳单元与实体单元连接处采用壳-实体耦合单元.波纹板网格尺度取16 mm，连接结构局部细化.波纹板上下的连接结构端部为全固定约束，而波纹板边缘边界条件经分析可视为对称约束.

波纹板、角钢1和角钢2均采用具备高延展性的316L材料，工字型梁为Q235钢.常温下材料的性能均根据所测材料的静、动力拉伸试验[4]确定，并结合动态应变率影响，对静力拉伸作用下材料的属性进行修正.选取Cowper-Symonds本构模型，具体参数如表1所示.其中，ρ为密度，σy为y方向的应力，σb为结构应力.

图1 模型几何尺寸(mm)Fig.1 Geometric dimensions of model (mm)

表1 模型材料参数Tab.1 Material parameters of model

2.2 实验对比验证

基于文献[4]，建立1/4比例模型，选取正、反方向各两组冲击工况的结构响应实验数据，与本文仿真结果进行对比.结构约束和冲击荷载方向如图2所示.荷载历程曲线根据实验数据输入，如图3所示.其中，p为压力，pmax为荷载峰值，正、负值分别表示正、反向冲击.

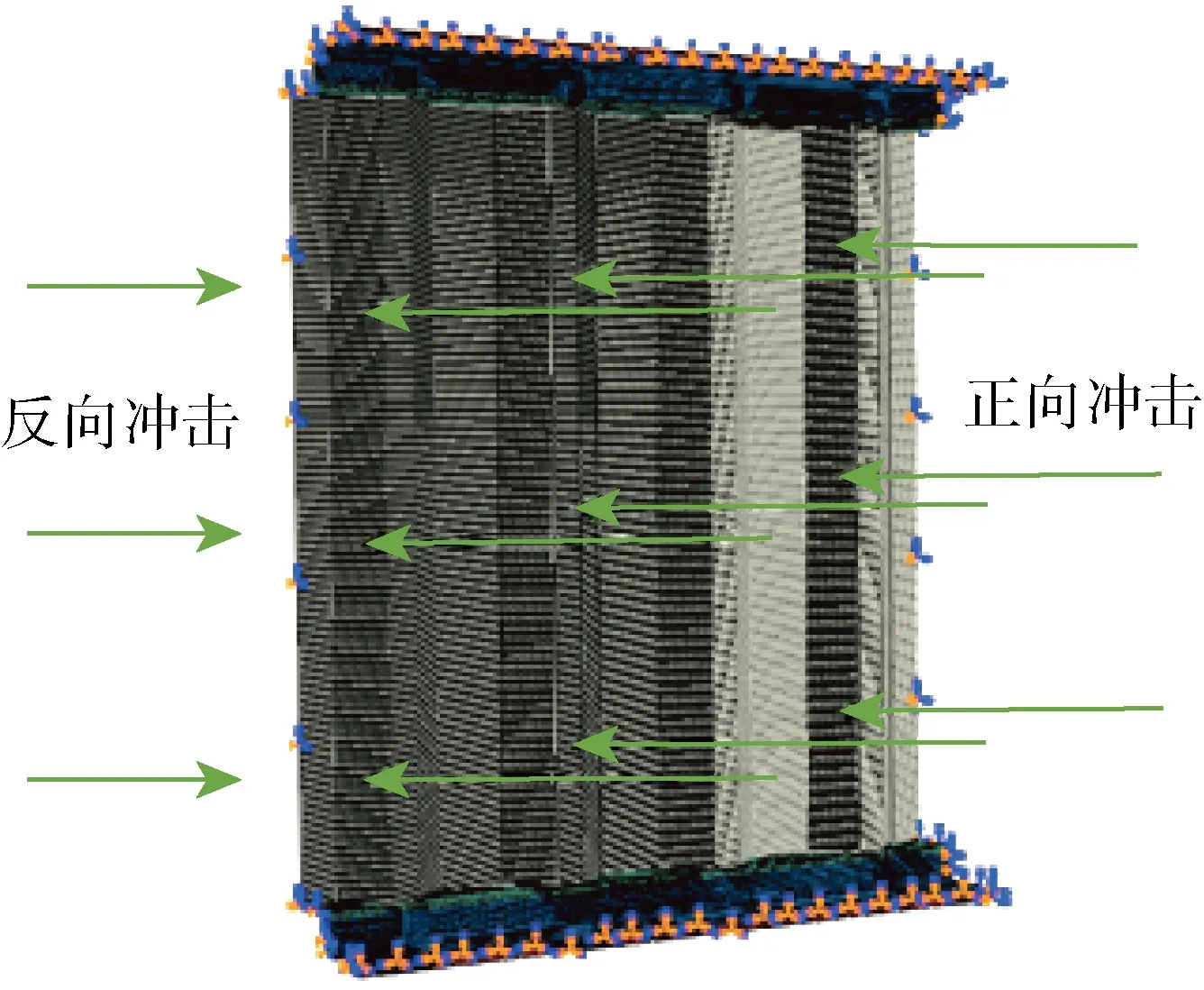
图2 约束和冲击荷载Fig.2 Constraint and impact load

防爆墙结构的自振周期较短，约为7～9 ms，相比于持续时间大于100 ms的碳氢合化物的爆炸荷载，结构响应可视为准静态.分别采用FEA准静态和FEA动态算法进行研究.准静态的本质可以理解为在缓慢加载的过程中，用连续静态分析模拟动力学问题的算法.模型在整个加载过程中是由一系列无限接近平衡的状态构成，模型在任意时刻所处状态均可视为静态平衡并进行求解，此时结构动能远小于内能.根据防爆墙受冲击后的应变特征，无永久应变为弹性范围，永久应变小于1/25跨长[7]为小应变范围，反之为大应变范围.图4为不同冲击荷载下的波纹板中心位置处的结构应变随时间的变化.其中，x0为实验位移，xmax为实验最大位移，xeve为实验永久位移.由图4(a)和4(b)可知，结构在弹性或小应变范围内不发生大应变及局部屈曲行为，在两种方法下，本算例均能快速求解，计算时长均小于1 h.但相比于动态算法，准静态算法输出的响应曲线无法很好地体现结构振动效果.

在图4(c)和4(d)中两种荷载均会导致结构发生大应变，本算例采用的准静态和动态算法均能模拟出结构局部大应变.在计算效率上，动态算法受最小时间步长限制，求解这类大应变与局部屈曲问题需要大量的时间增量，效率低.而准静态算法的计算效率则优于动态算法，且相较于结构应变的位移，结构自身的振幅极小，因此准静态算法输出的响应曲线尽管不能很好地体现结构自振但不影响其对结构响应的判断.综上所述，在弹性或小应变范围时，动态算法能更好地模拟响应曲线；在大应变范围时，准静态算法更高效且仿真结果可信.

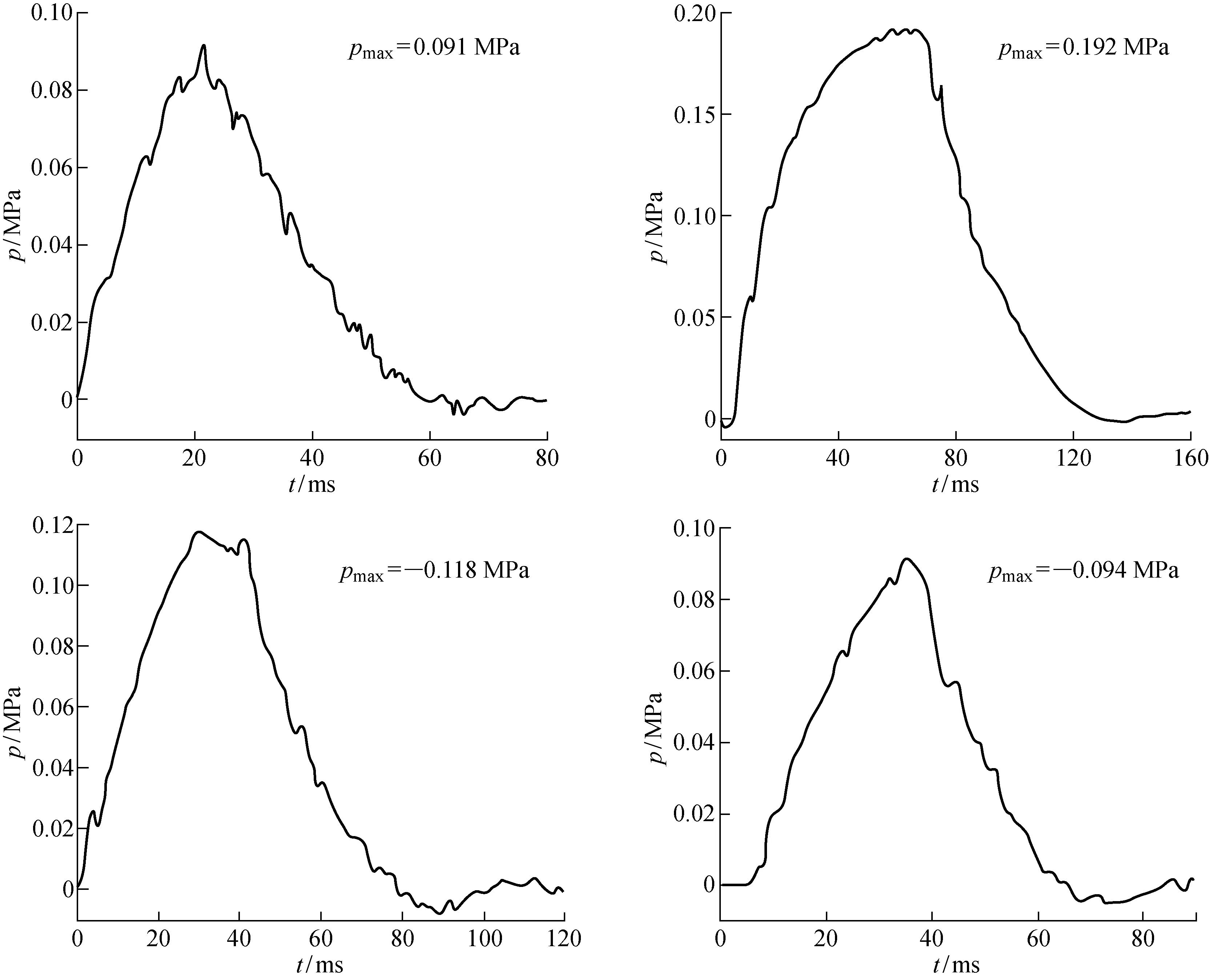
图3 荷载历程曲线Fig.3 Curves of load history

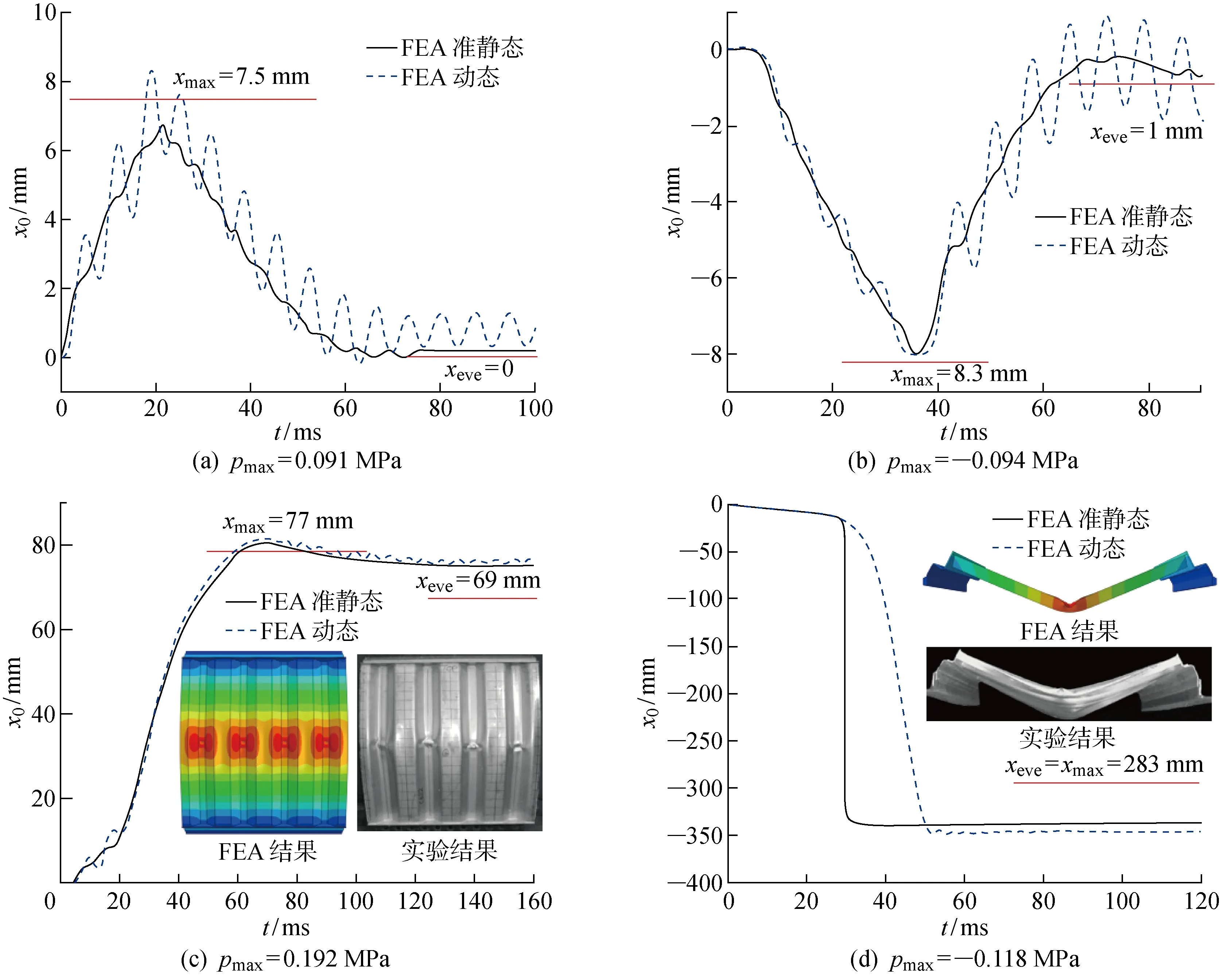
图4 波纹板中心位置处的结构应变时间历程曲线Fig.4 Curves of time history of structural deformation at the center of corrugated plate

由于受到实验条件限制，通常需要根据相似准则使用缩尺模型进行爆炸冲击实验.理论上缩尺模型与足尺模型结构强度一致，其静态流动应力相等，即σm=σf，但对于由应变率敏感材料制成的模型，应变率差异会影响分析结果.本模型材料使用Cowper-Symonds本构关系，有

(7)

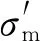
(8)

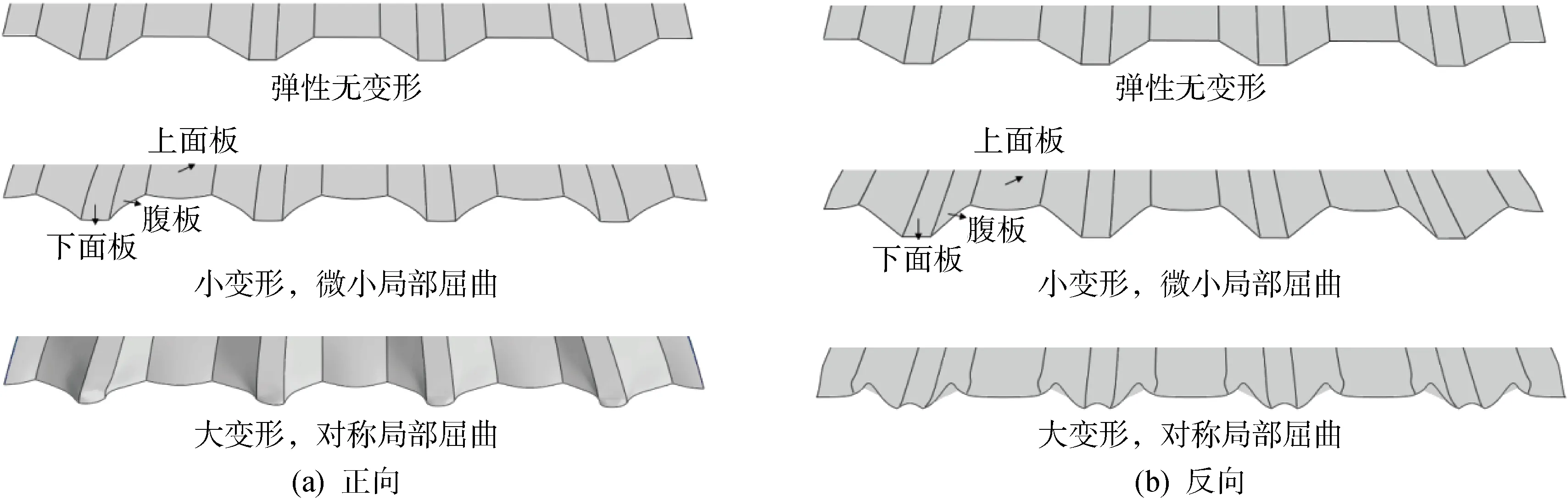
图5 常温冲击应变形式Fig.5 Impact deformation form at room temperature

2.3 不同冲击荷载水平下结构应变特征

海上平台上发生的爆炸通常为碳氢化合物爆炸，相较于炸药爆炸，其油气燃爆荷载升压时间可达100～300 ms，峰值压力较低，可以简化为三角形荷载.一般情况下，三角形荷载压力上升与下降的持续时间相近，爆炸荷载峰值为0.05～0.2 MPa.此外，为了研究结构的抗爆能力，还应该考虑超压.Mohamed等[8]对不同规范中的爆炸荷载进行了总结，并建议在抗爆设计中，主要构件的爆炸荷载超压(pe)应选取0.3～0.4 MPa.综合考虑防爆墙抗爆性能的方向性以及爆炸荷载大小和其加载速率对结构响应影响，设置总持续时间为400 ms，其中升压、降压时间均为200 ms，但荷载峰值不同，如表2所示.结果表明：在选取的常规和超压荷载冲击下，结构均不会产生撕裂，故暂不对防爆墙结构的撕裂情况展开讨论.

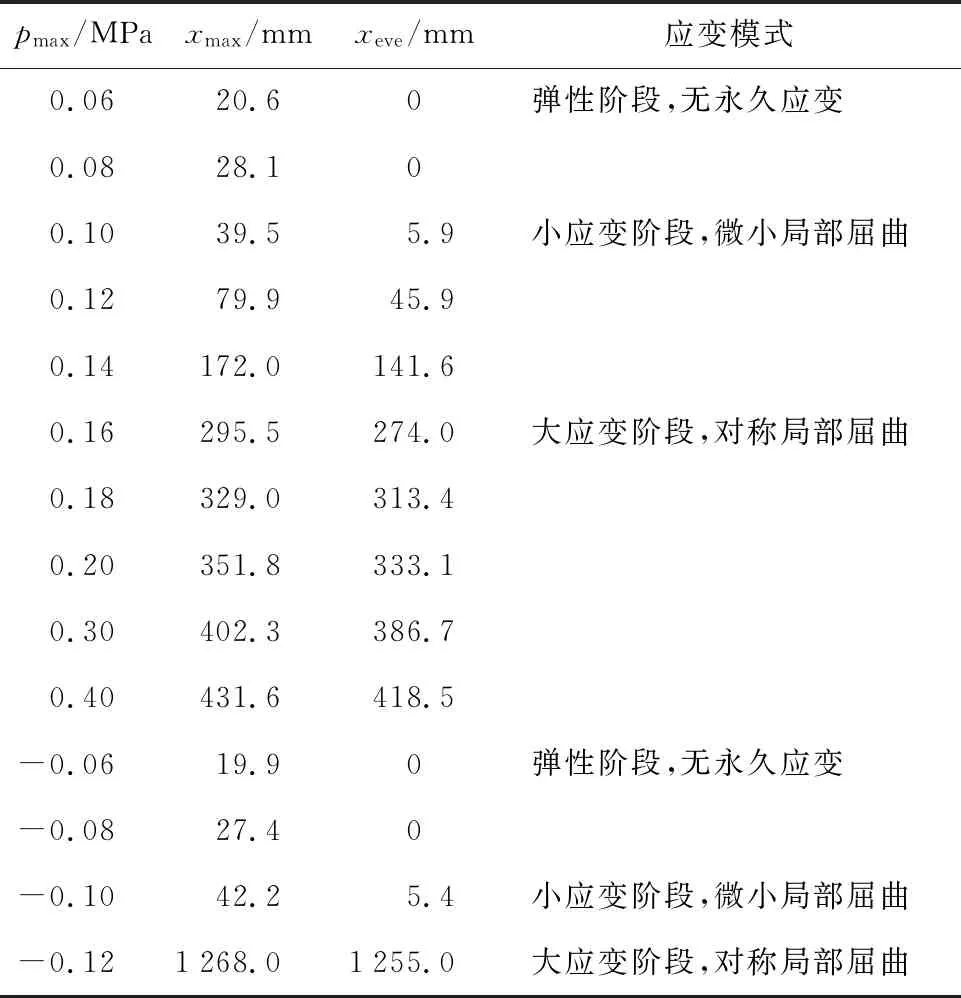
表2 不同荷载水平下结构响应Tab.2 Structural response at different load levels

通过上述分析，在正、反向冲击荷载作用下，波纹板的应变形式可以归纳为以下3类，如图5所示.

(1)弹性阶段：冲击结束后无永久应变，波纹板截面内无应变.

(2)小应变阶段：冲击结束后有轻微永久应变，波纹板截面内上面板最先屈曲，并带动腹板出现屈曲，下面板未出现明显屈曲.

(3)大应变阶段：冲击结束后有大永久应变，波纹板截面内上、下面板和腹板均受压出现明显屈曲，且屈曲对称.

结果表明：防爆墙板正向抗爆性能远大于反向抗爆性能，即结构抗爆性能具有明显的方向性，防爆墙板的抗爆性能主要对正向荷载而言.当pmax=-0.12 MPa时，波纹板中心观测点处的xeve=1 255.0 mm，远高于TN5规范中1/25～1/40倍跨长作为挠度极限[7]的建议值；当pmax=0.12 MPa时，xeve=45.9 mm，为小应变；当承受反向冲击时，结构的敏感度远高于受正向冲击的情况，在pmax=-0.08～-0.12 MPa区间内，结构会快速从弹性无应变到产生大应变.其中，在pmax=-0.10 MPa时，xeve=-5.4 mm，而在pmax=-0.12 MPa时，xeve=1 255.0 mm.说明在承受反向冲击时，结构会在超过抗爆能力临界点后快速崩溃.

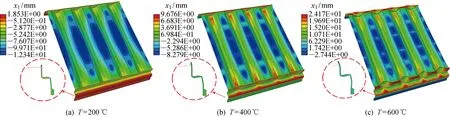
图8 不同结构温度下的连接结构横向位移Fig.8 Lateral displacement of connections at different structural temperatures

3 高温环境下防爆墙结构冲击动力响应特性

3.1 传热与热力分析

在高温场景中，升温会对材料性能产生较大影响：316L不锈钢与Q235钢的弹性模量、屈服强度、极限强度等都应考虑折减，同时导热系数、比热容和膨胀率随温度的变化都将影响分析结果.本文材料的热力参数参考文献[9]的试验数据选取.

首先采用顺序耦合法，选取外部升温条件，并结合材料与模型的传热属性，进行传热分析得到模型温度场，然后将温度场作为边界条件进行热力分析得到应力应变场，最后在应力应变结果的基础上进行冲击分析.根据前文分析，并结合实际高温叠加爆炸场景，高温侧与爆炸侧均设置在结构正向侧，选取波纹板中点A为结构温度观测点，由于波纹板厚度最小且接触散热面积小，所以点A温度为结构温度最高点.同时选取波纹板根部点B，角钢1腹板中点点C，角钢2腹板中点点D作为观测点.升温爆炸及观测点位置示意图如6所示，高温作用下各观测点位移如图7所示.

图6 高温爆炸场景和观测点分布Fig.6 Explosion scene and observation points

图7 高温作用下观测点位移Fig.7 Displacement of observation points at high temperature

升温时,连接结构因受热膨胀而产生正向位移，而点A处则凹向高温侧产生负向位移.随后，连接结构的正向位移逐渐变大，带动点A形成正向位移，但点A与点B产生的相对负向位移不断变大.随着结构温度上升至T=400 ℃时，波纹板出现明显折皱；当T=600 ℃时，波纹板连接处腹板边缘出现明显失稳，如图8所示.其中，x1为横向位移.

3.2 高温作用下的爆炸响应

为了探究实际场景下的高温作用对防爆墙结构响应的影响，选取点A为爆炸冲击发生点，爆炸冲击荷载持续时间为400 ms，仿真结果如图9所示.

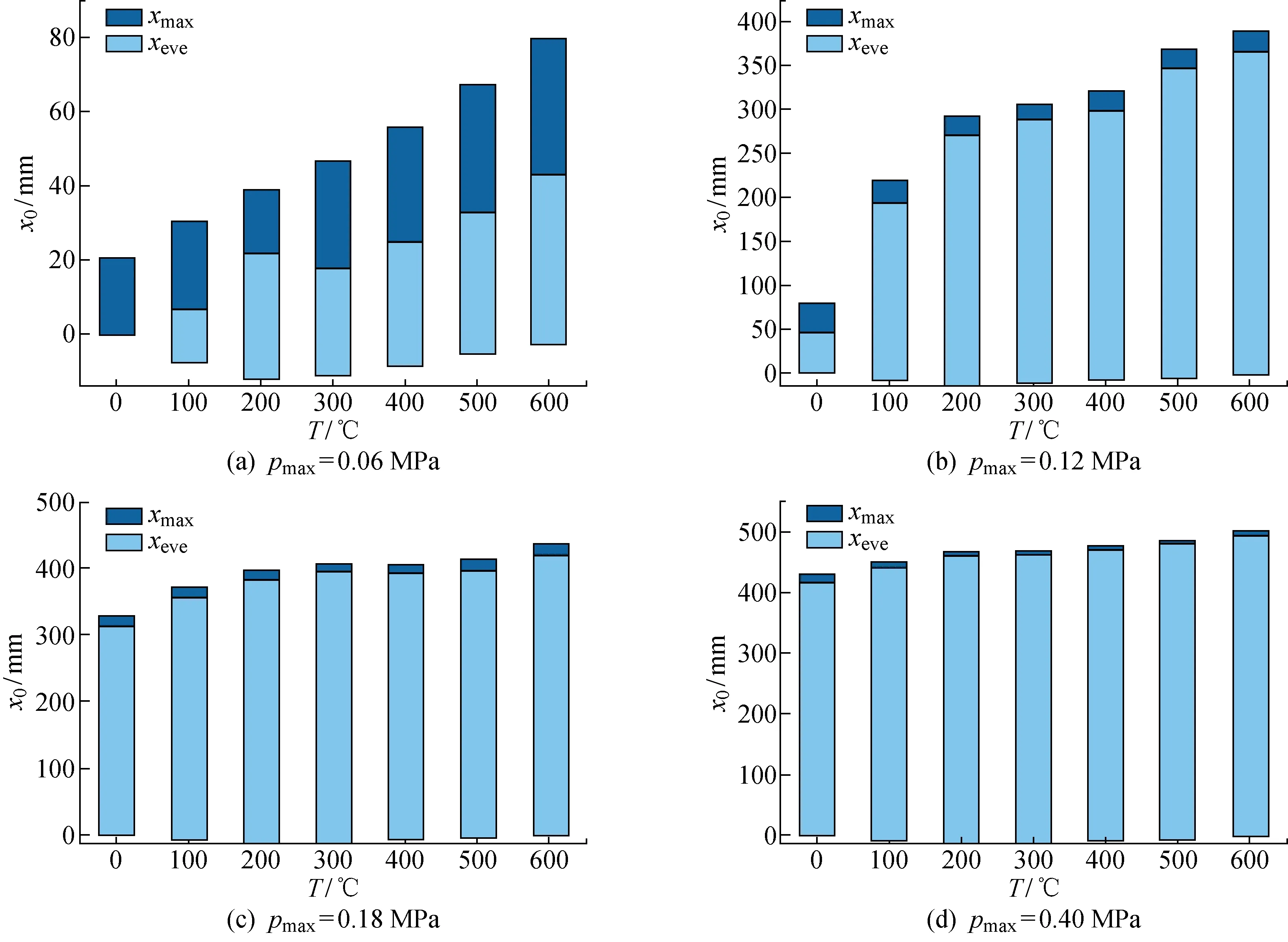
图9 不同温度下的冲击响应Fig.9 Impact response at different temperatures

当pmax=0.06 MPa时，防爆墙结构在常温时不产生应变，而在高温时会产生轻微的永久应变.在T=0～600 ℃的温度区间内，结构位移响应近似均匀地被放大，在T=600 ℃时结构位移幅值相较于常温时被放大了4.1倍.

当pmax=0.12 MPa时，防爆墙结构在常温时会产生轻微的永久应变，而升温至100 ℃时产生大应变；600 ℃时结构的位移幅值和永久应变相较于常温时分别放大了4.9倍和8倍.在T=0～200 ℃温度区间内，随着温度升高，结构位移响应显著增大；在T=200 ℃时局部应变依然对称，而在T=200～600 ℃时，局部应变不再对称.这是由于膜效应影响，结构位移和应变受升温影响的放大效应相对较小.

当pmax=0.18 MPa时，防爆墙结构在常温时即产生大应变.而在温度不断升高的过程中，位移幅值和永久应变都会进一步增大，但增大幅度远小于pmax=0.06，0.12 MPa的工况.常温时局部应变对称；而高温时，轻微横向位移扰动会被放大，导致局部产生扭转，不再对称.

当pe=0.4 MPa时，由于常温时结构已经产生较大永久应变，所以高温时位移响应的放大作用不明显，且由于大应变和结构软化，高温时的回弹不明显.

防爆墙模型面向危险区布置.升温后，承受正向冲击的波纹板横截面内的应变形式与常温情况下相比：无应变演化为小应变且存在微小局部屈服，而小应变演化为大应变且存在对称局部屈服，大应变演化为非对称局部屈服.其中，非对称局部屈服由于热应力分布不均，开始出现侧倾而横向移动，随后施加的冲击荷载加剧了其侧倾，如图10和11所示.