基于大涡模拟的圆柱绕流剪切层不稳定性
2021-09-02郭志远虞培祥欧阳华
郭志远,虞培祥,b,欧阳华,b
(上海交通大学 a.机械与动力工程学院;b.燃气轮机与民用航空发动机教育部工程研究中心,上海 200240)
开尔文-亥姆霍兹不稳定性(Kelvin-Helmholtz Instability)是指在一条速度不连续的切变线上产生涡度集中而导致的流动不稳定性,简称K-H不稳定性.在自然界中存在诸多K-H不稳定性,比如高空的波状云、风引起的水面波和云团锋面的不稳定现象等.在实际工程中,有学者发现后向台阶流[1]、翼型表面的分离流动[2]和轴流压气机旋转不稳定性[3]等现象都与K-H不稳定性存在一定的关联.对于经典的圆柱绕流问题,当雷诺数Re<49时,流动是定常的,在圆柱下游存在一对稳定的回流区;当49
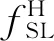
本征正交分解(POD)是最早提出的一种模态分解方法,POD能将高阶的、非线性的流场分解为若干个空间正交模态,按照模态的能量(即特征值)大小进行排序,进而选出流动的主要模态.动态模态分解(DMD)则是近年来新兴的一种数据处理方法,按照频率对系统进行排序,提取系统的特征频率,从而得出不同频率的模态对流场的贡献,进而分析复杂流场的非定常脉动的主要特征或者建立低阶的流场动力模型.POD将系统分解为低阶的空间正交模态,但这些模态会混叠多种频率成分,因此不利于流场的物理机理分析,而DMD方法可以得到模态的单一频率和扩散率(或耗散率),则有利于流场的结构分析和动力学分析[9-10].文献[11-16]使用DMD方法对50≤Re≤13 000圆柱绕流的数值与实验结果进行了模态分解,进而得到流场不同频率的模态特征,达到了分解流场和捕捉流场涡结构特征的研究目的.这些文献均准确地捕捉到卡门涡街的频率特征和模态,部分学者还对流场中的高频和低频特征开展了研究.因此,DMD方法是一种有效的数据处理方法,可以用来分析流场中的频率特征和模态特征.不过需要指出的是,这些学者并未关注剪切层K-H不稳定性.
本文将对Re=2 000,3 900,5 000的圆柱绕流开展大涡模拟,利用大涡模拟得到的速度场,通过传统的选择合适监测点的频谱分析和DMD分析的方法来探究圆柱绕流剪切层K-H不稳定性的特征,并对比分析两种数据处理方法的特点.
1 研究方法
1.1 数值方法与验证
本文考虑不可压缩流动,为实现高雷诺数的流动模拟,采用大涡模拟方法进行数值计算,因此,以滤波后的不可压缩Navier-Stokes方程作为控制方程.采用张量和爱因斯坦求和标记法,控制方程可表述为
(1)
(2)
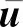
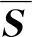
本文数值方法基于有限体积法,采用PISO(Pressure Implicit Split Operator)算法,时间和空间都采用二阶精度格式.
图1是圆柱绕流x-y平面的网格示意图.本文除角度以外,所有变量均采用无量纲单位(包括长度、速度等).其中,圆柱直径定义为D=1,流体域展向长度为πD,x方向长度为40D,y方向在圆柱两侧各有15D的距离,网格节点总数目是275万.算例的进出口边界条件分别是速度入口和自由出口,来流速度设为U0=1,流体域两侧和展向的边界条件均是对称边界条件,圆柱壁面是无滑移壁面.
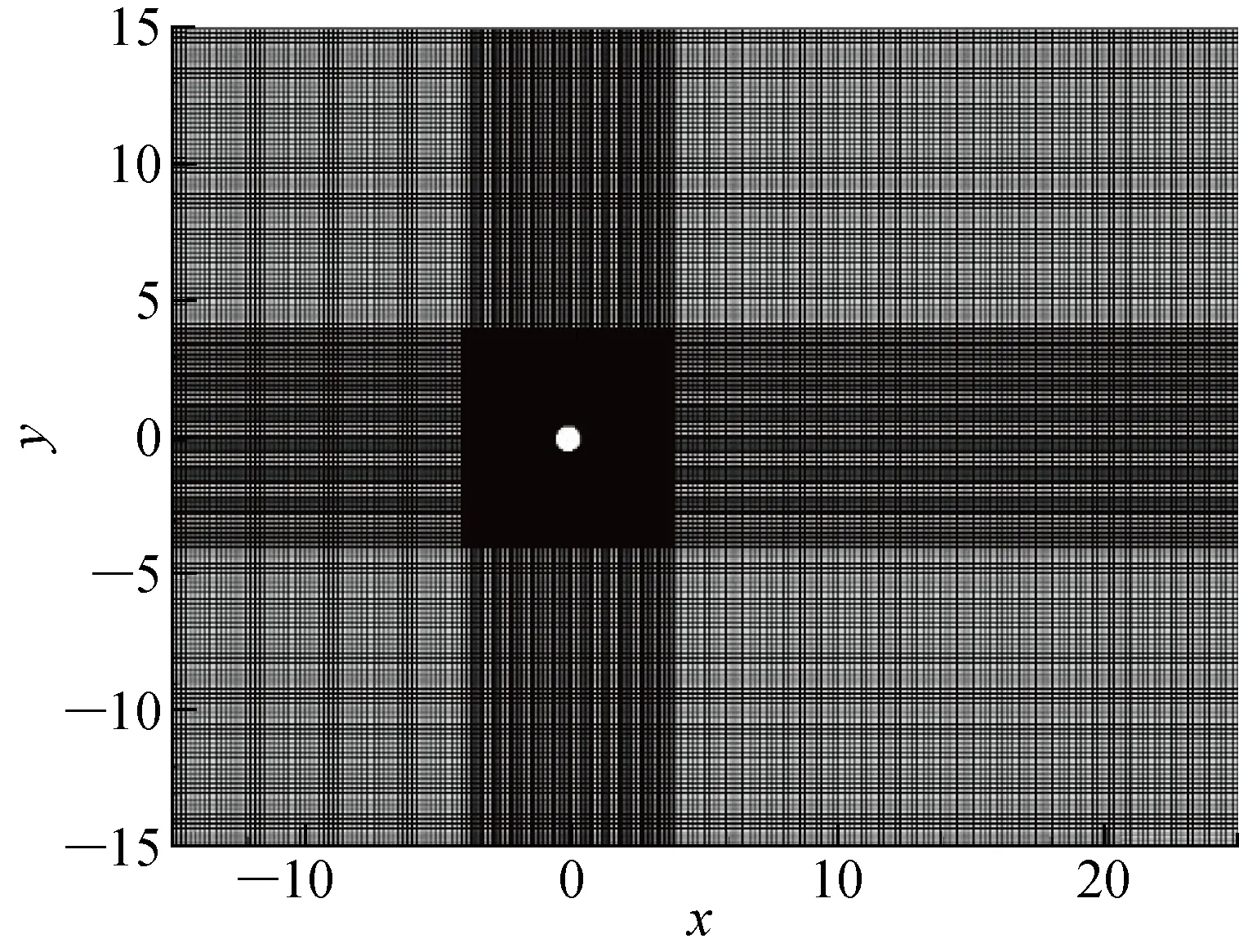
图1 圆柱绕流x-y平面的网格示意图Fig.1 Computational meshes for flow around a cylinder
本文先对Re=3 900的圆柱绕流问题开展数值模拟.对于该问题,目前不仅有大量LES的结果,而且也存在DNS的“标准解”,可用来检验不同LES方法的准确性.表1是斯特劳哈尔数(St=fD/U)、阻力系数(Cd)、升力系数均方根(Cl,rms)和圆柱表面背压系数(Cp,b)的比较结果.图2是圆柱下游轴线上(坐标为y=0,z=0.5πD)x方向的速度ux的时均分布.图3是圆柱壁面不同角度(θ)处的压力系数(Cp)分布图.图4和5分别是速度ux在不同位置处的时均值和脉动量均方根分布图.大涡模拟直接计算大尺度的涡旋而对小尺度涡旋使用亚格子应力的方式处理,因此在速度脉动值的统计上与DNS的结果略有差异,但根据表1和图2~5可以看出,本文大涡模拟的各个特征参数与已有研究结果非常接近,说明本文的LES结果是准确可信的.
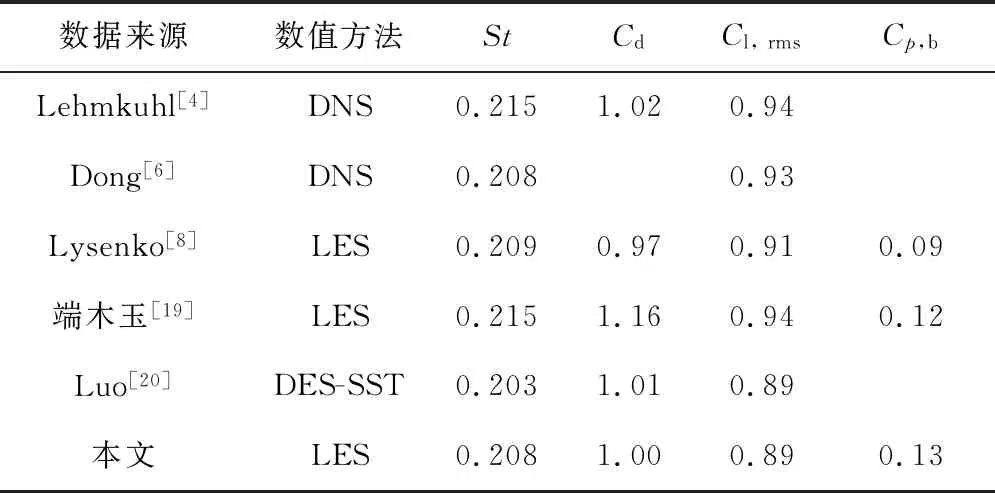
表1 Re=3 900的圆柱绕流特征结果对比Tab.1 Typical flow results at Re=3 900
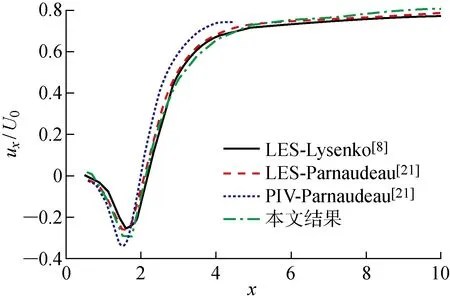
图2 Re=3 900圆柱绕流的流场轴线处ux沿流向分布的时均图Fig.2 Distribution of mean streamwise velocity ux along wake centerline at Re=3 900
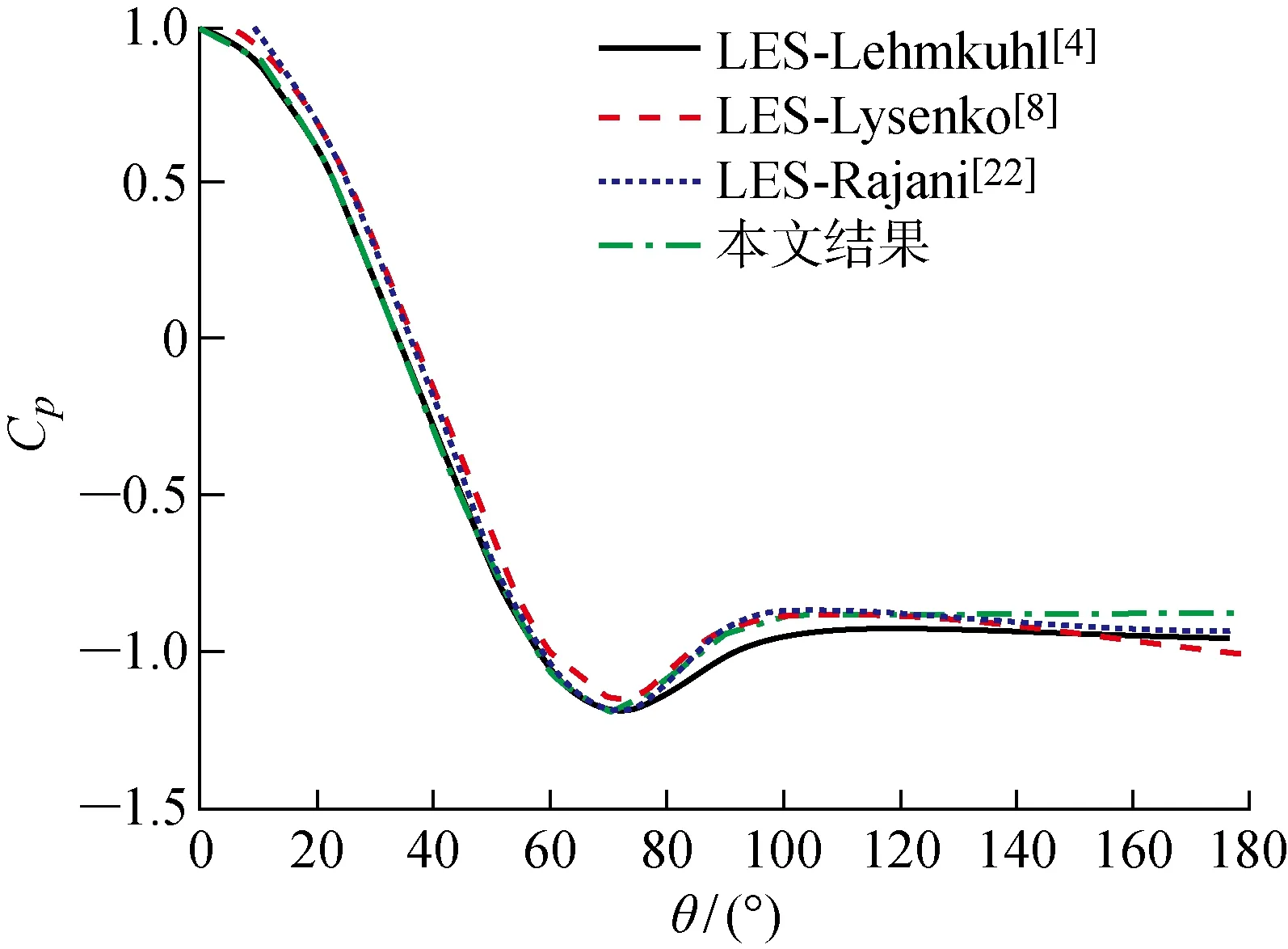
图3 Re=3 900圆柱绕流的Cp沿圆柱表面周向分布图Fig.3 Pressure coefficient on cylinder surface at different angles at Re=3 900
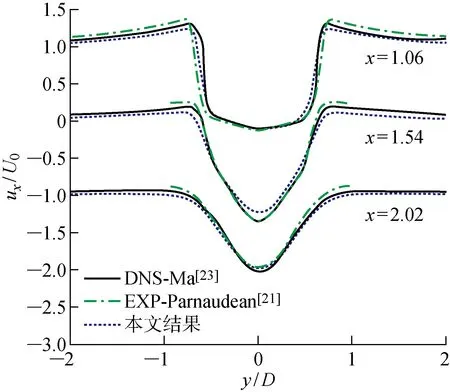
图4 Re=3 900的尾迹不同位置的时均流向速度剖面图Fig.4 Mean streamwise velocity at three locations in the wake of circular cylinder at Re=3 900
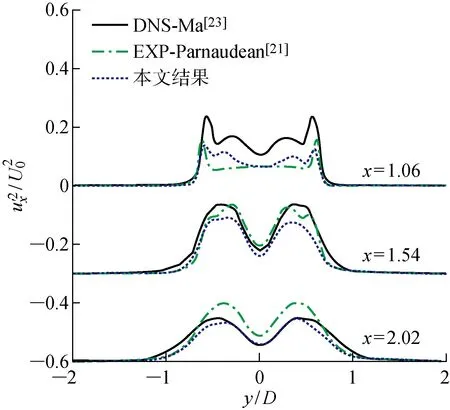
图5 Re=3 900的不同位置的流向速度脉动值均方根分布图Fig.5 Variance of streamwise velocity fluctuations at three locations in the wake of circular cylinder at Re=3 900
1.2 数据后处理DMD方法与验证
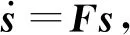
S=[s(t1)s(t2) …s(tm)]∈Rn×m
(3)
S#=[s(t2)s(t3)…s(tm+1)]∈Rn×m
(4)

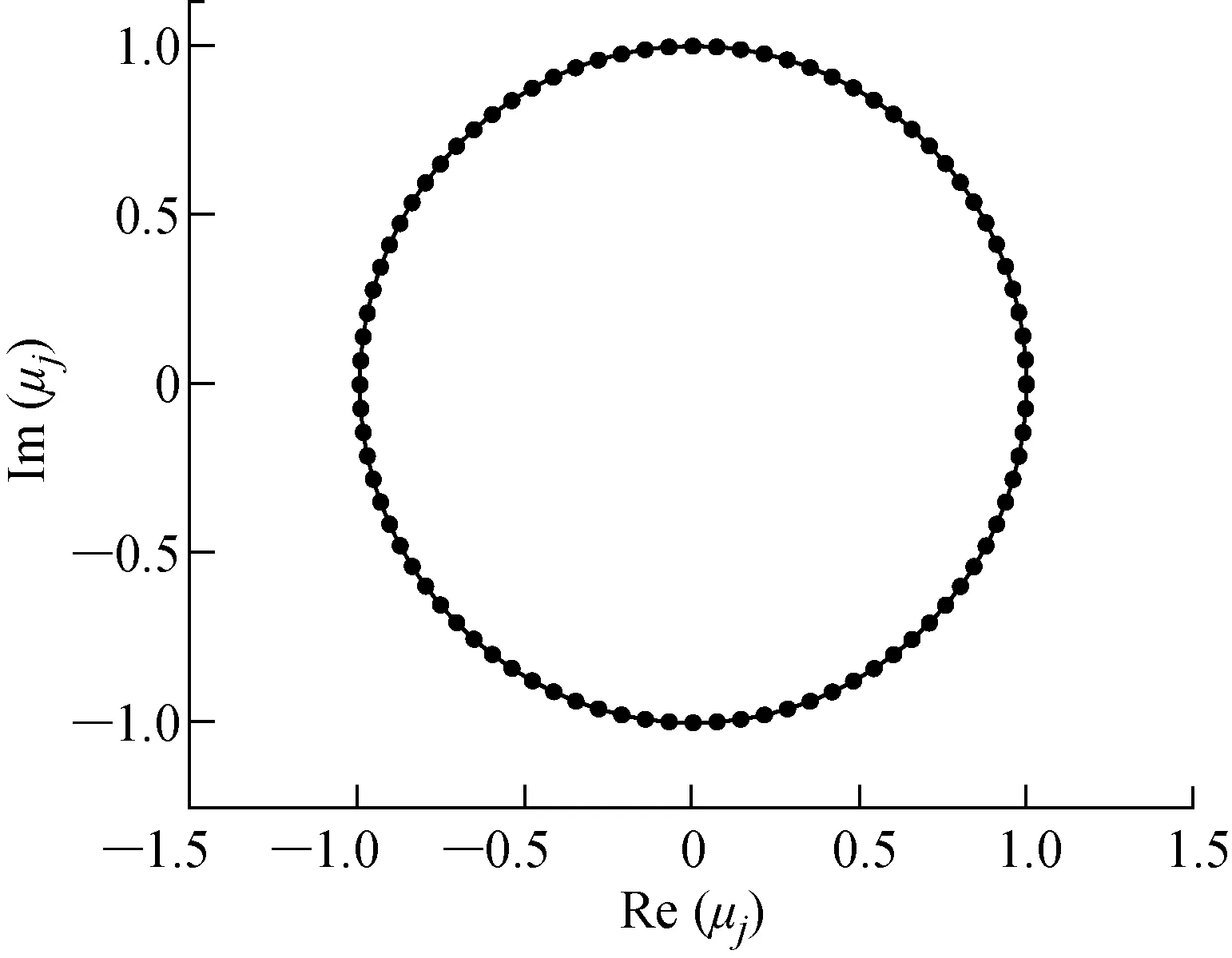
图6 Re=100圆柱绕流特征值分布图Fig.6 Distribution of eigenvalues of DMD at Re=100
本文选择Re=100的二维圆柱绕流的算例来验证DMD算法.Re=100圆柱绕流的St=0.165,选取2个卡门涡街周期的流场速度快照作为DMD的输入,每个卡门涡街周期内包含60个等时间间隔的取样.图6是DMD各阶模态特征值的实部和虚部所构成的点在单位圆附近的分布,其中横轴为特征值的实部,纵轴是特征值的虚部.在DMD特征值的分析中,当特征值对应的点位于单位圆内时,表示该模态是稳定模态;当特征值对应的点位于单位圆上时,表示该模态是周期性模态;当特征值对应的点在单位圆外,则表示该模态是不稳定(发散)模态.由图6看出,各阶模态特征值都位于单位圆上或者位于单位圆内同时又非常靠近单位圆,因此所有的模态都是周期性模态,此处的圆柱绕流处于稳定极限环状态.按能量‖Φ‖的大小排序,如图7所示.图中前5个频率(f)依次对应0,St0,2St0,3St0,4St0,其中St0=0.165.由此看出DMD方法可准确捕捉到圆柱绕流卡门涡街的主频及其各阶倍频.
根据特征值能量的大小提取DMD前5阶的模态与文献[24]的Re=100的DMD前5阶模态作对比,结果如图8所示.图8左侧由上到下依次是文献[24]前5阶模态(M1、M2、M3、M4、M5),图8右侧由上到下依次是本文得出的前5阶模态.由图8容易看出,两组DMD结果均捕捉到了圆柱下游尾迹处复杂的涡结构,每一阶模态的流场特征都是对称分布的,同时在圆柱下游的远处也都捕捉到了涡系的分布特征.两组DMD的结果基本一致,也证明了本文DMD算法的可靠性.

图7 Re=100圆柱绕流DMD能量谱Fig.7 DMD energy spectra at Re=100

图8 Re=100圆柱绕流的前5阶DMD模态对比图Fig.8 Comparison of first five dominant DMD modes for flow around a cylinder at Re=100
2 结果与分析
2.1 K-H不稳定性的特征频率
2.1.1传统的频谱分析结果 剪切层的速度梯度较大,是一个位置狭小的窄带,fSL对监控点的分布位置比较敏感,因此本文布置大量的监测点来捕捉fSL.通过比较不同位置处的速度的能量谱密度α,当监控点分布在如图9所示圆柱下游红色区域内的剪切层中时会得到比较好的结果.图10和图11分别是Re=3 900流场中的监控点A(0.62,0.7,0.5π)和B(0.8,0.9,0.5π)的y方向速度uy值的频谱图,图12和图13分别是Re为2 000和5 000的频谱图.根据图10和图11可以清楚地观察到,剪切层内的点A(0.62,0.7,0.5π)清晰地捕捉到了fSL的宽频信号,而位于剪切层外的点B(0.8,0.9,0.5π)虽然离剪切层距离较近,但仅仅捕捉到fVS的频率.根据对剪切层内的流场频谱分析,本文得出Re=2 000,3 900,5 000的fSL分别为1.051,1.463,1.584,相对应的fSL/fVS分别为4.98,7.05,7.75.
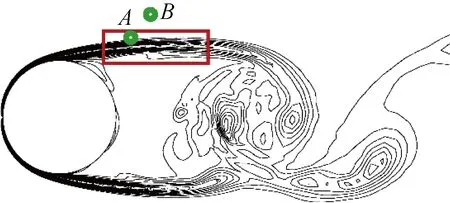
图9 Re=3 900的圆柱绕流剪切层示意图Fig.9 Schematic diagram of shear layer downstream a cylinder at Re=3 900
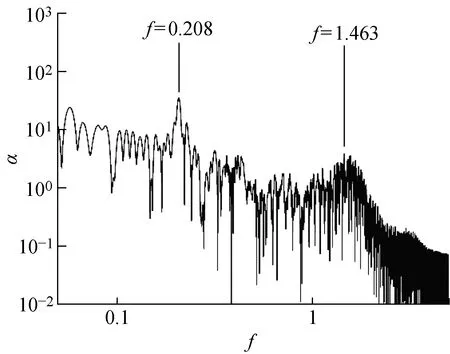
图10 Re=3 900流场中点A(0.62,0.7,0.5π)的频谱图Fig.10 Point A(0.62,0.7,0.5π)velocity power spectra at Re=3 900
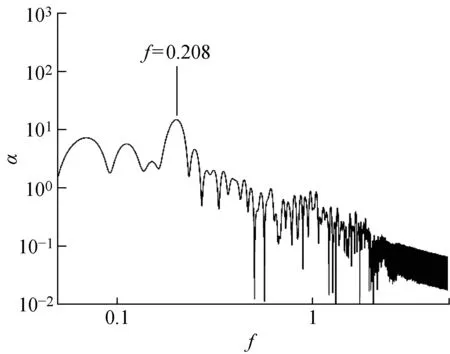
图11 Re=3 900流场中点B(0.8,0.9,0.5π)的频谱图Fig.11 Velocity power spectra of Point B(0.8,0.9,0.5π)at Re=3 900
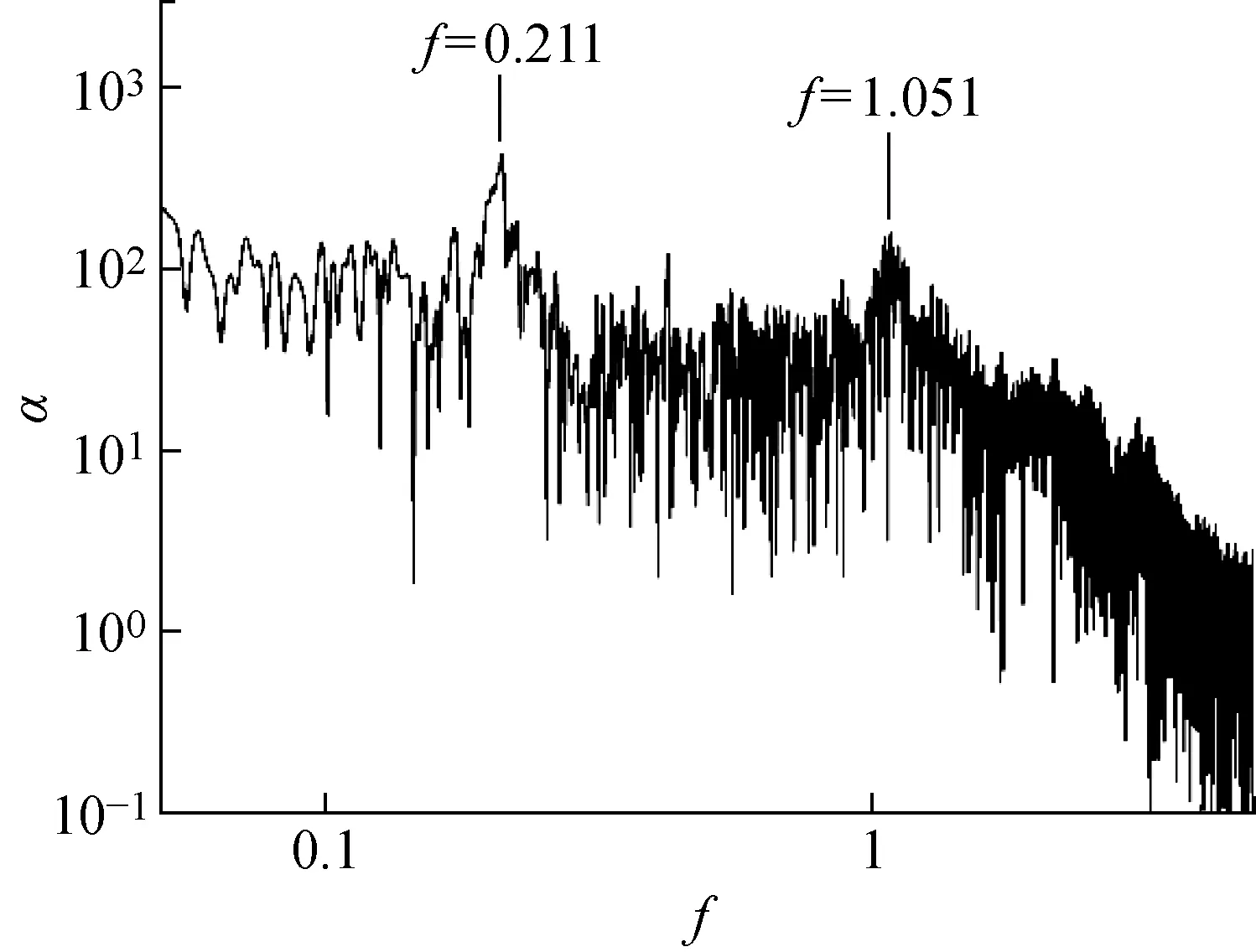
图12 Re=2 000流场中点A(0.62,0.7,0.5π)的频谱图Fig.12 Velocity power spectra of Point A(0.62,0.7,0.5π)at Re=2 000
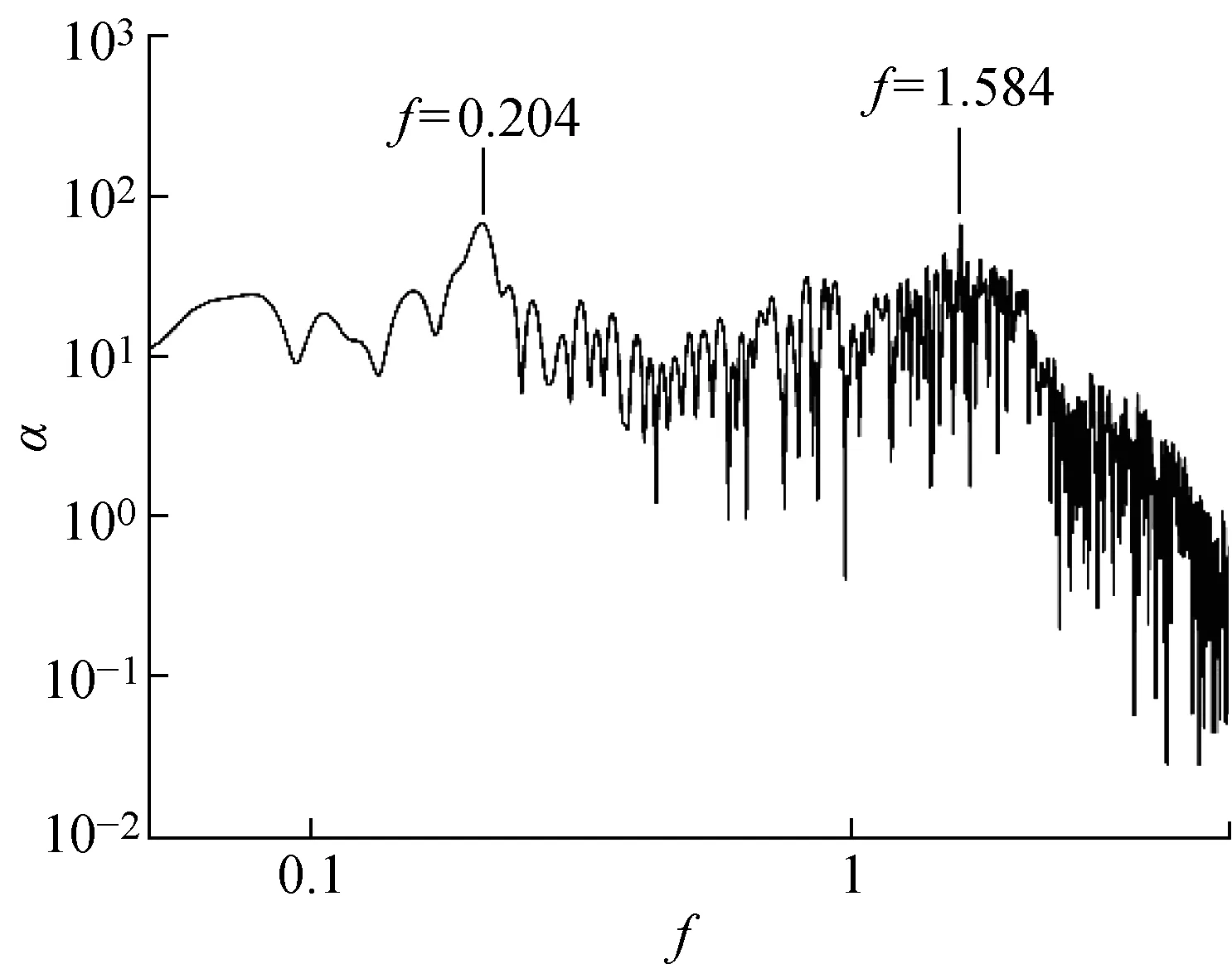
图13 Re=5 000流场中点A(0.62,0.7,0.5π)的频谱图Fig.13 Velocity power spectra of Point A(0.62,0.7,0.5π)at Re=5 000
2.1.2DMD的结果分析 将大涡模拟计算得到的等时间间隔的速度模值|U|和y方向的速度uy的“快照”进行DMD分析.以Re=3 900为例,从各阶模态特征值的实部和虚部的分布图14可以看出,绝大部分的特征值位于单位圆上,因此这些模态都是周期性模态,不会随着流动的发展而增长或者消耗.从图15看出,频率f=0是流场的主模态,其对应的能量值也最大,说明其主导了流场的基本形态.Re=2 000,3 900,5 000圆柱绕流的St≈0.21,从图15~17中可以清晰地看到在f=0.21附近有一个孤立的频率,这个频率的值与卡门涡街fVS相对应.由图15~17,在f=1.003,1.458,1.578附近也可以看到由模态特征频率组成的一个“宽峰”,这与频谱图中观测到的宽频信号fSL范围一致.Re=2 000,3 900,5 000相对应的fSL/fVS分别为4.63,7.03,7.52.
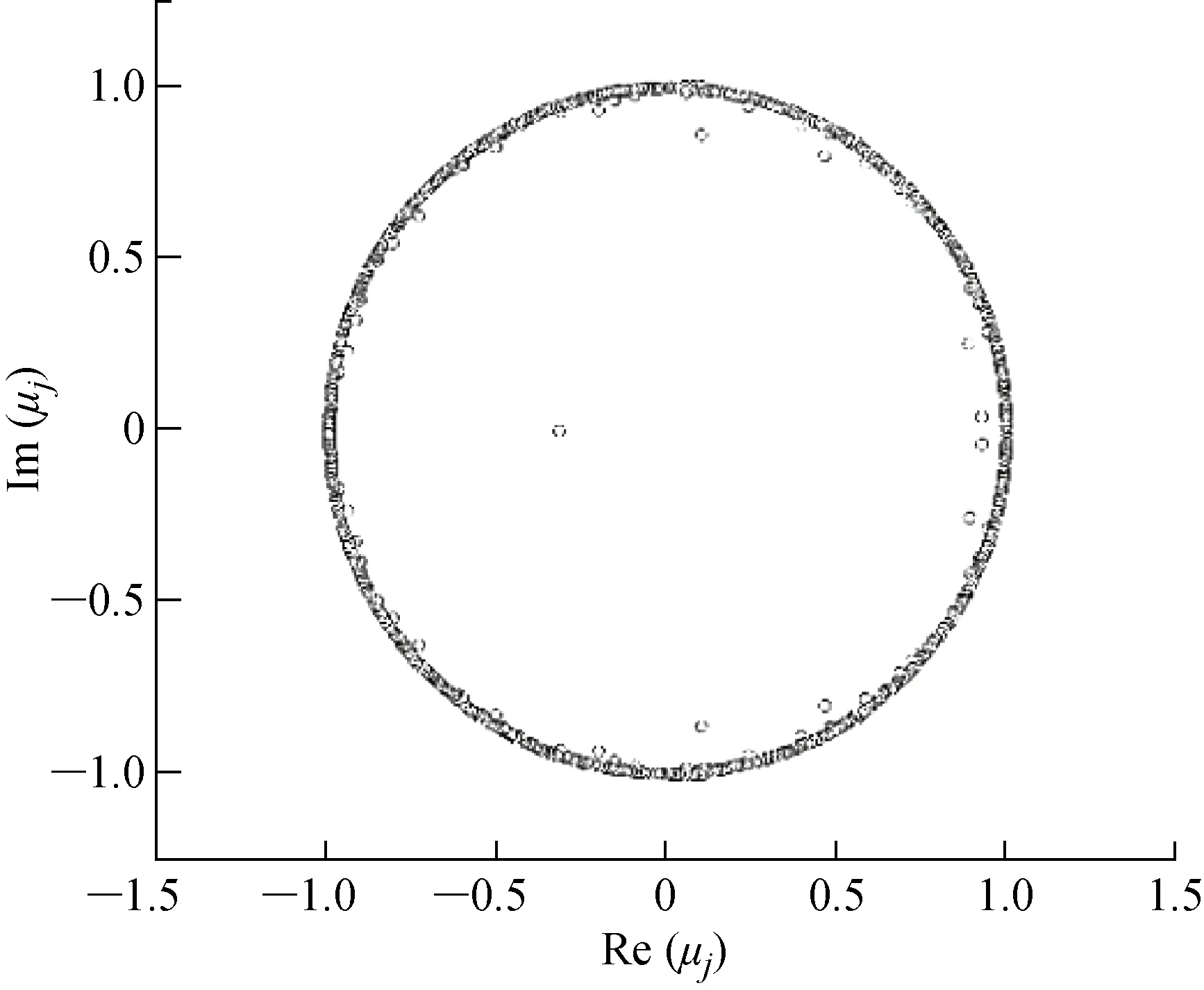
图14 Re=3 900的DMD特征值分布图Fig.14 Distribution of eigenvalues of DMD at Re=3 900
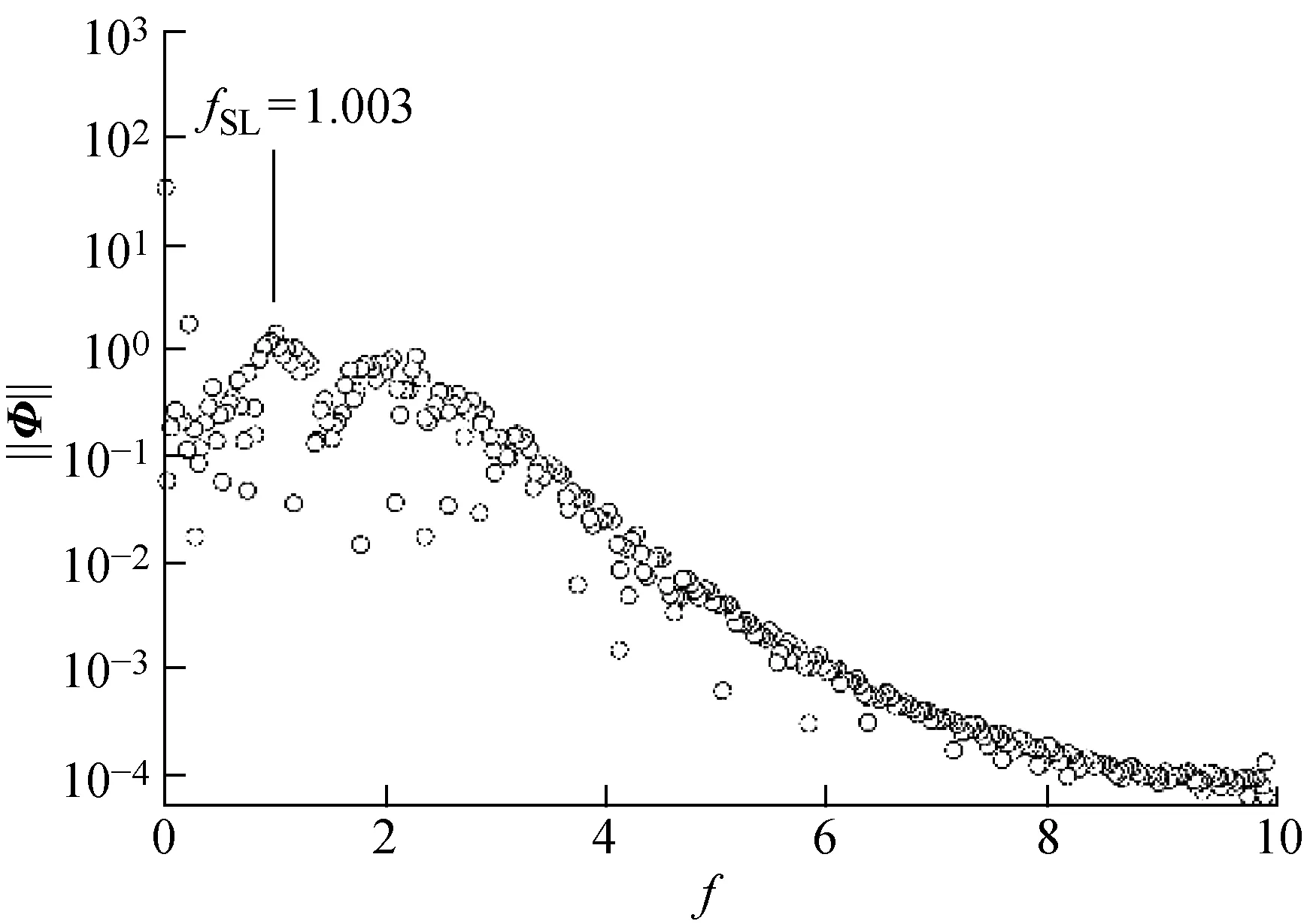
图15 Re=2 000 的DMD能量谱Fig.15 DMD energy spectra at Re=2 000
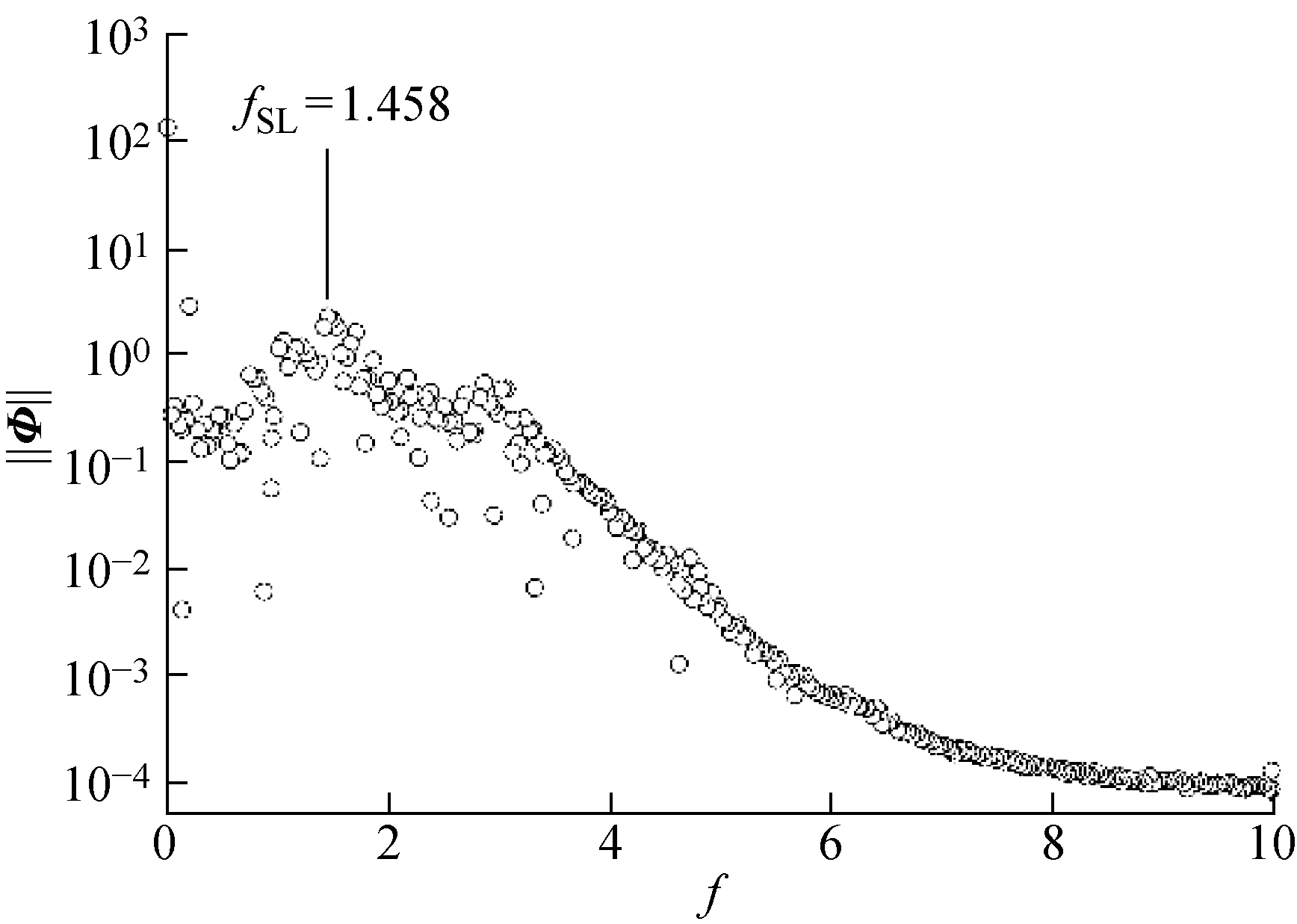
图16 Re=3 900 的DMD能量谱Fig.16 DMD energy spectra at Re=3 900
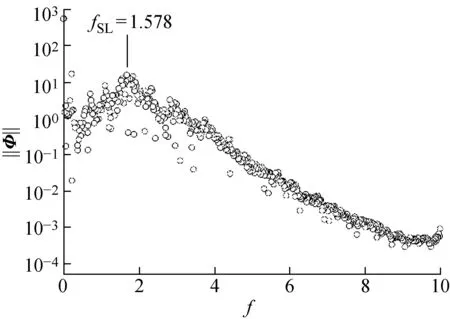
图17 Re=5 000 的DMD能量谱Fig.17 DMD energy spectra at Re=5 000
2.1.3两种后处理方法的比较 由图18看出,频谱分析和DMD的后处理方法都比较准确地捕捉到fSL,并与已有的DNS结果相一致.DMD方法与频谱分析的方法相比,无需在流场中精心布置监测点即可得到fSL的宽频信号,同时DMD特征频率是离散的点,峰值fSL的选取更加方便和准确,没有位置选取这样的人为因素干扰.DMD频率离散化的特点为fSL的判断提供了一个更好的手段.
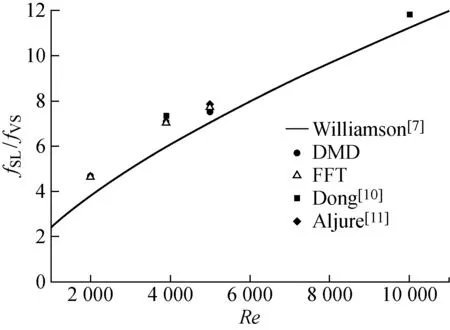
图18 fSL/fVS与Re的关系图Fig.18 Ratio of shear layer frequency/vortex shedding frequency versus Re
2.2 K-H不稳定性的特征流场
选取f=0,fVS,fSL分别对应的模态M0,MVS,MSL作图,如图19所示.从图19中看出,M0是基本对称分布的流场形态,表征了因圆柱的存在阻碍流体流动而造成的整个流场波动的特征.卡门涡街对应的模态MVS也呈现出对称的特性,并沿着来流方向往下游传播,与Re=100的卡门涡街频率fVS所对应的模态有许多相似之处.剪切层K-H不稳定性MSL的模态图在圆柱下游的剪切层区域内捕捉到许多细小的涡结构,这些涡团的位置关于圆柱也显示出一定的对称性.剪切层两侧的速度差诱发了K-H不稳定性,导致大量细微的涡旋产生于此,其在频率图上的表现则为宽频信号的凸起.
比较不同雷诺数下fSL对应的模态图MSL,可以发现随着雷诺数的增加,剪切层不稳定性伊始的位置向着来流方向移动,更加地靠近圆柱,并且较高雷诺数下的剪切层不稳定性消逝的位置比低雷诺数的位置也更加靠近圆柱.这个现象说明,雷诺数越大,剪切层K-H不稳定性发展得越快,消逝得越早,意味着剪切层的在x方向上的跨度越小.
在剪切层区域附近,uy的波动比模值 |U|更加显著,因此可以选择uy作为DMD的输入来进一步研究剪切层模态的特性.从图20看出不同雷诺数下的MSL模态图表现出很大的相似性:在圆柱下游的两侧均有序地排列着若干个涡旋并明显地表现出了一定的对称性,涡旋所在的位置也对应于以模值 |U|作DMD分解得到的MSL模态中的剪切层区域.不论是以模值 |U|还是uy作为DMD的输入,模态分解得到的剪切层不稳定性的区域是统一的.
剪切层区域内各个涡旋的直径大小差异并不大,与文献[6]中某个瞬时速度矢量场中剪切层涡旋产生的位置和大小相吻合.速度梯度的剪切作用在剪切层处产生了大小不同的涡旋,由此推测剪切层K-H不稳定性宽频信号里的不同频率对应着直径大小不同的涡旋.
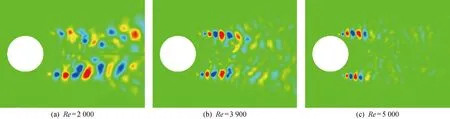
图20 不同Re下uy的剪切层模态图Fig.20 Shear layer modes of uy at different Re values
3 结论
本文使用大涡模拟的数值计算方法,对Re=2 000,3 900,5 000的圆柱绕流问题开展了研究,通过傅里叶变换频谱分析和DMD分析两种不同的数据处理方法,得到了比较一致的剪切层K-H不稳定性频率.本文同时用DMD方法研究了不同雷诺数对剪切层模态特征的影响.通过对比分析,发现在剪切层附近的位置生成了若干个平行于来流方向的涡旋并向下游传播,涡旋的位置关于y=0的轴线对称分布.随着雷诺数的增加,剪切层的不稳定性发生和消逝的位置都更加地靠近上游,并且剪切层的区域变得更小.
与傅里叶变换的方法相比,DMD方法无需在流场中精心布置监测点,仅通过流场快照即可得到剪切层K-H不稳定性的发生位置、宽频信号和模态特征等丰富的信息.当流场中剪切层的位置未知时(即非圆柱绕流流场时),DMD的这些优势将更为明显.此外DMD频率离散化的特点为fSL提供了一个更好的判断手段.
我们注意到,在目前的尾迹剪切层中,存在着由K-H不稳定性导致的涡旋尺度相近的DMD模态现象,为了更细致地分析该现象,尤其是小尺度流动的模态细节,今后有必要采用直接数值模拟的方法对该问题开展更深入的研究.
