70,73Ge的麦克斯韦平均截面计算
2021-09-02李雪黄美容王德鑫
李雪,黄美容,王德鑫
(1.内蒙古民族大学 数理学院,内蒙古 通辽028043;2.内蒙古民族大学 核物理研究所,内蒙古 通辽028043)
随着国防科技及核能与核技术研究的发展,近几年来新型核能系统的研发对核数据的需求越来越强烈,相关单位对核数据研究的关注度也逐渐加强,纷纷投入人力、物力开展核数据相关研究,进一步促进核数据研究工作的发展[1].
恒星中的重元素是通过不同机制产生的,如慢中子俘获(s过程)和快速中子俘获过程(r过程).在红巨星中发现的s过程解释了大约60%比56Fe重的原子核的起源,剩下的40%的原子核通常归因于r过程[2].其中麦克斯韦平均截面(Maxwell average cross section,简称MACS)是研究天体中重元素合成的重要参数,利用该参数可计算出太阳系的核素丰度、给出有关s过程中核合成的中子密度分布和宇宙年龄、温度等情况[3].因此,找到最适合的积分方式,对研究核天体物理起着重要作用.目前s过程核合成的计算通常基于专用的核天体物理数据库,如BAO等[4的工作.这些数据库包含麦克斯韦平均截面和天体物理反应速率的质量信息.NAKAGAWA等[5]也根据JENDL-3.3评价的核反应库计算了麦克斯韦平均截面和天体物理反应速率.
从20世纪40年代研究核数据开始,各个国家都先后建立了自己的评价核数据库,尤其是中子核数据库,并且不断地更新版本.比如美国的ENDF、欧洲的JEFF、日本的JENDL、中国的CENDL、前苏联的BROND等.美国国家核数据中心(NNDC)收录了ENDF/B-VII.1、JEFF-3.1.2、JENDL-4.0和CENDL-3.1[6-9]评价的核反应库的麦克斯韦平均截面和天体物理反应速率.笔者采用梯形数值积分、复化梯形积分、复化辛普森积分[10]对70Ge、73Ge(n,γ)的麦克斯韦平均截面进行计算,找到其中最合适的积分方法,并用该方法对ENDF/B-VIII.0、JEFF-3.3、CENDL-3.2和TENDL-2019[11-14]的最新版本的核反应库进行了计算.
1 麦克斯韦平均截面
设天体环境中有2种原子核x和y,其中y为靶核,x为入射炮弹,x和y发生核反应的反应速率与它们之间的相对运动速度v、反应截面σ以及A和B的数密度,即

其中,R为核反应的反应速率.
在天体环境中,核的速度分布可以用一个概率函数φ(v)表示,φ(v)满足[15]

因此,在计算时应该考虑到速度的分布,计算所有速度的平均值<σv>,即

其中,<σv>的含义是对每对核子的反应率.
总反应率可以表示为

为了使上述公式包含全同粒子的情况,通常把公式(4)改写成

核的数密度可以通过天体密度、核的质量分数或摩尔分数来计算

式中,NA是阿伏伽德罗常数,Ai是原子核i的质量.
通常,原子核运动速度遵从麦克斯韦-玻尔兹曼速度分布率,即

这里T是气体温度,m是原子核质量,指数项中的分子表示运动能量E=1/2mv2,函数φ(v)也可以写成能量E的函数

为了方便计算,通常温度以T6(106k)为单位,则温度和玻尔兹曼常数k的乘积kT可以转化为以keV单位的能量值,即kT=0.086 2×T6keV.对于发生在恒星介质内的核反应,参与反应的两个原子核x和y的速度分布都可以用麦克斯韦-玻尔兹曼分布描述.因此,每对原子核发生反应的速率,应该是两个速度分布的乘积的积
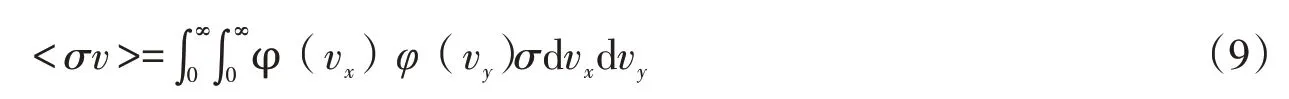
式中,v表示2个原子核之间的相对运动速度,用vx和vy分别表示核x与核y的运动速度.如果用V表示质心系运动速度:用μ表示x和y的约化质量,即μ=mxmy/(mx+my)总质量M=mx+my,则反应速率<σv>可以写成v与V的积分表达式
(10)式中,速度分布函数φ(V)和φ(v)分别表示为
和
由于速度分布函数φ(V)和φ(v)都是归一的,核反应界面仅与2个反应核之间的相对运动速度有关,因此式(10)可以简化为

将式(12)代入可得
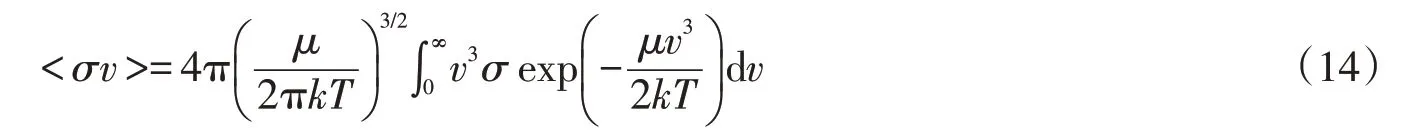
把速度v换成能量E后,上式可转化为
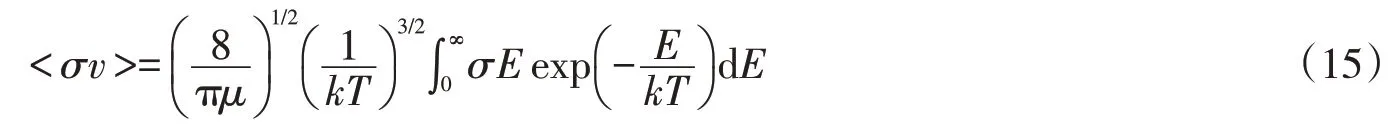
根据核天体物理反应率,将麦克斯韦的平均截面定义为

其中,v是中子和目标核素的相对速度,vt是平均热速度,由下式给出

由此得出麦克斯韦平均截面的计算公式为
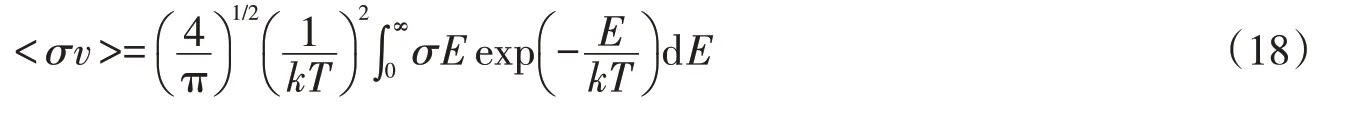
其中,k和T分别是系统的玻尔兹曼常数和温度,E是中子相对于目标的相对运动能量.ENDF-6格式横截面的值在实验室系统中制成表格,最后一个方程必须修改为[1]

其中,a=m2/(m1+m2),k和T分别是系统的玻尔兹曼常数和温度是实验室系统中的中子能量,m1和m2分别是中子和靶核的质量.
2 积分方法
2.1 梯形数值积分
与梯形积分不同,梯形数值积分(Trapezoidal numerical integration)是基于梯形积分形式改进的.通过梯形法执行数值积分运算.通过将一个区域分为包含多个更容易计算的区域的梯形,该方法对区间内的积分计算近似值.
当有一组数据Y时,通过梯形数值积分法计算Y的近似积分(采用单位间距),Y的大小确定求积分所沿用的维度:如果Y为向量,则梯形数值积分是Y的近似积分.如果Y为矩阵,则梯形数值积分对每列求积分并返回积分值的行向量.如果Y为多维数组,则梯形数值积分对其大小不等于1的第一个维度求积分.该维度的大小变为1,而其他维度的大小保持不变.
当有2组数据X、Y时,通过梯形数值积分法计算X、Y积分,根据X指定的坐标或标量间距对Y进行积分.如果X是坐标向量,则length(X)必须等于Y的大小不等于1的第一个维度的大小.如果X是标量间距,则梯形数值积分法对X,Y求积分等于X乘求积后的Y.
2.2 复化梯形积分
将区间[a,b]划分成N等分,子区间的长为,称hN为变步长.此时,节点为xk=x0+khN(k=0,1…,N).由定积分的性质和梯形公式,得到复化梯形公式为
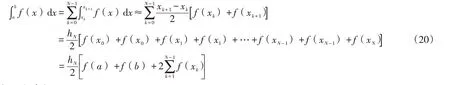
2.3 复化辛普森积分
将区间[a,b]划分成N等分,子区间的长为,在每个子区间上采取Simpson公式.此时,共有2N+1个节点.即,得到复化辛普森公式为
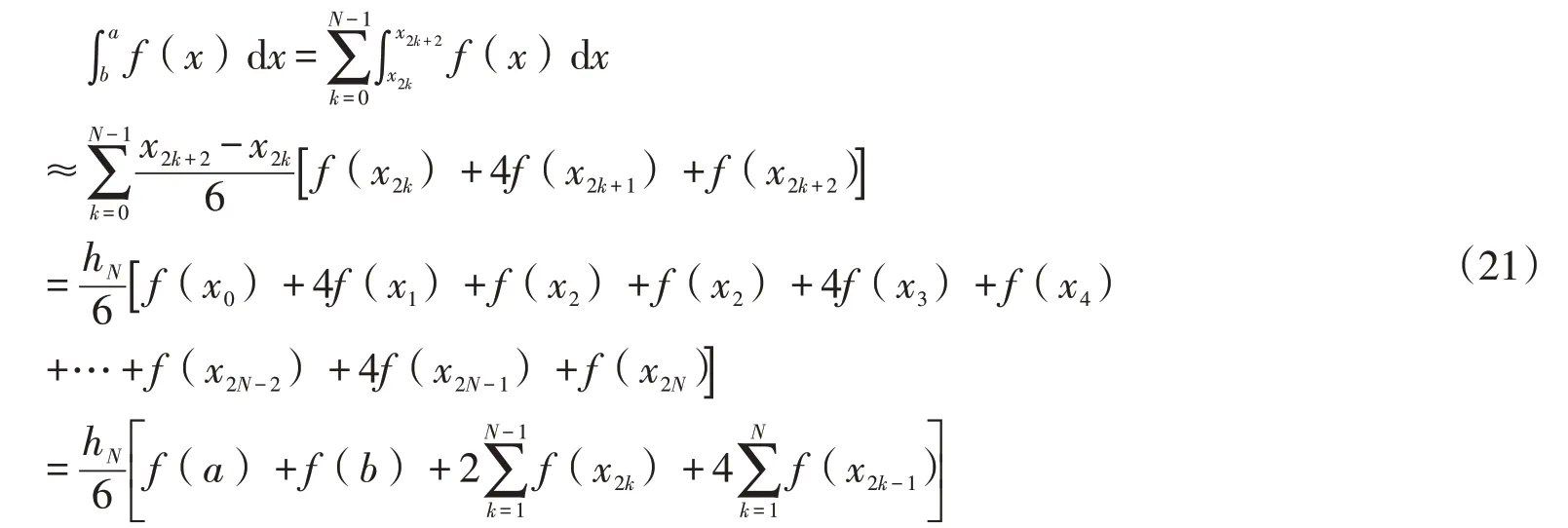
3 70Ge、73Ge的MACS计算
先前公布的麦克斯韦平均截面计算是基于线性化截面的辛普森积分法,笔者主要根据ENDF/BVII.1、JEFF-3.1.2、JENDL-4.0、CENDL-3.评价数据库查找的(n,γ)截面数据,运用梯形数值积分方法、复化梯形积分方法、复化辛普森积分方法对70Ge、73Ge在8~100 keV下的麦克斯韦平均截面进行计算,并与评价数据集Brookhaven National Laboratory report(BNL Report)[16]中数据进行对比,分析哪种积分方式计算结果更贴近于数据集BNL Report数据,接着用最合适的积分方式算出新评价数据库的麦克斯韦平均截面的值.
BNL Report计算了843种材料的中子截面、韦斯科特因子、共振积分、麦克斯韦平均截面和天体物理反应率.广泛分析新评价的中子反应截面、中子协方差和数据处理技术的改进促使研究者计算核工业和中子物理量,产生s过程麦克斯韦平均截面和天体物理反应率,系统地计算不确定性.讨论了核反应的计算结果,并给出了新的计算结果.因此计算结果与BNL Report对比是比较有可信度的.
3.1 70Ge的MACS计算
根据3种方法的计算结果与数据集BNL Report数据作图如下.
图1、图2、图3、图4分别为根据ENDF/B-VII.1、JEFF-3.1.2、JENDL-4.0、CENDL-3.1数据库计算的70Ge麦克斯韦平均截面与数据集BNL Report中麦克斯韦平均截面的对比图,其中Trapezoidal表示的是梯形数值积分方式的计算结果,Mulriple Trapezoidal表示的是复化梯形积分方式的计算结果,Mulriple Simpson表示的是复化辛普森积分方式的计算结果.从图1可以观察到梯形数值积分方式的计算结果除了在kT=40 keV时,略高于BNL Report数据,其他情况与BNL Report结果相符;复化梯形积分方式的计算结果与复化辛普森积分方式的计算结果相同,二者在kT=8~40 keV低于BNL Report的结果,在kT=50~100 keV处,3种计算方式所得结果相吻合.从图2可以观察到梯形数值积分方式的计算结果与BNL Report结果相一致,复化梯形积分方式的计算结果与复化辛普森积分方式的计算结果相契合.同样在kT=8~40 keV低于BNL Report,在kT=50~100 keV处,3种计算方式所得结果完全一致.图3所能观察到的与图1一样,梯形积分方式的计算结果与BNL Report结果符合的很好,除了在kT=40 keV时,略高于BNL Report数据;而复化梯形积分方式的计算结果与复化辛普森积分方式的计算结果是相吻合的,但是他们在kT=8~40 keV时低于BNL Report数据,但在kT=50~100 keV处,3种计算方式所得结果一致.图4的整个数据结果以及曲线走向都与前3个图有所不同,引起不同的原因是原始数据库截面数据的不同导致的,如图5所示.其次,可以观察到3种积分方式所得结果与BNL Report数据相差都很大,只有在kT=8~10 keV时梯形数值积分结果接近于数据库结果.
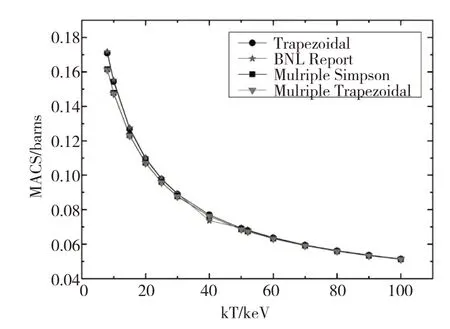
图1 ENDF/B-VII.1的麦克斯韦平均截面图Fig.1 Maxwell average cross section of ENDF/B-VII.1

图2 JEFF-3.1.2的麦克斯韦平均截面图Fig.2 Maxwell average cross section of JEFF-3.1.2
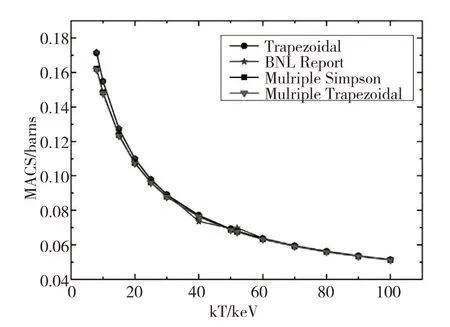
图3 JENDL-4.0的麦克斯韦平均截面图Fig.3 Maxwell average cross section of JENDL-4.0

图4 CENDL-3.1的麦克斯韦平均截面图Fig.4 Maxwell average cross section of CENDL-3.1
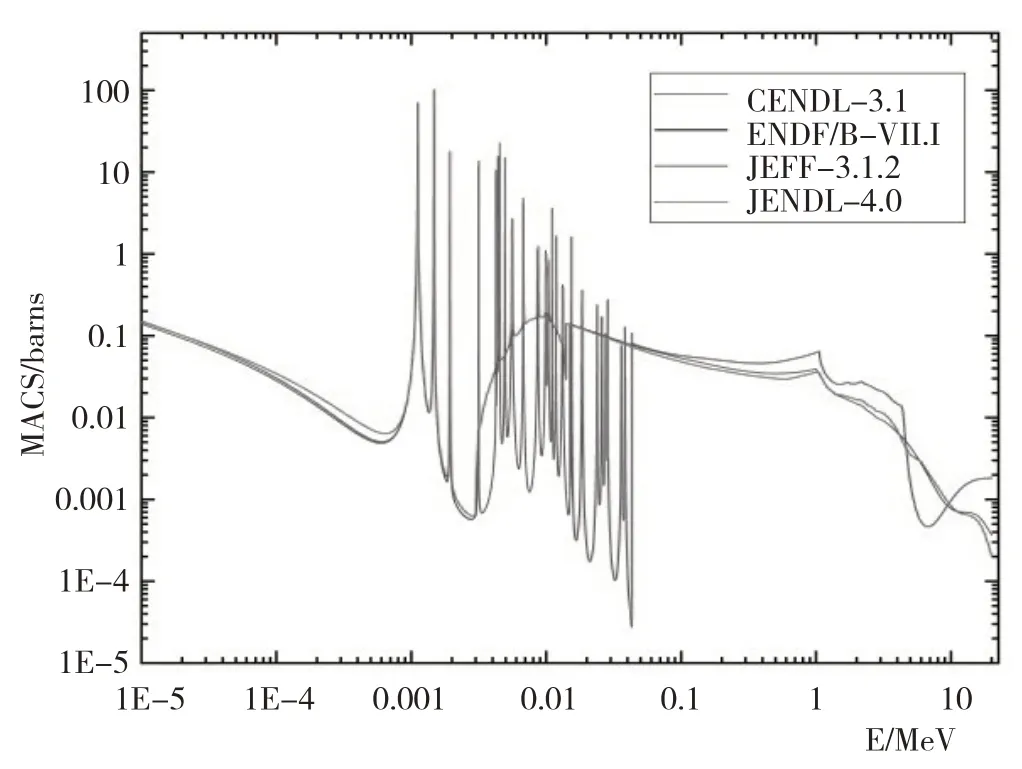
图5 7 0Ge不同数据库的(n,γ)截面数据对比图Fig.5 Comparison of(n,γ)cross section data of different70Ge databases
3.2 73Ge的MACS计算
根据3种方法的计算结果与数据集BNL Report数据作图如下.
图6、图7、图8、图9分别为根据JEFF-3.1.2、ENDF/B-VII.1、CENDL-3.1、JENDL-4.0、数据库计算的73Ge麦克斯韦平均截面与数据集ENL Report中麦克斯韦平均截面的对比图.从图6可以观察到梯形积分方式的计算结果在kT=8~60 keV时略高于BNL Report数据,而在60 keV之后两者吻合;而复化梯形积分方式的计算结果与复化辛普森积分方式的计算结果是一致的,但是它们在kT=8~60 keV时低于BNL Report数据,但在kT=60~100 keV处,3种计算方式所得结果一致.从图7可以观察到梯形数值积分方式的计算结果与BNL Report数据相同,复化梯形积分方式的计算结果与复化辛普森积分方式的计算结果很吻合,同样在kT=8~60 keV时低于BNL Report数据,在kT=60~100 keV处,3种计算方式所得结果符合的很好.图8所能观察到梯形数值积分方式的计算结果稍高于BNL Report数据;而复化梯形数值积分方式的计算结果与复化辛普森积分方式的计算结果相符,但是它们在kT=8~60 keV处低于BNL Report数据,但在kT=60~100 keV处,3种计算方式所得结果一致.由图9可以看出在kT=8~60 keV处,梯形数值积分结果高于BNL Report数据,复化梯形积分方式的计算结果与复化辛普森积分方式的计算结果低于BNL Report数据.

图6 ENDF/B-VII.1的麦克斯韦平均截面图Fig.6 Maxwell average cross section of ENDF/B-VII.1
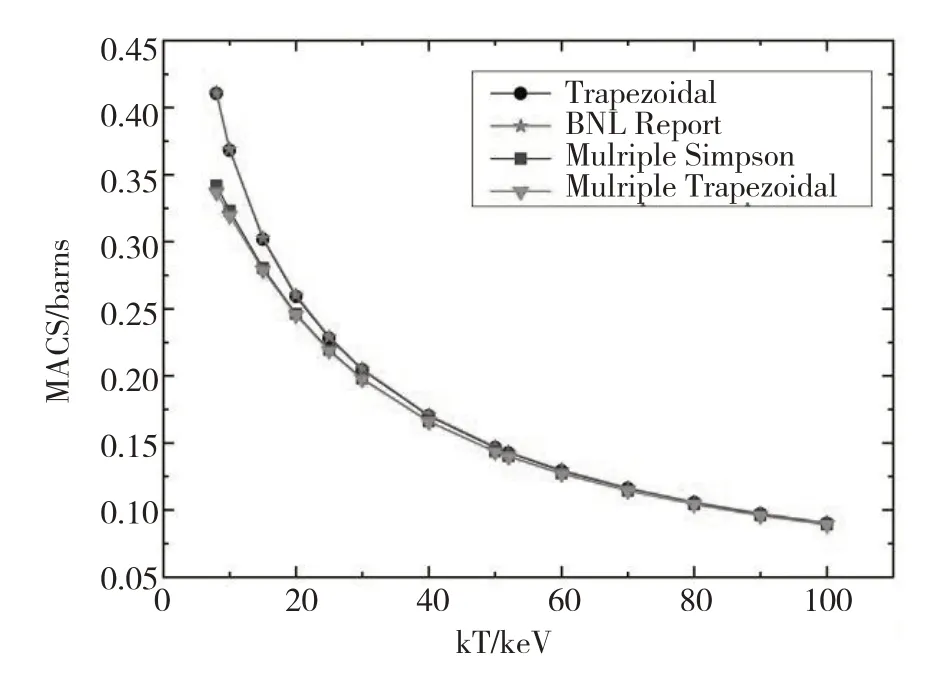
图7 JEFF-3.1.2的麦克斯韦平均截面图Fig.7 Maxwell average cross section of JEFF-3.1.2

图8 CENDL-3.1的麦克斯韦平均截面图Fig.8 Maxwell average cross section of CENDL-3.1
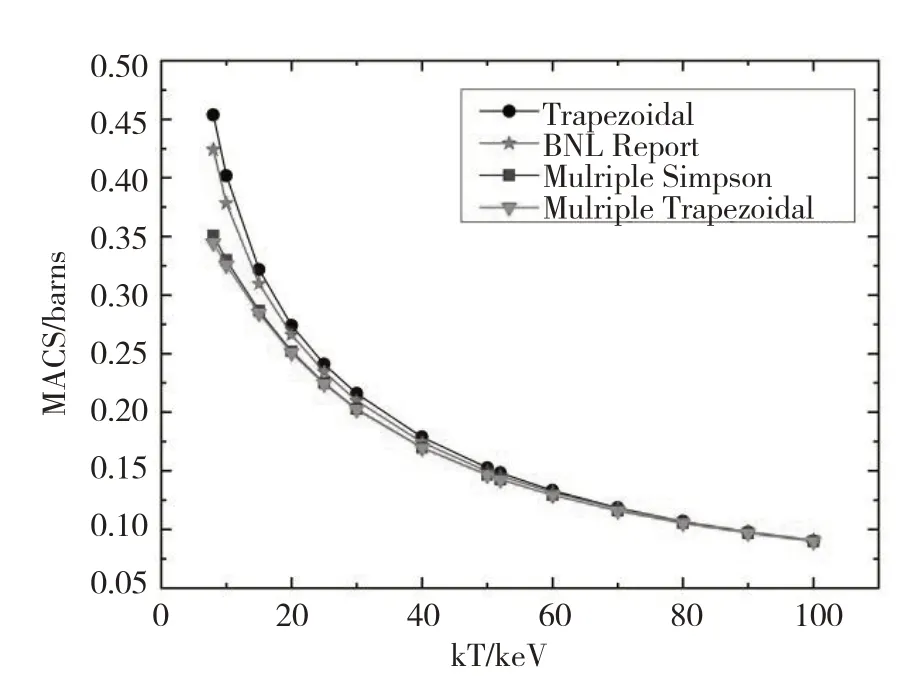
图9 JENDL-4.0的麦克斯韦平均截面图Fig.9 Maxwell average cross section of JENDL-4.0
3.3 70Ge、73Ge在ENDF/B-VIII.0、CENDL-3.2、JEFF-3.3、TENDL-2019数据库下的MACS计算
根据不同评价的核反应数据库分别用梯形数值积分、复化梯形积分、复化辛普森积分对70Ge、73Ge计算恒星核合成反应(n,γ)的麦克斯韦平均截面结果与BNL Report提供的麦克斯韦平均截面数据进行比较,结果发现用梯形数值积分的积分结果最为符合.所以运用相同方法计算了新的评价数据库的麦克斯韦平均截面.
运用梯形数值积分方法,计算新的评价数据库ENDF/B-VIII.0、CENDL-3.2、JEFF-3.3、TENDL-2019的麦克斯韦平均截面.结果如下.
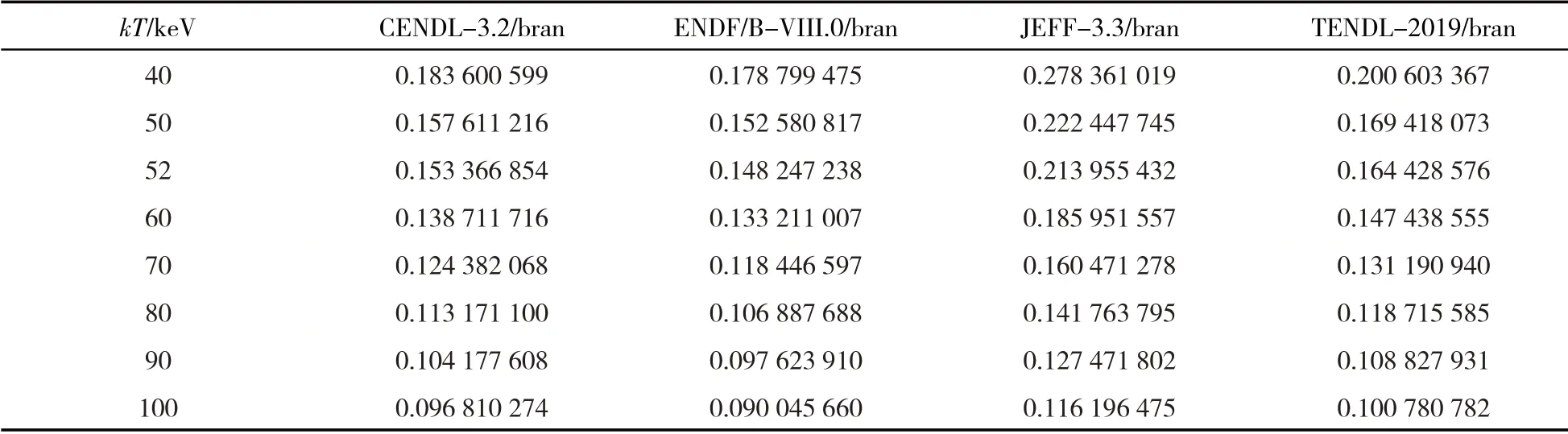
续表2
从表1、表2可以看出,无论是70Ge还是73Ge,对于ENDF库、CENDL库新旧版本(n,γ)截面数据计算结果差距不大,CENDL、JEFF-3.3新的数据库数据,与原版本有一点差别,原因在于数据库原始截面数据的差异.就总体而言,几乎没有变化.通过数据,观察到JEFF库的变化很大,所以对新旧数据库的(n,γ)截面数据进行了比较.如图10、图11,发现数据库的变化很大,对麦克斯韦平均截面的影响较大,所以对新的(n,γ)截面数据进行计算是非常必要的.
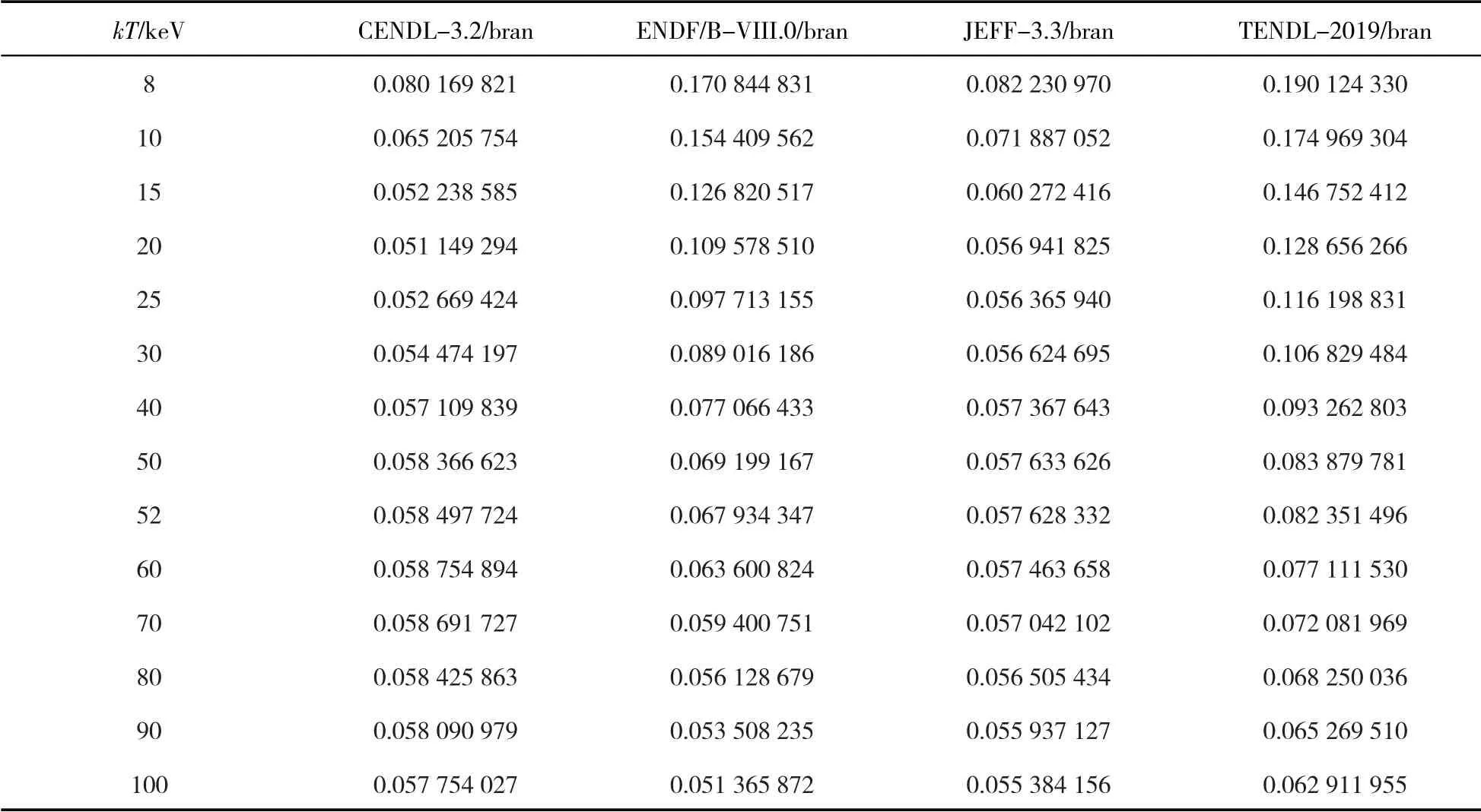
表1 ENDF/B-VIII.0、CENDL-3.2、JEFF-3.3、TENDL-2019评价数据库截面数据用梯形数值积分方式所得7 0Ge的麦克斯韦平均截面Tab.1 ENDF/B-VIII.0,CENDL-3.2,JEFF-3.3,TENDL-2019 evaluation database cross section data using trapezoidal numerical integration method to obtain the Maxwell average cross section of70Ge

表2 ENDF/B-VIII.0、CENDL-3.2、JEFF-3.3、TENDL-2019不同评价数据库截面数据用梯形数值积分方式所得7 3Ge的麦克斯韦平均截面数据Tab.2 ENDF/B-VIII.0,CENDL-3.2,JEFF-3.3,TENDL-2019 different evaluation database cross section data using trapezoidal numerical integration method to obtain the Maxwell average cross section data of73Ge
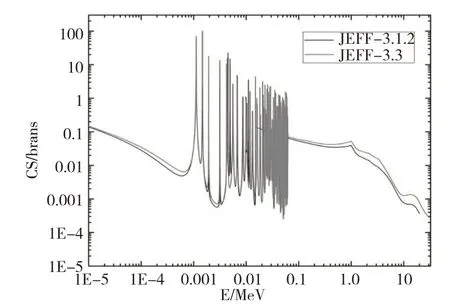
图10 70Ge JEFF新旧数据库的(n,γ)截面数据对比图Fig.10 Comparison of(n,γ)cross section data of 70Ge JEFF old and new databases
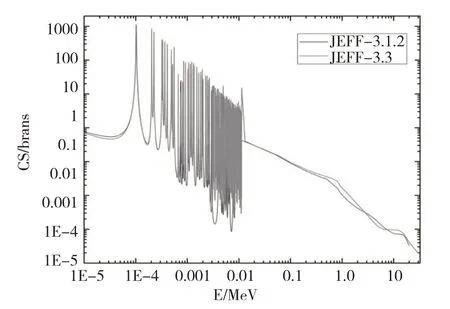
图11 7 3Ge JEFF新旧数据库的(n,γ)截面数据对比图Fig.11 Comparison of(n,γ)cross section data of 73Ge JEFF old and new databases
4 结语
核数据是用来描述原子核基本性质、核衰变以及入射粒子与原子核发生反应过程等方面信息的统称,是核科学与核工程应用所需的重要基础数据,其精度和可靠性直接关系着核工程产品的可靠性、安全性和经济性.其中麦克斯韦平均截面的精度及准确性对于现阶段的研究也是非常重要的,因此,通过不同评价的核反应数据库分别用梯形积分、复化梯形积分、复化辛普森积分对70Ge、73Ge计算恒星核合成反应(n,γ)的麦克斯韦平均截面进行了计算,发现梯形数值积分方法所得结果最为符合,对接下来计算各种核反应参数是有极大帮助的,同时也希望能为其他研究者提供参考.
