玻璃细集料混凝土柱的抗震性能有限元分析

王凤池*，郭昊，胡海明2，张雨石

(1.沈阳建筑大学 土木工程学院， 辽宁 沈阳 110168;2.沈阳建筑大学图书馆， 辽宁 沈阳 110168)

0 引言

自20世纪60年代以来，玻璃废弃物所产生的一系列不利影响逐渐浮现，对环境及社会造成了严重危害，如闪色污染、土地资源浪费等。SHAO等[1-2]，分别研究了废弃玻璃粉、碎玻璃对部分水泥和粗骨料替代的可行性，其结果表明玻璃集料混凝土满足混凝土的基本使用要求；FABIO等[3- 4]研究表明当掺入偏高岭土或控制玻璃粒径小于1mm时，能够抑制玻璃颗粒引起的碱骨料反应；ELAQRA等[5]研究了玻璃粉与其他混凝土材料混合前，在水中浸泡的时间对混凝土硬化性能的影响；KIM等[6]研究了以玻璃砂替代细骨料的玻璃集料混凝土，在抗冻融循环、硫酸盐侵蚀及氯离子渗透等方面的性能；王凤池等[7]研究了在不同玻璃骨料质量取代率下混凝土抗压强度变化规律；杨凤玲等[8-9]研究了玻璃骨料粒径对废弃玻璃骨料混凝土的强度和变形性能的影响。

针对玻璃骨料混凝土柱的研究，主要集中于静力试验方面，如NIANG等[10]对掺入玻璃砂的钢筋混凝土柱进行了结构性能研究；王凤池等[11]研究了玻璃混凝土长柱的偏心受压性能。综上可知，对于玻璃骨料混凝土柱抗震性能方面的研究相对匮乏。因此，本文通过运用ABAQUS有限元分析软件，研究了玻璃骨料替代率、长细比、轴压比和偏心距对玻璃混凝土柱抗震性能的影响，不仅克服了以实验手段研究参数变化影响过程中，因试件数目繁多而给实验带来的困难，也可为玻璃混骨料凝土柱的拟静力试验提供参考，为玻璃混凝土柱的设计提供依据。

1 有限元模型的建立

1.1 材料的本构关系

选用合适的本构关系是模型建立的基础。普通混凝土本构关系，采用《混凝土设计规范》(GB 50010—2010)[16]推荐的应力-应变曲线模型，如图1所示。玻璃骨料混凝土本构关系，采用文献[11]中提出的玻璃集料混凝土长柱受压本构模型；钢筋选用了双折线随动强化模型，本构关系如2图所示。

图1 混凝土单轴应力-应变曲线Fig.1 Concrete under uniaxial stress-strain curve

图2 钢筋的应力-应变曲线Fig.2 Stress strain curve of rebar

1.2 模型构建设计

通过ABAQUS有限元分析软件创建21组玻璃集料混凝土柱的实体模型，探究低周反复荷载作用下细骨料替代率、长细比、轴压比和偏心距等参数对玻璃混凝土柱抗震性能的影响。构件外形采用矩形截面牛腿柱，截面尺寸200 mm×200 mm。为避免发生构件发生局压破坏，上、下柱端部各设置18 mm厚的刚性垫片，且刚性垫片与柱端采用绑定约束。试件尺寸及钢筋布置详图如图3所示。

图3 试件配筋图Fig.3 Specimen reinforcement diagram

混凝土强度等级设计为C30；玻璃细骨料的参数设定采用试验实测值，如细骨料最大粒径2.5 mm、细度模数为2.97，属于中砂、Ⅱ级级配、表观密度为2 500 kg/m3；纵筋选择直径12 mm的HRB400级钢筋，箍筋选用直径为8 mm的HPB235级钢筋。钢筋及混凝土的力学参数见表1及表2,试件的基本参数见表3。

垫板与玻璃集料混凝土均采用八节点缩减积分三维实体单元 (C3D8R)，纵筋与箍筋选用两节点线性三维桁架单元 (T3D2)。网格划分对有限元软件的计算结果有着重大的影响，经反复计算和调整，玻璃混凝土与钢筋的全局种子尺寸设定为20 mm。

表1 钢筋的力学性能Tab.1 Mechanical properties of steel bars

表2 混凝土的力学性能指标Tab.2 Mechanics performance of concrete

表3 试件的基本参数Tab.3 Basic parameters of the specimen

图4 位移加载图Fig.4 Displacement loading map

1.3 边界条件及加载方法

构件的边界条件设定与试验保持一致，下柱端对X、Y、Z三个方向的水平及转动自由度进行约束，上柱端锁定X、Y、Z三方向的转动自由度。为模拟真实试验加载过程，加载方式由两个分析步组成：第一步，柱顶垫板处施加恒定竖向集中荷载；第二步，柱顶侧面加载点施加位移控制的水平反复荷载作用。位移加载如图4所示。

2 有限元计算结果分析

2.1 滞回曲线

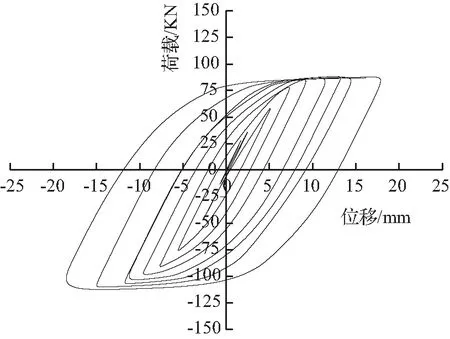
图5为100%骨料替代下各构件的滞回曲线。滞回曲线即反复荷载作用下构件的荷载-位移曲线，其可反映结构在受力过程中的耗能、承载力及刚度退化等抗震性能。不同骨料替代率下，各构件滞回曲线的变化特征相同，因此，本文以100%骨料替代下各构件的滞回曲线为例进行分析。

由图5分析可知，各构件的滞回曲线均呈梭形且较为饱满，无捏缩现象，均具有较好的抗震性能。加载初期，各构件处于弹性阶段，P-Δ曲线呈线性，耗能较少；随控制位移的增加，构件逐渐屈服，进入弹塑性阶段，P-Δ关系呈非线性发展，曲线斜率渐向位移轴倾斜，滞回环愈加饱满，耗能增强，且卸载后残余变形愈加明显；构件变形达到峰值位移时，构件发生极限破坏，峰值荷载不随加载增加而发生明显变化，但各构件的变形明显加快，残余变形更加显著。

对比分析图5(a)、图5(b)、图5(c)可知，随长细比增加，水平承载力峰值减小，长细比为0.4时，水平承载力峰值最大；滞回曲线饱满度呈先增后减趋势，长细比为0.5时，滞回曲线饱满程度最高，能量耗散最多。

对比分析图5(b)、图5(c)、图5(d)可知，随轴压比增大，各构件承载力无显著变化，滞回曲线饱满度呈先减后增趋势，长细比为0.2时，滞回曲线饱满程度最高。

对比分析图5(b)、图5(e)、图5(g)可知，随偏心距增大，滞回曲线均较为饱满且整体向下偏移，抗拉承载力下降，抗压承载力上升。

(a) PB1

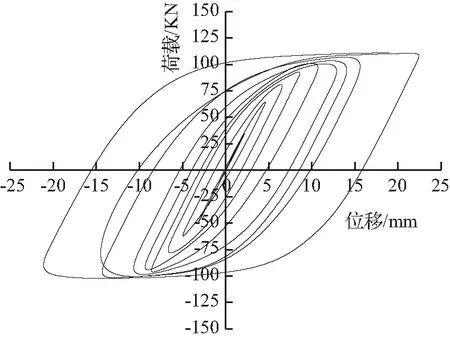
(b) PB2

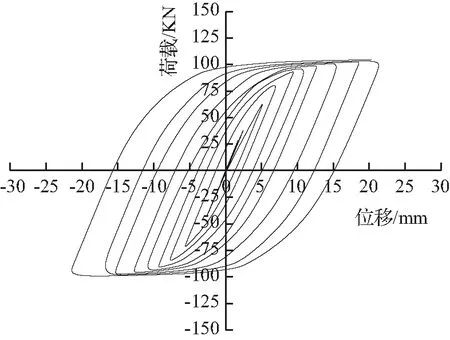
(c) PB3

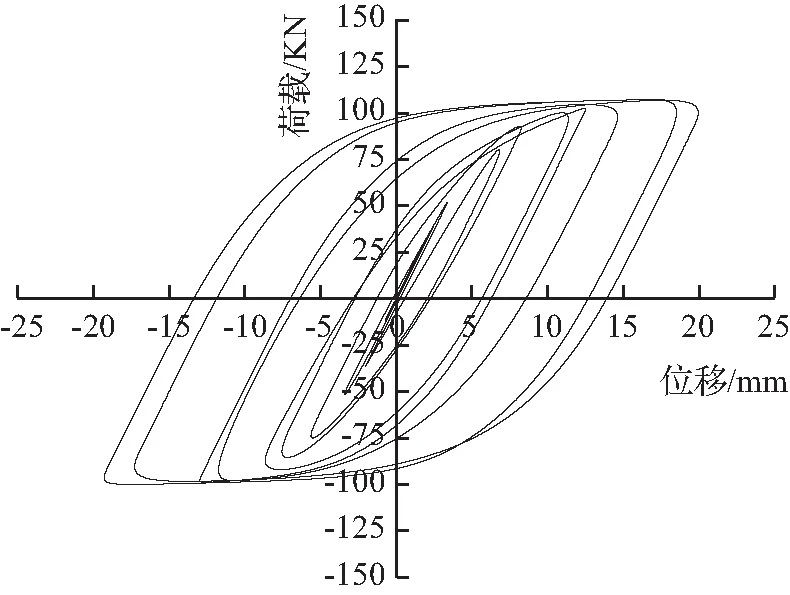
(d) PB4

(e) PB5

(f) PB6

(g) PB7

2.2 骨架曲线

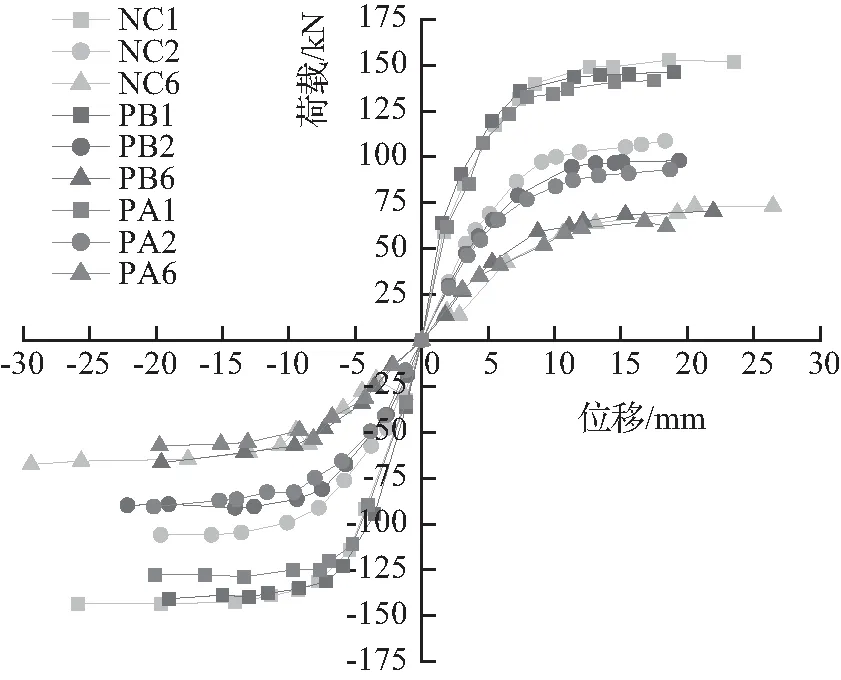
每级滞回循环的荷载峰值点连接所得包络曲线为滞回循环骨架曲线，各构件的骨架曲线如图6所示。

由图6(a)可知，长细比对不同替代率下各构件的抗震性能影响较大，随长细比增加，试件初始刚度、极限位移值及屈服荷载均明显下降。其主要原因在于，长细比增加，导致轴向力在构建内部产生较大的附加弯矩，降低了构件的水平承载力；同一长细比中，100%骨料替代构件与对照组的骨架曲线基本重合。

由图6(b)可知，各骨架曲线分布较为集中且无明显差异，由此可知，轴压比对构件的骨架曲线变化无明显影响；

由图6(c)可知，随偏心距的增大，构件的刚度、受拉承载力及延性性能均有明显降低；初始偏心距为0时，50%骨料替代下构件的骨架曲线性能最差。

对比分析图6可知，100%骨料替代下构件的抗震性能与对照组构件相近，且优于50%骨料替代下构件的抗震性能，其原因在于，细骨料取代率为50%时，由于玻璃的材料性质与自然砂石不同，因此玻璃细骨料和砂子间的黏结性能较差，导致两者协同工作能力较低，从而影响了构件的抗震性能。

(a) 长细比影响对比图

(b) 轴压比影响对比图

(c) 偏心距影响对比图

2.3 承载力及延性性能

各试件的荷载特征值、位移值及延性系数见表4。表4中Δy与Δu分别代表屈服荷载Py和极限荷载Pu的对应位移值，其中Py可通过“几何作图法”确定，Pu取峰值荷载下降到85%时的对应值；延性系数μ可由公式：μ=Δu/Δy计算得出。

表4 构件骨架曲线特征点荷载及侧移值Tab.4 Component skeleton curve feature point load and lateral shift value

分析表4可知，以长细比为4时，各试验组的屈服荷载及极限荷载分别作为标准值，则当长细比为5时，不同骨料替代率下构件的各荷载特征值约为标准值的69%～72%，长细比为6时，约为标准值的40%～47%，因此不同替代率下，长细比对各构件的承载力有显著影响，随长细比的增加，构件的承载力明显下降。偏心距的增加对普通混凝土构件无显著影响，但对玻璃混凝土构件影响较为明显。此外，PA7构件较PA3构件的极限荷载下降5.1%，PB5构件较PB3构件下降7.5%，PB7构件较PB3构件下降11.2%，经对比后可知：随偏心距的增加，玻璃混凝土构件的荷载特征值均小幅下降，但偏心距为0时，100%骨料替代下构件的承载力略高于普通混凝土构件。轴压比对构建的承载力无显著影响。

分析表4可知，替代率为0时，各构件的延性系数在2.63～4.26；替代率为50%时，构件的延性系数在2.56～3.8间；替代率为100%时，延性系数在2.61～3.86。当排除各替代率中长细比为6的构件时，100%骨料替代构件和0替代构件的延性系数均≥3，由此可知，长细比为6时，各构件的延性性能最差，当长细比≤5时，各构件的延性良好。轴压比对普通混凝土延性系数无显著影响，但对玻璃混凝土影响较大，随轴压比增加，玻璃骨料混凝土延性系数均呈先减后增趋势，当轴压比=0.6时，其延性系数最大。当其他变量参数相同时，100%骨料替代构件的延性系数较对照组下降<5%，而50%骨料替代构件约下降13%。

图7 计算简图Fig.7 Schematic diagram of equivalent viscous damping coefficient calculation

由表4知，在不同骨料替代率中，当长细比为4、偏心距为0且轴压比为0.2时，构件的各荷载特征值达到最大值。当以NC1的荷载特征值分别作为标准值时，PA1的屈服强度及极限强度约为标准值的91%，PB1的各荷载特征值约为标准值的96.9%。

综上可知，骨料替代率达到100%时，构件具有良好的延性性能，且荷载特征值与对照组构件无明显差异。

2.4 耗能性能

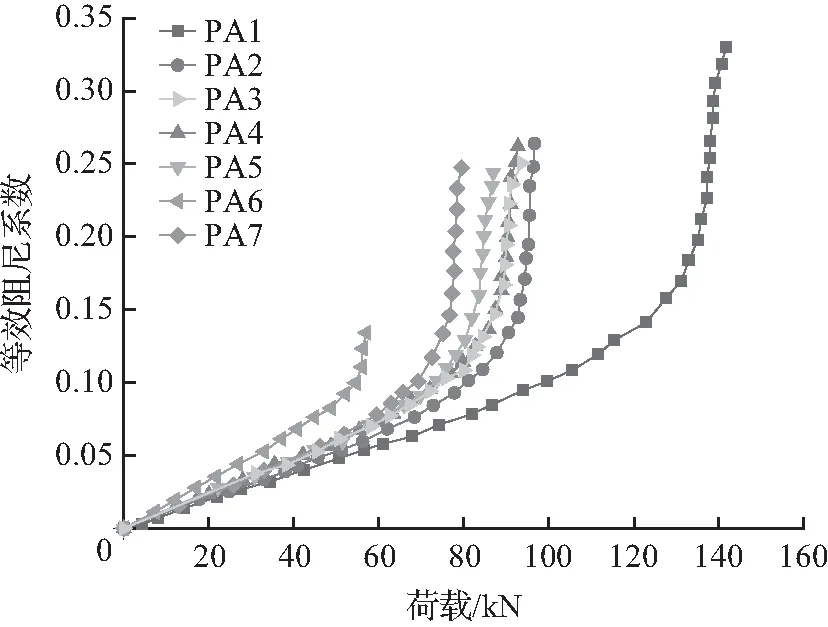
耗能能力，即地震作用下结构或构件通过变形耗散能量的能力，工程上常以等效黏滞阻尼系数对其进行评价。各构件等效黏滞阻尼系数he由下述公式(1)计算所得，计算简图如图7所示，计算结果见表5。等效黏滞阻尼系数变化曲线如图8所示。

(1)

通过对表5与图8对比分析可知，加载前期，等效黏滞阻尼系数曲线呈线性，增势平缓；加载至构件屈服后，等效黏滞阻尼系数迅速增长，曲线斜率陡增。这是由于，构件屈服前，残余变形较小且发展较慢；构件屈服后，残余变形发展迅速，能量耗散显著提升。因此表明，各构件的耗能能力，随其变形的增大逐渐增强。

分析图8可知，长细比对构件耗能影响显著，在各骨料替代率的试验组中，长细比为4时各荷载特征点的等效阻尼系数值均保持最大，长细比为6时最小，说明随长细比增加，等效阻尼系数显著下降。此外，随轴压比增大，等效阻尼系数值呈小幅下降趋势，与之相比，偏心距对构件的耗能能力无明显影响。

由表5可知，若以自然集料混凝土构件的等效黏滞阻尼系数作为标准值，则骨料替代率为50%时，各构件的等效黏滞阻尼系数较标准值下降0.02～0.04，骨料替代率为100%时，各构件较标准值下降0.01～0.02；以普通混凝土构件的耗能作为标准值，则50%骨料替代下各构件较标准值下降100～200 kN·mm，全骨料替代下各构件较标准值约提升200 kN·mm。由此可知，玻璃混凝土柱与普通混凝土柱的耗能能力相近，且替代率为100%时玻璃混凝土柱的耗能最优。

(a) 自然集料构件组

(b) 50 %玻璃集料构件组

(c) 100 %玻璃集料构件组

2.5 刚度退化

刚度退化，即反复荷载作用下，随加载位移的增加，构件刚度因累计损伤而导致不断下降的现象。本文采用环线刚度Ki变化，以反映各构件的刚度退化情况，环线刚度计算公式(2)如下。构件刚度退化曲线如图9所示。

(2)

分析图9可知，各构件刚度变化趋势一致，随加载位移的增加，前期刚度变化曲线下降明显，后期曲线逐渐趋于平缓；部分构件加载位移初期，刚度出现小幅波动，这是由加载初期构件的刚度大，但加载唯一小所致。

(a) 50 %玻璃集料构件组

(b) 100 %玻璃集料构件组

(c) 自然集料构件组

加载初始，玻璃混凝土构件刚度较高于普通混凝土；随加载位移增加，构件刚度呈下降趋势，且玻璃混凝土曲线斜率大于普通混凝土，致使构件屈服后，普通混凝土构件刚度开始反超玻璃混凝土。因此，普通混凝土构件刚度退化程度略小于玻璃混凝土，但差异不明显。

3 结论

通过玻璃集料混凝土柱拟静力试验的有限元模拟，以及对模拟结果的分析，可得出以下结论：

① 低周反复荷载作用下，21种不同类型混凝土柱构件的滞回曲线均呈梭形，饱满度较好；无初始偏心条件下，长细比=4、轴压比=0.2时，玻璃集料混凝土和自然集料混凝土构件的黏滞阻尼系数均>0.3，说明在该条件下玻璃混凝土具有良好的耗能能力。

② 长细比对构件的抗震性能影响较为显著，随长细比的增大，构件的刚度、水平承载力、耗能及延性性能均大幅降低；轴压比对各构件抗震性能影响较小，随轴压比增加，构件承载力无明显变化，能量耗散呈小幅下降趋势，在较高轴压比下，各构件的抗震能力较好；随偏心距的增大，废弃玻璃混凝凝土柱的抗拉承载力减小，抗压承载力增大，初始偏心距=0时，其性能最优。

③ 100%骨料替代下玻璃集料混凝土柱的抗震性能良好，与自然集料混凝土构件性能相近，优于50%骨料替代下的玻璃混凝土构件；在无初始偏心下，长细比=4、轴压比=0.2时，100%骨料替代下构件的耗能能力略大于普通混凝土构件。由此可知，100%骨料替代下玻璃混凝土柱已满足工程抗震性能要求，可用于实际工程。