锤头曲率半径对RC梁抗冲击性能影响
2021-09-01
(1.桂林理工大学 土木与建筑工程学院, 广西 桂林 541004;2.广西建工轨道装配式建筑产业有限公司, 广西 柳州 545000)
0 引 言
钢筋混凝土(reinforced concrete, RC)结构在其生命周期中难免会遇到极端荷载的影响,对结构造成不可挽回的重大损坏,使其彻底丧失正常使用功能。而建筑结构中梁作为重要受力构件,在遭受冲击荷载时,其冲击动态响应在很大程度上将影响建筑结构整体的安全性能。由于冲击荷载的作用时间短、破坏性强、加载速率快,构件在冲击荷载作用下会表现出与静力加载作用时截然不同的特性。迄今为止,已经进行了一些试验[1]和数值模拟[2]来研究冲击荷载作用下RC梁的动力响应。
何庆锋等[3]通过对叠合梁以及采用碳纤维布加固梁进行落锤冲击试验,研究表明:后浇叠合面在一定程度上抑制了跨中裂缝向上开展的趋势,具有较好的抗冲击性能。许斌等[4]对不同配筋的RC梁进行了静力加载与冲击试验,研究表明:梁延性越好,其抗冲击能力越强。PHAM等[5]通过试验和数值模拟的方式,证明落锤与RC梁之间接触刚度的变化对作用在梁上的冲击力有很大影响。但在以往的大多数试验研究中,不同的试验采用的锤头曲率半径各不相同[6- 8]。
虽然已经知道不同落锤曲率半径对RC梁抗冲击性能具有较大影响。但是对落锤曲率半径的系统研究尚未见报道。因此,有必要开展系统研究,量化落锤头曲率半径对RC梁冲击性能的影响,从而得出RC梁在冲击荷载作用下的响应特性。本次研究使用ANSYS/LS-DYNA有限元软件对RC梁进行冲击荷载下的数值模拟,研究锤头曲率半径对RC梁抗冲击性能的影响。
1 混凝土梁有限元模型建立
1.1 试验简介
FUJIKAKE等[9]对3种配筋率共12根RC梁进行冲击试验。其中梁总长1 700 mm,支座两点间的距离为1 400 mm,截面尺寸为150 mm×250 mm。试验采用配筋方式[9]如图1所示,不同试件配筋情况[9]见表1。

图1 试件原型图Fig.1 Sample prototype diagram

表1 试件配筋情况Tab.1 Table of reinforcement for specimens
图2为试验加载装置,将质量为400 kg的落锤从4种不同高度自由下落击中跨中RC梁的顶面;S1322系列和S2222系列梁试件对应落锤高度分别为0.30、0.60、1.20、2.40 m;S1616系列梁试件对应落锤高度为0.15、0.30、0.60、1.20 m。锤头为一个半径为90 mm的半球。锤头和RC梁之间的冲击力通过固定在落锤上的荷载传感器测量[9]。
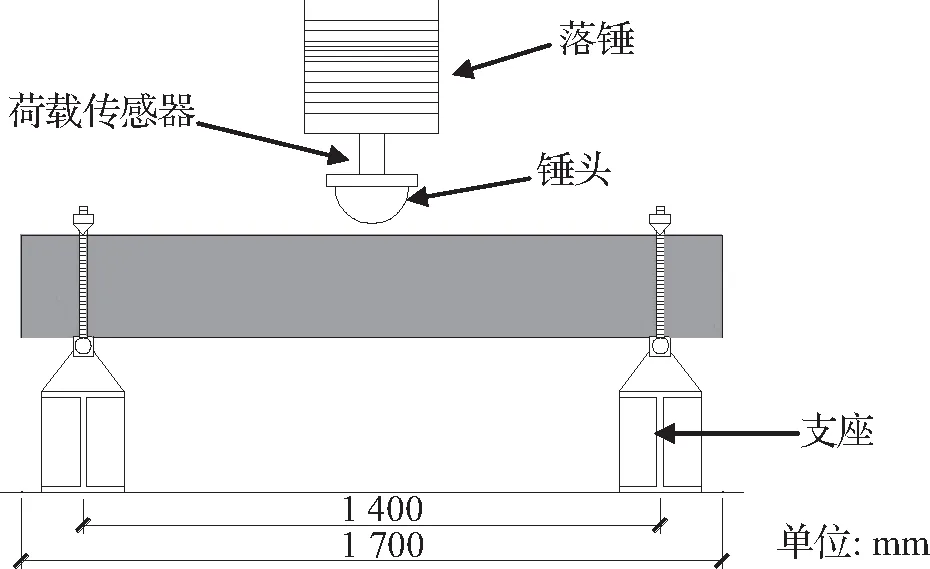
图2 冲击加载试验装置Fig.2 Drop-weight test device Schematic diagram
1.2 有限元模型建立
本次有限元分析选用高精度商用有限元软件ANSYS/LS-DYNA进行建模和计算。前期研究[10-12]已经证明商用有限元软件可以非常好的对碰撞、冲击等问题进行预测。
1.1.1 单元类型选取
混凝土采用SOLID164三维实体单元建模,同时采用单点积分算法。钢筋采用BEAM161梁单元建模,该单元能够模拟轴向拉压、双轴弯曲和有限应变,常用于模拟钢筋[13]。
1.2.2 材料模型选取
混凝土所采用的材料本构模型为*MAT_CSCM_CONCRETE (MAT_159),其本构模型的特点是结合最大主应变破坏准则的应用,可以有效地模拟冲击荷载作用下混凝土本构及RC结构的破坏模式[14]。为考虑在冲击荷载作用下混凝土的应变率,此处需要打开本构模型中控制应变效应的关键字功能,即IRATE设定为1,其余参数根据CSCM用户手册[15]中介绍的fc和Ag确定。钢筋所采用的材料本构模型为*MAT_PLASTIC_KINEMATIC (MAT_003),其本构模型关系为双线性。为考虑冲击荷载下的钢筋材料本构关系,对本构模型中SRC和SRP两参数根据Cowper-Symonds模型进行设定。两种材料模型所需输入的参数均为文献[9]计算所得。
1.2.3 模型确立
采用ANSYS/LS-DYNA建模得到的RC梁精细化有限元模型如图3所示。为了贴合试验真实情况,并提高求解效率,对边界条件进行一定的简化。将试验中的支座简化为约束x、y、z方向上平动位移的钢轴,落锤简化为约束x、z方向上平动位移的刚体。并使用关键字*CONTACT_AUTOMATIC_SINGLE_SURFACE实现支座及落锤与RC梁的接触。

图3 混凝土梁有限元模型Fig.3 RC beam finite element model
2 模型验证
2.1 冲击力时程曲线对比
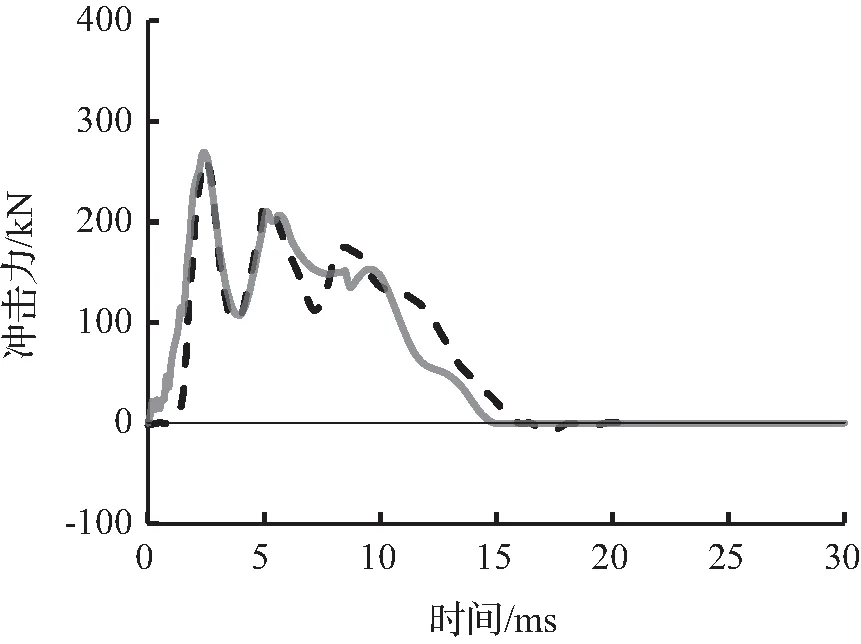
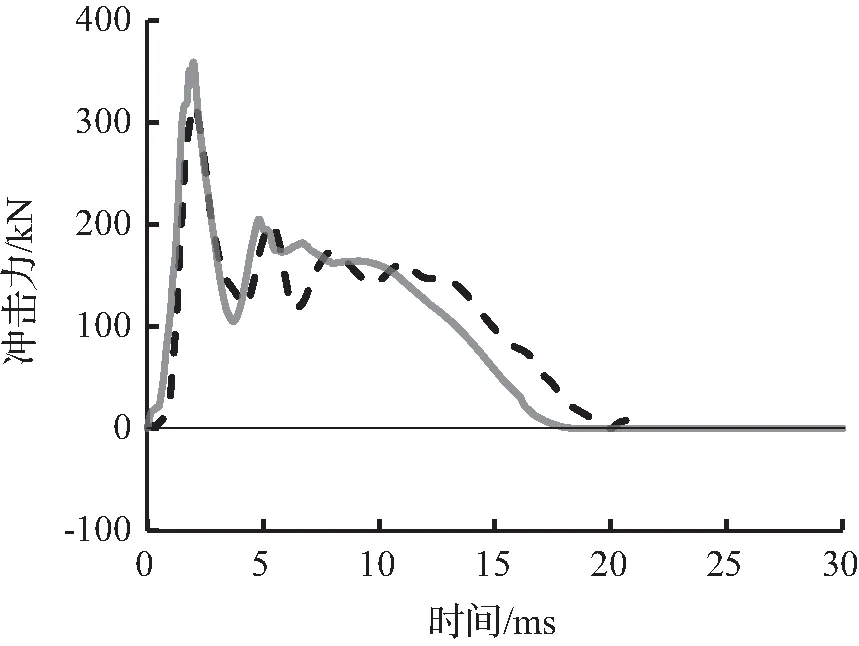
图5至图7为有限元模拟预测的冲击力时程曲线与试验冲击力时程曲线结果对比。从图6可以看出有限元模拟所预测的冲击力时程曲线与试验冲击力时程曲线吻合较好,变化趋势接近。
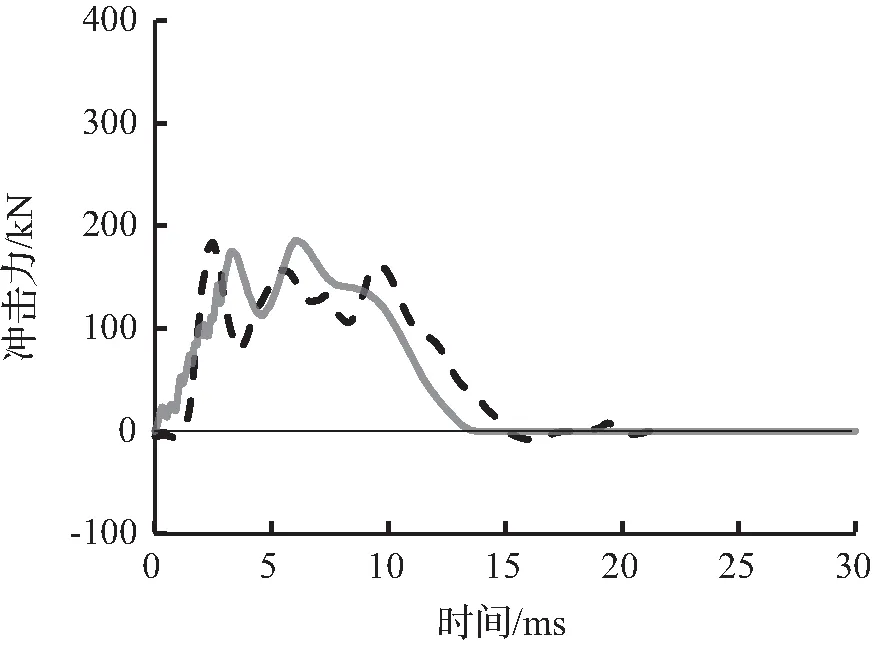
(a) 0.30 m

(b) 0.60 m
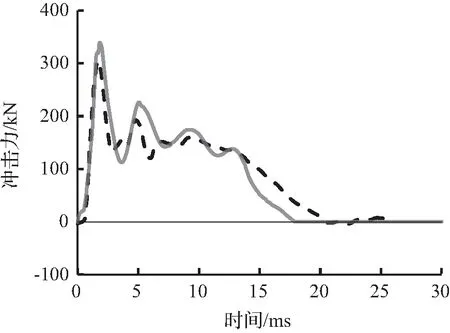
(c) 1.20 m
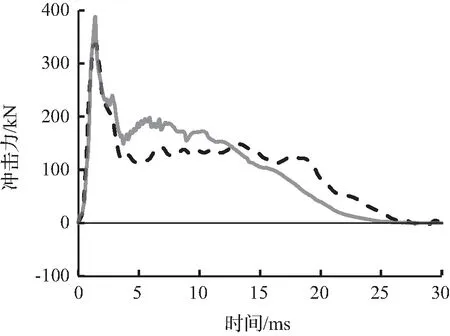
(d) 2.40 m

图5 S1322冲击力时程曲线对比Fig.5 Comparison of impact force time history curves for S1322
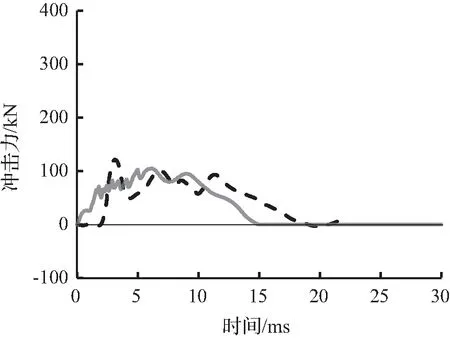
(a) 0.15 m

(b) 0.30 m
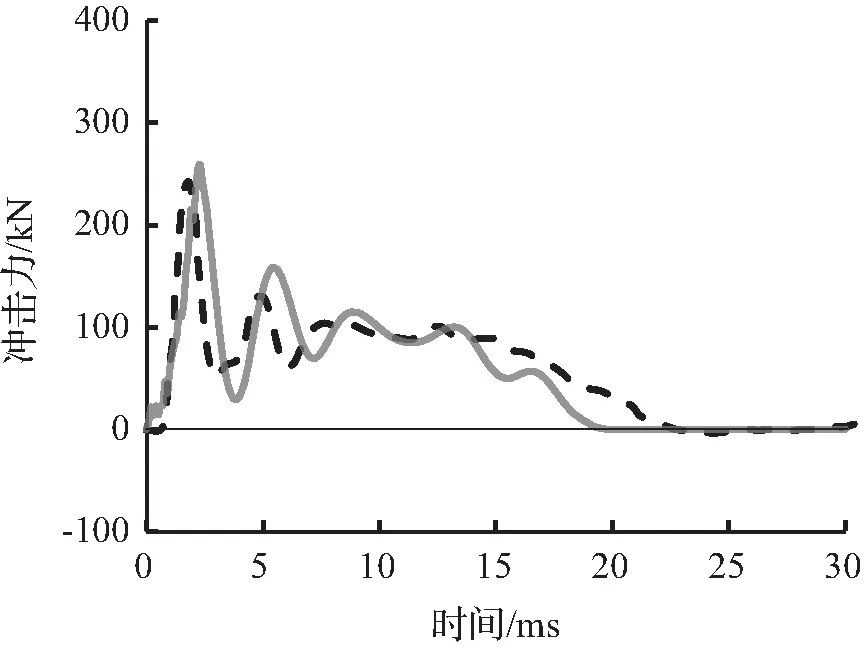
(c) 0.60 m
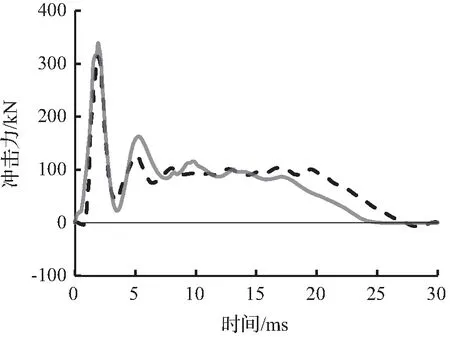
(d) 1.20 m

图6 S1616冲击力时程曲线对比Fig.6 Comparison of impact force time history curves for S1616
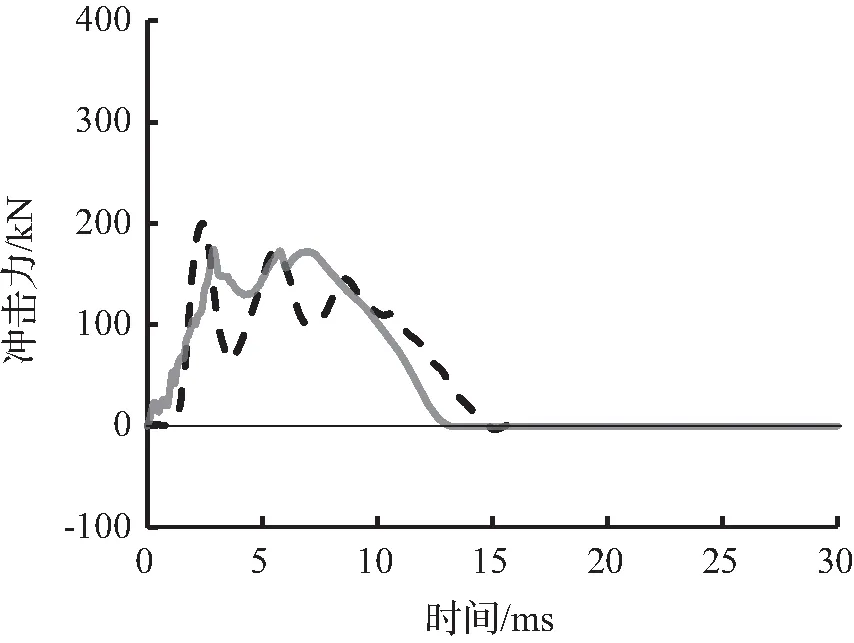
(a) 0.30 m
(b) 0.60 m
(c) 1.20 m

(d) 2.40 m

图7 S2222冲击力时程曲线对比Fig.7 Comparison of impact force time history curves for S2222
2.2 跨中位移时程曲线对比
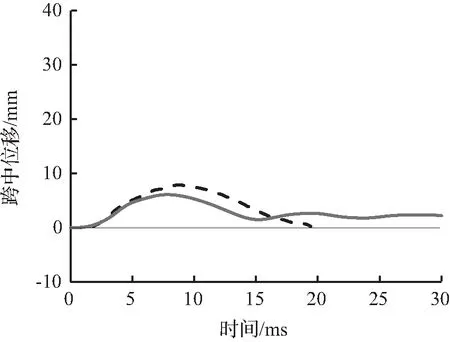
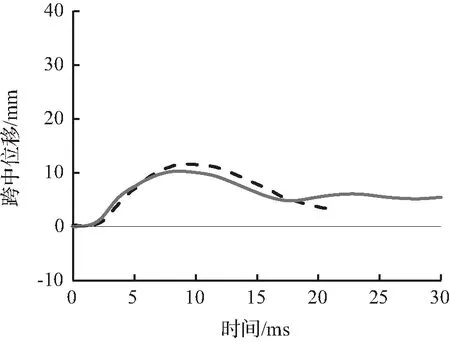
图8至图10为试件的有限元模拟所预测的跨中竖向位移时程曲线与试验跨中竖向位移时程曲线对比。从图8至图10中可以看出,有限元模拟所预测的跨中竖向位移时程曲线略低于试验跨中竖向位移时程曲线,这主要是因为试验所采用的材料有一定的初始缺陷或损伤,整体结构刚度略低,而有限元模型并没有考虑结构的初始缺陷。
(a) 0.30 m
(b) 0.60 m
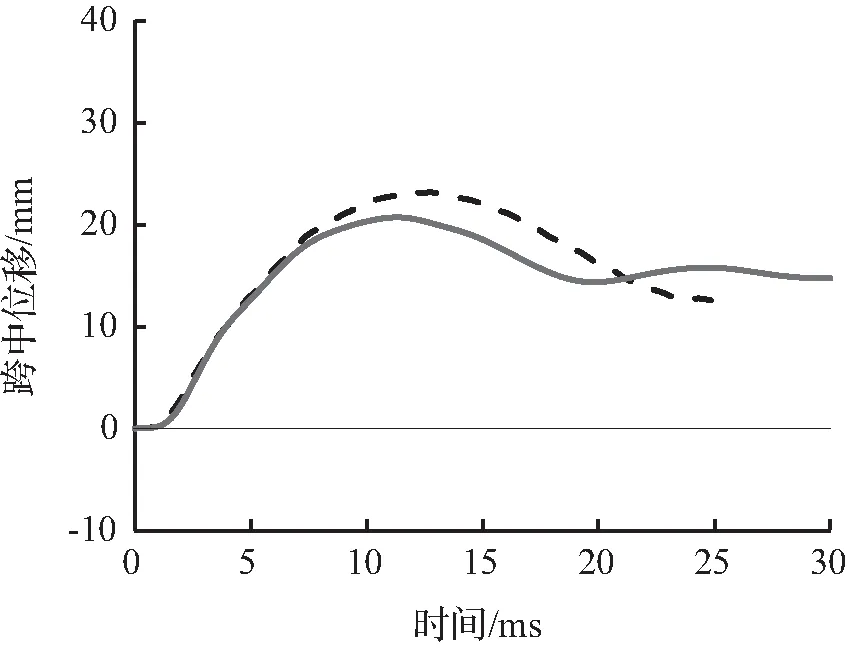
(c) 1.20 m
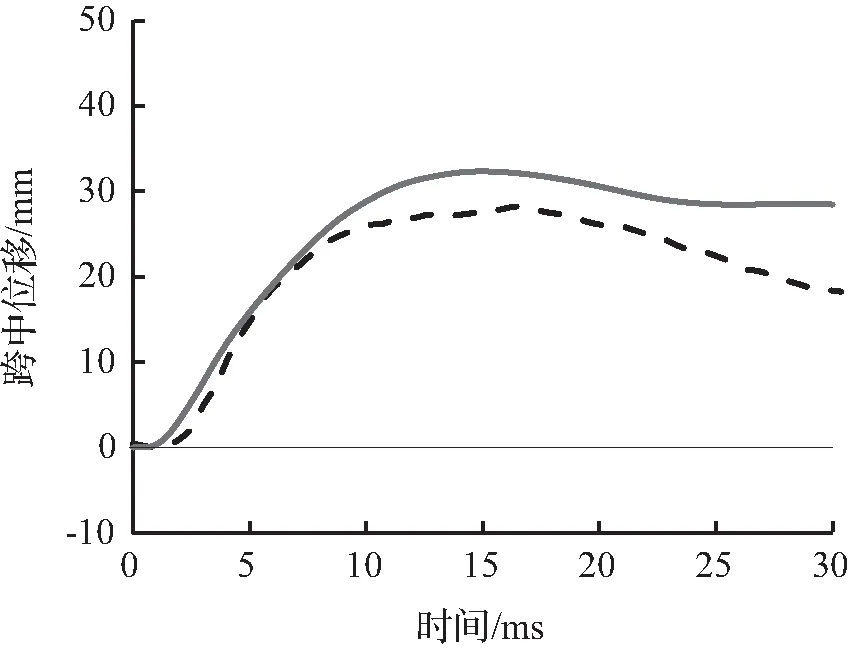
(d) 2.40 m

图8 S1322跨中位移时程曲线对比Fig.8 Comparison of mid-span displacement time history curves for S1322
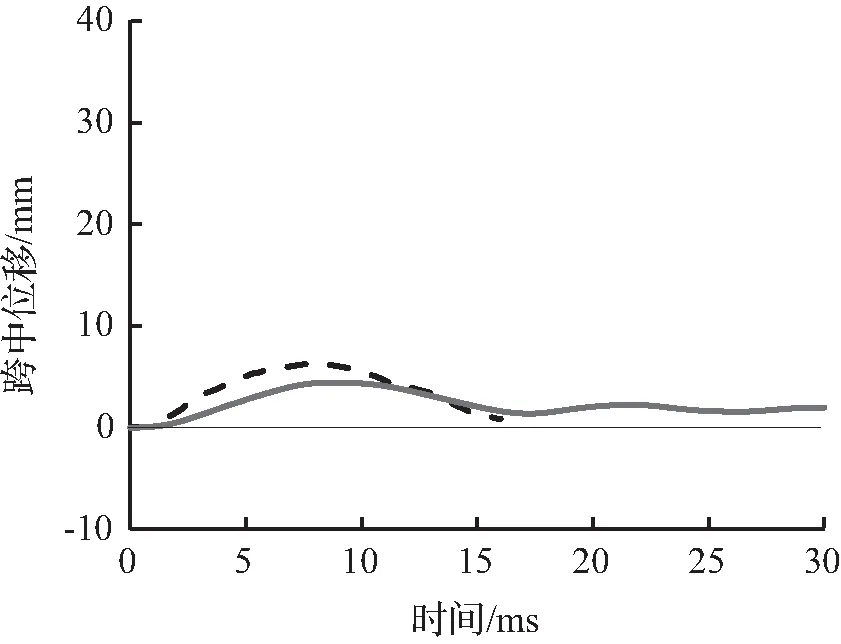
(a) 0.15 m

(b) 0.30 m
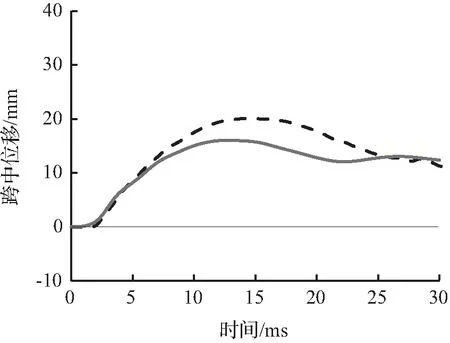
(c) 0.60 m
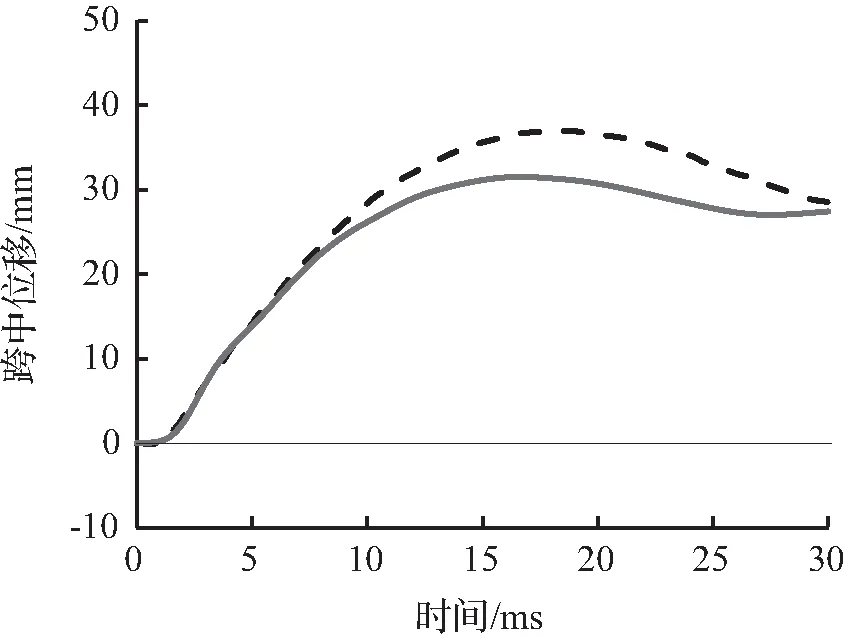
(d) 1.20 m

图9 S1616跨中位移时程曲线对比Fig.9 Comparison of mid-span displacement time history curves for S1616
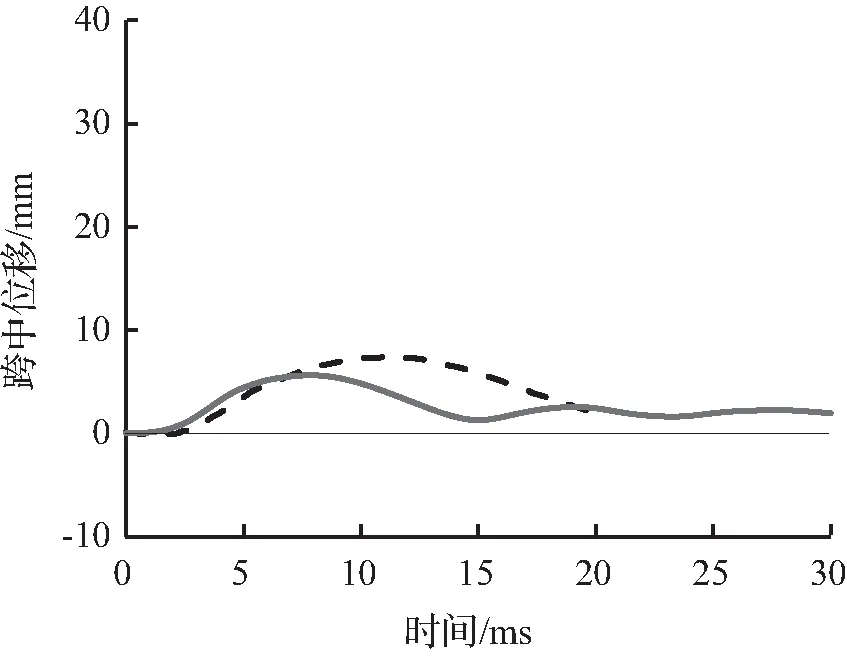
(a) 0.30 m

(b) 0.60 m
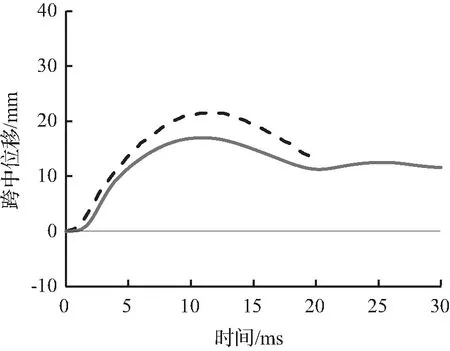
(c) 1.20 m
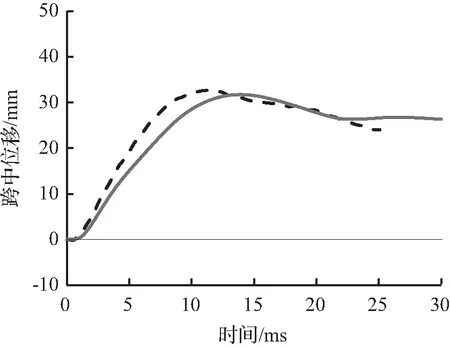
(d) 2.40 m

图10 S2222跨中位移时程曲线对比Fig.10 Comparison of mid-span displacement time history curves for S2222
2.3 破坏模态对比
图11至图13为试件有限元模型和试验的破坏模态对比。通过对比可以发现,试件破坏都是发生在冲击点附近,跨中梁底破坏严重。有限元模型破坏模态与试验几乎一致,由此可以说明有限元模型可以较好的预测出RC梁在冲击荷载作用下的破坏模态。

图11 S1322破坏模态对比Fig.11 Comparison of failure modes between test and simulation of S1322
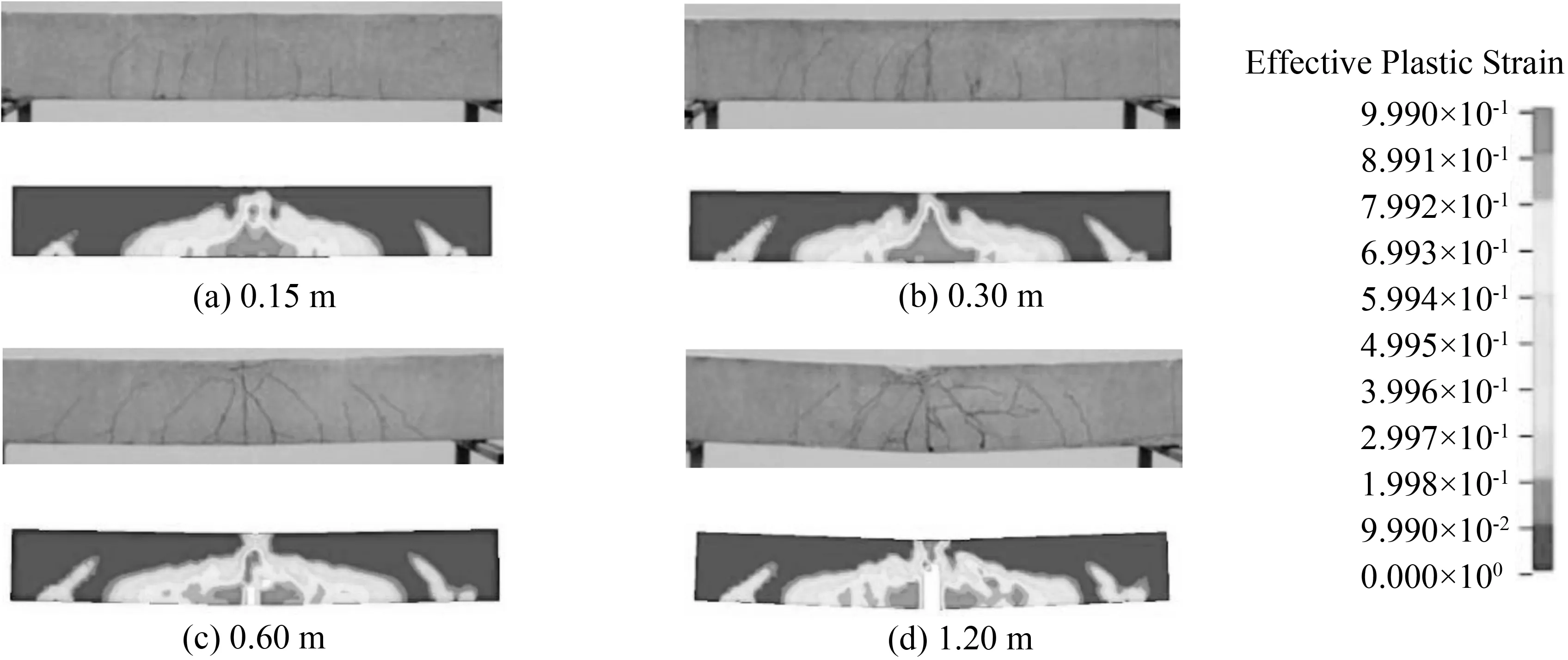
图12 S1616破坏模态对比Fig.12 Comparison of failure modes between test and simulation of S1616

图13 S2222破坏模态对比Fig.13 Comparison of failure modes between test and simulation of S2222
3 拓展参数分析
利用校核后的数值模型研究配置不同曲率半径锤头的落锤对RC梁抗冲击性能的影响。本文模拟采用的钢筋混凝土梁的几何尺寸、配筋形式和边界条件与文献[9]中试件S2222相同。
3.1 锤头曲率的影响

R90

R200

R400

FLAT

图15 不同锤头冲击力时程曲线对比Fig.15 Impact force time history curves fordifferent head geometries
如图14所示,本研究考虑了半径为90 mm的半球面(曲率为0.011 1)、曲率半径为200 mm的曲面(曲率为0.005 0)、曲率半径为400 mm的曲面(曲率为0.002 5)和曲率半径无穷大的平面(曲率为0),共4种锤头,分别命名为R90、R200、R400和FLAT。由于不同曲率半径的锤头会导致锤头的体积不同,为了便于比较,通过改变锤头的材料密度,使落锤的质量保持在400 kg。落锤以4.85 m/s的速度冲击RC梁跨中。
从模型中提取RC梁在不同曲率半径的落锤冲击下的冲击力时程曲线,如图15所示。需要说明的是,由于落锤与钢筋混凝土梁之间复杂的相互作用,在每个试件中均出现第二个冲击力峰值。由于第一个冲击力的峰值远大于第二个冲击力的峰值,所以第一个冲击力决定了梁的性能。因此,本研究仅对第一次冲击作用下钢筋混凝土梁的动力响应。
从图15中可以看出随着锤头曲率半径的增大,冲击力时程曲线加载段的斜率越大,加载速率越快。表2为不同曲率半径锤头对应的冲击力峰值及峰值到达时间。从表2数据可以看出,配置曲率半径为90 mm锤头的落锤所对应的冲击力峰值最小,为358.88 kN。随着曲率半径的增大,冲击力峰值也在提高,当锤头曲率半径达到无穷大时,其所对应的冲击力峰值达到最大,为1 344.04 kN,是曲率半径为90 mm时的3.75倍。且随着锤头曲率半径的增加,峰值到达时间由2.00 ms提前到0.30 ms。即锤头曲率半径越大,冲击力峰值越大,冲击力峰值到达越早。

表2 冲击力峰值及峰值到达时间Tab.2 Table of peak impact force and peak arrival time
根据之前的研究[16],接触面积会影响接触刚度,从而影响冲击力。对于有一定曲率的锤头,接触面积随着冲击点局部压痕深度的增加而逐渐增加到最大,冲击力峰值发生在接触面积最大时。当锤头曲率为0时,锤头以其全部底面直接接触RC梁,接触面积在极短时间内达到最大值,冲击力同时达到最大。锤头曲率半径的提高使得落锤与RC梁接触面积变化,进而引发接触刚度的提高,增大冲击加载速度,同时提高冲击力峰值。
图16对比了30 ms时的R90和FLAT平头落锤对RC梁的破坏模式。图16中可知R90组在冲击区局部损伤比FLAT组严重,部分混凝土构件受到损伤。结果表明,随着锤头曲率半径的提高,冲击力峰值随冲击速度增加的增速更快。有一定曲率的锤头对RC梁冲击区损伤更为严重;曲率为0的锤头对RC梁负弯矩区损伤较为严重。

图16 不同锤头破坏模态对比Fig.16 Effective plastic strain contours of RC beams by drop weight with hemispherical and flat head
3.2 落锤冲击角度的影响
在冲击试验中,落锤一定高度垂直落至RC梁顶面。为了控制落锤的运动,采用导轨来保证落锤在指定的冲击位置接触RC梁,防止其撞击后坠落到地面。然而,落锤与导轨之间的初始间隙和摩擦会使得落锤产生初始倾角,如图17所示。为了研究配置不同头部曲率半径锤头的落锤在不同倾斜角情况下对冲击力的影响,对不同初始倾斜角(0°、0.5°、1°和2°)的情况进行分析。需要说明的是,倾角是本研究中横梁顶面法向量与落锤中心轴之间的夹角。且设置落锤重量为400 kg,在不同初始倾斜角下以4.85 m/s的速度撞击RC梁。
配置不同曲率半径的落锤对应的冲击力峰值如图18所示。从图18中可以看出,随着倾角从0°增加到2°,当锤头曲率半径达到无穷大时,对应的冲击力峰值从1 344.04kN显著减小到751.37kN,冲击力峰值减小了44.10%。这是因为初始倾斜角减小了落锤与横梁的有效接触面积,即只有部分头部表面与横梁接触。相比之下,最初的倾斜角度对带有一定曲率半径锤头的冲击力峰值的影响微不足道,因为落锤的轻微的初始倾角对其接触面积的影响较小。

图17 冲击角度示意图Fig.17 Schematic diagram of impact inclination angle

图18 不同冲击角度下冲击力峰值Fig.18 Comparisons of the maximum impact force for impact inclination angle
综上所述,在不同的落锤初始倾斜角下,配置有一定曲率锤头的落锤所测得的冲击力峰值更加稳定。在冲击试验中使用的落锤配置有曲率为0的锤头时,应考虑落锤的初始倾斜角。采用有一定曲率的锤头可以有效降低落锤初始倾斜度对冲击载荷的影响。
3.3 落锤冲击速度的影响
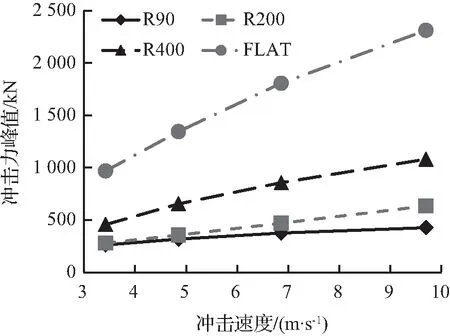
图19 不同速度下冲击力峰值Fig.19 Peak impact force with impact velocities
随着冲击速度的增加,落锤的曲率半径大小对冲击力峰值的影响越来越明显。当重量为400 kg的落锤按冲击速度分别为3.42、4.85、6.86、9.70 m/s冲击RC梁时,从图19中可以看出,冲击速度为3.42~9.70 m/s,无论落锤锤头的曲率半径如何,最大冲击力几乎随冲击速度的增加而线性增加。随着锤头曲率半径的提高,冲击力峰值增长斜率也随之增大。随着冲击速度从3.42 m/s增加到9.70 m/s,FLAT组和R90组的最大冲击力分别增加了138.8%和63.1%。这是因为冲击力取决于冲击能量和接触刚度。在相同的速度下,由于质量相同,则FLAT组和R90组落锤的冲击能量是相同的。而锤头不同的曲率半径使接触面积发生改变,导致了接触刚度的变化,进而对冲击力峰值产生影响。
4 结论
基于ANSYS/LS-DYNA建立有限元模型,通过对比试验结果以验证模型的准确性。之后通过对有限元模型开展拓展参数分析,得出如下结论:
① 采用ANSYS/LS-DYNA所建立的精细化有限元模型可以很好地模拟混凝土梁受冲击荷载作用的破坏模态、冲击力时程曲线以及跨中竖向位移时程曲线。
② 冲击力峰值随落锤头表面曲率半径的增大而增大,而冲击力峰值到达时间随落锤头表面曲率半径的增大而提前。有一定曲率的锤头对RC梁冲击区混凝土损伤更为严重;曲率为零的锤头对RC梁负弯矩区混凝土损伤较为严重。
③ 不同的落锤初始倾斜角下,配置有曲率大于零的锤头所测得的冲击力峰值更加稳定。采用曲率大于零的锤头可以降低落锤初始倾角对冲击力的影响。
④ 随着锤头曲率半径的提高,冲击力峰值随冲击速度增加的增速更快。
