中算史内容的现代发掘与应用举隅

2021-09-01罗见今

内蒙古师范大学学报(自然科学汉文版) 2021年5期

罗见今

（内蒙古师范大学科学技术史研究院，内蒙古呼和浩特010022）

因数学发展的需要，数学史家、数学家和数学教师对中算史的认识和应用各有侧重，将历史的研究同现代发展联系起来不乏成功的先例：吴文俊先生发掘宋元数学、揭示数学机械化的内涵，应用于机器证明，是古为今用的典范，彰显出数学史研究的目的。本文举出中算史8个例子，说明后人从区组设计和组合计数如何认识、应用和发展这些传统题材。

1 洛书与拉丁方：组合设计应用正交拉丁方构造幻方

20世纪60年代以来兴起的组合数学（combinatorial mathematics，combinatorics），是伴随计算机科学而发展的现代数学分支，当年有影响的《组合数学》（1962）在介绍书名时写道：“这是一门起源于古代的数学学科。据传说中国皇帝禹（约公元前2200年）在一个神龟的背上观察到纵横图。”［1］图1所示的数字方阵为“洛书”，即三阶幻方。洛书成为现代组合数学起源的标志，在国际上得到公认。

图1 洛书Fig.1 Luoshu

幻方的一种实数类比称为双随机矩阵，应用它可以找出达到最佳经济效益的多因素配置方案。现代对幻方的研究，有奇数幻方、素数幻方、级数幻方、双重幻方（不仅行、列、对角线的和一定，而且它们的积也一定）［2］、复数幻方、优美幻方等等，还向三维发展，讨论幻体的构造［3］。国际上对幻方功能、富兰克林幻方等都有研究。

欧洲中世纪将扑克牌中A、K、Q、J四种16张牌排列成方形，使得每横行、每纵列均包含这四种牌，这种方阵即拉丁方。其实这种排法至迟战国时就出现在玄戈占星表上［4］（图2）。

图2 玄戈占星表构成一个四阶拉丁方Fig.2 Xuange astrology table forms a fourth order Latin square

在组合数学的基本内容区组设计（block design，BD）中，正交拉丁方成为西方的兴趣点之一，例如1960年构造出高阶正交拉丁方，欧拉关于三十六军官问题的猜想不成立①，轰动一时。而幻方研究一般却归于代数学［5－6］。

幻方构造在中国既是一个古老的神秘课题，又是一个现代的研究对象［7－8］，有较多论著［9］。但一般未从组合数学BD的角度提出和解决问题。其实幻方与拉丁方有密切联系。新近的研究表明，可通过构造两正交6m+3阶拉丁方，将其组合而获得6m+3阶全对称幻方，说明幻方与正交拉丁方存在内在联系，幻方能够成为BD研究的一个新领域。

2 莱布尼兹怎样看卦序与方位：伏羲六十四卦的对称结构

邵雍六十四卦方位图（图3）中，方图的排序在诸本易卦中独树一帜，各卦彰显出数字性质。孙小礼［10］等学者的论文提到莱布尼兹（G.W.Leibniz，1646—1716）在《二进算术》（1679）中建立了二进制的表示及运算，1703年他给法国科学院提交“关于仅用0与1两个符号的二进制算术的说明，并附其应用以及据此解释古代中国伏羲图的探讨”。莱布尼兹将阴爻和阳爻与0和1对等，是发现这种对等关系的第一人。如果应用数学方法分析易卦的卦序，以此为切入点，用二进制的视角去研究易卦的性质，这正是莱布尼兹方法的要点。要透彻认识易经，二进制数学是一有力的工具。

图3 伏羲六十四卦方位图Fig.3 Fu Xi’s sixty-four hexagrams position map

现将邵雍所绘伏羲六十四卦方位图（图3）中的方图按逆时针方向旋转135°，得到一个菱形图（图4）：63乾在上，0坤在下，左07为否，右56为泰。垂直的乾坤轴与水平的否泰轴相交于菱图的中心。然后按莱布尼兹二进制，算出各卦位的卦值。如：

图4 邵雍先天图的中心方图Fig.4 The central square of Shao Yong’s congenital chart

今本周易的卦位、卦名、卦值依序为：1乾63，2坤0，3屯34，4蒙17，…，64未济21。菱图中在63的位置填入1，在0的位置填入2，…，在21的位置填入64。然后将1—2，3—4，…，63—64连接起来，得到周易卦序的结构图（图5），本文称其为邵雍先天二进卦值菱图（简称菱图）。

菱图具有三种基本置换和对应，每种都决定了一个二元组（或有序对）。分析会发现图5的映射和对应关系，例如随38↔25蛊随38↔52归妹随38↔11渐离45↔18坎益35↔28恒；等等。这说明乾坤轴与否泰轴的对等性。用二进卦值表示的邵雍先天菱图具有许多明显的数学性质，用细线将上述三种对应连接起来，就构成直观的、对称的几何图像；对纵、横、斜线两端的数字分别做四则运算，能得到许多相仿而有趣的结果，此不详论。于是，今本周易卦序结构的真相完整地展现在世人面前［11］。周易的卦序呈现出优美的对称性和完备的均衡性，全部有序对勾画出卦序的结构，展示了深奥的易理意境和高超的构造方法。因此可以提出“易经卦序结构”的概念。卦序可以转换为形象的对称结构意味着什么？这给易理研究提出一个新课题。

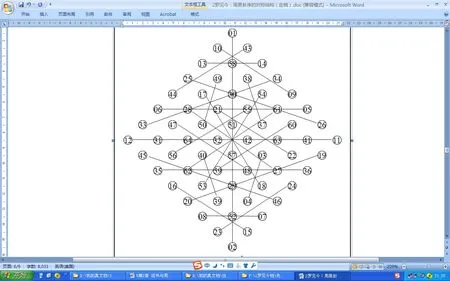
图5 周易卦序的对称结构图Fig.5 Symmetrical structure diagram of hexagram order in the Change Book

3 徐利治和高尔德如何将朱世杰-范德蒙公式拓展为现代研究

1923年钱宝琮“朱世杰垛积术广义”［12］将《四元玉鉴》中一个垛积恒等式推广，表述成现代形式——卷积型组合恒等式，后来形成了现代计数组合论中使用的术语“the Chu-Vandermonde formula”，即“朱世杰-范德蒙公式”，它是组合计数论的一个基本公式。

朱世杰《四元玉鉴》“茭草形段”第4题给出的关系利用组合与求和符号可表示为

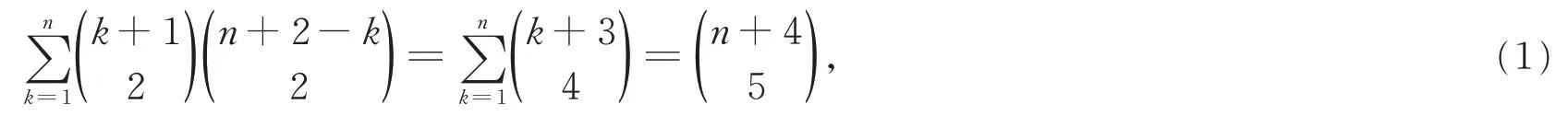
而《四元玉鉴》“果垛叠藏”第6题可表示为

将上两式推广，获得

现代科学史学科的奠基人、科学史家乔治·萨顿（G.Sarton）在他的名著《科学史导论》［13］中将钱先生总结的这一公式介绍到西方，1955年李约瑟的《中国的科学与文明》［14］第3卷数学中也引用了这一结果，西方数学家通过这一传播渠道了解到朱世杰的工作。

算法和程序设计技术的先驱者、美国斯坦福大学教授克努特（Donald E.Knuth，中文名高德纳）在其荣获图灵奖的名著《计算机程序设计艺术》［15］中，第59页讲“the Chu-Vandermonde formula”，指明朱世杰的组合公式在先，在第70页还留了一道题目，要求证明“朱-范公式”。在国际组合数学界，“朱-范公式”已成为一个基本公式。

徐利治介绍朱-范公式的现代发展［16］，其中有他和美国高尔德（H.W.Gould）的成果。二百多年来，朱-范公式已有Rothe（1793），Gauss，Hagen（1891），Gould（1956），Handa和Mohanty（1969）等人的多种扩充，应用甚广。从历史上看，德国数学家高斯（Karl Friedrich Gauss，1777—1855）研究超比例级数时曾将类似的卷积关系推广到复数的情形［17］，被称为“Gauss-Vandermonde”公式。Rothe-Hagen-Gould的卷积型恒等式可写成［18－19］

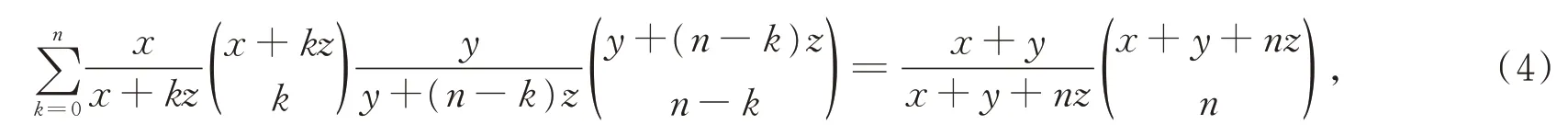
其中，Hagen的恒等式为［20］

有多种卷积公式均可由朱-范公式推广而获得，此不一一列举和证明。注意到组合数学界感兴趣的事实——历来公认为Rothe-Hagen-Gould卷积型恒等式是朱-范公式的“非平凡推广”（non-trivial extension），这里有必要说明，只需利用Hsu-Gould inversion［21］（徐利治-高尔德反演）公式，即可证明（4）式可由朱-范公式推证。说明（4）式实质上仍与原始的朱-范公式等价，详见文献［18，21］。

4 Chinese Game of Nim：博弈论、图论一个深奥的游戏模型

在古代数学书中数学游戏虽不见记载，但一些特殊的游戏确实包含了深奥的数学内容。我国民间流传一种二人数学游戏，其规则如下：有k堆物件，每堆物件数量不同，两人轮流从中拿取，每次只能在其中一堆中至少取一个，至多取一堆，最后谁取完谁胜（或负）。k=3时北方叫作“抓三堆”；南方叫“拧法”或“翻摊”；国外称为Chinese game of Nim［22］、simple game of Nim或Fan Tan［23］，表明这种游戏源于中国。Nim游戏从古代流传至今，闪耀着先人智慧之光，现已遍及世界，引起了数学界的兴趣和重视。

Nim作为数学游戏的名称，在西方不迟于15世纪。美国人弗兰克尔（A.S.Frankel）认为Nim是世界上最古老的游戏，它起源于几千年前的东方［24］。穆尔（E.H.Moore）提出了一种p阶Nim，成为图论Nim型对策第三定理的主要例子［23］。

可利用求布尔和来寻找Nim的制胜方法如下：将三堆的数目例如11，22，29，用二进制表示出来（图6），规定一种特殊的加法，即1加1为0，1加0为l，0加0仍为0。叫“点加”或“模2加”，加出来的和叫作“点和”或“布尔和”，这种加法在研究群、环、域的近世代数或逻辑代数中很有用。

图6 二进制数字的加法Fig.6 Addition of binary numbers

如果规定谁取最后1个谁输，那么甲方取出的数字一定要保证所余三堆数字的布尔和为0，轮到乙方来取时，无论他取出多少，只要甲方步步不错（即布尔和总保持为0），等待乙方的必然是取最后1个，失败。

百年来随着数论、近世代数、逻辑代数、特别是对策论、图论和组合数学的发展，当用新的眼光观察Nim时，它作为一种数学模型，又给人以新的启示。于是Nim升格为一个新的数学名词，开始在数学论文和专著中出现。

在图论中Nim受到重视。法国贝尔热（C.Berge）在《图论及其应用》（The Theory of Graphs and its Applications，1962）中开辟第六章介绍“在一个图上的对策”，主要就是定义“Nim型对策”，这里的对策，即游戏或博弈（game）。这个图不能有由首尾相接的有向边所组成的圈，不然游戏就有可能无限进行下去。经过严格定义的Nim型对策，揭示了Nim的特性，扩展了Nim的外延，使得一些图的游戏、扑克游戏、数字游戏等都归于这一类。“抓三堆”Nim就成为一特例。从Nim型对策还可引出四个定理，能够保证制胜的结局，此不赘言。

Nim制胜方案如表1，可视为Nim三元系。拓展的研究表明［25］：与斯坦纳三元系相同。限于篇幅，这里不再对斯坦纳（J.Steiner，1796—1863）三元系进行说明。Nim制胜方案变成了一个区组设计的结果。特别有趣的是，它恰为科克曼（T.P.Kirkman，1806—1895）在1851年所给出的著名的“十五个女学生问题”的排列方案（只是区组顺序有别）。这当然不仅仅是巧合，中国古代Nim包含有深奥的数学道理，在组合数学中具有基本的重要性，其规则的简明性与内涵的深刻性互为表里，自相辉映。

表1 “抓三堆”Nim制胜方案Tab.1 Nim winning plan

5 明代王文素《算学宝鉴》“三同六变”题与科克曼“女生问题”

王文素（1465？—？），字尚彬，山西汾州（今汾阳市）人，明代数学家，1524年完成巨著《新集通证古今算学宝鉴》12本42卷，近50万字，所惜当时未能出版。民国年间由北京图书馆于旧书肆中发现一蓝格抄本，收购入藏。1993年，王文素《算学宝鉴》抄本影印版由《中国科学技术典籍通汇·数学卷》［26］刊出。2008年，《算学宝鉴校注》［27］由科学出版社出版，标志着对王文素的研究进入一个新阶段。

《算学宝鉴》中有一问题“三同六变”（图7）：“假令二十四老人，长者寿高一百，次者递减一岁，止于七十七。共积总寿二千一百二十有四。卜①卜，占卜。用占卜的方法确定聚会的地址。会三社，八老相令（会）七百八岁，盖因人情逸顺，散而复令（会），更换六次，其积仍均七百有八，此见连用之道。”

该题意即：有m=2nk=24位老人聚会，年龄从100岁到77岁，依次相差1岁，共2 124岁。2k=8人分到一“社”（组，S），共有n=3组，每组年龄和皆p=708岁；3组为一变局（T）。问能编成多少不同组（S）？能构成多少相异局（T）？

他给出的6种答案绘在图7中，最后他说道：“其变尤多，不及备载”，明确指出求变局之数很难，这就提出了“王文素问题”，须找出共有多少种方案。

图7 王文素《算学宝鉴》“三同六变”图文Fig.7 The diagram and text of“Three sames and six changes”in Wang Wensu’s Suan Xue Bao Jian

这是一种复杂约束条件下的组合问题，李培业［28］②“李珍”是李培业署名。较早认识到它的组合性质。笔者认为，“王文素问题”可分为三类子问题：连续数组、偶数组和奇数组问题（不详论），运用组合方法，可以得到［29］：

组（1）：｛78，80，82，88，90，94，96，100｝；组（10）：｛78，82，84，86，90，92，96，100｝；

组（2）：｛78，80，84，88，90，92，96，100｝；组（11）：｛78，80，84，86，90，94，96，100｝；

组（3）：｛78，82，84，88，90，92，94，100｝；组（12）：｛78，80，82，86，92，94，96，100｝；

组（4）：｛78，80，82，84，92，94，98，100｝；组（13）：｛80，82，84，88，90，92，94，98｝；

组（5）：｛78，80，82，86，90，94，98，100｝；组（14）：｛78，82，84，88，90，92，96，98｝；

组（6）：｛78，80，84，86，90，92，98，100｝；组（15）：｛78，80，84，88，90，94，96，98｝；

组（7）：｛78，80，86，88，90，92，96，98｝；组（16）：｛80，82，84，86，90，92，96，98｝；

组（8）：｛78，82，86，88，90，92，94，98｝；组（17）：｛78，82，84，86，90，94，96，98｝；

组（9）：｛80，82，86，88，90，92，94，96｝；组（18）：｛78，80，84，86，92，94，96，98｝。当然这不是全部，还可以找到许多连续数组和奇数组。

王文素问题产生于500年前，把一个派生能力很强的数学问题大众化，使之普及，可推衍出形形色色的问题，极具生活情趣，可以使用集合论、计数组合学和设计的方法来解决。

数学史上不乏一些著名组合问题，如约瑟问题、科克曼女生问题、夫妇入座问题等，女生问题也并非一开始就变成了世界著名难题［30］，而是在百余年的认识过程中逐步形成，它与王文素问题形式相似，条件不同，解法相异。王文素问题涉及连续自然数在不同约束条件下适当配置，聚为一些等值数组，构成若干相异数局，属于在组合计数基础上的区组设计。

6 明安图-卡塔兰数：高德纳的评说和拉坎布的证明

卡塔兰（E.C.Catalan，1814—1894）1838年提出了Cn，后来被称为卡塔兰数（Catalan numbers）［31］，Cn的定义式为

n≤10的数列如下：1，1，2，5，14，42，132，429，1430，4862，…。

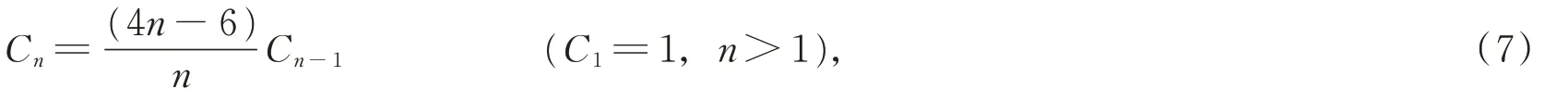
1758—1759年间，数学家欧拉（L.Euler）公布了对n＜23的正确的Cn值［32］，还给出了表示Cn+2的公式。毕纳特（J.Binet）1839年获得了Cn的生成函数［33］，卡塔兰数有两个递推公式，在基础论著《组合学导引》［34］中有详细介绍，即

卡塔兰序列至少有50种组合解释，应用广泛，已成为与斐波那契数（Fibonacci numbers）、斯特灵数（Stirling numbers）类似的一个基本计数函数。在世界数学史上，第一个提出卡塔兰数并有大量研究和应用的，却是清代蒙古族科学家、钦天监监正（国家天文台台长）明安图（1692？—1763？）。他在《割圜密率捷法》（1839）第三卷（原稿1730年代撰成）中给出

这是一个数学界未知的公式。在计算中明安图应用了式（3），他并得到：（|α|＜π/2），

笔者1988年在《内蒙古大学学报》上发表《明安图是卡塔兰数的首创者》［35］。算法和程序设计技术的先驱者、斯坦福大学Donald E.Knuth（克努特，中文名高德纳）教授在获图灵奖的名著《计算机程序设计艺术》中，论述了图论中trees树的概念，专辟一节回顾卡塔兰数的历史。其中“中国蒙古族数学家明安图1750年前在研究无穷级数时算出了卡塔兰数，但他没有将其同树或别的组合对象联系起来”［36］，引用了笔者1988年的论文。

英国德尔比大学的拉坎布（P.J.Larcombe）博士在此基础上，2001年发表《论卡塔兰序列生成函数：一个历史的透视》［37］，指出明安图的方法是一种生成函数法，并证明了该法的正确性。拉坎布研究明安图所创卡塔兰数共发表了12篇相关论文。

明安图的成果与卡塔兰数西方早期研究相比，具有独辟蹊径的特点，即令对今天的学者来说，也是十分新奇的。由于明安图是卡塔兰数的首创者，早于卡塔兰约100年，李文林教授主张，Cn应当称为“明安图-卡塔兰数”。

7 戴煦的正切数与欧拉数：区别于西方传统的递推公式

正切数T（ntangent number）和欧拉数E（nEuler number）是两种重要计数函数，也是特殊函数和递归函数。西方对正切数的研究1857年开始，远不及对欧拉数的认识［38］。

戴煦（1805—1860），字鄂士，浙江钱塘（今杭州市）人，晚清著名数学家。1852年在《外切密率》［39］第四卷中使用具有特色的递归方法，同时获得现今所说的正切数和欧拉数的递推公式（略），成绩斐然。他算出前十个正切数（图8）：

图8 戴煦求得的正切数表Fig.8 Table of tangent numbers obtainedby Dai Xu

T1=1（原著未列）；T2=2（第一乘法）；

T3=16（第二乘法）；T4=272（第三乘法）；

T5=7936（第四乘法）；T6=353792（第五乘法）；

T7=22368256（第六乘法）；T8=1903757312（第七乘法）；

T9=209865342976（第八乘法）；T10=29088885112832（第九乘法）。

他已完全掌握了正切数T n的递推规律，得到

戴煦同样正确地算出了前十个欧拉数（图略）：

E0=1（原著未列）；E1=1（第0乘法）；

E2=5（第一乘法）；E3=61（第二乘法）；

E4=1385（第三乘法）；E5=50521（第四乘法）；

E6=2702765（第五乘法）；E7=199360981（第六乘法）；

E8=19391512145（第七乘法）；E9=2404879675441（第八乘法）。

可知他已完全掌握了欧拉数E n的递推规律，从而获得正割幂级数展开式

经比较，戴煦把T n和E n相提并论，定义酷似，且相补充。他的基本思想是两者相匹配、相“对称”。因而在他的原著中，全部论述和结果都保持这种“对称性”，这与现代数学中将欧拉数同伯努利数（Bernoullinumbers）相提并论的做法是不一样的。

20世纪西方对正切数的文献有：Estanave［40］（1902）研究tgx、secx展开式系数；Schwartz［41］（1931）应用麦克劳林公式展开tgpx；Toscano［42］（1936）给出了有关交错置换和正切数的另一种表述；Entrenger［43］（1966）和Knuth，Buckholtz［44］（1967）用组合数学计数的观点，通过欧拉数与伯努利数来研究正切数，后者给出正切数前60个数值。

8 李善兰、夏鸾翔、华蘅芳的幂和公式与现代发展

幂和问题具有悠久的历史［45］，晚清算家亦有不凡贡献。限于篇幅，这里只提出部分结果。

李善兰（1811—1882）独创欧拉数（表2），见于《垛积比类》（1845？）第7表，李氏还给出它的递归定义（略）。

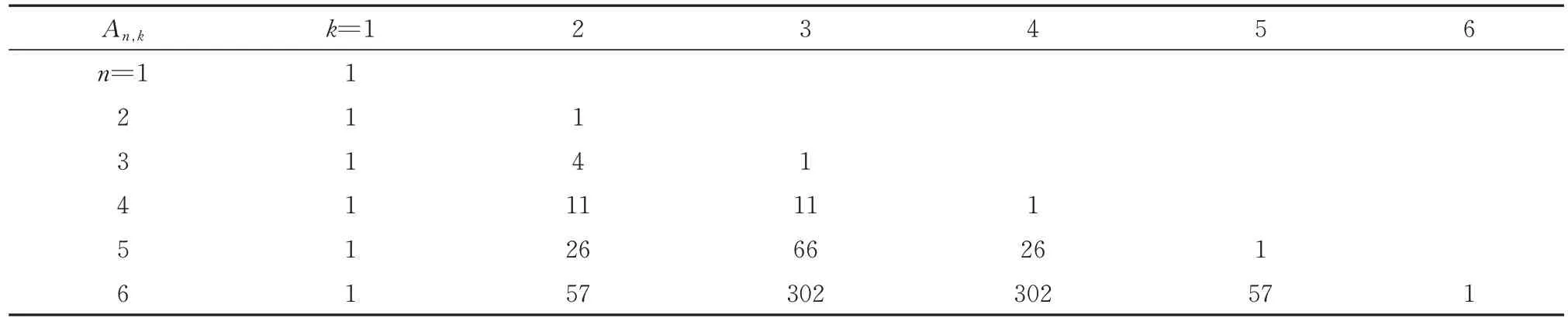
表2 欧拉数A n，k（比较《垛积比类》第7表）Tab.2 Eulerian numbers A n，k

《垛积比类》“乘方垛解义”获得式（13），据“乘方垛求积术”求自然数前m项n次幂和式（14）为

即李善兰将幂和分解成n类组合之和，每类组合的个数依欧拉数分布。这个幂和公式简洁优美，可求任意次幂和。

夏鸾翔（1823—1864）在《洞方术图解》“单一起根诸乘方诸较图”中创“夏氏数”（表3），表出乘方公式（15），继而获得自然数前m项的幂和公式（16）为

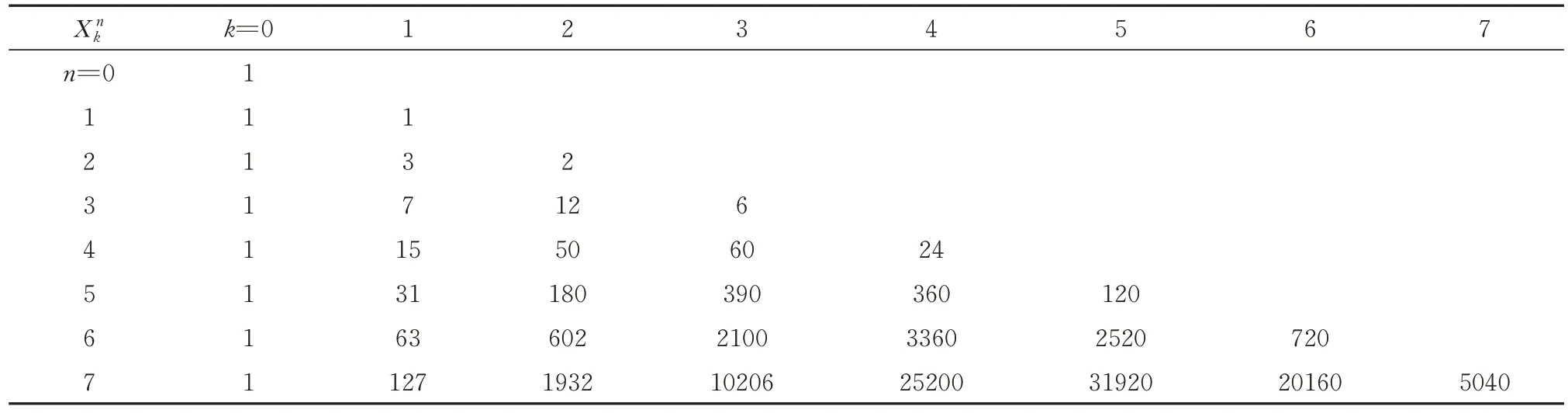
表3 夏氏数（据单一起根诸乘方诸较图）Tab.3 Xia Luanxiang’s numbers

X nk=01234567 k n=0 1 1 1 1 2 1 3 2 3 1 7 126 4 1 15506024 5 1 31180390360120 6 1 63602210033602520720 7 1 1271932102062520031920201605040

即将幂和分解成n+1类组合之和，每类组合的个数依夏氏数分布。运用计数函数求幂和的公式中，如以计算量衡量，该式最简，迄今仍是佼佼者。

华蘅芳（1833—1902）《积较术》“诸乘方正元积较表”用现今所说的有限差分法提出一种计数函数“华氏数”（表4），给出它的递推定义式，将它应用于求乘方以及求幂和

李善兰从垛积术（和分）、华蘅芳从招差术（差分）各自获得幂和公式，可谓殊途同归。华氏数具有优秀的性质，将它的定义稍作改变，即将表4中的数字取绝对值，针对幂和问题可以建立起“取盒—放球”模型，给它一个全新的组合解释［46］。

表4 华氏数（据诸乘方正元积较表）Tab.4 Hua Hengfang’s numbers

hnk=012345678 k n=0 1 1 0 1 2 0－12 3 0 1－66 4 0－114－3624 5 0 1－30150－240120 6 0－162－5401560－1800720 7 0 1－1261806－840016800－151205040 8 0－1254－579640824－126000191520－14112040320

幂和问题极富趣味性和挑战性，形成一个专题、一种文化。数学家和爱好者构造各种数论函数孜孜以求，公式的简明性和算法复杂性可一较高下。李善兰、夏鸾翔、华蘅芳的结果具有类似而不同的结构，形式简洁优美，对计数组合论发展的贡献深远。

Sum of power of integer这样一个具有魅惑力的问题不乏现代兴趣，吸引着一些数学家。笔者查阅，仅从1968年到1980年，J.Riordan［47］、J.L.Paul［48］、S.L.Gupta［49］、M.J.A.Sharkey［50］、H.W.Gould［51］、B.Turner等人提出或用不同方法证明了这一问题或与它相关的、用组合表达的若干公式。迄今互联网上仍有不少网页涉及，盛况空前。