基于改进PID的数控机床电气控制系统优化设计
2021-08-31黄金晶王嘉卿
黄金晶,杨 凯,王嘉卿
(上海海事大学工程训练中心,上海 201305)
0 引言
在数控机床内安装控制程序,使其能够自动化控制,该程序通过逻辑性算术符号或者控制编码,对其进行译码,以代码化的数字标准形式表示。与此同时,数控机床以数据信息为载体,结合了测量、微电子、计算机、自动化和机械等最新技术,将其输入至数控控制中心,经过计算分析,对数控装置内的信号实行控制,令机床按照零件的形状以及尺寸大小自动加工,从而实现自动化的工作方式,也能很好地解决多品种、精度及复杂零件等各种加工难题。如果在加工过程中,需要临时改变零件的形状或尺寸,只需改变数控程序,即可以实现操作,并且还能够节省时间,提升生产力[1]。
数控机床在进行加工的过程中,具有稳定的加工质量;可利用自动化的操作模式降低劳动强度;还可多坐标联动,加工复杂零件,具有便于生产化管理以及存在可靠性较高等优点。但这就需要操作人员拥有较高的工作素质和维修技术[2-4]。传统方法因为计算过程较为复杂,导致工作效率较低、操作困难,为此本文设计一种基于改进PID的数控机床电气控制系统优化方法,通过改进PID技术清除线性范围内振荡效果,利用电气负荷调节系统性能,降低系统工作过程计算,提升工作效率,增强稳定性。
1 改进PID算法分析
1.1 PID反馈控制系统稳定裕量计算
PID控制下的反馈控制系统如图1所示。
设Gc(s)代表PID控制器,由图1可得PID控制器的传递函数为
(1)
kP为数据参考输入;kI为负载干扰;s为系统的误差信号;kD为系统的输出[3]。
定义控制系统的灵敏度S(s)以及灵敏度函数T(s),可以得到具体公式为:
(2)
(3)
GP(s)为被控制的对象;L(s)为系统开环的传递函数。
由于奈奎斯特图可以给出稳定的裕量信息,所以能够利用奈奎斯特曲线以及(-1,j0)点靠近程度对系统稳定性进行表示,奈奎斯特曲线和(-1,j0)点距离越远,表示系统稳定性越高。临界点(-1,j0)与奈奎斯特曲线最近的距离的表达式为
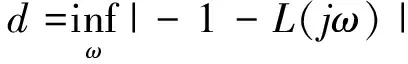
(4)

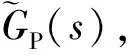
(5)

在β非常小时,令标称对象获得内部稳定的控制器Gc,从而可以稳定整体对象簇,βsup代表β上确界。如果具有一个控制器Gc能够令响应对象达到内稳定,那么βsup即为稳定裕量。
1.2 线性范围内振荡清除
通过将上述的分析作为基础,获得一种全新的PID控制器方法。将采集到的数据当成零点,并把收集到的信息和零点偏差当成误差量,通过处理输出信号,使系统获得优化。
在通常PID的调节过程中,因为系统执行线性范围会受到限制,当系统遇到非常大的扰动时,由于偏差E比较大,产生超调量,系统会产生连续大幅振荡。为了清除该现象,引入积分分离法,从而令被调量与给定值相接近时,即发挥积分的作用[6],具体表达式为
ΔU(k)=kP(e(k)-e(k-1))+kIe(k)+
kD(e(k)-2e(k-1)+e(k-2)) |e(k)|≤C
(6)
e(k)、e(k-1)、e(k-2)分别为给定值控制量、被调量1和被调量2;C为选定最大的允许偏差。
此外,为了避免由于系统频繁操作产生的振荡,要利用带死区的PID对其实行控制,具体控制公式为

(7)
U(k)为目前控制量;U为死区;K为死区的增益;B为依据系统的可调参数。此系统为非线性的控制系统,在偏差的绝对值为|e(k)|≤B时,系统的输出为K×U(k);当偏差绝对值达到|e(k)|>B时,利用改进PID方法的输出值,控制输出为U(k)。
2 数控机床电气控制系统优化设计
在设计系统过程中,电气辅助系统的控制中心采用可编程逻辑控制器,通过数字信号处理器进行伺服电机的驱动核心和机床运动控制器的操控,具体如图2所示。
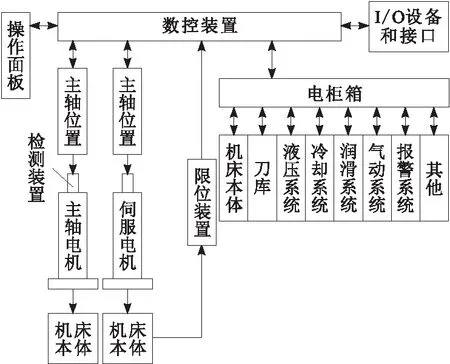
图2 数控机床的电气控制总体优化方案
本文设计的系统可以实现三维控制和运动,具体如下所述:
a.对主轴电机实现调速、停止、变速以及启动命令,同时还要求主轴能够平稳转动。
b.对冷却泵电机、液压泵等实施自动控制操作。
c.在机床运行过程中,控制信号灯。
d.保障系统的安全运行,主要设置紧急制动及工作台限位等措施。
2.1 供配电子系统优化设计
2.1.1 电源供配电子系统
380 V交流电源可对刀库电机、主轴电机、冷却泵电机以及伺服电机等实现供电操作,具体交流380 V供电电源如下所述。
将系统的供配电线路与漏电开关相结合,通过漏电开关控制整体机床的供电和停电,以此有效地避免数控机床在运行过程中,因为短路或者过载而损害机械设备的情况。通过熔断器实现热保护,在把电路分成2部分,其中,一路线路经过变压器对其进行电压改变,能够管理伺服系统,而另外一路能够对主轴、刀臂、油泵以及刀库电机等进行供电,完成供配电设计[7-8]。
2.1.2 直流电源供配电子系统
对于系统的2个控制开关,一个用来对机床工作进行控制,对所有工作系统芯片提供电压;而另外一个用来控制可编程逻辑控制器、数字信号处理器等单元模块,一些其他的电压信号不与此开关进行连接。对于此电源的开关连接端子,需要以线码的模式对其进行标记。同时,还可以为IO信号提供电源电压。
2.1.3 电气负荷子系统
在设计控制系统过程中,电气负荷选择非常重要,若选取较大,就会生成浪费,反之,如果选取较小,则可能出现供电不足,机床无法正常工作,且容易造成设备损坏等情况。因此,计算电气负荷,要十分精准、合理地进行选取[9]。
在系统设计过程中,采用多台数控机床,它们用电的功率基本一样,因此能够利用系数法对其进行计算。系数法是采用用电设备的功率,对电气负荷进行计算的方法。先全面调查系统运行情况,通过对应规则完成用电设备分组,找出所有组计算负荷关系以及设备功率,同时提供固定参数。最后利用参数区来推测系统的负荷,由于数控机床用电的功率数值基本一致,因而计算过程较为简便。具体可以得到公式为:
(8)
(9)
(10)
Pc、Qc、Sc为用电机床的有功、无功和视在功率[10];Pcj、Qcj为电机床的有功、无功电能。
2.2 刀具检测子系统优化设计
2.2.1 自动换刀
在数控机床工作时,采用自动换刀替代人工换刀,自动换刀存在2个自由度,能够减少换刀的时间成本,提升其工作效率。采用电磁阀开关控制自动换刀,使机械臂伸展和刀具夹紧,具体换刀的过程如图3所示。通过观察图3能够看出,采用机械臂的4个动作,即可实现自动换刀的工作[11]。
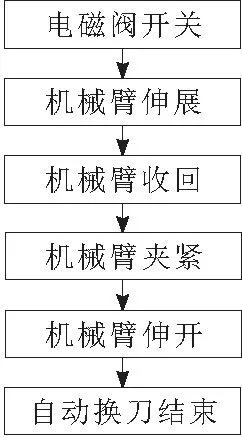
图3 自动换刀工作流程
2.2.2 断刀检测
数控机床的运行过程中,有可能出现断刀故障,在发现之后,要立刻停止机械工作,防止后续操作出现严重的安全问题。利用OC门光线的传感器,实现断刀检测。传感器的作用就是检测刀具,如发生断裂或者磨损等故障时,将实际情况发送给控制中心。若刀具发生磨损,这时控制中心则会发送停止命令,使整体机床停止工作,自动换刀,接着通知复位,最后继续工作。
2.2.3 深度检测
刀具深度的检测,是在零件加工过程中决定了加工精度以及是否可以加工。在换刀时,主轴夹紧位置,利用机械手或者人工形式,确定刀具的插入深度是否合理,是否满足零件对于加工生产的需求,并确定是否对零件的加工过程产生影响。因此,要检测刀具深度,若检测结果处于不合理状态,则需要对其重新进行调整。
2.3 系统实现平台
该软件一共分为6大功能性模块,分别为:辅助功能模块、状态显示、运行模式选取、G代码编辑、控制器的程序编辑和参数设置模块。具体软件的结构如图4所示。
通过观察图4能够看出,参数设置的模块都包含控制器参数以及主界面的参数输入。在控制器的模块编程内,利用DMC的编程指令实现软件程序的编辑,并将程序存储起来进行下载执行。然后将各个模块互相连接、互相协调,构成一个完整的机械加工整体[12-13]。
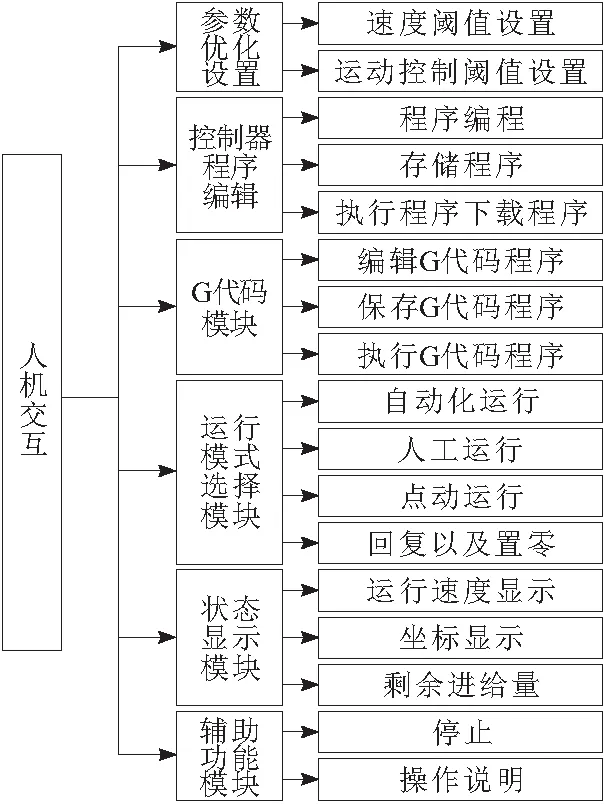
图4 数控机床控制系统的软件结构
3 实验仿真证明
3.1 仿真参数设计
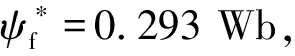
3.2 实验方法及结果分析
在速度环的非线性扩张状态中,对于观测器内参数β01、β02来说,β01在一定范围中增大,对于控制系统的性能影响比较小,在β01增大超出固定的范围以后,会引起系统的振荡发散;而β02变小超出固定的范围以后,能够令扩张状态的观测器得到对应状态的变量变差效果,而增大超出固定的范围以后,会发出高频的噪声信号,导致控制系统性能出现恶化的情况,降低超出固定范围以后,会令系统输出振荡的次数增加,同时振荡的幅度会变大。当线性的反馈参数kP过大时,振荡次数会增加,致使跟踪的速度降低。kP越大,则系统响应的速度就越快。
速度环的一阶控制器参数和位置环的控制器内相应参数,二者对于系统的影响较为类似。而控制器的其他参数则通过经验实现取值。
最终决定的速度环内参数为:β01=110,β02=80,δ1=109,b1=0.09,kP1=60。位置环内参数为:β03=110,δ2=1019,b2=0.05,kP2=19.6。
在上述设定下测试优化前后系统的响应速度,得到对比结果如图5所示。
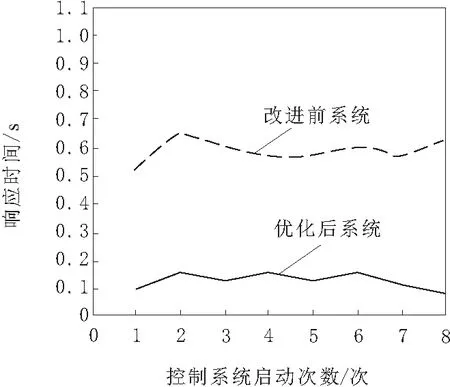
图5 系统改进前后对比结果
分析图5可知,在实验中对数控机床电气控制系统启动8次,改进前系统的平均响应时间为0.59 s,基于改进PID的数控机床电气控制系统优化设计后,该系统的平均响应时间为0.12 s,相较改进前系统有了明显提升。本文对电气负荷子系统多种事件并行处理,提升了系统处理事件的效率,并由自动换刀、断刀检测、深度检测降低损耗,降低了系统响应时间,能够有效提升数控机床运行效率。
在此基础上测试数控机床电气控制系统的控制准确性,以系统运行过程中的恒温冷却温控情况以及刀具位移变化情况作为实验指标,测试基于改进PID的数控机床电气控制系统性能。
数控机床运行过程中要实施恒温处理,实验设定数控机床恒温冷却温度为18 ℃及22 ℃,并分别采用优化前后系统对数控机床实施温度控制,测试数控机床热误差,得到实验对比结果如图6所示。
如图6所示,在恒温温度为18 ℃时,改进前系统的最大控制温度误差为0.55 ℃,平均误差为±0.45 ℃,而改进后系统的最大控制温度误差为0.10 ℃,平均误差为±0.05 ℃;同理,在恒温温度为22 ℃时,改进前系统的最大控制温度误差为0.60 ℃,平均误差为±0.40 ℃,而改进后系统的最大控制温度误差为0.20 ℃,平均误差为±0.10 ℃。分析上述实验结果可知,基于改进PID的数控机床电气控制系统通过系数法计算用电设备的电气负荷,能够使数控机床功率相对稳定,对数控机床工作温度的控制准确性更好,证明了改进PID控制系统优异的稳定性。
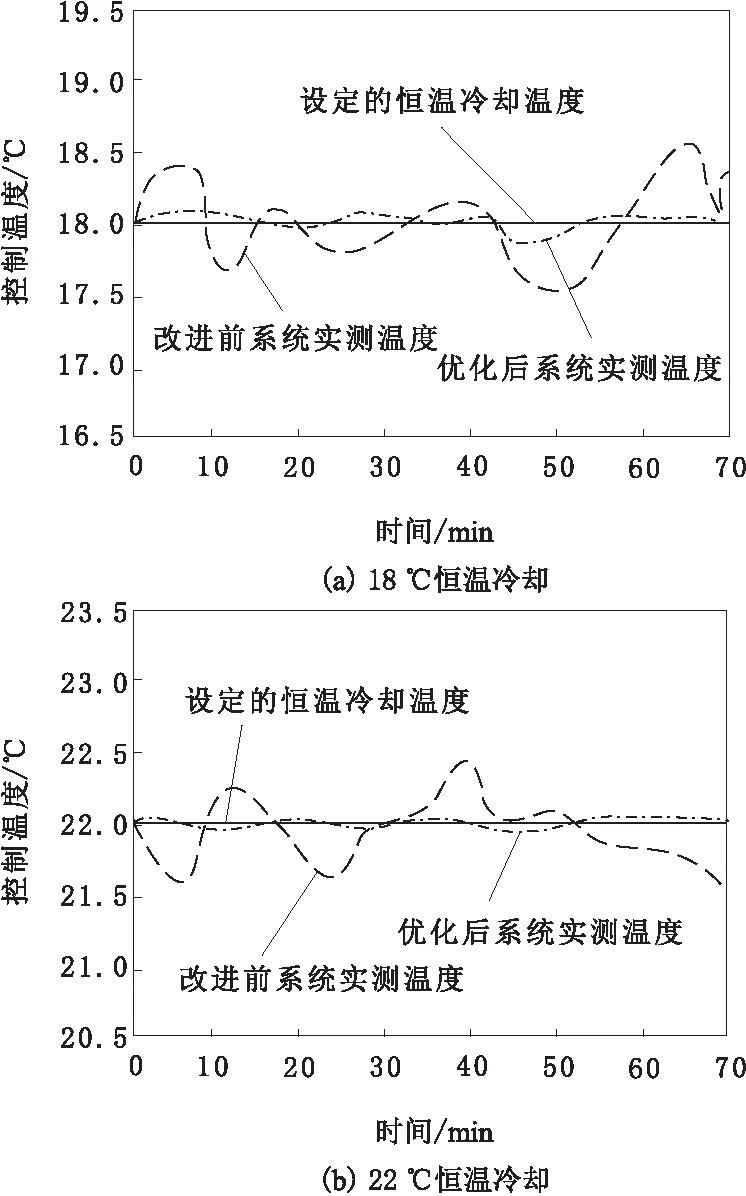
图6 系统改进前后的数控机床温度控制情况
在此基础上,测试数控机床工作中的刀具位移变化情况,实验对比结果如图7所示。
通过观察图7能够看出,未改进前系统在运行时间为1.1 s时刀具位移开始趋于稳定,但仍有小幅波动,有一定概率会损耗机床材料,降低刀口使用寿命,系统稳定性较差;反观基于改进PID的数控机床电气控制系统的刀具位移呈线性趋势上升,刀口平滑切入预设区域,没有造成材料的浪费,在运行时间为0.6 s时刀具位移开始趋于稳定,且保持平稳,说明优化后系统的控制准确性较好。本文通过PID闭环反馈系统的奈奎斯特图得出稳定的裕量信息,降低了数据采集误差,通过电气负荷子系统,降低系统模块间存在的不协调性,同时通过电源供电和直流供电子系统,使系统保持长时间极佳的稳定性。
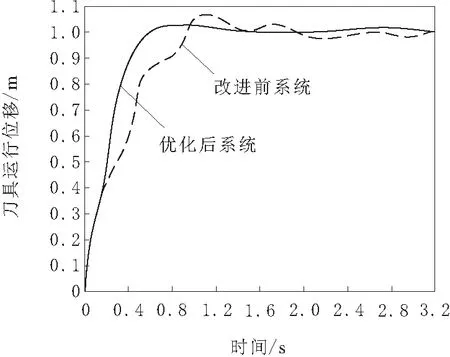
图7 系统改进前后的刀具运行位移浮动对比结果
4 结束语
本文设计了基于改进PID的数控机床电气控制系统,通过可编程逻辑控制器、数字信号处理器以及改进的PID控制方法,优化了数控机床,提升了控制系统的稳定性。
