一种自适应粒子群算法的小波神经网络优化

刘志勇，王小红

(1.咸阳职业技术学院,陕西 咸阳 712000;2.陕西省委党校,陕西 西安 710061)

0 引言

粒子群优化算法PSO (particle swarm optimization)是1995年由Eberhart和Konnedy提出的一种模拟鸟类觅食行为的优化算法[1]，该方法是以群体智能为基础，通过群体中不同个体之间的相互影响与协作，基于数学迭代方法来进行全局最优解的求解。与其他优化算法相比较，粒子群算法具有实现简单，算法收敛快，逼近能力强，而且算法精度高等特点。因此粒子群算法成为众多科研工作者研究的热点。经过多年研究，对粒子群优化算法的研究应用领域已经涉及到函数优化[2-3]、模糊系统控制[4-5]以及其他遗传算法[6-7]等。近年来，基于如何处理好控制系统解的可行性,有学者将PSO算法应用于控制系统的约束优化问题。但是，在实际工程应用中，如果对控制系统中约束条件处理不够恰当,往往会出现优化结果不收敛，或者优化结果是空集的现象。造成该结果的因素是由于粒子群算法是以数学迭代为基础的优化算法，而在算法优化的起始阶段，优化系统会随机初始化1组初始解，其次，粒子会根据一定的迭代和优化规则进行最优粒子参数更新，直至得到粒子的全局最优。而群中粒子在进行各自寻优过程中，由于没有粒子的交叉和变异，粒子寻优的整个优化过程是随机的，单个粒子在移动的过程中没有一定的方向性，进而影响了整个系统的收敛速度和精度。

本文通过引入交叉权重因子和粒子个体运动速度权值，设计了一种变权值粒子群算法，并将其应用于小波神经网络控制器，以验证该算法的有效性。

1 粒子群算法基本原理

传统粒子群算法的优化过程是来自于对觅食过程中鸟群的聚集和分散行为的模仿[8]。在现实中，鸟群觅食的关键是鸟群中个体之间的相互帮助与协作，粒子群算法的优化思路对应于鸟群的觅食过程。在粒子群优化算法中，参加求解的初始解群，类似于鸟的种群。而群中的粒子个体被看作是鸟群中的个体，粒子种群的优化过程类似于觅食过程中地点的变化。粒子群中局部最优解被视为鸟个体找到的食源，而全局最优解是整个鸟群的最优食源。在实际工程应用中，粒子群优化模型都应该存在一个多维的搜索空间和若干个参加优化的个体粒子，优化过程就是对搜索空间中粒子最优位置与移动速度的搜索与求解，其中粒子的移动速度可以决定粒子在种群中的位置和方向，而每个粒子自身的位置和速度都根据其他群中粒子经验进行调整，每个粒子的最优位置都是由粒子适应度曲线(优化函数)来决定。

在利用粒子群算法进行优化的初始阶段，粒子群体的大小、个体粒子的初始速度和位置都是随机产生。传统粒子群优化算法中，粒子的速度和位置会按照式(1)和式(2)进行更新迭代，直至找到合适的全局最优解。

v(t+1)=αv(t)+β1(p(t)-

x(t))+β2(g(t)-x(t))

(1)

x(t+1)=x(t)+v(t+1)

(2)

x(t)、x(t+1)分别为第t、t+1时刻粒子的位置；v(t)、v(t+1)分别为第t、t+1时刻粒子的移动速度；p(t)为第t时刻粒子的个体最优；g(t)为第t时刻粒子的全局最优；α为粒子的惯性权值；β1和β2为粒子的学习权值。

在式(1)中，包含着3种不同功能的公式部分：αv(t)是用来记录群中粒子的当前状态的速度，α可以用来调节粒子自身速度的惯性值；β1(p(t)-x(t))部分是粒子对自身状态的认知项，它只与粒子自身的经验值有关，是实现局部最优的基础；β2(g(t)-x(t))是粒子状态信息之间的相互合作与共享的信息项，也称之为社会项，是群中其他粒子个体运行状态的借鉴基础。3个部分在算法的优化过程中，相互平衡，相互制约，共同控制着群体、个体的运行状态优化方向。

2 VWPSO算法设计

传统粒子群算法在优化开始阶段，收敛速度性能较好，但很容易陷入局部最优解。随着优化时间推移，粒子个体移动状体信息值越来越大，求解精度与算法收敛速度变得越来越低。原因是在传统粒子群优化算法中，由于粒子在调整移动速度和位置过程中，没有准确的方向性和灵活的移动能力，粒子在寻优过程中存在着相互干扰与制约，很难在短时间内逼近各自的最优位置。鉴于传统粒子群算法存在的问题，本文通过引入粒子个体移动速度权值来扩大粒子在运动过程中的自我认知范围，使粒子在移动过程中利用更多的信息来调整各自的移动方向。

由于在粒子群中，粒子维持当前移动速度的能力影响着下一次粒子的移动方向和全体最优解。而粒子移动速度惯性权值因子α是维持粒子移动速度状态的决定性因素，它的取值直接影响着算法性能的优劣程度[9]。权值因子α值较小时，粒子群优化算法的精度较高，收敛速度较快。因此，为了提高传统粒子群算法的精度与收敛速度，将其他粒子的速度状态也作为对当前粒子速度状态优劣评价的因素，可以将粒子速度权值因子α进行重新定义为

(3)

αi(t)为第i个粒子在t时刻的惯性权值因子。根据式(3)，可以将其进一步理解为t时刻第i个粒子对整个系统的全局最优解的贡献力。根据式(1)对传统粒子群算法中全局最优解定义，进而在第i时刻粒子全局最优可以定义为

(4)

pi(t)为第t时刻第i个粒子的个体最优。针对传统粒子群算法容易陷入局部最优解的缺点，考虑将群中粒子自我的认知范围能力扩大，使其不再受限于粒子个体本身的状态经验，而是群中所有粒子的共同影响与协作下的最优自我认知范围。由此，根据群中粒子个体最优解之间的关系，可以将其重新定义为

(5)

n为粒子个数。将式(3)～式(5)代入式(1),则可以得到改进后的粒子群速度与位置的优化公式为：

(6)

x(t+1)=x(t)+v(t+1)

(7)

由式(3)可观察到，在利用优化后的粒子速度优化公式优化过程中，粒子速度的惯性权值是变化的，它会根据群中所有粒子个体的局部最优解的贡献率来进行实时调整，不再是受限于某个粒子个体的局部最优，进而解决了传统粒子群算法容易陷入局部最优的困惑，提高了算法的收敛速度。其次，在利用改写后的粒子群算法进行控制器优化过程中，为了保持优化过程中运算纲量上的统一，可以在式(7)中粒子移动速度的基础上，乘以单位时间量T，则粒子位置公式可以进一步改写为

x(t+1)=x(t)+v(t+1)·T

(8)

通过联立式(6)和式(8),可以进一步得到具有变权值粒子群优化算法模型：

(9)

x(t+1)=x(t)+v(t+1)·T

(10)

根据上述数学模型可知，改进后的变权重粒子群优化算法与传统算法相比较，变权重粒子群优化算法将中，粒子个体状态信息的最优选择，不再是受自我调节因素的影响，全局最优是整个粒子个体最优评价的加权综合。因而，其具有收敛速度快、精度高等优点。为进一步验证变权重粒子群优化算法解决实际问题的能力，本文将其应用于小波神经网络模型优化。

3 VWPSO在小波神经网络中的应用

小波神经网络WNN (wavelet neural network)是一种人工智能网络，它是在小波分析的基础上提出的[10]。WNN是在小波分析理论的基础上，利用小波变换所构造的如图1所示的一种分层多分辨率的人工神经网络模型。

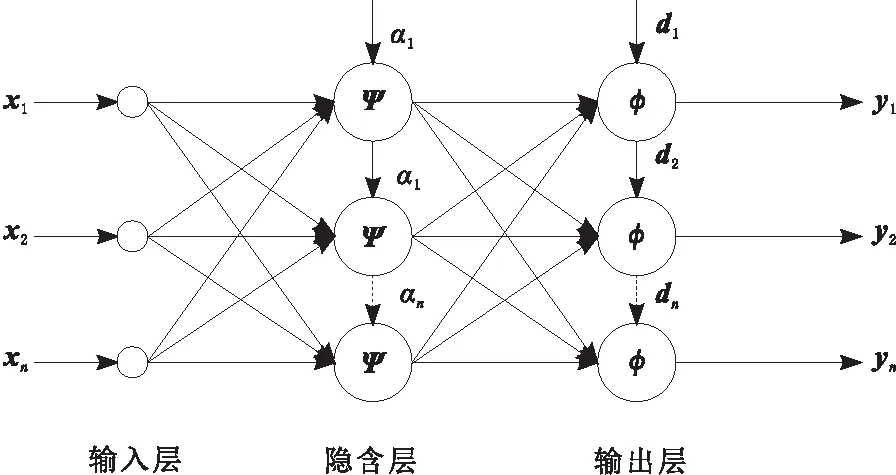
图1 小波神经网络结构

迄今为止，小波神经网络模型因其深厚的理论基础在各行业中也得到了广泛的应用，特别是在科技资讯产业领域的应用取得了丰硕的成果[11-13]。在实际工程中，小波神经网络模型也会因不同的工程领域在模型结构上也有着细微的差别与变化。目前，小波神经网络大致可分为松散型和紧密型2大类[14]，其中，紧密型神经网络处理数据的能力强于松散型网络。本文利用VWPSO算法对小波神经网络进行优化，优化过程可以描述为：在小波神经网络中，为促使全局解收敛于全局最优解，在优化过程中通过高斯函数进行参数加权，并且使输入向量的高斯加权随着算法的迭代靠近最优解的个体极值。此时，输入向量的权重越大，它们的乘积越快速地收敛至全局最优解。利用VWPSO算法对如图1所示的小波神经网络参数进行训练，训练过程如下所述。

首先，定义图1中输入层的n个输入向量为x1，x2,…,xn，则通过回溯运算可以得到小波神经网络第2层(隐含层)的第i个小波神经元的输入为

(11)

ψi为第i个小波神经元的输入。经过小波基的伸缩平移，则第3层(输出层)第i个小波神经元的输出φi可以表示为

φi=ψi(di)

(12)

di为第i个小波神经元的期望输出。则小波神经网络第i个输出yi为

(13)

根据式(13)，可以定义小波神经网络输出误差e为

(14)

根据式(3)～式(10)可以观察到，VWPSO算法在传统PSO算法的基础上加入了粒子移动速度的惯性权重因子，以及高斯加权的全局极值。进而，可以根据式(11)～式(14)来进行小波神经网络各参数的优化。具体优化步骤如图2所示。

图2 VWPSO算法优化流程

图2中，在利用VWPSO算法进行小波神经网络参数优化的过程中，首先，确定群中粒子的维数，并对群中各粒子所处位置、移动速度、惯性权值、最大迭代次数及系统误差进行初始化；其次，利用小波神经网络的回溯计算公式计算小波神经网络的实际输出及适应度值，通过计算每个粒子的全局最优来更新粒子的位置与速度。

为进一步验证VWPSO算法对小波神经网络参数优化，本文选择仿真函数解析式为

y=3cos(2x)·e-0.3x2

(15)

设定隐含层节点数m=10，粒子群种群个数为n=20，粒子速度权重初值为α∈[0.1 0.8]，粒子学习因子β1=1，β2=2，为防止粒子自我调节速度，将速度初值作如下限定：v(0)∈[0,1]。利用传统的PSO算法对小波神经网络进行优化调整，调整逼近效果曲线如图3所示，调整误差曲线如图4所示。

根据图3和图4可以观察到，利用传统的PSO算法对小波神经网络进行参数优化逼近，由于群中粒子没有自我调整能力，调整误差曲线出现了振荡，但经过20多次调整，获得全局最优解，调整误差为0.2。为验证VWPSO算法对小波神经网络优化效果，在同样仿真函数解析式下，利用VWPSO算法对神经网络参数进行优化，最终优化曲线如图5所示，VWPSO算法网络优化误差曲线如图6所示。

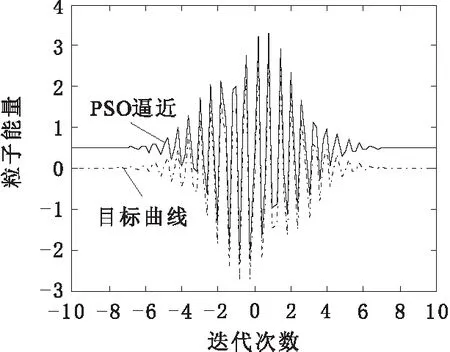
图3 PSO调整逼近曲线

图4 PSO调整逼近误差曲线

图5 VWPSO调整逼近曲线

图6 VWPSO调整逼近误差曲线

对比图3和图5可知，VWPSO由于对传统PSO中的粒子移动速度权值进行了处理，使速度权值能够进行粒子的实时状态进行调节，从而使得粒子个体状态信息能够进行最优选择，淡化了粒子自身因素的影响，提高了算法优化的收敛速度和精度。对比图4与图6可知，VWPSO算法的逼近误差精度比传统PSO算法的误差精度提高了10%，进而说明VWPSO算法不仅具有较强的曲线逼近能力，而且还具有较高的收敛精度和较快的收敛速度。

4 结束语

本文针对传统粒子群算法易陷入局部最优解的缺点，通过引入交叉权重因子和粒子个体状态最优权值，对传统PSO算法进行了改进优化。通过粒子个体状态最优权值来扩大粒子在运动过程中的自我认知范围，使粒子在移动过程中利用更多的信息来调整各自的移动方向；通过交叉权重因子提高了粒子群算法的收敛精度和收敛速度。最后，利用VWPSO算法对小波神经网络控制器进行优化，通过仿真实验有效地验证了VWPSO算法的稳定性和抗干扰性。为了提高粒子速度交叉权重因子的准确性，以后研究中可以考虑利用自组织模糊算法对其进行逼近。