一种圆柱类部件调姿的分布式并联机构误差分析
2021-08-31李维嘉李天匀刘法佑
雷 盼,李维嘉,2,刘 伟,李天匀,2,刘法佑
(1.华中科技大学船舶与海洋工程学院,湖北 武汉 430074;2.高新船舶与深海开发装备协同创新中心,上海 200240;3.渤海造船厂集团有限公司,辽宁 葫芦岛 125004)
0 引言
随着信息技术的不断前进,工业生产制造开始向自动化智能化的方向发展[1-5]。圆柱类大型零部件的对接装配一直是工业生产制造过程的重点难点,其对接质量和效率直接影响到整体生产成本和周期[6]。传统测量和对接方法存在着对接精度差、费时费力、效率低下等问题[7]。针对这一问题,刘法佑等[8]提出了一种高精度的空间装配用智能支架,该支架可实现圆柱类大型零部件的实时调姿,但没有系统地分析利用该支架进行对接装配时的误差。
由于大型零部件的作业环境往往比较复杂、现场的障碍物较多,位姿调整机构的布放精度和参数测量不可避免地会产生较大的误差。本文以船舶大型推进轴系的精确对接装配为例,建立了分布式并联机构的布放误差、参数测量误差和机构控制误差对轴系法兰位姿误差的映射模型,并分析了各误差对轴系对接精度的影响程度。
1 机构原理及组成
1.1 两点定位法
空间中任意2点可以确定1条直线的位置和姿态[9]。若将1根轴系视为1个刚体,轴系外表面的2个确定点与轴系的轴线具有确定的位姿关系,那么控制这2个确定点,就可以使轴系的轴线实现五自由度的空间运动。固定一个轴系,精确调整另一个轴系的空间位姿,就可以完成2个轴系的高精度对接。
1.2 系统组成
所采用的分布式并联调姿机构,由2个独立的三轴运动机构、2个数字式力传感器、1套六通道控制系统、1个遥控手柄和1台计算机组成。单个三轴运动机构结构如图1所示,通过高精度的伺服电机控制,可以使托块实现空间3个相互垂直方向上的精确移动。2个三轴运动机构的组合使用及精确协调控制,可以使托举的轴系实现空间的五自由度运动。托块是带有滚珠轴承的V型托块,可以使托举的轴系绕自身的回转轴转动,即保证轴系具有6个自由度的运动。数字式力传感器用于实时显示调姿机构所承受的负载大小,以判别是否超过最大载荷或发生装配干涉。
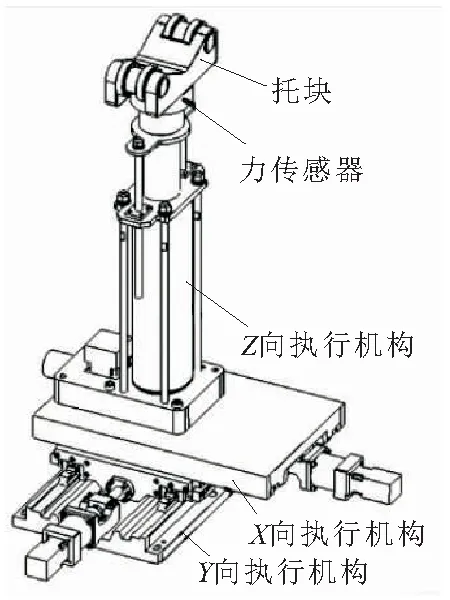
图1 三轴运动机构结构示意
2 机构误差分析
机构的误差分析主要是建立分布式并联调姿机构的输出位姿误差与机构各误差源之间的映射关系,并详细分析各误差源的影响程度,为减小系统误差和提高对接精度提供理论依据。
2.1 机构误差源分析
由于对接装配环境存在底面凹凸不平以及2个并联调姿机构独立安装的情况,因此存在机构布放误差;由于本系统需要通过常用测量工具获取一些初始参数,因此存在参数测量误差;由于机构所采用的滚珠丝杠和谐波减速器会有转动误差,因此存在机构控制误差。
2.2 误差模型建立
在对接空间建立全局坐标系O-XYZ(以下简称定系),与台体固连,记为{S};建立运动坐标系O1-X1Y1Z1(以下简称动系),与对接轴固连,记为{M}。A、B为2个电动缸轴线与轴系表面交点,O1为线段AB中点,点C为对接法兰端面圆心,如图2所示。

图2 船舶轴系对接坐标系
对接轴系的空间位姿可由动系{M}来描述,即
(1)
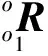
(2)
sα表示sinα;cα表示cosα;sβ、cβ和sγ、cγ以此类推。α、β、γ分别表示动系相对于定系的偏转角、俯仰角和横滚角[10]。
记A、B、C三点在定系{S}的坐标为:
(3)
(4)
(5)
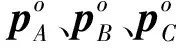
(6)
将动系{M}先绕Y1轴旋转δβ,再绕Z1轴旋转δα形成新的坐标系,记为坐标系O2,则姿态调整后C点的位置为
(7)

位姿调整后A、B两点的理论位置可求得:
(8)
(9)
2个三轴运动机构直线导轨和电动缸移动量分别为:
(10)
(11)

(12)
Cpi表示位姿调整后轴系法兰的偏移值。
姿态调整误差为
(13)
Cpt表示位姿调整后轴系法兰的曲折值。
轴系姿态调整时,旋转中心为运动坐标系原点O1。
2.3 机构布放误差的影响
进行轴系对接装配之前,需要布置好并联调姿机构。由于2个三轴运动机构布放时存在底面不平行和侧面不平行的情况,因此会导致布放误差,分别如图3和图4所示。

图3 侧面不平行

图4 底面不平行
给定机构底座间距为1 000 mm,高低差为0。根据船厂实际应用需要,轴系平动调整范围为±3.0 mm,旋转角度范围为±0.30°。选取轴系平动量,|x|=|y|∈{0.3 mm,0.6 mm,0.9 mm,…,3.0 mm},旋转角度|α|=|β|∈{0.03°,0.06°,0.09°,…,0.30°},共产生100组测量点。其中,测量点1~10、11~20、21~30、…、91~100分别为|x|=|y|=0.3 mm、0.6 mm、0.9 mm、…、3.0 mm时的结果。当机构底面夹角θ和侧面夹角ε为0.3°、0.6°、0.9°时,布放误差对轴系对接精度的最大影响如图5所示。
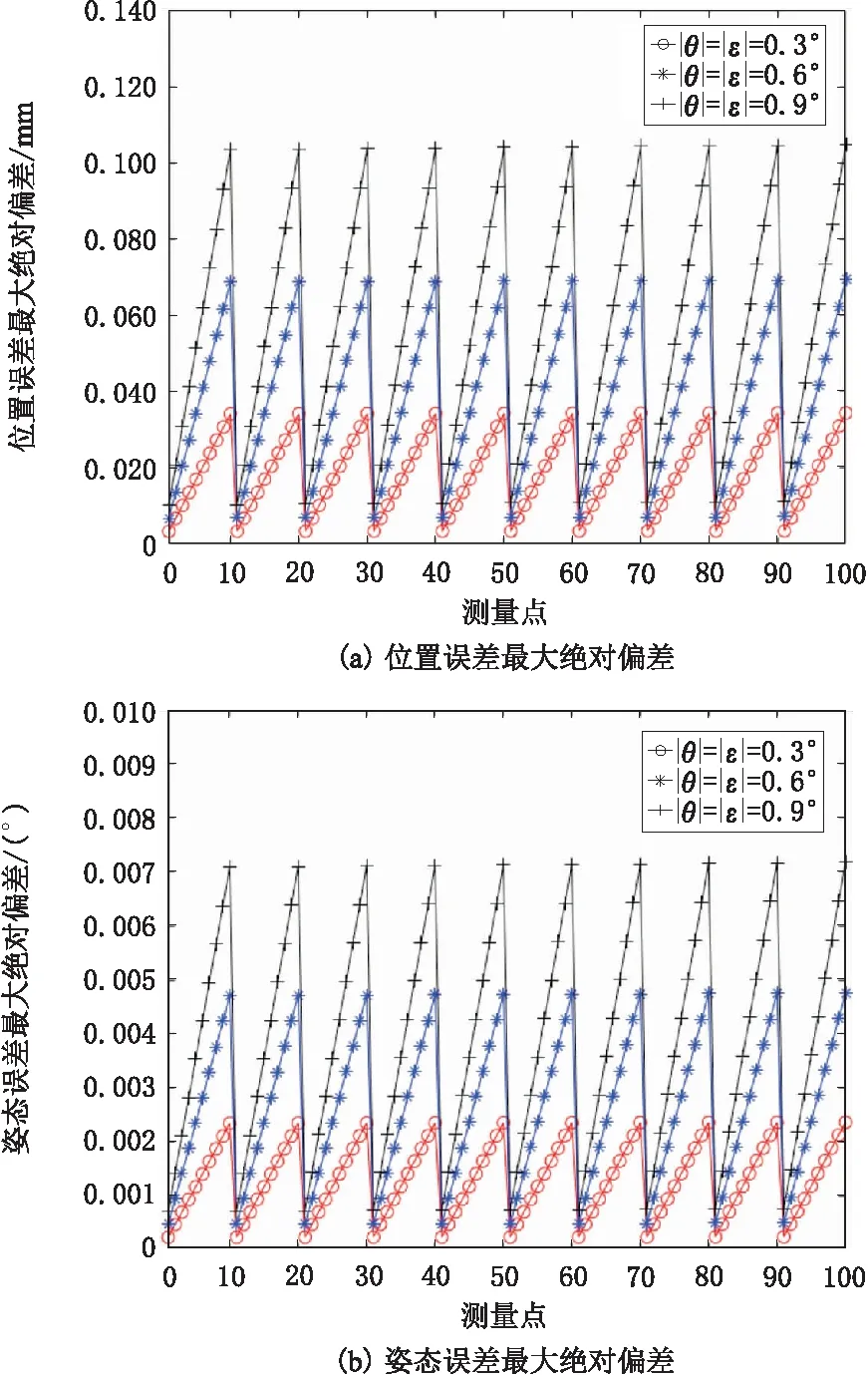
图5 布放误差对轴系对接精度的影响
根据图5可知,布放误差对轴系对接精度的影响随轴系平动量x、y的变化较小,随轴系旋转角度α、β的增大而增大,呈近似线性关系,同时,减小布放误差会显著提高轴系对接精度。机构布放误差会导致控制过程中A点和B点之间的距离发生变化,进而在轴系和机构托块之间产生滑动摩擦力,从而对机构造成损坏。经分析计算,在轴系姿态调整范围内,当机构底面夹角θ和侧面夹角ε分别为0.3°、0.6°、0.9°时,A点和B点之间距离的最大变化值分别为0.132 mm、0.265 mm、0.398 mm。该机构在垂直方向的运动控制采用的是电动缸。电动缸的缸体和活塞间、前端盖与活塞缸间均采用弹性密封圈及聚四氟乙烯导向环,可为电动缸的活塞缸提供一定的柔度,当横向受力时,单个三轴运动机构顶端允许位置偏差为0.300 mm,可以满足实际应用需要。
2.4 参数测量误差的影响
影响对接精度的测量参数主要有2个,分别是2个三轴运动机构底座水平间距L和底座高低差H。分析可知,参数测量误差只影响姿态控制精度,不会影响平动控制精度。给定机构底座间距为1 000 mm,高低差为0。选取轴系旋转角度|α|=|β|∈{0.03°,0.06°,0.09°,…,0.30°},共产生10组测量点。当底座水平间距测量误差L和底座高低差测量误差H存在如下数据关系,即L=H=1.0 mm、2.0 mm、3.0 mm时,其对轴系对接精度的最大影响如图6所示。

图6 参数测量误差对轴系对接精度的影响
由图6可知,参数测量误差对轴系对接精度的影响随轴系旋转角度α、β的增大而增大,呈近似线性关系,同时,可通过减小参数测量误差来大大提高轴系对接精度。
2.5 机构控制误差
机构控制误差主要有滚珠丝杆导程误差和谐波减速器转动误差。根据厂家提供的说明文档,滚珠丝杠转动带动物体运动600 mm时最大导程误差为0.000 9 mm;谐波减速器最大转动误差为6′,等同于每运动3 mm时最大误差为0.000 4 mm。故机构控制误差对轴系对接精度的影响可以忽略不计。
综上所述,机构布放误差对轴系对接精度的影响最大,参数测量误差次之,机构控制误差影响最小。在机构底面夹角θ和侧面夹角ε小于0.9°,底座水平间距L和底座高低差测量误差H小于3.0 mm的情况下,同时考虑机构控制误差,当轴系平动调整量|x|、|y|小于3.0 mm,旋转角度|α|、|β|小于0.23°时,轴系经过1次位姿测量和调整,即可达到对接精度要求。
3 试验结果
3.1 对接试验
由于实际船舱存在环境复杂、障碍物多以及舱底不平的情况,导致机构布放和参数测量误差偏大。本文采用质量为2 500 kg、长度为2.8 m、法兰直径为600 mm的轴系,给定机构底面夹角和侧面夹角为0.9°,底座水平间距和底座高低差测量误差为3.0 mm,搭建了船舶轴系对接试验台架,并进行了对接试验。对接试验台架如图7所示。

图7 船舶轴系对接试验台架
对接流程如图8所示。对接具体流程如下:
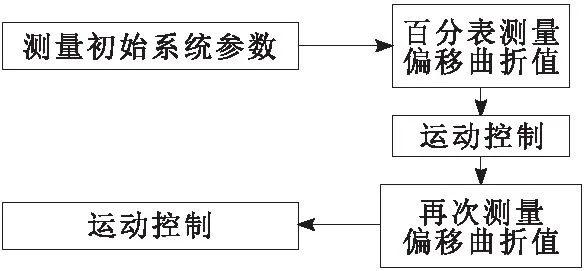
图8 船舶轴系对接流程
a.操作人员测量2组初始参数,第1组参数包括2个三轴运动机构的底座间距和高低差;第2组参数包括各直线导轨和电动缸的初始移动量,运动坐标系原点O1到法兰端面的距离及法兰直径。
b.操作人员通过按180°对称分布的2组百分表测量轴系法兰的偏移曲折值,并输入到控制界面。
c.计算机将轴系法兰的偏移曲折值转换成机构直线导轨和电动缸的移动量,然后向驱动控制系统发出控制指令,控制并联调姿机构带动轴系运动至目标位置。
d.重复步骤b和步骤c,再一次进行轴系对接,使对接精度达到要求。
3.2 试验结果
通过百分表测量轴系法兰调整前后的偏移曲折值,测量方式如图9所示。
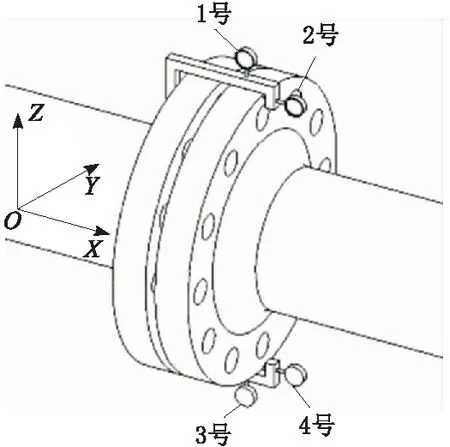
图9 测量方式
任意给定一初始位姿,按照对接流程进行对接试验。轴系法兰2次调整前后的偏移曲折值如表1、表2和表3所示。其中,记Z轴正方向为“上”,Z轴负方向为“下”,Y轴正方向为“左”,Y轴负方向为“右”。

表1 轴系第1次调整前偏移曲折值
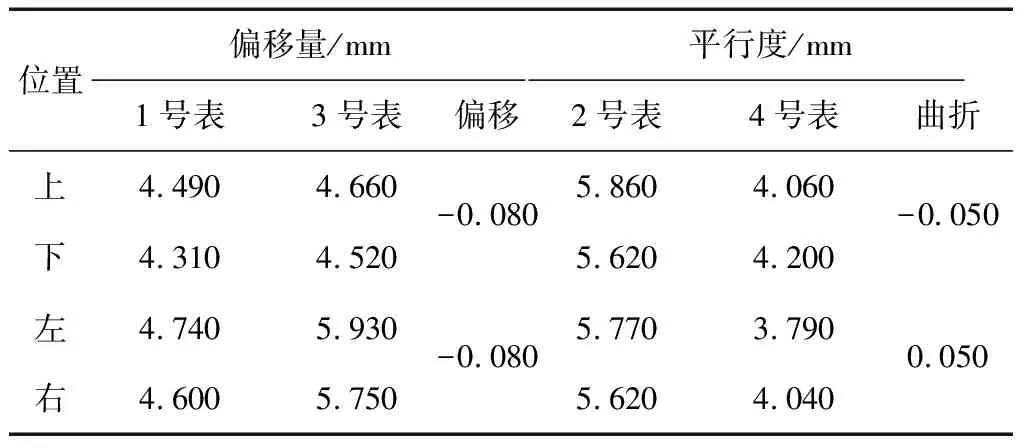
表2 轴系第1次调整后偏移曲折值
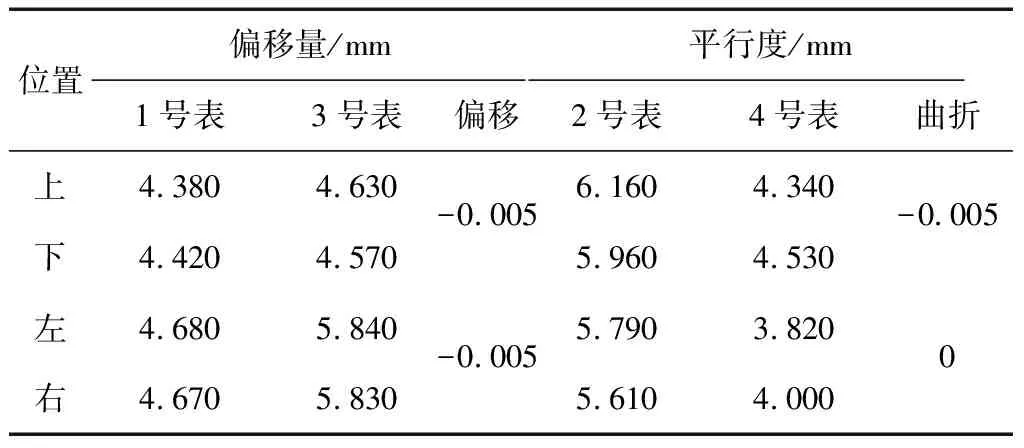
表3 轴系第2次调整后偏移曲折值
由表1可知,给定船舶轴系初始偏移为:Y轴方向,-2.780 mm;Z轴方向,2.830 mm。初始曲折为:绕Y轴,-2.630 mm/600 mm;绕Z轴,2.760 mm/600 mm。对应初始偏角为:绕Y轴,-0.251°;绕Z轴,0.264°。
由表2得知,轴系第1次调整后,偏移为:Y轴方向,-0.080 mm;Z轴方向,-0.080 mm;最大偏移为0.113 mm。曲折为:绕Y轴,-0.050 mm/600 mm;绕Z轴,0.050 mm/600 mm。对应偏角为:绕Y轴,-0.005°;绕Z轴,0.005°,最大偏角为0.007°。由2.2节中式(12)和式(13)计算得知,第1次调整后轴系偏移曲折值应为:Y轴方向,-0.082 mm;Z轴方向,-0.083 mm;绕Y轴,-0.005°;绕Z轴,0.005°。与试验结果基本一致。
表3给出了轴系第2次调整后偏移为:Y轴方向,-0.005 mm;Z轴方向,-0.005 mm,最大偏移为0.007 mm。曲折为:绕Y轴,-0.005 mm/600 mm;绕Z轴,0/600 mm。对应偏角为:绕Y轴,-0.001°;绕Z轴,0,最大偏角为0.001°。满足轴系对接偏移误差0.100 mm以内和曲折误差0.009°以内的精度要求。由2.2节中式(12)和式(13)计算可得,第2次位姿调整后轴系偏移曲折值应为:Y轴方向,-1.582×10-3mm;Z轴方向,-1.561×10-3mm;绕Y轴,-9.713×10-5°;绕Z轴,9.615×10-5°。与试验结果基本一致。
根据船厂实际应用需要,轴系平动调整范围为±3.0 mm,旋转角度范围为±0.30°。通过随机给定不同的初始位姿,进行了多次对接试验。试验结果表明,通过至多2次测量和调整,船舶轴系对接可满足精度要求,并与理论分析结果基本一致。
4 结束语
针对分布式的圆柱类大型零部件并联调姿机构,本文以船舶轴系对接装配为例,从实际应用方面分析了机构的各项误差源,建立了误差计算式。计算结果表明,机构布放误差对轴系对接精度的影响最大,参数测量误差次之,机构控制误差影响最小,且对接精度会随着机构布放误差和参数测量误差的减小而显著提高。通过多组轴系对接试验,验证了误差分析的正确性。在使用常用长度测量工具的情况下,通过合理布放机构位置,可实现1次位姿调整即可达到轴系对接位置精度0.100 mm,姿态精度0.009°。本文的研究成果为圆柱类大型零部件更高效和更高精度的对接装配提供了坚实的理论基础。
