20 kV小电阻接地系统高灵敏性接地故障检测方法

肖瑞超，李海锋，梁海锋，梁远升

(华南理工大学 电力学院，广东 广州 510641)

受弧光接地过电压、单相接地电流越限以及设备绝缘水平较高等因素的影响，近年来中性点经小电阻接地系统成为我国大中型城市配电网的主要发展趋势[1-2]。现阶段城区配电网主要以10 kV电压等级为主；然而伴随着持续增长的电力负荷水平，城区负荷密度已经达到历史高点，大量的公共土地资源被现有的变电站及馈线所占用，城区配电网的发展受到了一定的限制。为增大供电容量、扩大供电半径以及减小线路损耗，部分大中型城市率先采用20 kV电压等级作为配电电压[3]，例如：珠海横琴新区采用20 kV小电阻接地方式，广州知识城采用20 kV花瓣形接线模式，2008年浙江省建议10 kV升压改造的20 kV配电网均选择小电阻接地方式[4-5]。

单相接地故障是配电系统的常见故障[6]。在10 kV配电网中，主要采用阶段式零序电流保护解决配电系统中的单相接地故障[7-8]；而高阻接地故障主要依靠零序Ⅱ段保护动作，并且为躲开区外故障时本线路流过的对地电容电流，一般整定为60 A，其能耐受的过渡电阻值大约为100 Ω[9-10]。而在20 kV配电网中，由于通常以全电缆送电为主，供电半径更大，电缆线路更长，线路电容电流更大，其耐受过渡电阻的能力将会更差，因此无法有效切除高阻接地故障。如何有效地识别20 kV小电阻接地配电网的高阻接地故障具有重要的意义。

近年来，多种针对10 kV小电阻接地系统的保护方法相继提出。文献[11]提出一种基于故障电阻非线性识别的高阻接地故障检测算法，但对非线性特征不明显的故障难以识别。文献[12]提出一种基于零序电流波形畸变凹凸性的高阻接地故障检测方法，但其受噪声影响较大。文献[13]提出基于零序电压比率制动的接地故障保护新原理，根据零序电压自适应调整零序电流整定值，但其整定值计算复杂，可靠性不高。文献[14]结合现有零序过流保护原理，通过引入零序电压信息对零序电流测量值进行修正，各线路修正后的值与故障线路首端发生金属性接地故障时的情况相似，提高了保护的灵敏性。文献[15-16]则利用中性点电流与线路零序电流投影量之间的差异构成保护判据。上述研究都是针对10 kV系统，对于20kV小电阻接地系统的适应性还有待验证，目前相关的研究还较少。

为此，本文首先对比分析20 kV和10 kV小电阻接地系统发生单相接地故障时各线路零序电流与零序电压约束差异，进而对20 kV小电阻接地系统各零序分量之间的约束关系进行详细的分析，提出一种基于线路零序电流与母线零序电压微分值比值平均值的高灵敏性接地故障检测方法。

1 20 kV小电阻接地系统单相接地故障分析

图1为20 kV小电阻接地系统单相故障拓扑结构，图中：Hi(i=1,2,…,n)为正常线路，F为故障线路，中性点支路由曲折变压器及接地电阻Rg串接而成，假设故障发生在A相上，故障点所带过渡电阻为Rf。

图1 小电阻接地系统单相接地故障拓扑结构

图2 小电阻接地系统零序网络

首先通过简化模型(忽略线路阻抗)分析20 kV系统与10 kV系统故障特征的不同。系统的零序阻抗是由所有线路对地电容之和与变压器支路并联构成，简化后零序等效阻抗为

Z0=Zzig//ZHΣ,

(1)

其中

式中：Zzig为中性点支路阻抗；CHΣ为所有正常线路的对地电容之和；ω为基波角频率。由图2可知故障线路零序电流和母线零序电压之间的关系与中性点支路阻抗及正常线路零序电容大小有关，即

(2)

由于20 kV配电网在出线距离上与10 kV配电网有着明显的差异，且中性点接地小电阻的阻值也不一样，根据式(1)—(2)，故障线路零序电流与母线零序电压之间的相位关系也有着明显的区别。为了清晰直观地表达2种电压等级下故障线路的故障特征，通过在PSCAD/EMTDC中对简化模型的仿真得到2种电压等级配电网下故障线路零序电流与母线零序电压之间的相位差，见表1。

表1 不同电压等级下的相位关系

由表1可知，在20 kV配电网中故障线路零序电流与母线零序电压的约束关系与10 kV配电网有着明显的差异，下面将分别对20 kV小电阻接地系统正常线路和故障线路的零序电流-零序电压关系特征进行具体分析。

1.1 区外故障时本线路的零序电流电压关系

由于20 kV系统的配电线路以电缆为主，并且配电馈线较10 kV系统的距离更长，对地电容更大，同时，为了更加精确体现馈线零序电流与母线零序电压之间的关系，计及线路阻抗所带来的影响，采用π型等值线路；因此，当区外故障时，本线路的零序等值模型如图3所示，图中：u0为母线的零序电压瞬时值，i0H为正常线路的零序电流瞬时值，RH、LH、CH分别为正常线路的电阻、电感以及对地电容。

图3 正常线路的零序等值模型

为了准确分析故障稳态情况下线路零序电流的分布，从时域的角度列出零序电流的表达式，即

(3)

将式(3)两边同时与母线零序电压微分值作商，并假定在故障稳态情况下u0=Umcos(ωt+α)，i0H=ImHcos(ωt+β)，可得

(4)

由于线路的容抗远远大于感抗，线路以零序电容电流的分布为主，因此可以近似认为β≈α+90°，ImH≈ωCHUm，从而由式(4)可得

(5)

式中：o=1-0.75ω2LHCH；p=0.25ωRHCH。

下面以20 kV配电线路的典型参数为例，对o和p进行定量分析，其中CH取0.28 μF/km，而RH和LH分别取0.778 Ω/km和1.115 mH/km。图4为在线路长度变化时o和p值。

图4 线路出线长度与参数o、p的关系

由图4可见，随着线路长度的增加，o虽然有所减少，而p则有所增加，但仍然满足o≫p。因此，在一般情况下，由式(5)可知正常线路零序电流与零序电压微分值的比值由对地电容主导，并近似等于其对地电容值。其中，定义线路零序电流与母线零序电压微分值的比值绝对值为P(以下简称“比值绝对值”)。进一步对式(5)化简得到正常线路的比值绝对值

(6)

1.2 区内故障时本线路的零序电流电压关系

与区外故障不同，区内故障时流过本线路的零序电流是中性点接地支路电流与所有正常线路零序电流的矢量和，如图5所示。

图5 区内故障时零序电流分布

图5中i0g为中性点接地支路零序电流。基于上述理论，可以得到区内故障时流过本线路零序电流的时域表达式

(7)

与式(4)原理相同，由式(7)可以得到

(8)

考虑到中性点接地电阻远大于曲折变压器的零序阻抗，因此在计算中性点支路的零序电流时可以忽略曲折变压器的零序阻抗，即

(9)

将式(5)、(9)代入式(8)，可得故障线路比值绝对值

PF=

(10)

由于20 kV系统线路为全电缆线路，且较10 kV系统最大的区别在于出线距离较长，对地电容电流大，在分析区内故障时流过本线路的零序电流与母线零序电压关系时，要充分考虑系统出线长度带来的影响。下面将通过离散化计算方法对各线路比值绝对值进行分析，更加直观地区分故障线路与正常线路故障特征的差异。

1.3 故障线路与正常线路比值绝对值的关系比较

定义第q个采样点下对应的零序电流i0(q)与母线零序电压微分值u0.dif(q)的比值绝对值为P(q)，即

(11)

u0.dif(q)=f1[u0(q)-u0(q-1)].

(12)

式中f1为采样频率。

故障发生后一个周波内正常线路与故障线路的比值绝对值推导值与PSCAD/EMTDC的仿真值的变化范围如图6所示。

由图6可以看出，理论分析和仿真得到的线路比值绝对值在同一个故障工频周期下基本吻合；并且系统出线距离的增加，结合1.1节分析的o、p参数的变化，会导致故障线路比值绝对值的过零点向左偏移，其中在半周时刻会出现正常线路比值绝对值的奇异点，这是由于母线零序电压在波峰时刻采样点的微分值近似为0，会导致在这个时刻的比值绝对值突变。如何躲开此奇异点所带来的影响将在下一节的故障检测判据中予以说明。

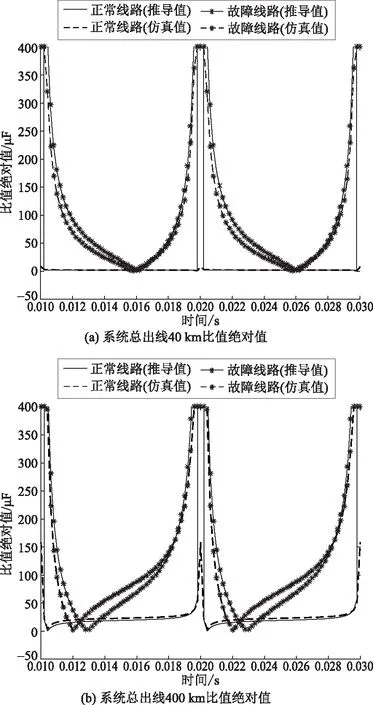
图6 不同出线长度的比值绝对值比较

2 基于零序电流-电压微分特性的故障检测方法

2.1 基本原理

通过上面的分析可知，故障线路和正常线路的比值绝对值在同一个故障工频周期内的变化范围存在明显的差异，因此通过递进式算法计算一个工频周期内的比值平均值Pave(q)，其计算公式为

Pave(q)=

(13)

式中k为数据窗的采样点数量，k=f1T，T为平均值计算的数据窗时间。

通过观察式(8)及图6可知，为了使故障线路的比值平均值输出稳定，且cot函数的周期为0.01 s，则T应该取0.01 s，对式(6)按式(13)计算发现正常线路的比值平均值Pave(q)在故障稳态时近似等于该线路的对地电容值，由于正常线路的比值会在半周时刻出现奇异点，因此设置一个比值绝对值阈值达到限制正常线路比值过大的作用；而由1.3节分析可得，故障线路的比值在绝大部分时刻都大于正常线路，因此通过递进式算法得到的故障线路比值平均值PaveF(q)也将明显区分于正常线路。

2.2 检测算法流程图

由于在故障发生时，母线零序电压会出现突变，因此本文提出的检测算法以零序电压的突变量作为启动判据，进而对所有馈线的零序电流和母线零序电压进行低通滤波并采样，以半个周波为数据窗计算所有线路的比值平均值，最后以比值平均值的大小对故障线路进行检测。具体检测算法流程如图7所示。

图7 检测算法流程

2.3 整定原则

本文所提的基于零序电流与零序电压微分比值平均值的检测算法要通过整定以下参数来实现：

a)零序电压突变整定值u0.set。本检测算法是以零序电压突变量作为启动判据的，所以在设置零序电压突变整定值u0.set时要考虑在高阻接地故障中零序电压的大小及采样频率的大小，同时在故障暂态过程中，零序电压存在一定的震荡，所以u0.set取5 V。

b)比值平均值计算时间窗T。因为考虑到故障线路中比值绝对值主要部分由cot函数构成，周期为0.01 s，因此在计算比值平均值时设计数据处理的时间窗长度为0.01 s，即半个周波，这样输出的比值平均值波形较为平稳。

c)比值绝对值阈值Pmax。设置比值绝对值阈值的主要目的是为了躲开在半周时刻出现奇异点带来的影响，即减弱非故障线路比值平均值超调量过大导致检测误判的可能性。考虑比值绝对值阈值的增加不过分影响故障线路的比值平均值，可取2倍的故障线路比值平均值的稳态值，本文取比值绝对值阈值Pmax为400 μF。

d)保护动作整定值Pact。为了验证该检测算法在20 kV配电网系统中的可靠性，假设系统带5条出线100 km的全电缆线路，其单位长度对地电容为0.28 μF/km，根据式(13)可知，正常线路比值平均值PaveH≈28 μF，因此保护整定值的选取应该按照正常线路比值平均值的最大值来整定。

考虑短路故障暂态特征对比值平均值的影响，保护动作整定值Pact的计算公式为

Pact=KrelCHmax×106.

(14)

式中：Krel为可靠系数，一般取1.5～2；CHmax为单条馈线最大对地电容。

因此，以某100 km的馈线为例，根据式(14)计算得Pact可取42～56 μF。为了方便保护的定值整定，可以统一将保护动作整定值定为60 μF。

3 仿真验证

仿真模型依托的20 kV小电阻接地系统如图1所示，其中曲折变压器按照其结构原理搭建相应PSCAD模型[17]，母线上接有5条型号均为ZR-YJV22-18-20kV-3×400的电缆线路，分别按照其尺寸结构[18]搭建相应的集中参数模型，其电气参数见表2。

表2 ZR-YJV22-18-20 kV-3×400电缆电气参数

3.1 本文所提方法的性能测试

为了验证本文所提故障检测方法的有效性，设置3组出线总长度分别为50 km、100 km以及300 km的仿真，对应每种情况下的每条馈线长度按照等比例变化。其中在50 km系统中馈线1至馈线5的长度分别为3 km、8 km、12 km、16 km以及11 km。换算到20 kV侧的系统等效阻抗和主变压器漏抗之和为0.73 Ω，接地小电阻为20 Ω，采样频率为2 kHz。

选择馈线3作为故障线路，以馈线4作为观察样本，分别在故障线路的首端、中点及末端设置经线性过渡电阻、金属性接地和电弧接地的单相故障。

电弧模型采用控制论电弧模型，其电弧方程为

(15)

(16)

式(15)—(16)中：gArc为电弧电导；G为电弧稳定电导，初始值为1 000 S；C为时间常数；电弧弧长lArc取100 cm；γ为经验系数，一般取2.85×10-5；imax为电弧电流幅值，近似取电弧故障点直接接地时的电流峰值[19]；iArc为瞬时电弧电流；稳态电弧电压梯度Vp取17 V/cm[20]。

通过仿真对比故障线路和正常线路的比值平均值大小以及保护动作情况，来验证本检测算法的有效性。

表3和表4分别给出了线性过渡电阻故障以及电弧故障时故障线路和正常线路的比值平均值的仿真结果以及保护动作情况。

表3 线性过渡电阻故障时馈线的比值平均值以及保护动作情况

表4 电弧故障时馈线的比值平均值以及保护动作情况

图8为系统总出线长度50 km时，金属性故障和经1 000 Ω线性过渡电阻故障情况下各馈线比值平均值的变化范围。图9为系统总出线长度300 km时，金属性故障和经1 000 Ω电弧过渡电阻故障情况下各馈线比值平均值的变化范围。

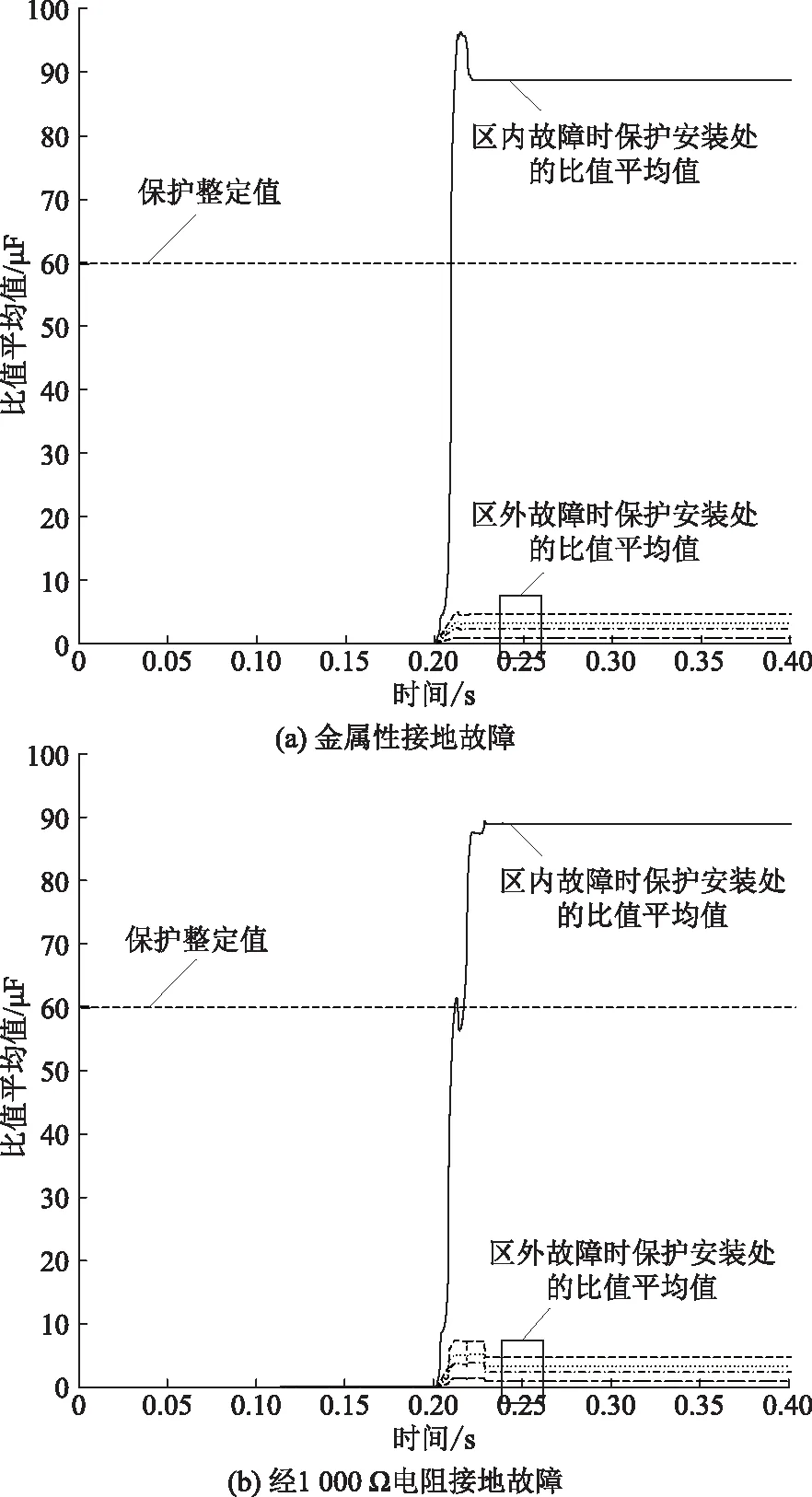
图8 系统总出线50 km时比值平均值的变化曲线

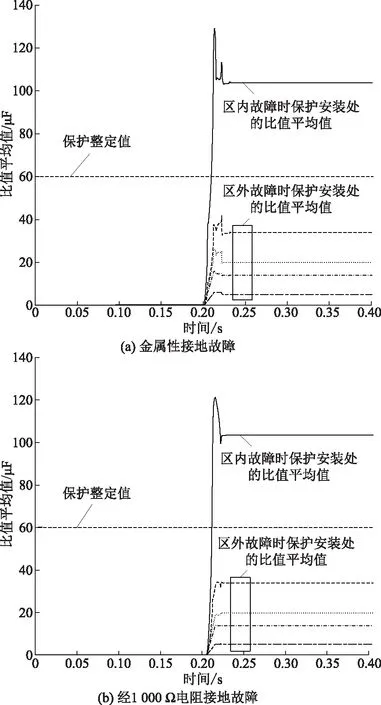
图9 系统总出线300 km时比值平均值的变化曲线

综合分析得到如下结论：

a)区内故障情况下，接地电阻在0～1 000 Ω的检测范围内，Pave在故障后约10 ms(即半个周波)达到整定值，并在之后始终大于故障检测整定值，均能可靠动作；并且在动作范围内，受过渡电阻大小的影响很小，对于小电阻接地故障和高阻接地故障均具有较好的检测灵敏度和可靠性。

b)区外故障时，Pave始终小于故障检测整定值，并近似等于本线路对地电容的大小，即与本线路的出线长度有关；当线路出线较长时，Pave也会相应增大，但是依然小于检测整定值且具有足够的裕度，保护均不动作，具有良好的选择性。

c)根据电网运行的需求，改变配电系统的出线规模，本文所提高灵敏性故障检测方法在短距离送电与长距离送电中均具有良好的适应性，且能有效识别线性过渡电阻故障以及非线性电弧故障。

3.2 与传统故障检测方法对比

阶段式零序电流保护是目前中性点经小电阻接地系统应对接地故障的常规方法。其中零序Ⅱ段整定值的设置需躲开本线路流过的最大对地电容电流，一般整定为60 A。

为了验证本文所提检测方法相比于传统方法的优越性，以馈线3中点发生单相接地故障为例，对不同过渡电阻情况下接地故障进行仿真分析。其中，系统出线总长度为50 km时，过渡电阻分别取0、50 Ω、100 Ω、500 Ω和1 000 Ω，具体的测试结果见表5。

表5表明，当过渡电阻低于100 Ω时，2种故障检测方法均能可靠识别故障，而当过渡电阻大于100 Ω时，传统故障检测方法已经无法检测出接地故障，而本文所提的方法依然能够有效识别接地故障，其灵敏性要远远高于传统方法。

表5 与传统故障检测方法对比的测试结果

4 结论

针对现有城市配电网的故障检测与保护都是基于10 kV展开，并且在小电阻接地系统中难以识别高阻接地故障的现象，本文提出一种适用于20 kV小电阻接地配电网的高灵敏性接地故障检测方法，根据各出线零序电流与母线零序电压微分值离散化的比值平均值大小检测故障发生与否，并给出具体的整定原则。本文所提方法仅依靠线路零序电流与母线零序电压之间的约束关系，原理简单，物理概念清晰；基于PSCAD/EMTDC的大量仿真验证表明本文所提方法对于区内故障具有较高的灵敏性，对于各类过渡电阻的检测能力可达1 200 Ω，且所需采样频率不高，易于工程实现。