粗糙度对水汽在细颗粒表面异质核化影响的数值模拟
2021-08-31熊桂龙谢静雯杨林军
熊桂龙,谢静雯,杨林军
(1南昌大学资源环境与化工学院,江西南昌 330031;2南昌大学鄱阳湖环境与资源利用教育部重点实验室,江西南昌 330031;3东南大学能源热转换及其过程测控教育部重点实验室,江苏南京 210096)
引 言
细颗粒物已成为大气的主要污染物之一,其不仅造成雾霾、酸雨等环境污染,还对人体健康带来严重危害[1-3]。由于燃煤烟气中细颗粒物粒径小、数量多,传统除尘设备如静电除尘器、袋式除尘器等不易对其高效脱除[4];采用水汽相变、声聚并、电聚并、磁聚并、光聚并、化学团聚等作用使其长大为粗大颗粒物[5-10],是促进其高效脱除的重要预处理措施,其中水汽相变技术具有较好的工程应用潜力,其主要机理为:在过饱和水汽环境中,水汽分子在细颗粒物表面发生异质核化凝结,使细粒子长大成较大的含尘液滴,从而使颗粒粒度增大、质量增加,易受惯性冲击而被传统除尘器高效捕集[11-12]。水汽在细颗粒表面发生凝结长大主要分为两个阶段:首先是异质核化阶段,水汽分子在细颗粒表面发生异质核化,形成液滴晶核;然后是自发凝结长大阶段,水汽在液滴晶核的表面自发进一步凝结长大,形成以细颗粒为核心的含尘液滴。其中,异质核化阶段是决定水汽在细颗粒表面是否发生异质凝结的关键步骤。
国内外对水汽相变的研究已有较长的历史,目前应用较多的理论是Fletcher经典异质核化理论[13],其易求得成核特性参数,但忽略了一些影响因素,与真实情况误差较大,有不少学者对其进行了改进。Hienola等[14]基于正壬烷、正丙醇及其混合物在三种不同尺寸银粒子上的非均相成核的实验研究结果,认为线张力对异质核化过程有重要影响,是造成微观接触角与宏观接触角不同的主要原因。Singha等[15]和Iwamatsu[16]提出在固-液-气三相接触线上由于分子间的相互作用,会产生过剩的自由能,因此在三相平衡系统中线张力被定义为固-液-气三相接触线上单位长度的自由能。Luo等[17]认为实际情况中促进液滴晶核生长的机制有两种,除了Fletcher经典核化理论中考虑的水汽分子直接蒸汽沉积机制,还有水汽分子的表面扩散机制,并推导出了蒸发系数及液滴晶核长大速率方程。Fan等[18]综合考虑了液滴晶核的两种生长机制、簇平衡数密度的自洽表达式和线张力的影响,推导了不溶性球形粒子稳态非均相成核速率的修正表达式。熊桂龙等[19]基于分子动力学理论对水汽在细颗粒表面异质核化的特性进行了研究和分析。Heidenreich等[20]基于渣颗粒、石英颗粒和石蜡油颗粒在蒸汽中核化凝结的实验结果,研究后认为颗粒表面越粗糙,其成核临界饱和度越小。凡凤仙等[21]利用自仿射分形理论描述粗糙颗粒表面,探讨研究了可溶性盐含量和表面粗糙程度对过饱和水汽在细微颗粒表面异质核化特性的影响。Fan等[22]提出了颗粒粗糙度因子的概念并对Young方程进行了修正,考察了颗粒粗糙度和润湿剂对异质核化的影响。
已有的相关研究大多是将细颗粒视为光滑表面且没有考虑水汽分子的表面扩散作用,因此,本文基于Fletcher经典核化理论,综合考虑了液滴晶核的两种生长机制(水汽分子直接蒸汽沉积机制与水汽分子的表面扩散机制)、线张力、线粗糙度因子、表面粗糙度因子的影响因素,建立了水汽在粗糙表面细颗粒上异质核化的理论模型,进一步分析了线粗糙度因子、表面粗糙度因子对异质核化特性的影响规律,为水汽相变技术促进燃煤烟气中细颗粒物脱除提供理论基础与参考。
1 水汽在粗糙表面颗粒上的异质核化模型
在过饱和水汽环境中,水汽在粗糙表面颗粒上的异质核化过程十分复杂,为了方便研究,假设细颗粒为不可溶性的粗糙表面颗粒,水汽在颗粒表面凝结形成的液滴晶核为球冠状,并且忽略液滴晶核之间的相互作用。水汽分别在光滑颗粒与粗糙颗粒表面上发生异质核化过程的示意图如图1所示。图1中R为颗粒的半径,r为液滴晶核的半径,d为液滴晶核中心与颗粒中心的距离,ψ为液滴晶核中心和颗粒中心连线与液滴晶核中心和三相接触线上的点连线之间的夹角;φ为液滴晶核中心和颗粒中心连线与颗粒中心和三相接触线上的点连线的夹角;θ为液滴晶核与颗粒的接触角。

图1 水汽在光滑颗粒和粗糙颗粒表面异质核化过程示意图Fig.1 Schematic diagramof heterogeneous nucleation of water vapor on smooth and rough surfaceof particles
对于光滑表面的球形颗粒,固-液-气界面满足Young方程[12]:
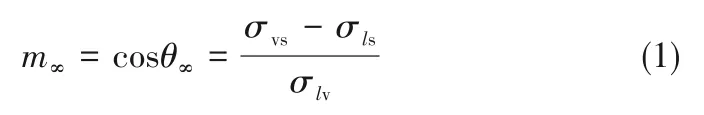
式中,m∞为宏观接触角的余弦值;θ∞为液滴晶核与颗粒之间的宏观接触角;σls,σlv,σvs分别为液-固、液-气、气-固的界面自由能,其具体取值参见文献[12]。
在固-液-气三相接触线上由于分子间的相互作用,会产生过剩的自由能,因此在三相平衡系统中线张力被定义为固-液-气三相接触线上单位长度的自由能[15-16]。由于线张力的存在会间接地引起接触角的变化,而Young方程中的宏观接触角忽略了线张力的作用。因此,考虑线张力对接触角的影响,通过受力分析,建立固-液-气三相界面平衡方程,经推导得到修正后的Young方程如下[19]:
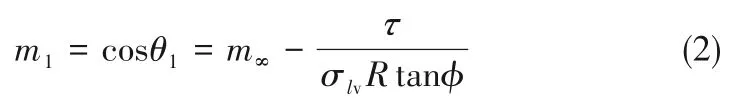
式中,m1为考虑线张力后的接触角余弦值;θ1为考虑线张力后的液滴晶核与颗粒间的接触角;τ为三相线张力。根据已有的相关文献,线张力数量级的取值范围约在10-12~10-10[15],因此在本文的模拟计算中,线张力取τ=-1.1×10-11N[5]。
实际工业过程中,燃煤细颗粒表面通常是粗糙的,而粗糙度对水汽在细颗粒表面异质核化行为具有重要影响,因此,考虑了线张力与颗粒粗糙度后,需对Young方程做进一步的修正[22]:

式中,m为微观接触角的余弦值;θ为液滴晶核与颗粒间的微观接触角;φs为颗粒的表面粗糙度因子,其定义为粗糙粒子与光滑粒子的固-液界面面积比;φl为颗粒的线粗糙度因子,其定义为粗糙粒子与光滑粒子的固-液接触线的长度比。根据已有的相关文献,细颗粒粗糙度因子的取值范围约在1.0~3.0[22]。
由图1可知,理论模型的几何参数关系计算如下:
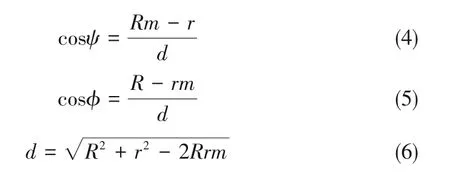
气-液、液-固的接触界面面积及三相接触线的长度计算如下:
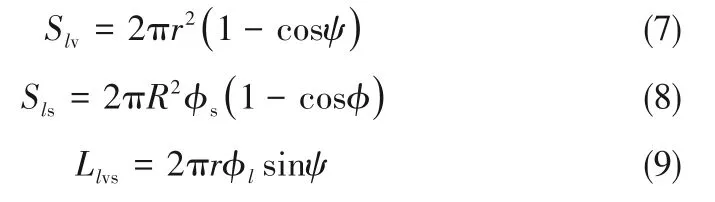
通过计算以O'为球心,r为半径的球体的体积与其被细颗粒包围部分的体积之差可得到球冠状的液滴晶核的体积为:
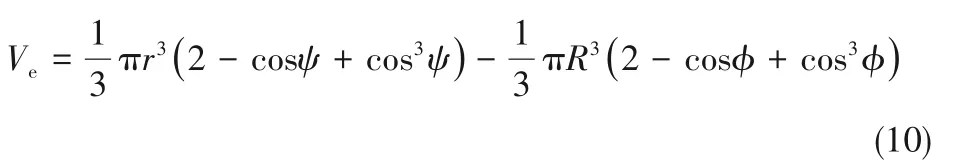
式(7)~式(10)中,Slv为液-气接触面面积;Sls为液-固接触面面积;Llvs为液-气-固三相接触线的长度;Ve为液滴晶核的体积。
本文在考虑了线张力的作用后,成核自由能的计算在Fletcher经典核化理论基础上增加了线项。在等温、等压条件下,蒸汽在颗粒表面发生异质核化,系统吉布斯自由能G为胚胎滴自由能、过饱和水汽自由能、界面自由能及三相线上自由能的总和。当水汽在细颗粒表面发生核化凝结,形成一个液滴晶核时,系统的吉布斯自由能变化量ΔG为[13-14]:
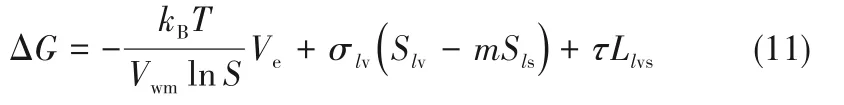
式中,kB为Boltzmann常数,取1.38×10-23J·K-1;T为水汽的温度;S为水汽的过饱和度;Vwm为一个水分子的体积,取2.99×10-29m3。
当ΔG达到极大值时,由ΔG对r求导并令其为零,可得到临界液滴晶核半径r*和临界成核自由能ΔG*为:
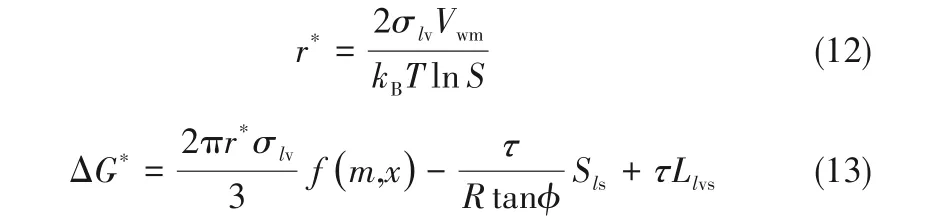
式中,f(m,x)为形状因子,由颗粒的性质决定,根据Fletcher经典核化理论[23],其计算如下:

在Fletcher经典核化理论中,认为水汽在细颗粒表面的凝结长大仅仅由气相水汽分子直接扩散到细颗粒表面发生凝结,进而使液滴晶核发生凝结长大;而根据分子动力学理论,在过饱和水汽环境中,液滴晶核的凝结生长有两种机制:一种是水汽分子直接沉积机制,其原理是由于水汽的蒸气压较大,蒸汽中的水分子会直接凝结到液滴晶核表面发生凝结长大;另一种是水分子的表面扩散机制,其原理是由于水分子的表面扩散能大于吸附能,吸附在细颗粒表面的水分子会扩散至液滴晶核表面发生凝结长大[24]。同样,液滴晶核表面蒸发过程也是由这两种机制共同作用的,液滴晶核表面的凝结和蒸发过程,最终会达到动态平衡。图2所示为水汽分子在细颗粒表面运动过程示意图,图2中,Bg为含g个水分子的球形帽状团簇;α为水汽分子直接扩散角;β为水汽分子表面吸附扩散角;Cg(α)为水汽分子直接沉积凝结速率;Cg(β)为水汽分子表面扩散凝结速率;Eg(α)为水汽分子直接蒸发速率;Eg(β)为水汽分子表面扩散蒸发速率。
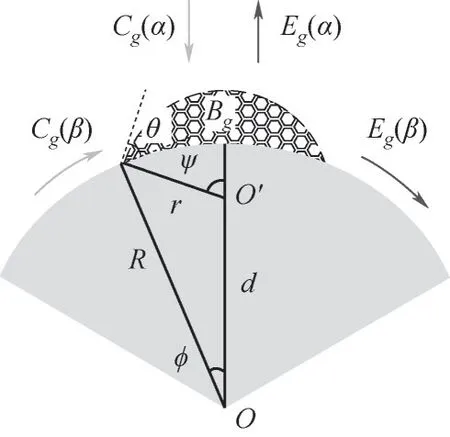
图2 水汽分子在细颗粒表面运动过程示意图Fig.2 Schematic diagram of water vapor molecules moving on the surface of fine particles
由图2可知,水汽分子在细颗粒表面的凝结速率主要由水汽分子直接蒸汽沉积速率Cg(α)和水汽分子表面扩散速率Cg(β)构成,因此,凝结速率Cg为两种机制的加成:
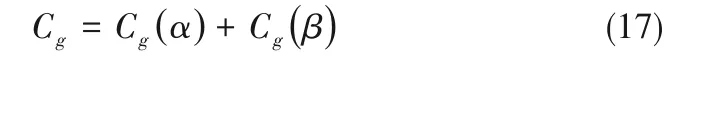
当水汽在细颗粒表面发生凝结长大时,水汽分子通过直接沉积的方式添加至液滴晶核表面,即直接蒸汽沉积速率Cg(α)为[25-28]:
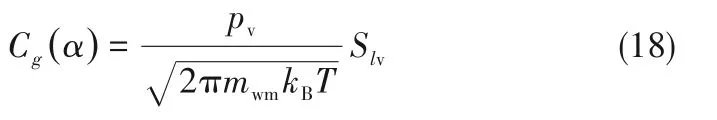
当水汽在细颗粒表面发生凝结长大时,水汽分子通过表面扩散的方式扩散至液滴晶核表面,即表面扩散速率Cg(β)为[25-28]:
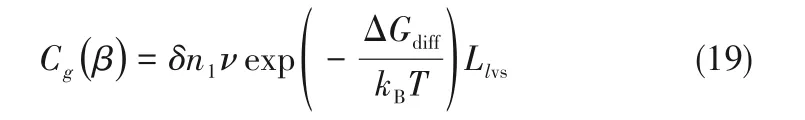
式中,pv为蒸汽的压力;δ为一个水分子的平均跳跃距离,取0.32 nm[24];ν为表面水分子的振动频率,取1013s-1[29];mwm为一个水分子的质量,取2.99×10-27kg;ΔGdiff为每摩尔水分子在细颗粒表面扩散时的表面扩散能,取2.99×10-21J·mol-1[30];n1为细颗粒表面吸附的水分子密度,其计算如下:
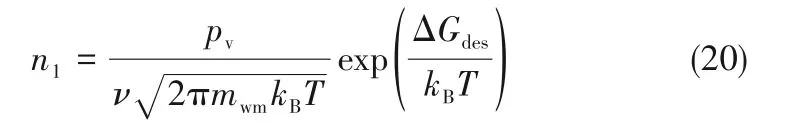
式中,ΔGdes为每摩尔水分子在细颗粒表面的解吸能,约为表面扩散能的1/10,取2.99×10-20J·mol-1[30]。
由饱和状态下气-液界面达到平衡时的相平衡法求得的两种蒸发速率为[24]:

在考虑了线张力、颗粒粗糙度、水汽分子在颗粒上直接蒸汽沉积机制和表面扩散机制等影响因素的共同作用下,在单位时间内,水汽在细颗粒表面核化凝结形成的液滴晶核数量,即成核速率J的表达式为[17]:
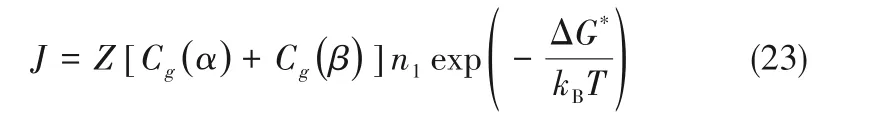
式中,Z为Zeldovich因子,Vehkamäki等[31]通过推导计算得到了水汽在球形细颗粒上核化凝结时Z的表达式如下:

基于以上方程,本文采用数值模拟的方法,通过MATLAB软件建立数学模型并进行编程,对水汽在粗糙表面的细颗粒上发生异质核化的特性参数进行分析与讨论。
2 结果与讨论
2.1 基于不同理论模型的临界过饱和度
为了准确描述水汽分子在细颗粒物表面异质核化特性,基于Fletcher经典核化理论,考虑水汽分子的表面扩散机制、线张力、颗粒粗糙度等作用,采用四种改进的不同理论模型,分别计算了水汽在SiO2和TiO2细颗粒物表面发生异质核化的临界过饱和度;并将模拟计算结果与Chen等[32-33]的实验(实验条件:SiO2和TiO2细颗粒物的宏观接触角分别为20°和16°,粒径为0.015~0.12μm,过饱和水汽环境的温度为308 K)研究结果进行对比,图3所示为基于不同理论模型的临界过饱和度随细颗粒物粒径变化的规律。
由图3可知,随着细颗粒物粒径的增大,水汽在细颗粒物表面发生异质核化凝结所需的临界过饱和度减小,这说明在温度、宏观接触角、水汽过饱和度等条件相同时,细颗粒物的粒径越大,水汽分子越容易在其表面发生异质核化凝结,形成液滴晶核。
从图3可以看出,对于粒径为0.12μm的SiO2颗粒和TiO2颗粒,其表面发生异质核化凝结的临界过饱和度的实验值分别为1.013和1.010,均小于1.1。也就是说,对于亚微米级的细颗粒物来说,在较低的过饱和水汽环境中,即可实现水汽分子在其表面发生异质核化凝结长大。
从图3还可看出,与基于Fletcher经典核化理论的其他模型相比,当τ=-1.1×10-11N,φl=φs=1.1时,基于Fletcher经典核化理论并同时考虑了水汽分子表面扩散机制、线张力和颗粒表面粗糙度影响的理论模型计算得到的结果更接近Chen等的实验研究结果,这说明水汽分子的表面扩散机制、线张力、粗糙度对过饱和水汽在细颗粒物表面发生异质核化凝结有重要影响,同时考虑了这三种作用后的异质核化理论模型可以较好地计算临界过饱和度,因此,本文后续的计算都是基于此种理论模型进行的。
2.2 粗糙度对临界成核自由能的影响
临界成核自由能ΔG*是指系统的吉布斯自由能ΔG随液滴晶核半径r的增加而增加,当达到极大值时系统的自由能。根据Fletcher经典成核理论,液滴晶核形成的可能性取决于系统的吉布斯自由能ΔG的变化,当达到极大值ΔG*时,液滴晶核就会越过成核自由能势垒,形成临界液滴晶核,此后即转入自发凝结长大的过程。因此,临界成核自由能的存在是蒸汽凝结必须经过核化的原因,它反映了水汽的成核能力,在一定的过饱和度情况下ΔG*越小,水汽在细颗粒表面就越容易发生核化。
图4所示为在温度为298.15 K、宏观接触角为50°时,在不同线粗糙度因子和表面粗糙度因子下临界成核自由能随颗粒粒径的变化规律。
由图4可知,对于光滑表面和粗糙表面的细颗粒,随着细颗粒粒径的增加,临界成核自由能都是逐渐减小的。对于粒径为0.01~0.1μm的细颗粒,随着颗粒粒径的增加,临界成核自由能明显减小;对于粒径大于0.1μm的细颗粒,随着颗粒粒径的增加,临界成核自由能逐渐减小并趋于平缓。
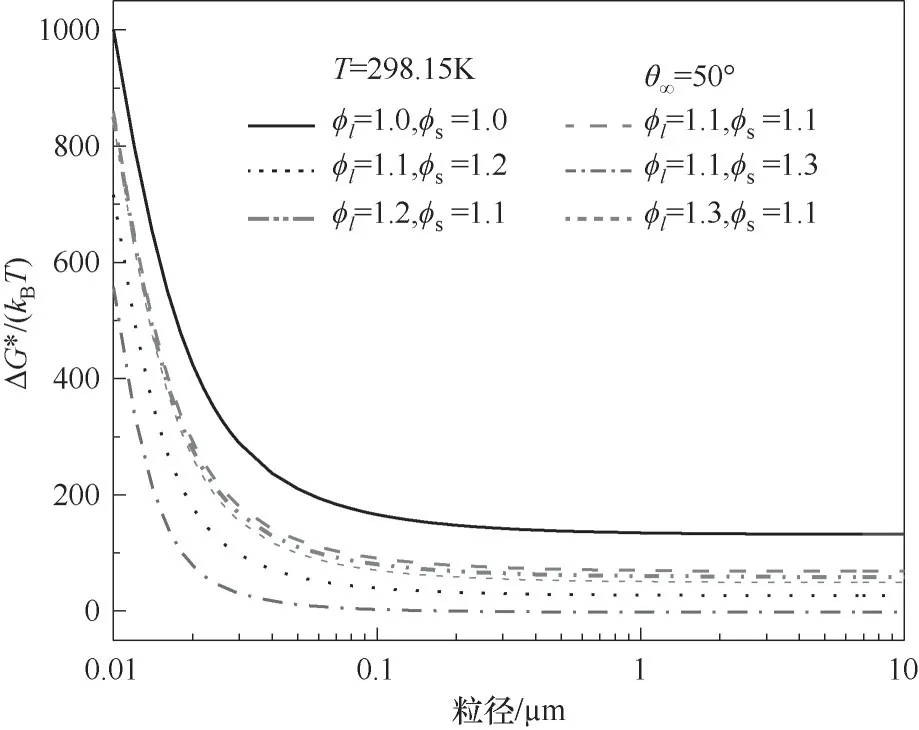
图4 不同粗糙度因子下临界成核自由能随粒径的变化规律Fig.4 The free energy of critical nucleation varies with particle size under different roughness
从图4可看出,与粗糙表面的细颗粒相比,光滑表面(φl=φs=1.0)的细颗粒,其发生异质核化所需的临界成核自由能是最大的,这说明颗粒的粗糙度对于临界成核自由能有重要影响。无论是增大线粗糙度因子还是表面粗糙度因子,临界成核自由能均减小,这说明适当增大细颗粒的粗糙度,可以降低成核势垒,有利于发生异质核化。特别地,当φl=1.1,φs=1.3时,对于粒径大于0.1μm的细颗粒,临界成核自由能为负,这说明在此条件下蒸汽在细颗粒表面的异质核化可以自发地发生。
从图4还可看出,与颗粒的线粗糙度因子相比,颗粒的表面粗糙度因子对临界成核自由能的影响更为明显,如对于0.1μm的颗粒,当φl=1.1,φs=1.1时,临界成核自由能为78.566kBT;当φl=1.1,φs=1.2时,临界成核自由能为32.336kBT;而当φl=1.2,φs=1.1时,临界成核自由能为68.604kBT。这说明增大表面粗糙度因子比增大线粗糙度因子后所计算的临界成核自由能更小,这主要是因为较大的线粗糙度因子意味着较长的三相接触线周长,从而增加了系统吉布斯自由能中的线项;较大的表面粗糙度因子则意味着较大的颗粒表面积,从而增加了蒸汽分子与细颗粒之间的接触界面面积。
2.3 粗糙度对成核速率的影响
成核速率J是指在单位时间、单位体积内过饱和水汽在单个细颗粒表面上发生异质核化时形成的液滴晶核数量。在过饱和水汽环境中,水汽在细颗粒表面凝结形成液滴晶核,当液滴晶核的半径达到临界半径r*时,只需再捕获一个水分子即可自发地发生凝结长大。因此,成核速率是重要的核化特性参数,对水汽在细颗粒表面发生异质核化凝结具有重要影响。过饱和水汽在单个细颗粒表面上发生异质核化时,单位时间内形成临界尺寸r*晶核液滴的数量称为成核速率。
图5所示为在温度为298.15 K,宏观接触角为50°,细颗粒粒径为1μm时,在不同线粗糙度因子和表面粗糙度因子下成核速率随过饱和度的变化规律。
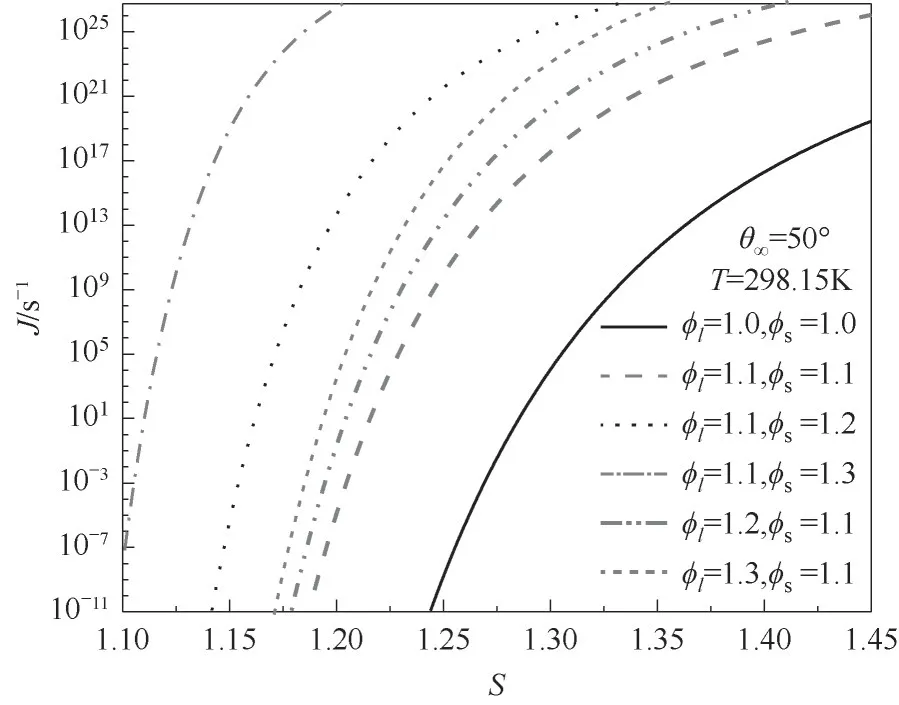
图5 不同粗糙度因子下成核速率随过饱和度的变化规律Fig.5 The nucleation rate varies with supersaturation under different roughness
由图5可知,无论是对于光滑表面的细颗粒,还是粗糙表面的细颗粒,液滴晶核的成核速率J对于水汽过饱和度S的变化极为敏感,且随着水汽过饱和度增大,成核速率都几乎呈指数型增长,如对于粒径为1μm光滑表面(φl=1.0,φs=1.0)的细颗粒,水汽过饱和度由1.30增大到1.40时,成核速率约从1.09×104s-1增大到1.99×1016s-1;同样,对于粒径为1 μm粗糙表面(φl=1.1,φs=1.1)的细颗粒,水汽过饱和度由1.30增大到1.40时,成核速率约从3.50×1017s-1增大到2.54×1024s-1。这主要是因为随着水汽过饱和度的增大,环境中的水汽分子数量增加,提高了水汽分子在细颗粒表面凝结长大的速率,同时降低了异质核化所需的成核势垒,增大了水汽在细颗粒表面发生异质核化的概率,因而增大了成核速率。
从图5还可看出,在相同的水汽过饱和度的条件下,与光滑表面的细颗粒相比,粗糙表面细颗粒的成核速率更大,且随着细颗粒粗糙度因子的增大,成核速率也相应增大,这说明颗粒的粗糙度对水汽在细颗粒表面发生异质核化的成核速率有重要的影响。与线粗糙度因子相比,颗粒的表面粗糙度因子对成核速率的促进作用更为明显,如对于粒径为1μm的细颗粒,在过饱和度S=1.30的条件下,当φl=1.1,φs=1.1时,细颗粒的成核速率约为3.50×1017s-1;当φl=1.1,φs=1.2时,细颗粒的成核速率约为2.18×1025s-1;而当φl=1.2,φs=1.1时,细颗粒的成核速率约为2.25×1020s-1。这是因为细颗粒物表面粗糙度因子的增大意味着细颗粒物的表面积增大,水汽分子与细颗粒物接触的概率增大,从而使更多的水汽分子在细颗粒表面凝结,增大了成核速率。
在线张力τ=-1.1×10-11N,颗粒粗糙度因子为φl=1.1,φs=1.1的计算条件下,对于不同粒径的细颗粒物,其成核速率随水汽过饱和度的变化规律如图6所示。
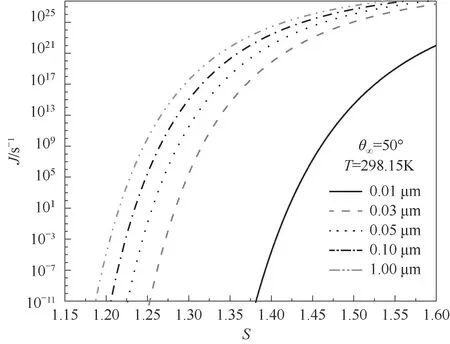
图6 不同粒径下成核速率随过饱和度的变化规律Fig.6 The nucleation rate varies with supersaturation under different particle sizes
从图6可知,在水汽过饱和度相同时,随着细颗粒物粒径的增大,其成核速率也相应增大,如在水汽过饱和度S=1.30时,细颗粒物的粒径由0.03μm增大到0.05μm,其成核速率由2.78×105s-1增大到3.22×1011s-1,增大了约106倍,随着细颗粒物粒径的增大,一方面由于颗粒的表面积与粒径的平方呈正比关系,所以细颗粒物的表面积也呈平方型增长,细颗粒物表面积的增加,使得更多的水汽分子在细颗粒物表面凝结,从而提高了成核速率;另一方面随着细颗粒物粒径的增大,水汽在细颗粒物表面异质核化的临界成核自由能减小,临界过饱和度减小,使得有更多的水汽分子在表面凝结,从而提高了成核速率。
2.4 粗糙度对临界过饱和度的影响
临界过饱和度Scr是指在单位时间内,水汽在细颗粒物表面发生核化凝结生成临界半径为r*的液滴晶核时所对应的水汽饱和度,即成核速率J=1 s-1时所对应的水汽饱和度。当水汽饱和度达到临界过饱和度时,水汽分子即以自发的方式在细颗粒表面上大量形成,出现明显的核化凝结现象。因此它是判断水汽在细颗粒表面上能否发生异质核化的重要参数。
图7所示为在温度为298.15 K、宏观接触角为50°时,在不同线粗糙度因子和表面粗糙度因子下临界过饱和度随细颗粒物粒径的变化规律。
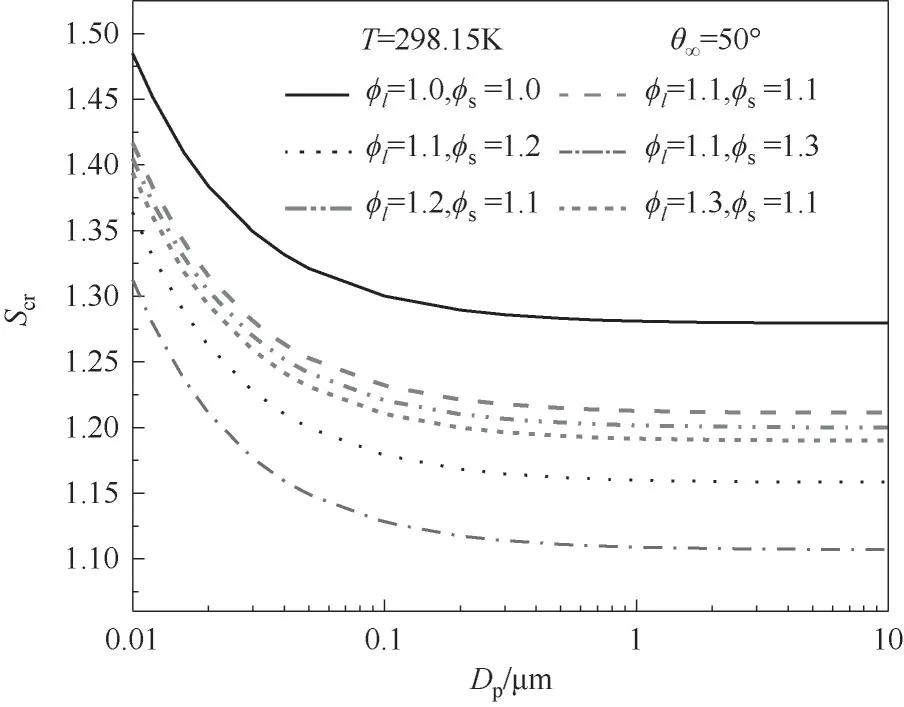
图7 不同粗糙度因子下临界过饱和度随粒径的变化规律Fig.7 The critical supersaturation with particle size under different roughness surfaces
从图7可知,无论是光滑表面还是粗糙表面的细颗粒,其粒径(Dp)对临界过饱和度(Scr)都有重要影响;对于粒径为0.01~0.1μm的细颗粒物,随着粒径增大,临界过饱和度明显减小;对于粒径大于0.1 μm的细颗粒物,随着粒径增大,临界过饱和度减小缓慢;细颗粒物粒径越大,水汽分子在其表面发生异质核化所需的临界过饱和度越小,发生异质核化的水汽饱和度要求越低,如对于光滑表面(φl=1.0,φs=1.0)且粒径大于0.1μm的细颗粒,其发生异质核化所需的临界过饱和度小于1.35。
从图7还可以看出,颗粒的粗糙度对于临界过饱和度有重要影响。如对于粒径为0.1μm的细颗粒,当φl=1.0,φs=1.0时,其临界过饱和度为1.3001;而当φl=1.1,φs=1.1时,其临界过饱和度为1.2318。这说明与光滑表面的细颗粒相比,粗糙表面的细颗粒核化所需的临界过饱和度更小,且颗粒的粗糙度因子越大,其临界过饱和度就越小,这与粗糙度对于临界成核自由能的影响规律相似。与线粗糙度因子相比,表面粗糙度因子对临界过饱和度的影响更大,如对于粒径为0.1μm的细颗粒,当φl=1.1,φs=1.2时,其临界过饱和度为1.1789;而φl=1.2,φs=1.1时,临界过饱和度为1.2206。这说明由表面粗糙度因子所影响的颗粒表面积在成核时所起到的作用更为重要,更大的颗粒表面积意味着核化所需的临界过饱和度越小,水汽在细颗粒表面的异质核化更容易发生。
由于燃煤细颗粒物的种类不完全相同,其物化特性也会有所差别,而颗粒的润湿性是影响水汽在细颗粒表面发生核化凝结的一个重要物性参数。颗粒的润湿性主要通过颗粒与液滴晶核之间的宏观接触角来反映。一般来说,宏观接触角越小,细颗粒物表面的润湿性越好,水汽在较低的过饱和度下即可在细颗粒物表面发生异质核化凝结;反之,宏观接触角越大,细颗粒物表面的润湿性越差,水汽在细颗粒物表面上发生异质核化的成核势垒越大,越不利于水汽在细颗粒物表面发生异质核化。徐俊超等[24]通过实验方法测定了不同燃煤电站细颗粒物的宏观接触角,其测量值如表1所示。
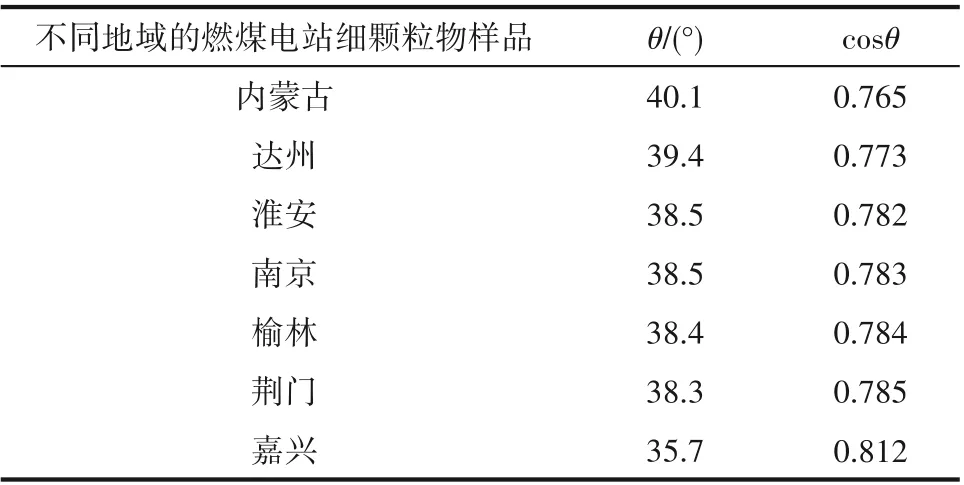
表1 不同燃煤电站细颗粒物的宏观接触角及余弦值Table 1 Macroscopic contact angle and cosine values of particles in different coal-fired power stations
从表1中可以看出,燃煤细颗粒物的宏观接触角大多在35°~41°之间,因此,选取榆林电站的燃煤飞灰颗粒物为代表,其宏观接触角为38.4°,图8所示为在温度为298.15 K,宏观接触角为38.4°时,在不同线粗糙度因子和表面粗糙度因子下临界过饱和度随细颗粒物粒径的变化规律。
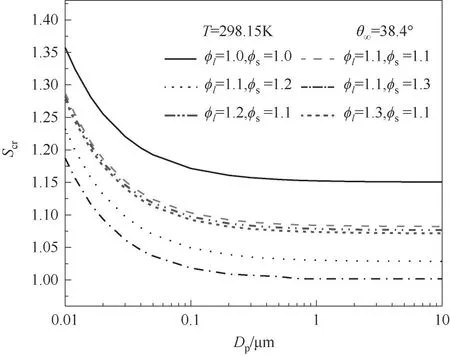
图8 38.4°时不同粗糙度因子下临界过饱和度随粒径的变化规律Fig.8 The critical supersaturation with particle size under different roughness at macroscopic contact angle 38.4°
从图8可知,对于光滑表面和粗糙表面的细颗粒,其粒径增大,临界过饱和度减小,发生异质核化所需的水汽饱和度要求降低,这与图7中宏观接触角为50°时的影响规律相类似,因此,对于燃煤电站的真实细颗粒物,本文的研究结果具有一定的参考价值。
3 结 论
(1)基于Fletcher经典核化理论并同时考虑了水汽分子表面扩散机制、线张力和颗粒表面粗糙度三种作用的理论模型预测的临界过饱和度,与已有的实验研究结果更接近,可以较好地预测核化的特性参数。
(2)随着细颗粒物的粒径增大,异质核化的临界成核自由能和临界过饱和度减小,成核速率增大。
(3)与光滑表面的细颗粒相比,粗糙表面的细颗粒与水汽间的微观接触角更小,颗粒的润湿性更好,水汽在细颗粒表面发生异质核化的可能性更大。
(4)随着细颗粒粗糙度因子增大,其成核自由能和临界过饱和度减小,成核速率增大,有利于促进发生异质核化现象。
(5)与线粗糙度因子相比,颗粒的表面粗糙度因子对水汽在细颗粒表面异质核化的影响更大。
