不同转速下微型推进器水动力特性数值研究
2021-08-31陈猛飞袁建平王彪彪司乔瑞
黄 强,陈猛飞,袁建平,王彪彪,司乔瑞
(1.中国石油化工股份有限公司 天津分公司,天津 300271;2.江苏大学 流体机械工程技术研究中心,江苏镇江 212013)
0 引言
微型推进器是水下潜航器和水下机器人等设备的动力装置,常和电机耦合在一起,通过多个推进器配合使载体按预定的轨迹运行,广泛应用于大坝闸阀水下检测、水下侦查以及水环境检测等工程领域。微型推进器工作时,电机带动叶轮旋转,液体在推进器叶轮处被加压,并经导管部件从推进器的喷口喷出,产生推力[1-4]。叶轮加压后的流体若经过导叶整流则称该类推进器为泵喷,直接喷出则称为导管螺旋桨。推进器的运行工况主要通过转速来调节,不同转速下,进入推进器的流场体会产生不同程度的不稳定流动,进而影响推进器的性能。
长期以来,国内外研究者从理论分析、试验研究和数值模拟3 个方面对推进器水动力特性进行了研究。KINNAS 等[5-6]介绍了一种以速度势为基础的导管桨推进器的设计方法,提供了详细的设计模型和相关实验数据,并分析了该推进器的水动力性能。杨福芹等[7]通过改变船舶喷水推进器的进水流道管径和转速,以“船+进水流道+喷水推进器”的流场进行了参数化仿真计算分析。邱铖铖等[8]运用数值模拟的方法研究了在不同进速系数、不同叶尖间隙和不同斜流角下,泵喷推进器激振力、压力系数和流体动力系数差异的变化规律。KAWAKITA 等[9]根据导管桨的相关试验数据,建立了非线性尾涡模型来修正线型尾涡模型的误差,并利用该模型研究了导管桨的水动力特性。吴家鸣等[10]建立了基于RNG k-ε湍流模型的导管螺旋桨水动力特性及周围流场特征、进速、诱导速度等的数值预测方法。曹玉良等[11]运用CFD 方法分析了喷速比对浸没式喷水推进器的水力性能和空化性能的影响。胡健等[12]使用多重参考系的方法对导管桨的水动力性能进行了数值研究,发现在来流为斜流的条件下,导管能够显著减小推进器工作时产生的推力脉动和扭矩脉动。
随着计算机技术的快速发展,数值模拟逐渐成为推进器研究的主要手段,但关于不同转速下的流场流动特性及其对推进器水动力性能影响的分析较少。因此,本文基于k-ε湍流模型,对微型推进器进行全流场数值模拟,分析5 种转速下推进器流场分布和水动力特性变化规律。
1 控制方程、研究对象和模型建立
1.1 控制方程
本文设定流体为不可压缩流体,则推进器周围流场的控制方程为RANS 方程[13]。
连续性方程:
式中 ui,uj——速度分量时均值,i,j=1,2,3;
ρ ——流体密度;
t ——时间;
p ——压力时均值;
gi——重力加速度分量;
μ——流体动力黏度系数。
1.2 推进器的结构及参数
本文研究的微型推进器外形结构如图1 所示,其主要水力部分为叶轮和导管,属于导管螺旋桨范畴,其前后无导叶,以4 根圆柱对导管进行支撑。水力部件的主要几何参数如下:进口直径为105.5 mm;出口直径为84.5 mm;导管长度为54 mm;轮毂比为0.2;叶轮直径为80 mm;叶轮叶片数为3 个;叶根处翼型长度为31.3 mm;叶稍处翼型长度为17.5 mm。

图1 原型推进器的组成Fig.1 Composition of prototype thruster
1.3 计算域及网格划分
根据文献[14],推进器所在的流域设置为圆柱形区域,入口到叶轮的距离为8D(D 为叶轮直径),出口到叶轮的距离为15D,圆柱的半径为5D,如图2 所示。计算域分为外流场流体域、导管流体域及叶轮流体域3 部分。

图2 计算域几何模型Fig.2 Computational domain geometric model
采用结构化网格对各流体域部件进行网格划分,并对叶根、叶稍间隙等流动复杂区域进行加密处理,同时划分边界层,使所有计算区域壁面网格y+小于80,网格划分结果如图3 所示。本文共划分5 套网格进行网格无关性分析[15-16]。

图3 各流体域部件结构化网格划分Fig.3 Structured meshing of components in each fluid domain
图4 示出了在转速为4 000 r/min,进口流速为0.1 m/s 的条件下网格数与推力的变化关系。由图可知,推进器的推力随着网格数的增加而减小,当网格数达到480 万左右时,推力的大小趋于稳定,即随着网格数的继续增加推力几乎不变。因此,为了同时兼顾计算效率与计算精度,本文采用总数为480 万的网格进行数值模拟,其中,叶轮的网格数为152.33 万,导管的网格数为81.56 万,外流场的网格数为247.47 万,各部分网格质量都在0.46 以上。
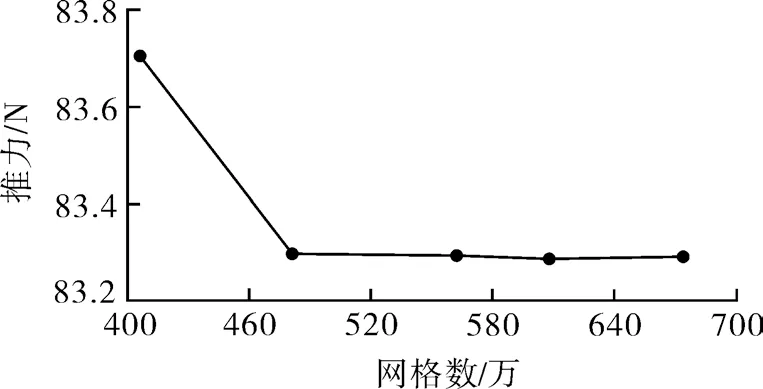
图4 4 000 r/min 转速下的网格无关性Fig.4 Grid independence at 4 000 r/min speed
1.4 计算边界条件的设定
采用CFX 软件对计算域进行数值模拟时,入口边界设定为速度入口;出口边界设定为自由出流,其压力为1.01×105Pa(1 atm);圆筒表面设为无滑移壁面;旋转水域绕轴以转速n 旋转;使用有限体积法离散控制方程和湍流模式,湍流模型选用k-ε模型;采用稳态多参考系(MRF)处理推进器所处的旋转域和其他区域的相对运动[17-19];以RMS 残差为10-5作为收敛依据进行迭代计算。
2 模拟计算结果及分析
为了分析不同载荷下转速对推进器水动力特性的影响,设定入口来流速度为0.1 m/s 并保持不变,模拟转速为2 000,2 500,3 000,3 500,4 000 r/min的5 种运行工况,得到不同转速下推进器的水动力性能。数据处理中推力F 和功率P 分别按下式计算:

2.1 推进器的性能分析
分别将转速n、推力F 和功率P 的数据进行对数化处理来减小数据拟合时的误差,并利用最小二乘法原理拟合出lgn 与lgF,lgn 与lgP 之间的直线关系,结果如图5 所示。
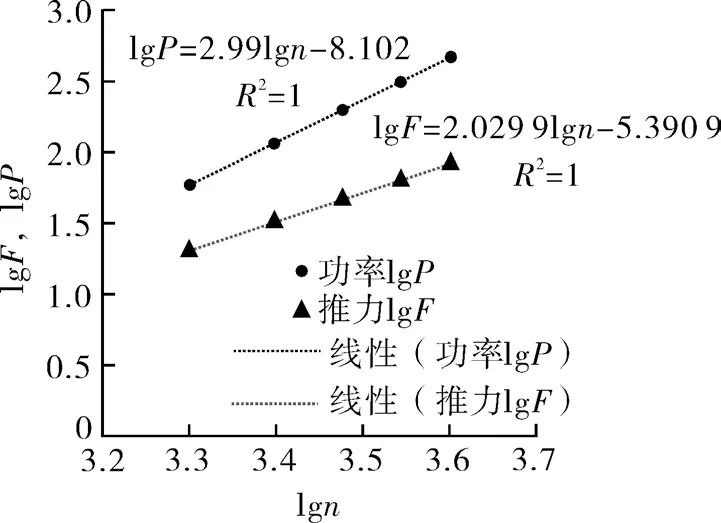
图5 各转速lgn 下的推力lgF 和功率lgPFig.5 Thrust lgF and power lgP at each speed lgn
lgn 与lgF 的关系式为lgF=2.029 9lgn-5.390 9,其中R2=1,表明回归效果非常显著,可认为推力F与转速n 的二次方成正比;lgn 与lgP 的关系式为lgP=2.991lgn-8.102,其中R2=1,表明回归效果非常显著,可认为功率P 与转速n 的三次方成正比,与文献[20]里的研究结论一致。
图6,7 示出了不同转速下微型推进器叶片表面的静压分布,通过观察、对比发现,微型推进器的叶轮推力面大部分为正压分布,吸力面大部分为负压分布;当转速从2 000,2 500,3 000,3 500到4 000 r/min 变化时,推力面正压幅值和吸力面负压幅值均逐渐变大。叶轮吸力面负压主要分布在导边和叶梢部分,表明在该微型推进器运行过程中,空泡最有可能在吸力面的导边附近初生。另外,由图6,7 可以看出,在导边处压力面与吸力面的压力差最大,即导边处所受的应力最大;并且随着转速的增大,导边处所受应力在不断增大,因此,导边处可能需要进行应力强度校核。
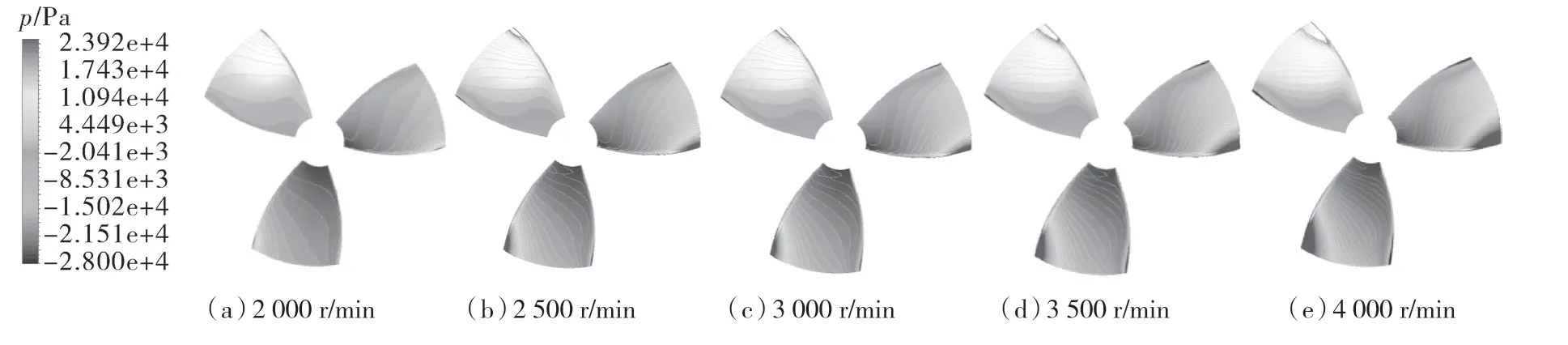
图6 各转速下推进器压力面压力云图Fig.6 Pressure nephogram of the pressure surface of the thruster at each speed

图7 各转速下推进器吸力面压力云图Fig.7 Pressure nephogram of the suction surface of the thruster at each speed
图8,9 示出了微型推进器叶片表面湍动能分布,其湍动能的大小和空间分布的不均匀性从侧面说明了黏性耗散损失、流动分离以及脉动扩散程度的大小[21]。从图中可以看出,叶片压力面与吸力面的湍动能均沿叶根至叶稍递增;在靠近叶稍区域,湍动能从导边到随边呈现递减趋势,这主要是因为在导边处,流体分离成两股,分别流过叶轮的压力面和吸力面,由于叶片对流体做功,使其流动趋于稳定,流动损失逐渐减小。从整体上看,随着转速的增大,流体进入推进器的流量和流速增加,产生变化剧烈的湍流流动,导致叶片表面的湍动能不断增大,流体扰动增强。
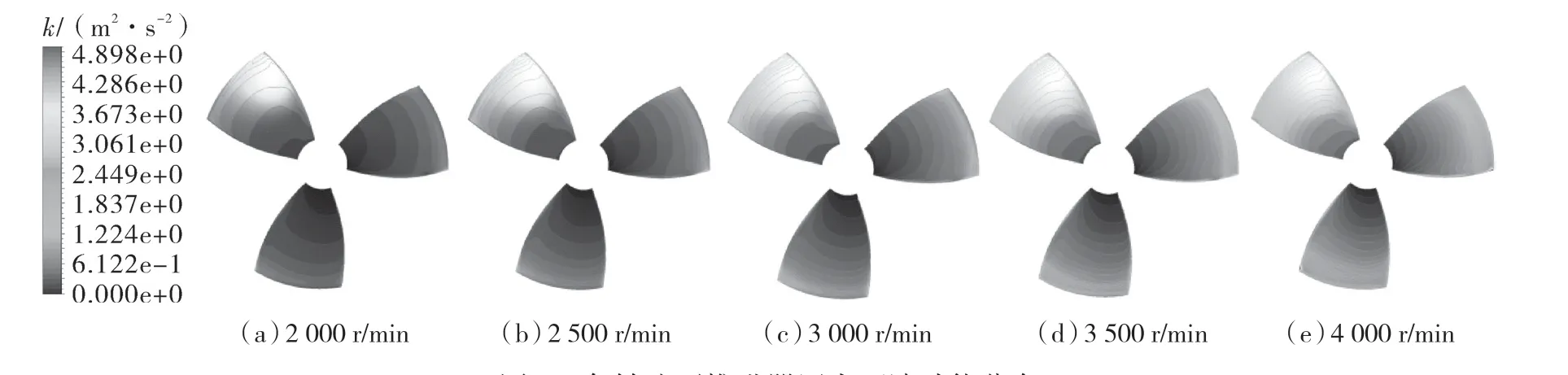
图8 各转速下推进器压力面湍动能分布Fig.8 Turbulent kinetic energy distribution on the pressure surface of the thruster at each speed
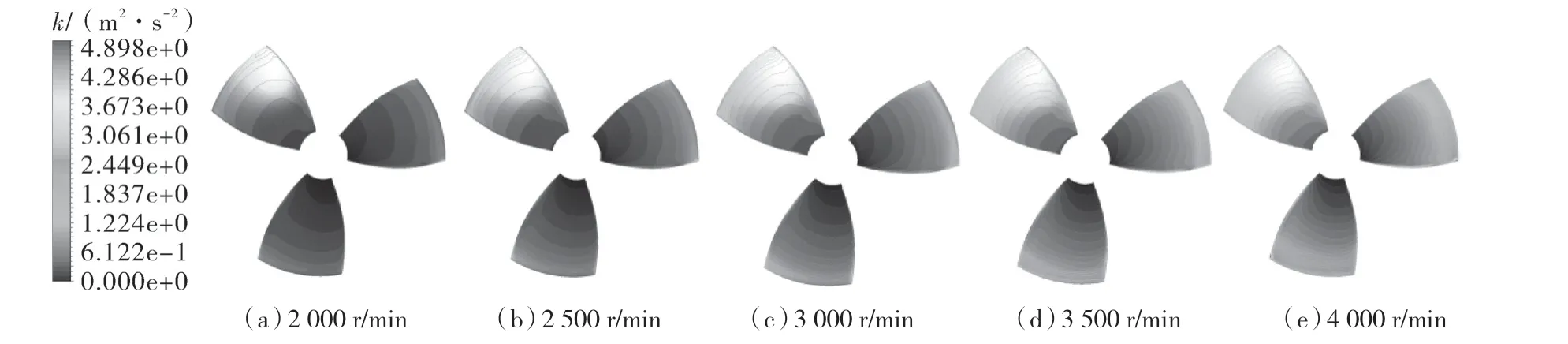
图9 各转速下推进器吸力面湍动能分布Fig.9 Turbulent kinetic energy distribution on the suction surface of the thruster at each speed
2.2 微型推进器工作流场分析
图10 示出了微型推进器在5 种转速下轴截面上的流线,从图可以清晰地看出,微型推进器在水下的工作过程:流体由导管进入推进器,经过叶轮的加压做功,速度和压力升高,最后从尾部喷口喷出,与推进器外流场的低速低压流体相互混合作用,在尾流区的两侧形成一对旋转方向相反的非对称旋涡。从图10 中可以看出,随着转速的增大,推进器喷口水流的速度幅值逐渐增加,尾流区所产生的旋涡强度和范围也在逐渐增大,这说明喷口水流的动量和流量都在随着转速的增大而增加,使推进器所产生的推力不断增大。

图10 各转速下沿轴向切面速度流线分布Fig.10 Velocity streamline distribution along axial section at each speed
图11~14 示出了距离叶轮分别为1D,2D,3D,4D(导管出口盘面)位置截面的速度分布云图。从图11 中可以看出速度核心区主要存在于导管出口盘面部分,呈现出关于中心轴对称的三角星型分布;在中心处存在一块圆形的低速区,表明在推进器运行过程中在该处易产生旋涡或空泡。通过对比图11~14 可以发现,随着与叶轮距离的增大,速度核心区的范围在不断增大,并沿顺时针方向旋转,同时其速度峰值不断减小,说明水流从喷口喷出后不断与周围的低速水流混合,水流速度逐渐趋于均匀。

图11 各转速下离喷口1D 截面处速度云图Fig.11 Velocity nephogram at 1D section away from the nozzle at each speed
此外,随着转速的增大其速度核心区的范围和速度峰值不断增大,说明随着推进器转速的增大,其出口水流的动能不断增大。

图12 各转速下离喷口2D 截面处速度云图Fig.12 Velocity nephogram at 2D section away from the nozzle at each speed
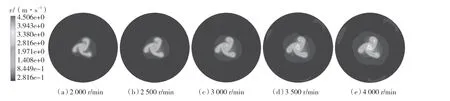
图13 各转速下离喷口3D 截面处速度云图Fig.13 Velocity nephogram at 3D section away from the nozzle at each speed

图14 各转速下离喷口4D 截面处速度云图Fig.14 Velocity nephogram at 4D section away from the nozzle at each speed
3 结论
(1)随着推进器转速的增大,其推力和功率都在不断增加,并且推力与转速的二次方成正比,功率与转速的三次方成正比。
(2)推进器叶轮导边所受应力和流动损失最大;随着转速增大,叶轮所受应力和流体湍动能不断增大。
(3)推进器的尾流区存在一对旋转方向相反的非对称旋涡,其强度随转速增大而增加;喷口处水流受叶轮的影响较大,由于其周向速度较大,可在叶轮后方增设导叶来吸收喷口水流的旋转动能,进而提高推进器的推进效率。
