基于PCA_Adaboost模型的上市公司投资策略研究

叶殷如

（深圳市前海汇富联合基金管理有限公司，广东 深圳 518000）

量化投资，即根据金融逻辑或统计规律等建立数学模型，并通过计算机进行策略的实现，近年来在国内金融市场上的地位日渐提高，在A 股市场中越来越多的机构与个人投资者开始使用量化方式指导投资决策。A 股市场中，量化策略按频率分类主要分为高频策略与中低频策略，高频策略数据最小时间单位为1tick（3 秒），中低频策略数据最小时间单位为天。中低频策略主要由交易型策略和基本面策略组成，而基本面量化最常见的一种模型大类为多因子模型，例如回归模型、机器学习模型等。

对于A 股中低频策略，多因子模型中的中低频因子多为财务因子或财务衍生因子，由于因子众多，因子间相似程度较高，计算机处理相关因子数据时有过多噪声和不必要的运算，影响策略运行效率与质量，因此有必要对因子进行降维处理。在现行市场上中低频因子逐渐失效的现实背景下，机器学习方法可以通过对大量历史数据进行统计、回测、总结、计算和预测，达到提高胜率的目的。本文提出PCA_Adaboost 模型，即首先通过PCA 算法对多因子进行降维，得到的新因子作为Adaboost 的弱分类器，最终迭代学习出强分类器。

1 模型介绍

1.1 Adaboost 模型

Adaboost 是一种常用的分类模型。Adaboost 算法是boosting 算法的一种改进［1］，对多个弱分类器通过迭代进行权重的调整，最终合并成强分类器，提高分类性能，降低误差。具体过程如下：

（1）假设测试数据为｛（x1，y1），（x2，y2），…，（xn，yn）｝，其中y 为样本标签，y∈｛-1，1｝；

（3）迭代T 次，得到强分类器

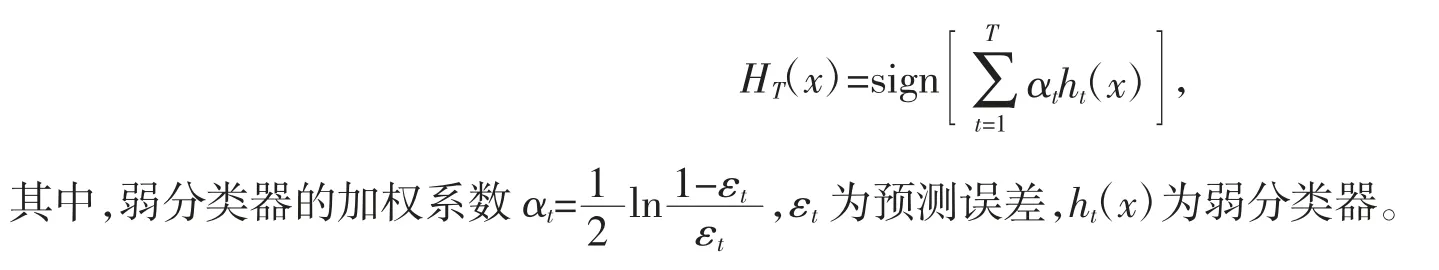
从模拟公式可以看出，弱分类器数量越多，迭代次数T 越大，计算冗余越多，模型运行耗时越长，计算精度越低。因此可结合PCA 方法对Adaboost 算法进行降维处理。

1.2 PCA 模型

传统的Adaboost 模型首先将每个特征值对应一个简单分类器，再进行弱分类器的计算［2］，但当特征值数量多且可能存在一定相关性的情况下，容易出现计算冗余，从而降低计算速度与计算精度，因此，可通过降维的手段，使用涵盖信息量大且相关性低的新特征值进行替换。

PCA 算法是一种用于降维的无监督学习方法，其原理为基于变量的协方差矩阵进行线性变换，基础为K-L（Karhunen-Loeve）变换理论［3］。该方法根据多个因子面板数据，构成因子的协方差矩阵并进行变换计算，以达到将多因子转换成相关性低的少数几个主因子。具体过程如下：

假设有m 个上市公司，n 个因子，对数据进行去极值和标准化处理，记该矩阵为

求相关性矩阵R，R=（rij）n×n，则

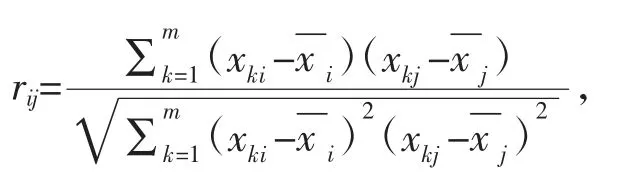
其中，rij=rji，rii=1。

求R 的特征方程det（R-λE）=0 的特征根λ1≥λ2≥λ3≥…≥λn＞0。

确定主成分个数p，根据实际问题确定

其中，a 为信息量比例置信度。

计算p 个单位对应的特征向量，计算公式为

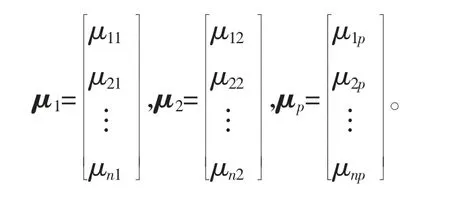
所求主成分为

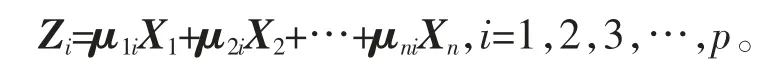
2 实证分析

2.1 数据准备

本文基础股票池为中证500 内所有上市公司，对比标的为中证500 指数。测试时间段为2018 年7月1 日至2019 年12 月31 日。使用因子库中涵盖估值、财务质量、成长性、量价指标等全部134 个因子，采用PCA 算法对其进行数据优化处理。

此次试验中，换仓周期取为21 天，每期学习样本窗口取为半年。为了降低数据噪声对模型精度造成的影响，学习样本仅取当天对应的未来21 天收益最高与最低的股票，即将未来21 天的超额收益按降序排列，取最高10%的股票标签值记为1，最低的10%记为-1。因此，Xm×n矩阵由该样本窗口内每一天对应的因子数据构成，Ym×1矩阵由样本窗口内每一天对应的未来21 天收益所对应的标签值构成。

检验（预测）样本数据为第di天的因子数据，利用学习样本窗口期的因子数据进行学习并得预测矩阵Y，根据预测的y 值选择第di+1天买卖的股票，持有21 天后统计超额收益等相关指标，记录后进行下一轮计算。

2.2 PCA 参数选择

对全部134 个因子进行主成分分析，以确定主成分个数，如图1 所示，信息量比例为各主成分的方差值占总方差的比例之和，可观察到随着主成分数量的增加，信息量比例同步增加，但增加的幅度逐渐减缓，为保证信息量比例在80%以上，此处选择主成分的个数为30 个。

图1 总方差-主成分数量统计图

2.3 Adaboost 模型参数优化

Adaboost 中有参数叶子节点最小深度、决策树最深层数等参数需要设置，以使学习效果最好并降低过度拟合的风险，其中MD 为决策树最大深度，MSS 为子树再划分最小样本数，MSL 为叶子节点最小深度，NE 为弱学习器最大个数，LR 为权重调整系数为0.8。对上述参数进行优化组合，以使超额夏普率最高。回测结果中，AlphaSharp 为超额夏普比率，AlphaRtn 为超额收益，AlphaDrawdown 为超额收益在回测时间段中的最大回撤。

如表1 所示，所有参数组合结果与标的指数相比皆有明显的正收益与正的超额夏普比率。当MD=3，MSS=30，MSL=5，NE=250 时，策略组合的超额夏普比率最高，超额收益最高，最大回撤较低。对于其他参数组合的结果，策略皆表现为具有超额收益与正的夏普率，模型有一定鲁棒性。

表1 组合优化结果

如图2 所示，组合策略对于中证500 指数有明显的正阿尔法收益，阿尔法策略回撤相比纯多头策略或指数明显减小，且收益稳定。在急跌的市场环境中仍具有正的收益，抗风险能力较强。

图2 PCA-Adabbost 与中证500 收益图

图3 为每次换仓的胜率分布图，按次统计平均胜率为51.5%，绝大部分次数胜率超过50。第2 类错误比例高于第1 类错误，且在大盘下跌时胜率会有所降低，存在改进空间。

图3 胜率统计图

如图4 所示，对不进行主成分分析，直接将所有因子输入Adaboost 模型所得策略与PCA_Adaboost策略比较，纯Adaboost 策略累计收益较小且回撤较大，总体效果不如后者，PCA_Adaboost 策略对纯Adaboost 策略有明显提升。

图4 PCA-Adabbost 与Adaboost 收益图

如图5 所示，预测标签值为1 的多组合比预测标签值为-1 的空组合收益更高。若交易规则允许做空或通过融券做空，做多多组合，做空空组合，测试结果在回测时间段内收益为10.55%，夏普比率为2.88，组合最大回撤-2.6%。多空组合策略收益稳定，效果显著。

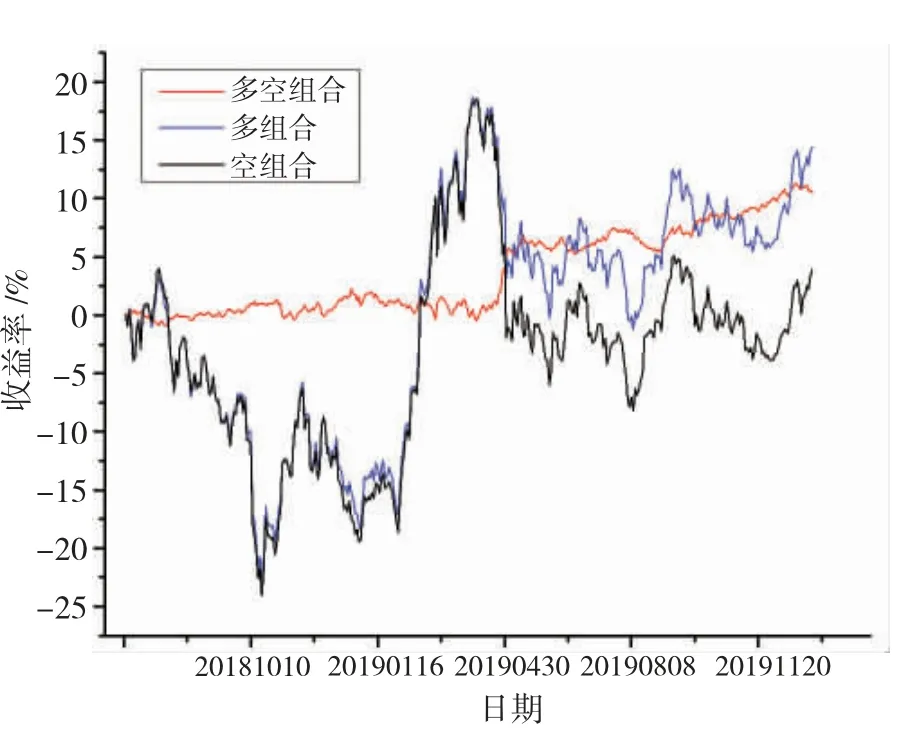
图5 多空组合效果图

3 结论与展望

以上实验可观察出PCA_Adaboost 策略对标的指数中证500 有明显的超额收益，当决策树最大深度为3，子树再划分最小样本数为30，叶子节点最小深度为5，弱学习器最大个数为250 时，策略换仓平均胜率超过50%，且收益最高，回撤较小，组合阿尔法的夏普率最高，对比纯Adaboost 的策略效果更佳，优化效果明显。做多预测标签值为1，做空预测标签值为-1 的多空策略亦保持高收益率。综上所述，PCA_Adaboost 投资策略具有稳定的超额收益，小的波动，在A 股上市公司投资中有一定的应用前景。另一方面，此策略仍有改进空间。通过对比观察图2 与图3，急跌行情中胜率下降，但Alpha 收益却稳步上升，代表个股权重或行业偏离对选股策略结果仍有所影响，而本次PCA_Adaboost 并未加以考虑。后续研究中，可结合权重修正、行业中性化等方向对模型进行优化。