线性方程的解A-、A+的应用——

余新宏，胡 勇，魏明锐

（安徽农业大学 经济技术学院，安徽 合肥 230011）

线性方程组本身可能是相容的，即它是有解，也可能是不相容的。对于相容方程组，需要求出它的全部解；对于不相容方程组，需要确定出它的所谓最小二乘解。邓勇［1］研究了相容线性方程组通解中的未知数被唯一确定的充分必要条件，讨论了相容线性方程组中有唯一确定解的未知数的数量问题，进一步得到相应的求解公式。对于不相容线性方程组的解，施妮沙［2］用微积分方法给出不相容方程组的最小二乘解以及相容线性方程组极小范数解。线性方程组Ax=b 的解与A-、A+也有着密切的关系，韩海清［3］对矩阵的广义逆性质和求解方法进行了研究，并利用广义逆矩阵求解线性方程组的通解及最小二乘解，本文将在此基础上，进一步就这两种情况作一些简要的讨论。

1 相容方程Ax=b 的全部解

线性齐次方程

易知它的同解为

其中，μ是任意向量。事实上，

于是x=（I-A-A）μ是齐次方程Ax=0 的解。反之，如果x 是解，则满足齐次方程Ax=0，故x=A-Ax+（I-A-A）x=（I-A-A）x，也就是说，它必为（I-A-A）μ的形式，因此得证。

线性非齐次方程

当它为相容方程时，它的同解是

其中，μ是任意向量，A-是A 的某个固定的负号逆。

事实上，只需证明A-b 为非齐次方程的一个特解就可以了。由于Ax=b 是相容的，因此必有解，于是存在C，使得b=AC，因此

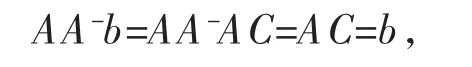
这就说明了A-b 的确是一个特解。如果用加号逆求解，则有类似的结果。总之，当Ax=b 为相容时，它的同解为

或者

其中，μ 是任意向量。由此可得：

（i）相容方程Ax=b 有唯一解↔I-A-A=0，如果A 有逆，则此解为A-1b；

（ii）齐次方程Ax=0 有非零解↔I-A-A≠0，即A-1不存在；

（iii）相容方程Ax=b，它的解中使xTx=min者为

证明事实上，Ax=b 的同解为

于是

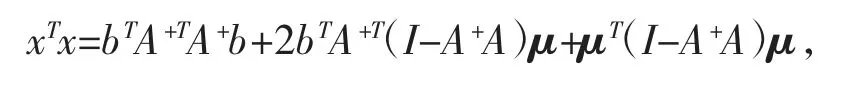
然后

因此

由投影阵知识可知，μT（I-A+A）μ≥0，于是xTx 达到最小↔μT（I-A+A）μ=0，即

2 Ax=b 为不相容的全部最小二乘方解

当Ax=b 为不相容时，使

的x 称为Ax=b 的最小二乘方解（LS 解）。LS 解总是存在的，并且其全部LS 解是

或者

其中，μ 是任意向量。

证明已知

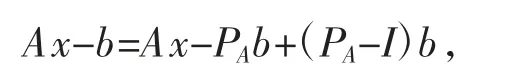
其中，PA=A（ATA）-AT。因此

由于

因为

因此

即

而Ax=PAb 是相容的，它的全部解为

其中，μ是任意向量。

注意到A-PAb=A-A（ATA）-ATb，当“-”号用“+”代替，有

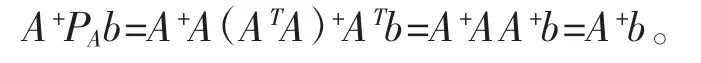
因此用A+表示时，Ax=b 的全部LS 解为

其中，μ是任意向量。且x=A+b 是LS 解中xTx=min的唯一解。