基于PNN的GIS局部放电模式识别方法

李君科，李明江，李德光

（1.黔南民族师范学院计算机与信息学院，贵州都匀 558000；2.洛阳师范学院信息技术学院，河南洛阳 471934）

气体绝缘开关设备（gas insulated switchgear，GIS）因其安全运行可靠性高、低成本、低污染运行等特点，在电力系统中得到了广泛应用[1-2]。但GIS 设备的长时间运行以及制造和安装时存在的疏漏会导致内部绝缘缺陷，引起设备的局部放电（partial discharge，PD）行为[3]。对GIS 设备内部各种绝缘缺陷的PD 信号监测并进行分析和识别，能够为评估设备运行状态和制定可靠的检修方案提供合理依据[4-5]。

目前在GIS的PD 模式识别的研究中，主要是从特高频（ultrahigh frequency，UHF）测量[6]信号中提取出类别特征集以便于分类，常用的特征量提取方法有分形特征法[7-8]、统计特征法[9-10]和矩阵特征法[11-12]等。但是，特征提取所得到的高维数据不仅增加分类器的计算量，更会引起识别率的下降。目前常用的降维方法是主成分分析法（principal components analysis，PCA）[13-14]，但是该方法基于求得样本协方差矩阵的特征贡献率，没有体现样本间的类别信息。属于监督降维的线性判别分析法（linear discriminant analysis，LDA）能够使样本空间具有明显的类别信息，提高模式识别的正确率，在各领域得到了很好的应用[15-16]。

国内外学者对GIS 的PD 模式识别进行了大量研究，其中，BP 神经网络（back propagation neural networks，BPNN）[13，17]和支持向量机（support vector machine，SVM）的应用比较广泛[7，14]。但BP网络在训练时存在过拟合、容易陷入局部极值以及收敛速度慢等问题。SVM是基于二次规划求解支撑向量，该方法随着样本增加，矩阵阶数上升，且相应的运算量和运算时间也急剧攀升。概率神经网络（probabilistic neural network，PNN）可以从海量样本中学习出类别特征信息，与其他方法相比，该方法具有收敛速度快且分类能力强等特点，在模式分类领域得到了广泛应用[12]。由于PNN对训练样本的类别信息的要求比较高，所以本文采用LDA数据分析方法，且引入遗传算法对平滑因子进行优化来提高网络的收敛速度和识别精度。

本文针对GIS 的PD 模式识别开展如下研究工作：利用GIS 局部放电高压实验平台模拟了5类典型的GIS 设备缺陷模型，采用UHF 获取局部放电的原始信号参量；采用统计特征法提取出18个统计参量并进行LDA 分析，对统计参量进行降维处理得到新的特征参量；用优化平滑因子后的概率神经网络作为PD 类型识别器对低维样本进行模式识别。

1 线性判别分析

Ronald Fisher 于1936 年提出的LDA 分析法是提取特征的有效方法。采用Fisher准则函数对多类样本数据进行线性判别分析，其目标是通过计算高维特征空间的类内离散度矩阵和类间离散度矩阵，提取出具有类别可分性的低维特征，即新样本有最大的类间距离和最小的类内距离。

式中：Sb，Sw分别为类间离散度矩阵和类内离散度矩阵；w为待求的最优投影集；ml为各个类内样本均值；m为样本空间均值。

构造拉格朗日乘子，将式（1）表示为

2 PNN识别模型及优化

2.1 概率神经网络

概率神经网络是在径向基神经网络的基础上发展起来的，融合了Parzen 窗概率密度函数估计和Bayes 分类准则，可以实现任意的非线性逼近，收敛于贝叶斯分类最优解。基本思想为：设有d维输入特征样本x=[x1，x2，x3，…，xd]，对应于C个类别w1，w2，…，wC之一。P（wi）和P（x|wi）分别为类wi的先验概率和类条件概率密度函数。贝叶斯决策通过最小化风险进行决策，决策规则为

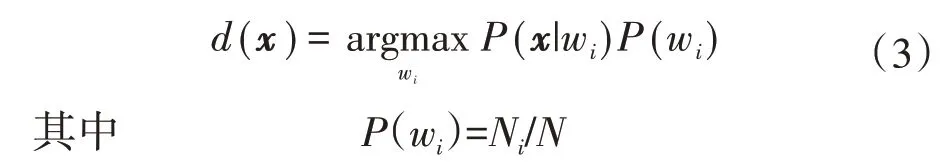
式中：d（x）为决策；P（wi）为类wi的先验概率；Ni为类别i的训练样本数；N为训练样本总数。

类条件概率密度函数P（x|wi）采用Parzen 窗非参概率密度函数方法进行估计，且将多元高斯核函数作为窗函数，即P（x|wi）的Parzen 窗估计表示为

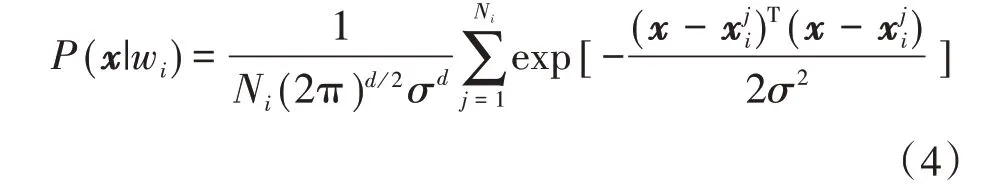
式中：Ni为i类的训练样本数；xij为该神经元的权向量（同时也是第i类中的第j个训练样本）；σ为平滑因子，决定了以样本点为中心的曲线宽度。

PNN 模型由输入层、模式层、求和层和输出层组成，结构如图1所示。

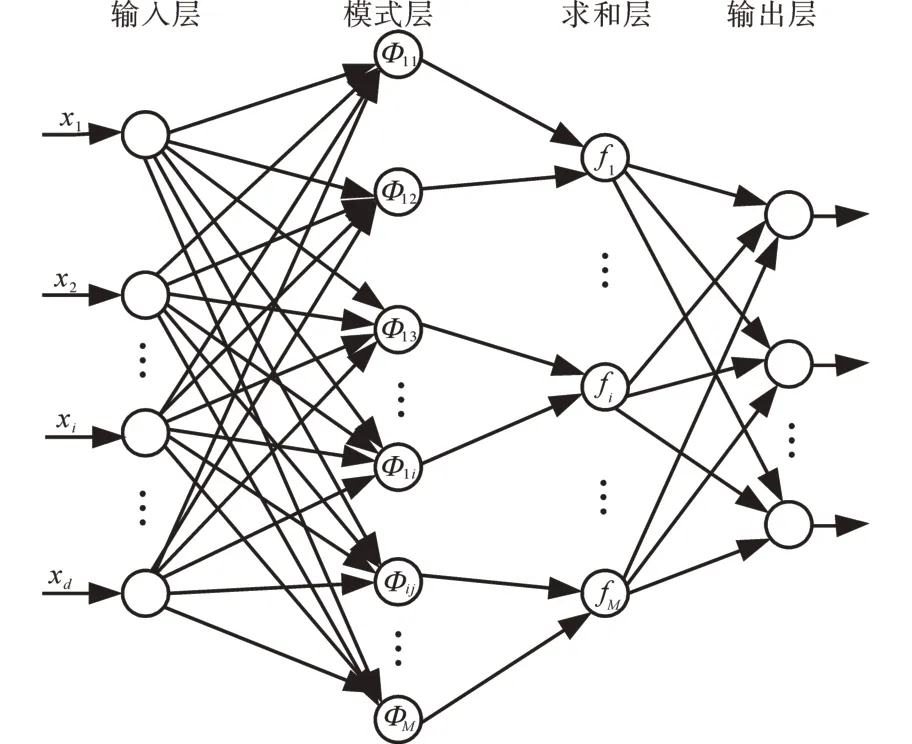
图1 PNN网络结构图Fig.1 PNN network structure diagram

1）输入层神经元个数与特征样本x的维数相等，该层接收特征空间样本并传递给网络模式层。

3）求和层神经元个数与样本类别数C相同，该层神经元与仅属于同一类的模式层神经元连接，将模式层中所有同类神经元的输出累计后取均值：

式中：Ni为训练样本类别i的数量。

4）输出层有C个神经元（对应每个模式类），该层接受求和层输出的类别条件概率密度函数，采用贝叶斯分类准则，每个神经元的输出为

对于未知类别的特征样本x，有r，s（r，s∈{1，2，3，…，C}，且r≠s），若存在Or＞Os，则判定特征样本属于r类。

由概率密度函数可知，平滑因子σ的变化会影响PNN 网络的性能。取值过小，密度估计会出现过拟合，容易受到噪声干扰；取值过大，函数逼近平滑，会增加参与计算的模式层神经元，两者皆会影响分类器的识别效果。

2.2 优化概率神经网络

目前常采用经验法确定平滑因子，但该方法不能完全表述特征样本的概率特性。遗传算法可以无需先验知识进行全局寻优，在模式识别、函数优化、控制和故障诊断等方面得到了广泛的应用[18-19]。本文选取遗传算法对PNN分类器的平滑因子进行优化，找到适合对特征样本识别的平滑因子。

采用样本特征分布信息设计初始种群来代替传统的随机分布初始种群。Parzen 概率的估计值主要是取决于临近点距离影响，当待测样本与模式样本的距离分别为1σ，2σ，3σ时，产生的相应高斯值相差悬殊，能够直接影响概率估计值。因此σ值的选取要有一定的范围，可采用下式表示：

式中：pˉav[k]为同类样本最小距离平均值；g为比例系数，选取为0.9～1.8。

遗传算法的适应度函数采用误差函数计算个体的适应度，如下式所示：

式中：E为误差值；d（xj）为期望输出；o（xj）为网络的实际输出。

综上，基于遗传算法优化的概率神经网络步骤如下：

1）计算特征空间的同类样本的最小距离平均值集，并利用比例系数在区间内形成初始种群{σ′1，σ′2，σ′3，…，σ′M}，M为种群规模；

2）进行种群二进制编码；

3）执行遗传算法的选择、交叉、变异操作，并解码；

4）评价适应度函数，得到理想平滑因子则进行步骤5），否则转入2）继续执行；

5）优化后平滑因子确定PNN 网络分类器模型。

3 局部放电实验与特征提取

3.1 实验

基于GIS局部放电高压实验平台进行模拟局步放电缺陷类型。实验平台示意图如图2 所示，试验变压器的额定电压为150 kV，额定容量为15 kV·A，隔离开关动作速度3 s 左右。瓷套用于电气设备引线的绝缘支撑。试验腔内设置缺陷类型模型，腔体内含有少量空气并充以SF6 气体至0.4 MPa。仿真平台采用UHF 检测法，检测频段为300～3 000 MHz，用以避开电晕放电等干扰。实验电路接线示意图如图3所示。

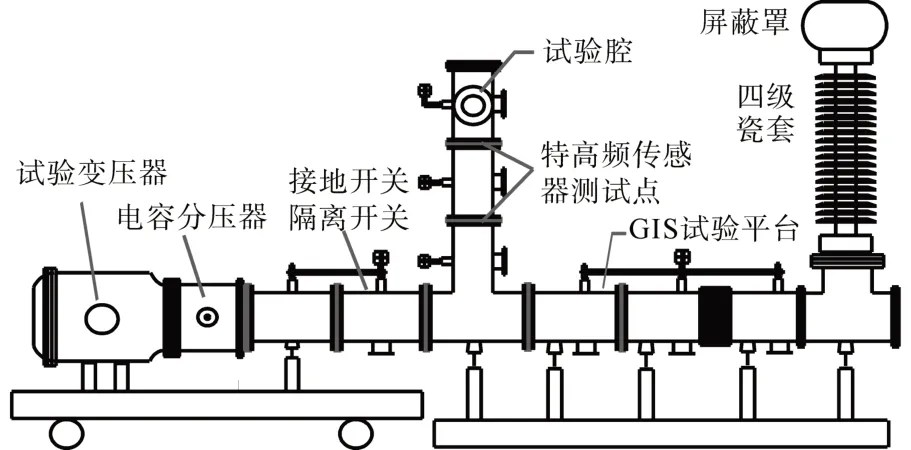
图2 实验仿真平台示意图Fig.2 Schematic diagram of experimental simulation platform

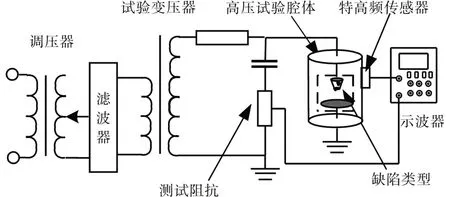
图3 实验接线示意图Fig.3 Schematic diagram of experimental wiring

针对GIS 设备在实际运行中的典型绝缘缺陷类型，设计了如尖端导体放电（T）、分散型颗粒放电（D）、集群型颗粒放电（C）、绝缘子内部放电（I）、悬浮放电（S）等5 种典型的PD 模型，如图4 所示。

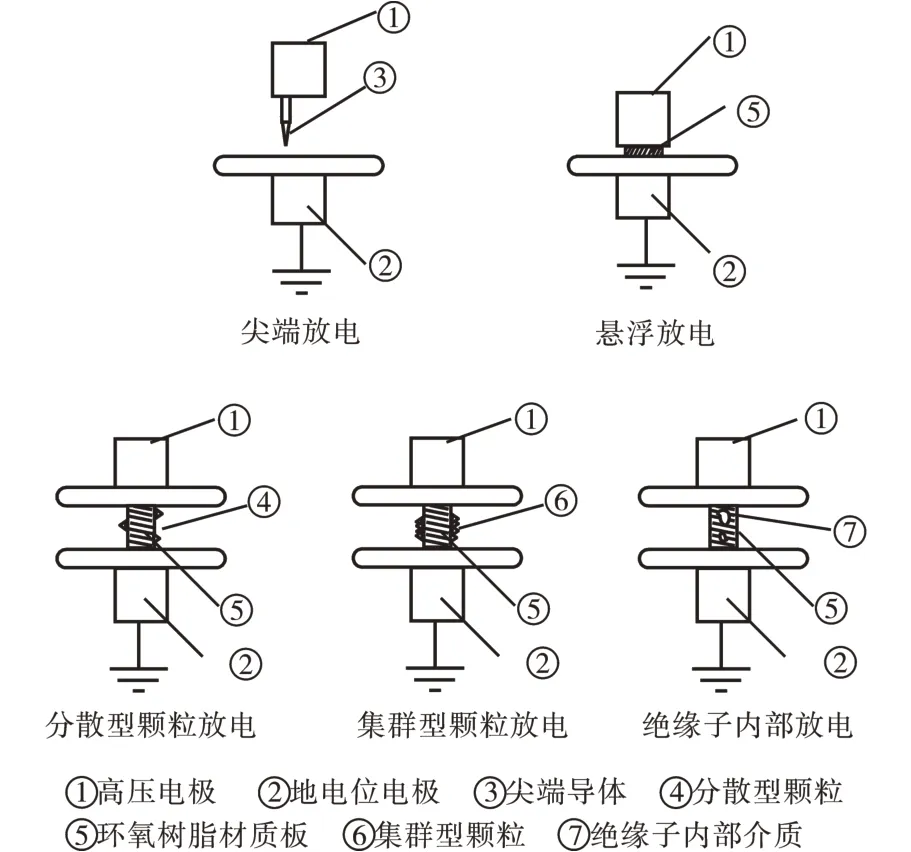
图4 典型的局部放电模型Fig.4 Typical partial discharge model

模型规格：尖端放电，选取长度l=15 mm、针尖直径d=0.5 mm 的铜质尖端导体，距离电极7 mm；悬浮电位放电，接地电极上放置厚5 mm 的环氧树脂材质板，环氧树脂板上面放置直径10 mm、高10 mm 的铜质导体；分散性颗粒群放电，选取若干直径d=0.4 mm、高h=10 mm 的铜质三角锥体，分散于GIS母线导体的绝缘子上；绝缘子表面金属颗粒群放电，选取若干直径d=0.4 mm、长高h=10 mm 铜丝，分堆放置于GIS 母线导体的绝缘子上；绝缘子内部缺陷放电，将绝缘子替换成内部有介质缺陷的绝缘材质。

3.2 超高频特征参量

3.2.1 信号采集概述特征参量提取

利用3.1 节实验平台进行局部放电实验，将上述放电模型置于试验腔内，接高、低压电极进行实验，通过UHF 检测各类缺陷的信号。每种缺陷类型采集3 000 个工频周期内的局部放电波形。将50 个周期的工频数据存为1 个样本，即每类信号含有60个样本。不同缺陷模型的PD 放电次数m，放电相位φ，放电电荷量q等统计参数有明显的差异，各缺陷类型的UHF 二维图谱如图5～图9所示。

由图5～图9 可知，T 类放电缺陷在负半周有较高的放电量，D 类缺陷在正负半周的峰值处的放电次数比较多且正半周的峰值处存在离散样本，C 类缺陷放电主要发生在正负半周的峰值之前且相应的放电量比较多，I 类缺陷在正负半周存在较少的放电量，S 类缺陷的放电分布比较分散且放电量表现比较平稳。

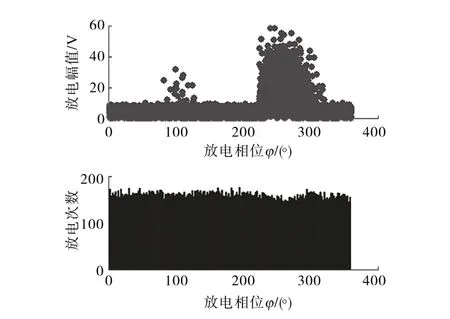
图5 尖端导体放电相位分布图谱Fig.5 Discharge phase distribution of tip conductor defect type

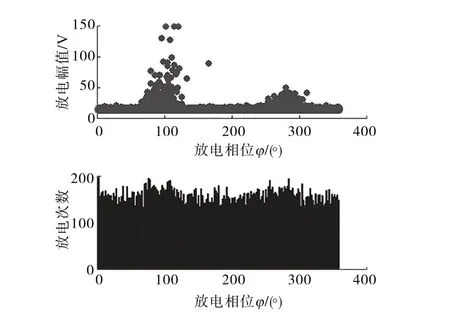
图6 分散型颗粒放电相位分布图谱Fig.6 Discharge phase distribution of dispersed particles defect type

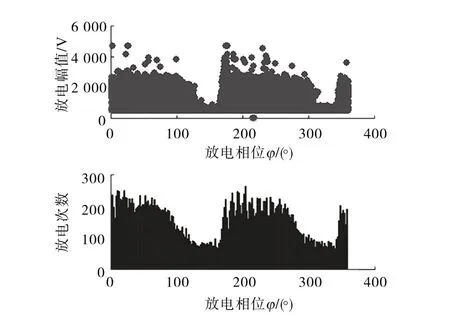
图7 集群型颗粒放电相位分布图谱Fig.7 Discharge phase distribution of clustered particles defect type

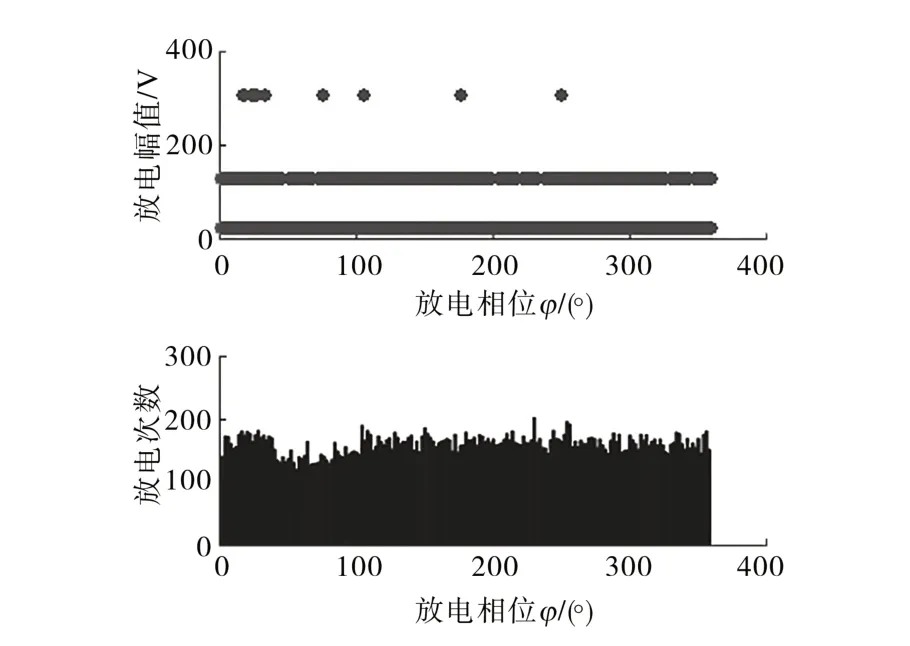
图8 悬浮放电相位分布图谱Fig.8 Discharge phase distribution of suspension defect type

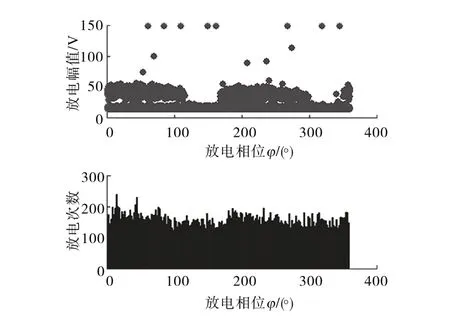
图9 绝缘内部放电相位分布图谱Fig.9 Discharge phase distribution of insulation internal defect type

依据各类缺陷的二维图谱，分别提取能够描述局部放电特性的统计算子，包含偏斜度SK，陡峭度Ku，放电量因数Q，互相关系数CC，峰值不对称度P等共18个统计参量，如表1所示。

表1 统计算子表Tab.1 Table of statistical parameters

3.2.2 统计参量的线性判别分析

以偏斜度的6 个参量为例进行LDA 数据分析，求解Fisher 准则函数矩阵的特征值及其主导向量。对求得特征值的贡献率和累计贡献率（如表2所示）进行分析，选择较大特征值的特征向量作为主要向量用以确定转换矩阵。

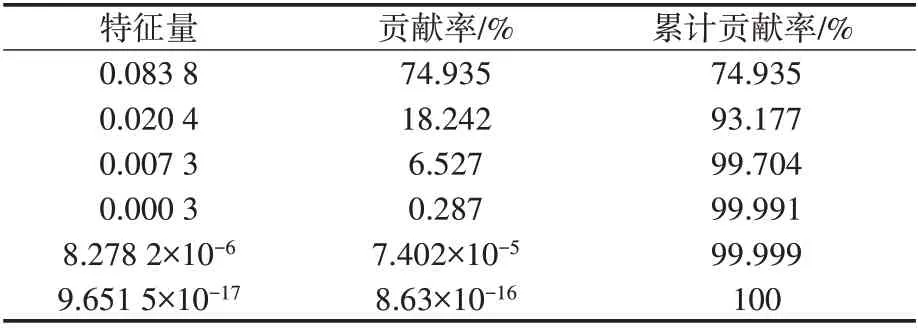
表2 特征值及其贡献率Tab.2 Characteristic values and their contribution rates

如表2 所示，从第3 个特征值之后贡献率已经很小，累计贡献率波动不大。因此，提取前3个特征值就能够代表99.7%的信息，此时将此3 个特征值所对应的特征向量作为最优投影集，经过最优投影后将原始的样本空间的维数降低，这样就能够将偏斜度参量从6 维空间降为3 维。同样对整个统计参量空间进行LDA 数据分析，对特征空间的18个参量进行分析，提取贡献率高且累计贡献率在99.8%的前6个特征值，得到对应的6个特征向量并建立转换矩阵，进行最优投影后将原始特征空间的18维数据降为6维的样本空间。

4 基于优化PNN的局部放电模式识别

4.1 PNN网络结构设计

输入向量的选择：本次GIS 局部放电实验是采用表征图谱特性的特征参数（偏斜度、陡峭度、放电量因数等18 个特征量）经过LDA 方法降维后的6维样本空间作为网络的输入特征量。采用标准化后的特征量作为输入向量，以消除量纲的影响。

输出向量的选择：PNN 网络模式识别的输出层的设计取决于放电类型数，文中模拟了5 类比较典型的GIS 局部放电类型，因此输出层为5 个输出节点且分别对应于模式类别，用于识别局部放电类型。

平滑因子优化：采用遗传算法进行平滑因子的优化，选取种群规模popsize为10，个体长度chromlength取为5，进化次数maxgeneration为50，交叉概率pcross为0.4，变异概率pmutation为0.2，适应度函数误差为0.001。经过遗传算法寻优后，本次实验的平滑因子确定为0.052。

基于LDA 和GA_PNN 分类器的模式识别方法流程图如图10所示，并利用Matlab编程实现：

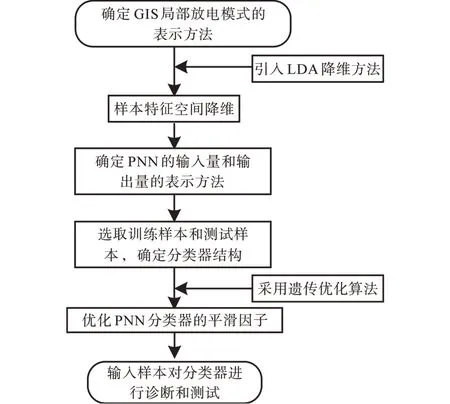
图10 模式识别流程图Fig.10 Flow chart of pattern recognition

1）针对UHF 所检测得到的各类GIS 局部放电类型的特征，确定各局部放电类型的二维图谱，并采用统计特征法提取特征参量；

2）引入线性判别分析对特征空间进行降维处理；

3）依据降维后的样本空间，确定PNN 的输入向量以及输出向量；

4）降维后的特征样本划分为训练样本和测试样本，并依据训练样本确定分类器的结构（各层的神经元个数）；

5）采用遗传算法对PNN 的平滑因子进行优化；

6）将训练样本送入GA_PNN 网络进行模式识别。

4.2 PNN网络结构设计

4.2.1 各放电类型的模式识别

为验证所提出的模式识别方法对局部放电模式的识别效果，从每类缺陷类型的样本集选取30 个测试样本和30 个训练样本，分类进行识别，试验结果如表3 所示。由表3 中的数据可以看出，基于该方法的模式总体识别率达到96.0%，其中有2 类模式存在少量样本的误分类，主要原因是这2类模式的二维图谱存在少量的离散样本。

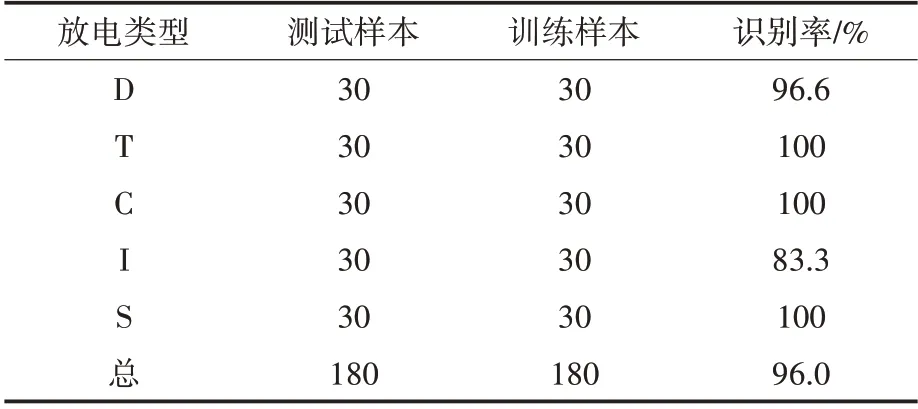
表3 各类模式的识别率Tab.3 Recognition rate of various patterns

4.2.2 不同分类器的识别效果比较

为模拟现实工作中故障的随机性，本次实验从经过降维的5 类共300 个样本中，随机选取150个训练样本和150 个测试样本，模式识别效果图如图11 所示。可以看出，经过训练后，所选取的150 个测试样本中，除了少数的绝缘内部放电类型之外，其余类别都能和其实际的类别对应上，识别率达96.7%。

图11 随机选取测试样本的识别结果Fig.11 Recognition results of randomly selected test samples

利用BPNN，SVM，PNN 和GA_PNN 方法对相同的训练样本和测试样本进行GIS 模式识别。BPNN 的隐节点采用试凑法确定，采用监督学习方式进行权值和阈值的训练，训练目标为0.000 05；大量实验表明，SVM 的核函数选用径向基核函数能够得到较优的结果，扩展常数为1，因SVM是二分类器，因此采用4 个SVM 分类器拓展成五分类器；PNN 的平滑因子采用经验法设为0.1。分别将降维前和降维后的特征样本送入4个分类器进行模式识别，结果如表4和表5所示。

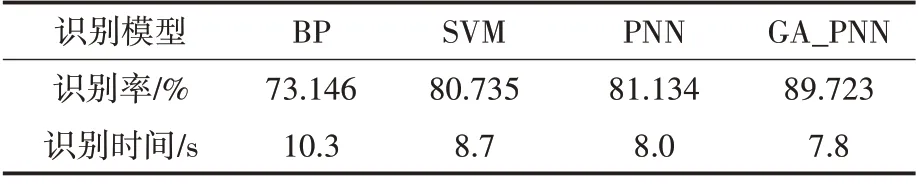
表4 降维前4种识别方法的识别率和识别时间Tab.4 Recognition rate and recognition time of four recognition methods before dimension reduction

由表4 和表5 可知，相比较于降维前的样本数据，各识别方法在处理降维后的特征样本时具有更短的识别时间和更高的识别率。这是因为降维方法提供的低维样本空间便于缩短识别时间，且LDA 降维后的样本空间具有明显的类间信息，能够提高识别率。

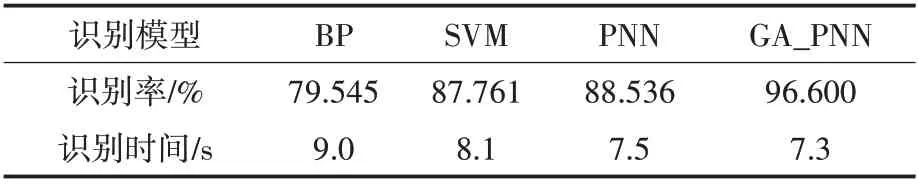
表5 降维后4种识别方法的识别率和识别时间Tab.5 Recognition rate and recognition time of four recognition methods after dimension reduction

由表5 可知，GA_PNN 与PNN 的识别速度快并且相差不多，SVM 的速度次之，BP 网络则需要更多时间。这是由于PNN 网络无需反复训练，SVM 需要求得支撑向量，建立分类超平面，BP 网络则需要多次迭代以更新权值和阈值，且极易陷入局部最优而表现出较差的识别率和识别时间。SVM 和PNN 识别效果相差不大，识别率能够达到88%左右，而经过遗传算法优化平滑因子的PNN方法的识别率能够达到96%，且拥有最短的识别时间。

5 结论

对于GIS 局部放电信号的特性，提出了采用LDA 数据分析方法并结合改进的概率神经网络进行局部放电模式识别。基于GIS 高压实验平台，模拟了5 类典型的GIS 局部放电模式，并采用线性判别分析法对超高频信号的统计特征参量进行降维处理，结合GA_PNN 的识别方法进行局部放电模式识别，并与目前常用的分类方法进行比较，结论如下：

1）对于GIS 局部放电原始信号的特性，采用线性判别分析法对特征空间进行降维处理，得到含有明显类别信息的低维特征空间，提供给PNN识别模型具有类别信息的训练样本，能够有效提高识别率。

2）采用遗传算法对PNN 的平滑因子进行优化，得到适合PD 模式分类的平滑因子，相对于常用的经验法选取的平滑因子而言，优化平滑因子后的PNN 更适合解决GIS 局部放电模式识别问题。

3）采用优化后的PNN 作为模式识别器，分别对降维前和降维后的特征样本进行局部放电模式识别，相比较于常用的BPNN，SVM，PNN 等识别方法，GA_PNN 方法具有较高的识别精度和较快的识别速度。所提方法并不局限于解决GIS设备的局部放电问题，亦适用于其他电气设备的局部放电问题。

4）采用常见的高斯窗函数作为概率密度函数。依据实际问题，选择最佳的窗函数，能够直接影响GIS 局部放电模式的识别结果，该部分研究仍需进一步展开。