引入竞争机制的改进AR谱估计间谐波分析方法

刘海涛，孙放，夏书悦

（1.南京工程学院 电力工程学院，江苏 南京 211167；2.江苏省配电网智能技术与装备协同创新中心，江苏南京 211167）

近年来，随着电力电子技术的迅速发展，电力系统中谐波问题越来越复杂，严重影响了电力设备的安全经济运行。其中，由较大电压波动或冲击性非线性负载引起的间谐波，不仅具有谐波的危害，还会导致次同步震荡、电压闪变及波动等问题。因此，精确地检测和分析间谐波具有非常重要的工程实际意义[1-2]。

针对电力系统中间谐波的分析与检测，众多学者进行了大量研究，并取得了丰硕成果。目前较为常用的间谐波分析方法有很多，包括傅里叶变换、自回归（autoregressive，AR）谱估计法、小波变换法、S 变换法等[3-5]。文献[6]提出了一种小波包变换和快速傅里叶变换相结合的检测方法，从而确定谐波的相位、幅值以及频率信息，但在低频谐波的检测方面误差较大，需要进一步改进算法来得到更加精确的低频谐波参数。文献[7]通过把CEEMD 和改进Prony 相结合实现谐波分量特征参数的有效提取，具有良好的抗噪性能，但是对频率和相位的检测精度较差，间谐波的检测精度偏低。文献[8]提出了一种最优加权Burg 谱估计来分析间谐波，进一步改进了Burg 算法的性能，提高了频率分辨率，但检测间谐波的幅值和相位精度不高。文献[9]将Synchrosqueezing 小波变换应用到电力系统谐波检测中，对连续小波变换的结果进行同步挤压，以此计算电力信号主频率，并结合最小二乘拟合和Hilbert 变换，计算噪声背景下谐波的幅频参数，有效地抑制了噪声的干扰，但在对间谐波频率检测时误差较大，且算法运算量很大。

上述文献的方法在针对间谐波检测方面都有一个共同点：若要最终求得的间谐波参数足够精确，首要的是获得间谐波信号中各个分量的频率，接着再展开下一步的计算。而上述这些方法都很难做到同时兼顾谐波检测的高分辨率和高精度。针对多数谐波检测方法谐波频率精度低的问题，文中采用频率分辨率较高的AR 谱估计法进行求得间谐波频率，但由于AR 谱分析无法精确估计间谐波幅值及相位，因此需要对间谐波的幅值及相位进一步优化。文章基于已有成果，提出了一种具有竞争机制的改进混合遗传粒子群算法，利用AR 谱估计法获取间谐波的阶数和频率，并将间谐波信号幅值编码于改进混合遗传粒子群算法中，最后利用该算法对间谐波的相位及幅值进行参数的估计，进而使谐波检测中参数估计的精确度和抗干扰性得到有效提高。

1 基于AR模型的间谐波谱估计

在现代谱估计中AR 谱估计是较为常用的一种间谐波分析方法，由于其频率分辨率高以及计算量小的特点，得到了广泛的研究和应用[10]。对于一个间谐波信号x（n），其AR模型可以表示为

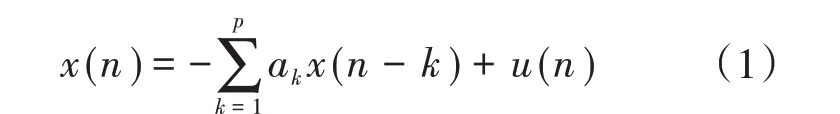
式中：u（n）为白噪声序列；p为AR 模型的阶数；ak（k=1，2，…，p）为AR模型的参数。

由式（1）可得AR模型的Yule-Walker方程：

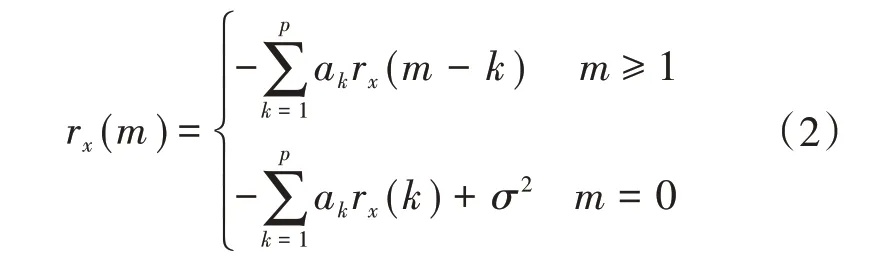
式中：rx（m）为信号x（n）的自相关函数；σ2为白噪声序列的方差。

利用x（n）的前p+1 个相关函数rx（k）（k=0，2，…，p）能够获得AR模型的参数ak，所求参数ak代入式（2）能够得到x（n）的功率谱：

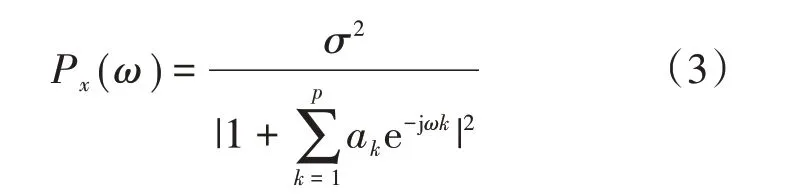
由式（3）可知，若想求得间谐波信号x（n）的功率谱Px（ω），就要求得AR 模型参数ak以及方差。这样，间谐波谱估计可以转化成AR 模型的参数估计问题。

由于相比其他算法，Burg 算法求得的频率分辨率较高且更易实现，因此文中采用该算法求解AR模型参数。p阶前、后向预测误差分别为

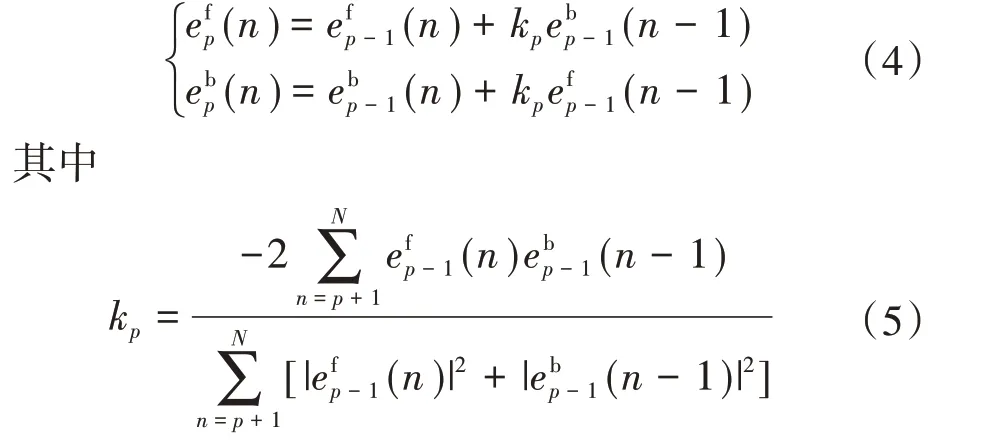
式中：kp为反射系数。

由式（5）求得kp后，再根据Levinson-Durbin 递推公式即可计算AR 模型的参数，进而得到间谐波信号的功率谱密度估计。并且由于使用Levinson-Durbin 递推公式进行计算，使得整体计算的复杂程度低于Prony 法、MUSIC 法等空间谱估计方法。

2 改进混合遗传粒子群算法

粒子群算法（particle swarm optimization，PSO）是一种具有全局搜索能力的智能优化算法，以速度为步长进行迭代寻优，第t+1 代第i个粒子的速度与位置更新的进化方程分别为

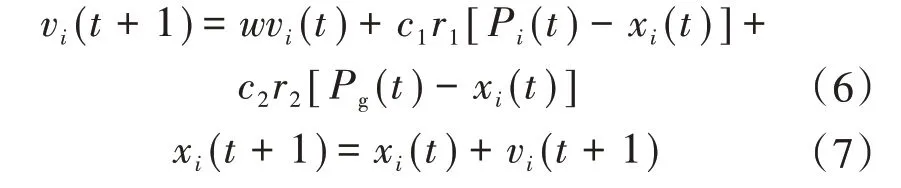
遗传算法（genetic algorithm，GA）也是一种基于生物进化规律而产生的全局搜索智能算法，因此这2 种算法都具有群体优化的优点，但同时自身也存在某种不足和缺陷。对于粒子群算法而言，其实现相对比较简单，迭代求解初期的收敛速度很快，不过随迭代次数的增加，所有粒子都不断地朝最优粒子的方向靠近，导致整个种群很容易陷入局部最优。而遗传算法具有较强的全局搜索能力，但操作较复杂且后期搜索效率较低。基于2种算法的优缺点，人们尝试将两者结合，进行取长补短，研究出性能更为优越的算法[11]。

目前，遗传算法与粒子群算法主要有2 种结合方式。一种是将2种算法以同等地位混合，即串联和并联。串联是指在每一代进化过程中对所有个体依次进行遗传操作及粒子群优化，并联则是在进化过程中使两种算法各计算1/2。文献[12]提出了一种遗传算法和粒子群算法结合的多子群分层串联混合算法（hybrid genetic algorithm and particle swarm optimization，HGAPSO），采用分层结构，一系列遗传算子组成底层，每个子群最优个体的精英群组成上层，但是相比标准粒子群算法，这种方法增加了近1 倍的计算量。另一种是把遗传算子引入到粒子群算法中，以提高算法寻优能力。文献[13]将选择算子引入到粒子群算法中，一定程度提升了收敛速度，但由于选择机制的影响，种群的多样性有明显的降低。文献[14]将变异算子引入到粒子群算法中，虽然在一定程度上增加了种群的多样性，但并不足以改变群体优化的本质特征。

基于淘汰和精英学习的策略提出了一种具有竞争机制的改进混合遗传粒子群算法，通过筛选精英粒子、淘汰劣质粒子，同时在精英粒子间互相学习，以获取最优粒子。实验表明，采用这种竞争策略不仅避免了粒子易陷入局部最优和搜索能力欠佳等问题，还显著提升了算法的求解精度。其操作方式主要由排序、选择、交叉以及变异4部分组成，具体内容包括：

1）排序操作。在每次迭代的过程中，通过适应度值对粒子进行比较并排名，以此来确定该粒子是否为精英粒子，即将前50%的粒子标记为精英粒子，保存并记录该精英粒子群体，将后50%的粒子标记为劣质粒子并淘汰剔除。

2）选择操作。由于在排序操作中剔除了劣质粒子群体，使得粒子群体规模减少了1/2，因此需要对淘汰的粒子群体进行补充使群体规模完整。为了获得高质量的粒子以补充淘汰粒子，采取优中选优的方式选取父代，即从精英粒子群体中随机选择2 个粒子进行适应度值比较，并记录适应度值较小的粒子，作为父代parent1，采取同样的操作选取出父代parent2，进行交叉而获得子代作为新生的生命体，并对淘汰的粒子群体进行补充。

3）交叉操作。对2 个父代进行交叉操作，具体操作表达式为

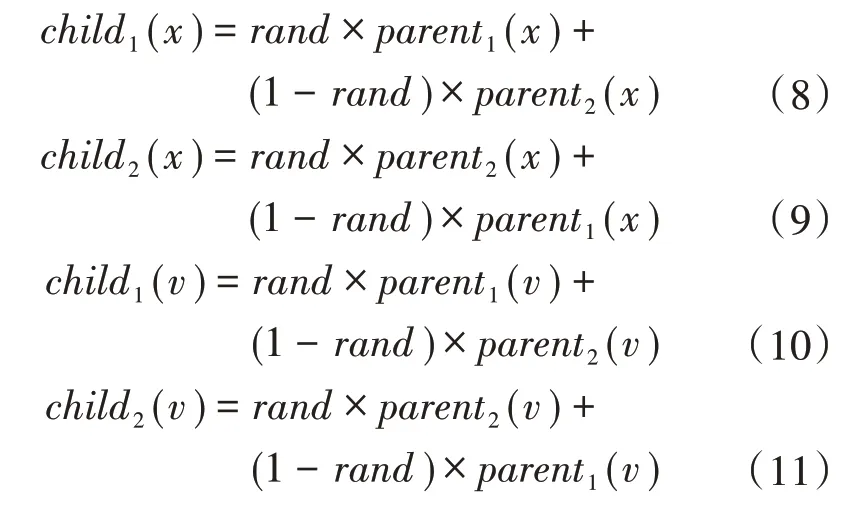
式中：child1（x），child2（x）分别为父代parent1（x）和parent2（x）经过交叉产生的子代粒子位置；rand为0～1 之间均匀分布的随机数；child1（v），child2（v）分别为父代parent1（v）和parent2（v）经过交叉产生的子代粒子速度。

检查更新后的速度与位置是否超出范围，超出范围的取边界值。

4）变异操作。种群的变异操作能够恢复粒子或者再次开发粒子的遗传物质，以防止粒子在求解过程中出现早熟收敛。文中采用的变异方式为

改进HGAPSO算法基本步骤如下：

步骤1：确定算法的种群规模N、搜索维度d、惯性权重w、加速系数c1和c2、迭代次数k；

步骤2：在求解问题定义范围内随机初始化每个粒子的速度和位置；

步骤3：通过适应度值对每个粒子进行升序排序，确定出精英粒子群体和淘汰粒子群体；

步骤4：根据选择操作确定父代粒子，通过式（8）～式（11）进行交叉计算，直到种群规模完整为止，并更新该部分粒子的个体历史最优值和全局最优值；

步骤5：通过式（6）、式（7）更新精英粒子的个体历史最优值和全局最优值；

步骤6：通过式（12）对所有粒子进行相应的变异处理，更新粒子群体的个体历史最优值和全局最优值；

步骤7：判断是否满足条件，满足则输出结果，否则返回步骤3。

3 基于改进HGAPSO 算法的AR 谱估计法

间谐波信号模型如下：

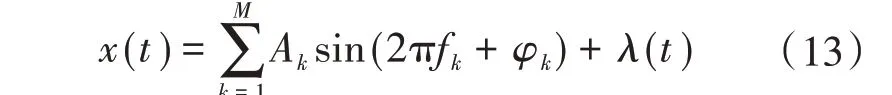
式中：M为信号模型的阶数；Ak，fk，φk分别为第k个谐波分量的幅值、频率和初相位；λ（t）为方差为σ2的白噪声。

根据三角公式，式（13）可变为

通过式（14）将幅值和初相位的分析转化为参数ak和bk的计算。经过改进HGAPSO算法实现幅值参数ak，bk的优化计算，即把所求参数ak，bk编码于粒子群的位置当中。在一定的谐波分析时间Ta下，使粒子群的目标函数值F最小，即

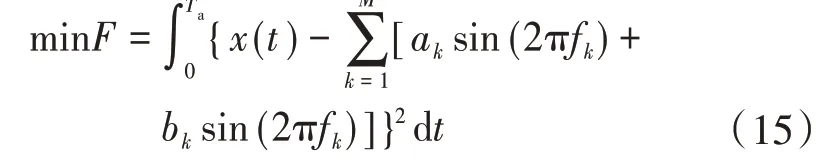
改进HGAPSO 算法基于式（15）进行优化计算后，获得幅值参数ak，bk的估计值，并通过下式计算出幅值Ak和初相位φk：

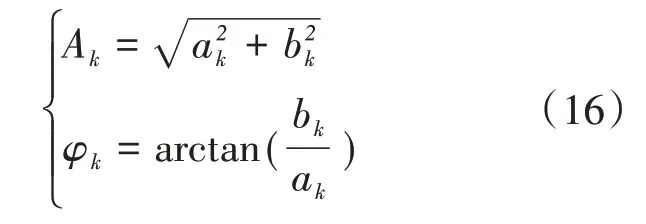
结合AR 谱估计法获得谐波频率及阶数后，使用改进HGAPSO 算法对间谐波进行分析计算。图1 为AR 谱估计结合改进HGAPSO 算法进行间谐波分析的流程图。

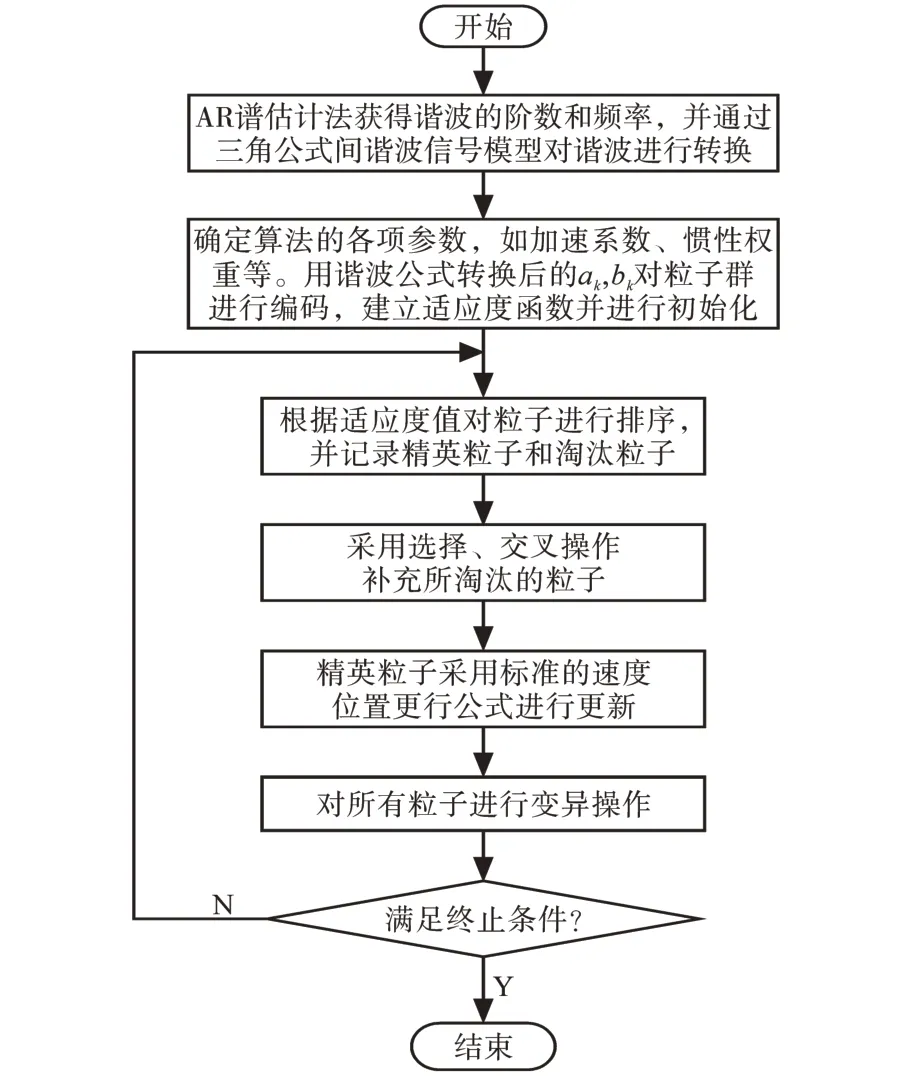
图1 基于AR谱估计和改进HGAPSO算法进行间谐波分析的流程图Fig.1 Flow chart of inter-harmonic analysis based on AR spectral estimation method and improved HGAPSO algorithm

4 算例分析

4.1 简单间谐波信号参数检测

考虑简单间谐波信号如下：

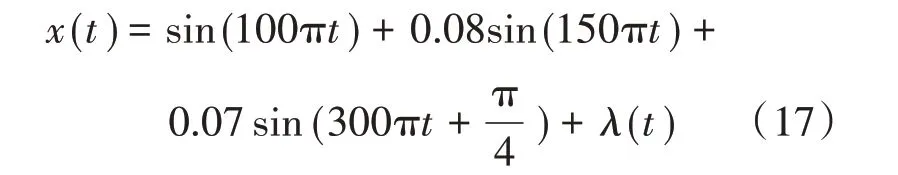
式中：λ（t）为白噪声，信噪比40 dB。

表1 和表2 分别为使用AR 谱估计、插值FFT及加窗BT谱分析谐波频率和幅值的估计结果。

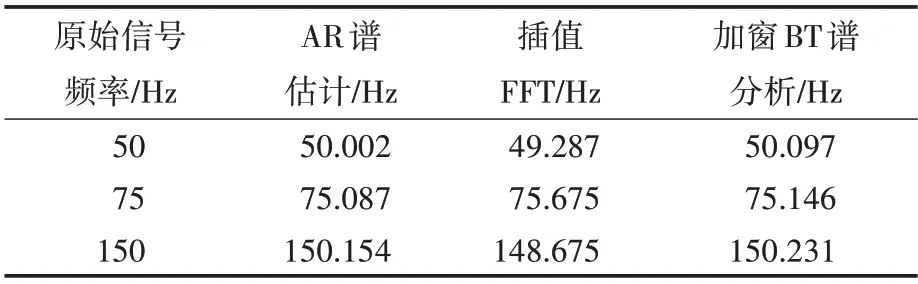
表1 AR谱估计、插值FFT及加窗BT谱分析的谐波频率估计结果Tab.1 Analysis result of harmonic frequency with AR spectral，interpolation FFT and windowed BT spectral estimation

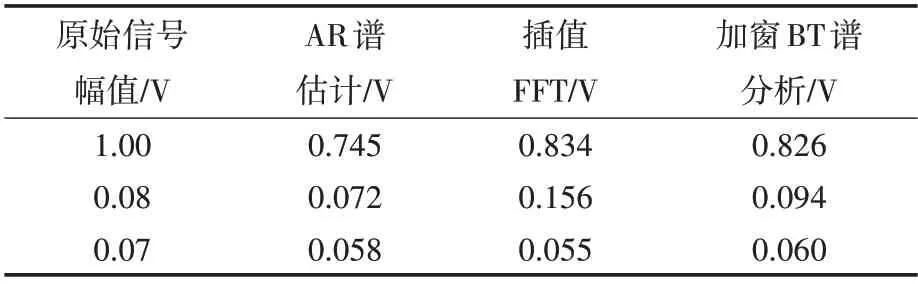
表2 AR谱估计、插值FFT及加窗BT谱分析的谐波幅值估计结果Tab.2 Analysis result of harmonic amplitude with AR spectral，interpolation FFT and windowed BT spectral estimation

从表1 可以看出，与插值FFT 以及加窗BT 谱分析相比，使用AR 谱估计法能够获得较高的频率分辨率，但从表2 的谐波幅值估计结果发现其幅值分析出现了较大误差。因此本文旨在AR 谱估计获得较高频率分辨率的基础上，采用智能算法对谐波的幅值和初相位进行优化计算。

4.2 复杂间谐波信号参数检测

4.2.1 无噪声干扰下的间谐波参数检测考虑无噪声干扰下的复杂间谐波信号如下：

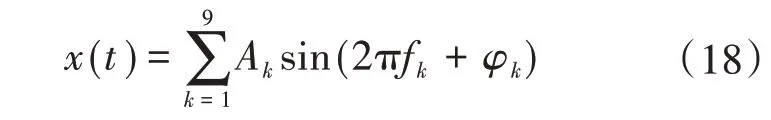
式（18）中各谐波、间谐波的频率、幅值和初相位如表3所示。

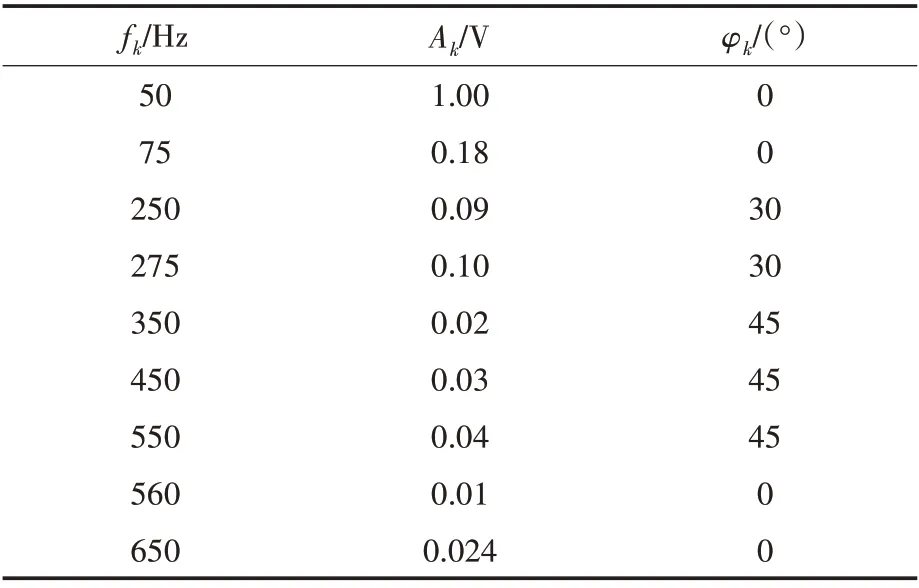
表3 谐波及间谐波参数Tab.3 Harmonic and inter-harmonic parameters

取采样频率2 000 Hz、采样点数1 024、频率细化插入点数100，分别采用文中提出的改进HGAPSO 算法、HGAPSO 算法、标准PSO算法和标准GA 算法对谐波模型进行优化。优化参数具体设置为：粒子数目50，迭代步数500，w=0.729 8，c1=c2=1.494 4，搜索范围ai，bi∈[-1，1]，i=1，2，…，9。粒子在每次迭代过程中通过计算目标函数的最佳适应度值，进而获得谐波的幅值和初相位，迭代收敛曲线如图2所示。

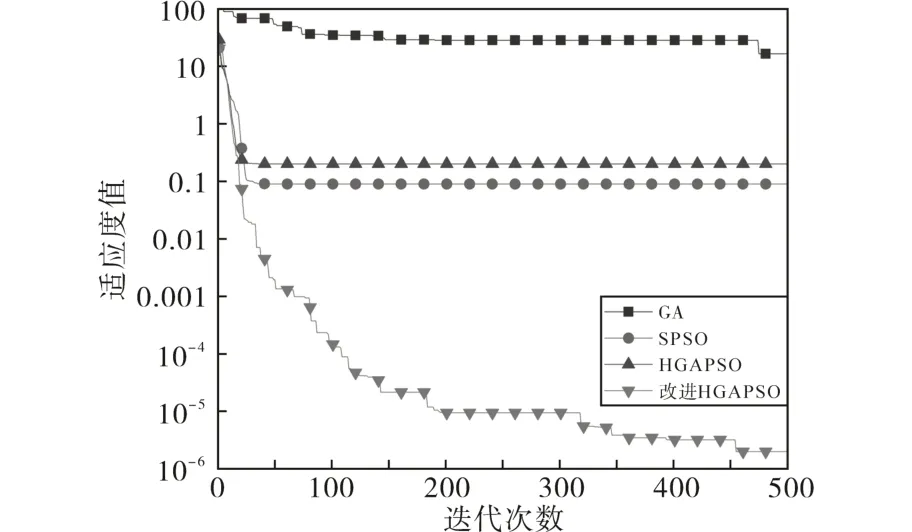
图2 4种算法迭代收敛曲线Fig.2 Iterative convergence curves of four kinds of algorithms

从图2 可以看出，随着迭代的增加，改进HGAPSO 算法适应度值呈现持续下降的趋势，并在第500 步迭代终止时收敛到10-6数量级，达到了较高的精确度。而其他3种算法从迭代初始便陷入了局部最优，最终PSO 算法和HGAPSO 算法的适应度函数值下降了3个数量级，而GA算法仅下降了2个数量级。因此文中提出的改进HGAPSO 搜索速度更快，适应度值的数量级远超于HGAPSO 算法、PSO 算法和GA 算法，对谐波的幅值和初相位的计算具有明显的优势。仿真结果如表4～表7所示。

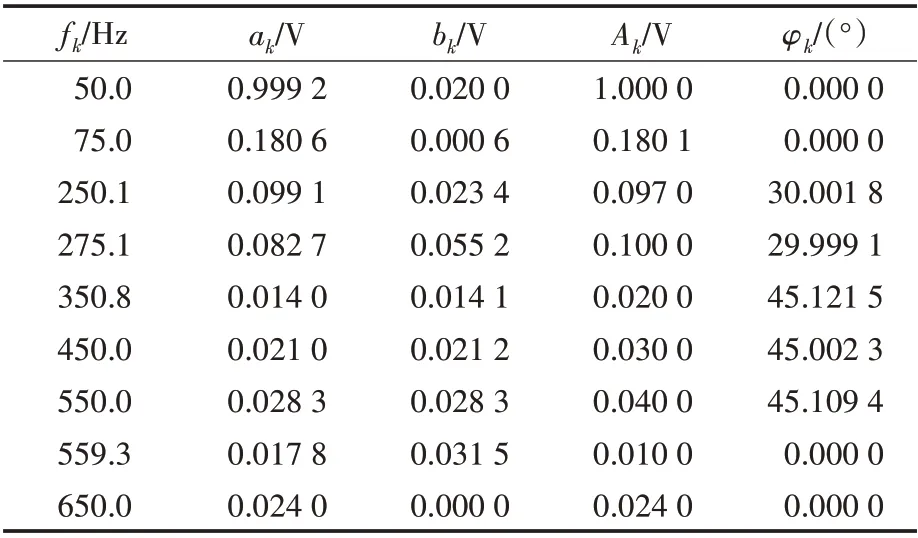
表4 基于改进HGAPSO算法谐波和间谐波参数的仿真结果Tab.4 Simulation results of harmonic and inter-harmonic parameters based on improved HGAPSO algorithm

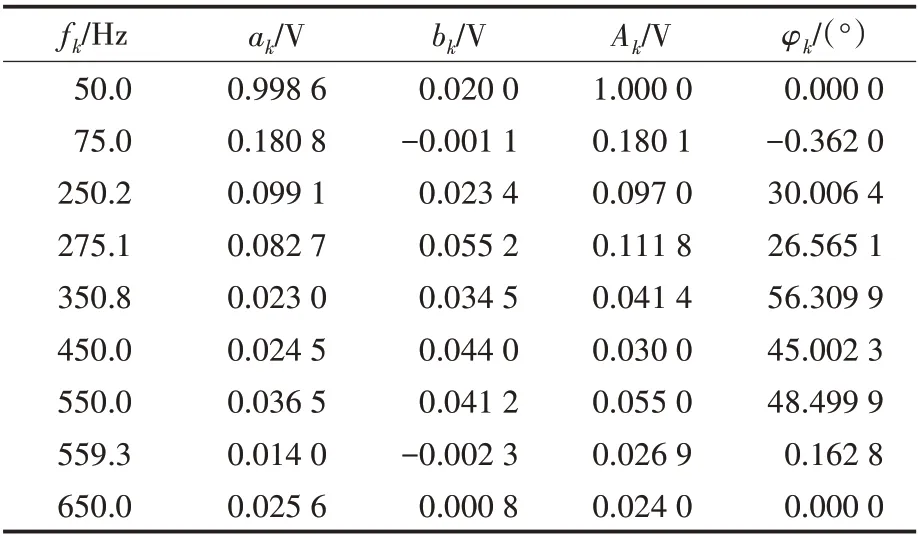
表5 基于HGAPSO算法谐波和间谐波参数的仿真结果Tab.5 Simulation results of harmonic and inter-harmonic parameters based on HGAPSO algorithm

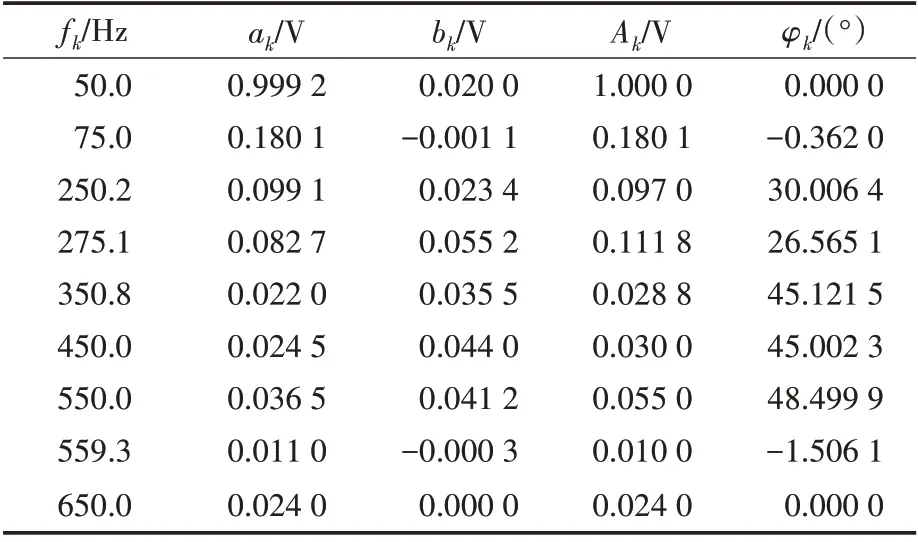
表6 基于PSO算法谐波和间谐波参数的仿真结果Tab.6 Simulation results of harmonic and inter-harmonic parameters based on PSO algorithm

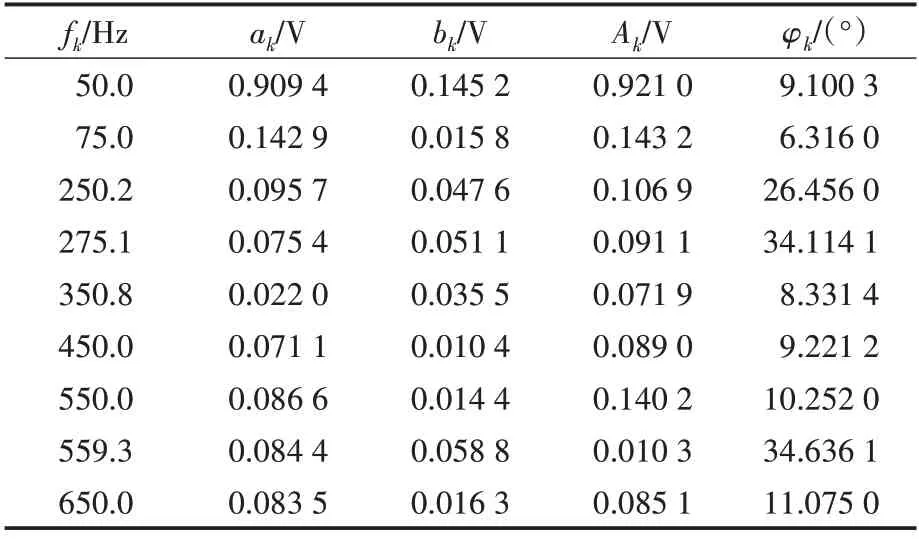
表7 基于GA算法谐波和间谐波参数的仿真结果Tab.7 Simulation results of harmonic and inter-harmonic parameters based on GA algorithm

由表4～表7 可以看出，文中提出的改进HGAPSO 算法能有效地估计9 个谐波分量的幅值和初相位。其对于幅值和初相位的求解精度明显高于采用HGAPSO 算法、PSO 算法和GA 算法。4种算法幅值和初相位误差如表8所示。

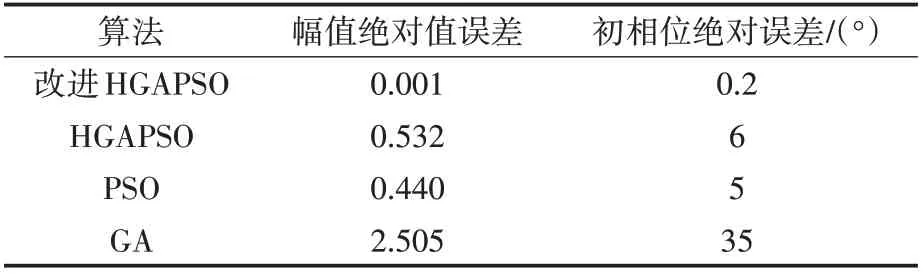
表8 幅值和初相位误差Tab.8 Errors of amplitude and initial phase

从表8 可以看出，改进HGAPSO 算法优化后幅值的绝对值误差和初相位绝对误差也明显低于其他3种优化算法。可以发现，使用PSO算法对幅值和谐波进行优化计算时，计算精度明显要高于GA算法，总体来看，对于谐波的优化计算使用PSO算法更加合适，并且能够达到工程的实际要求。

4.2.2 噪声干扰下的谐波和间谐波参数检测

实际工程中，谐波的分析通常伴有噪声存在，故在算例4.2.1 复杂间谐波信号中加入随机噪声λ（t）进行仿真实验。定义间谐波参数的综合误差Et如下式：

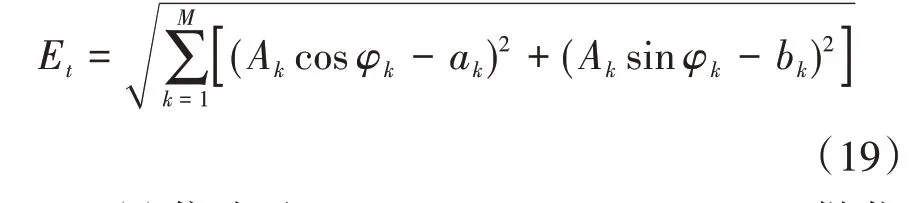
λ（t）依次取0.01，0.02，0.03，0.04，0.05 做仿真试验，随机噪声对间谐波综合误差的影响如表9所示。

从表9 可以看出，随着随机噪声值的不断增加，间谐波估计参数的综合误差不断增加，说明随机噪声的增加对算法分析谐波的精度具有一定的影响。经过比较可知，改进HGAPSO 算法的求解精度明显强于其他几种算法。

表9 随机噪声对间谐波综合误差的影响Tab.9 Effects of random noise on inter-harmonic combined error

5 结论

1）AR 谱估计法具有较高的频率分辨率，同时可较准确分辨信号中所含间谐波的个数，但是对谐波的幅值和相位计算误差较大，因此不能单独使用AR谱估计法对谐波各参数进行分析。

2）基于淘汰和精英学习的策略，提出了一种具有竞争机制的改进HGAPSO 算法，并将其与其他3 种算法的仿真结果进行比较。结果表明，改进HGAPSO 算法可以较好地实现间谐波幅值和相位的参数优化，间谐波参数的综合误差Et低于3%，且该算法求解精度更高，能够有效地逃避局部最优，具有强健的稳定性。

3）采用AR 谱估计法和改进HGAPSO 算法相结合的谐波分析策略，能够有效地分析谐波频率、幅值及初相位，求解精度较高且易于实现。但在实际求解过程中，由于使用群体智能算法的影响，使得谐波分析时间较长，因此，如何加快谐波分析效率仍然是今后需要研究的问题。