基于机器学习的蠕变断裂寿命预测方法

张效成,宫建国,轩福贞

(华东理工大学 机械与动力工程学院 承压系统与安全教育部重点实验室，上海 200237)

0 引言

数世纪以来，科学的发展经历了4个阶段，第一个阶段为经验科学阶段，在此阶段，人们通过基于经验及试验认识世界；第二个阶段为理论科学阶段，在此阶段一系列定理被提出；第三个阶段为计算科学阶段，这一阶段主要受益于计算机科学的发展，结合第二个阶段的理论模型可以描述复杂的现象；第四个阶段为数据驱动科学阶段，得益于数据量的激增，数据驱动的方法为解决传统问题提供了可替代的方案[1]。

对于复杂的工程问题，往往难以直接得到解析解，而经验解无法描述高维数据之间复杂的非线性交互关系。机器学习作为数据驱动的解决方案，可以克服解析解和经验解的局限性，为复杂工程问题提供解决方案。当前，已有许多研究人员利用机器学习的方法解决裂纹缺陷预测及断裂韧性计算等领域的难题。ROVINELLI等[2]将原位试验、晶体塑性模拟及贝叶斯网络结合，确定了多晶材料小疲劳裂纹扩展的方向及速率；FENG等[3]在小数据集下，利用深度神经网络实现了材料硬化裂纹敏感性的预测；TONG等[4]使用决策树、支持向量机及朴素贝叶斯等多种机器学习模型，预测了多晶镁合金在变形之前的孪晶形核行为；HU等[5]结合Markov链Monte Carlo算法及高斯过程回归算法，提高了涡轮盘疲劳裂纹扩展寿命的预测精度，并且对预测结果的不确定性进行了量化；LIU等[6]将有限元计算结果与回归树、人工神经网络等机器学习算法结合，显著提高了显微多晶硅断裂韧性的计算效率。由此可见，机器学习为传统复杂工程问题提供了另一种解决方案。

工程部件的寿命预测问题是高温结构完整性领域的重要课题，而蠕变寿命预测是其中的重要组成部分[7-14]。影响蠕变断裂寿命的因素包括材料类型、材料型式、热处理、化学成分、温度及应力等[15]。常用蠕变断裂寿命预测经验公式仅考虑了应力及温度的影响，预测模型泛化能力较差，而机器学习方法实现了大量数据的训练与预测，可为结构蠕变寿命预测提供新的解决方案。图1从模型类型、输入变变量等角度比较了两种不同的蠕变寿命预测方法。本研究基于高维输入属性数据，利用BP神经网络、支持向量机、随机森林及高斯过程回归等机器学习方法，对316奥氏体不锈钢的蠕变断裂寿命进行预测。

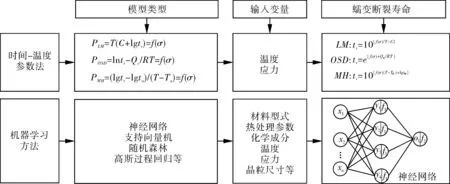
图1 传统时间-温度参数法与机器学习方法对比

本文主要介绍机器学习方案的建立方法、数据集的收集及预处理、所选用的机器学习模型，以及基于机器学习的蠕变断裂寿命预测结果。

1 机器学习方案建立方法

本研究提出了基于机器学习的工程问题解决方案，尤其是针对结构完整性领域的寿命预测问题。在寿命预测领域，由于影响寿命的因素较多，解析解往往基于大量简化假设，导致预测精度有限；而经验解往往无法描述影响因素之间存在的复杂交互关系，机器学习方案可以克服两者的局限性。

使用机器学习的方法解决工程问题可分为4步(如图 2所示):第一步是确定目标变量及输入变量，判断输入变量的类型需要以问题的物理机理及试验观察为基础，尽量避免考虑对目标无影响的变量，减小计算量;第二步是构建数据集，机器学习本质上是一种数据驱动的解决方案，因此理论上讲数据量应尽可能多，另一方面，收集数据时应当初步对数据质量进行判断，剔除明显的离群值，避免引入不必要的噪声;第三步是选用机器学习模型，基于问题的类型(聚类/降维/分类/回归)，选择合适的机器学习模型，进行调参训练；通常难以直接选出最优的机器学习模型，需要同时建立多种机器学习模型的解决方案，基于不同模型的预测结果，进而判断最优的机器学习模型;第四步是共享机器学习解决方案，机器学习解决方案的显著优势在于易于共享及维护，在社区内部共享工程问题的解决方案，一方面可以源源不断地补充新的数据，进一步提高机器学习方案的泛化能力,另一方面，可以对机器学习算法进行优化，提高模型的表达能力。

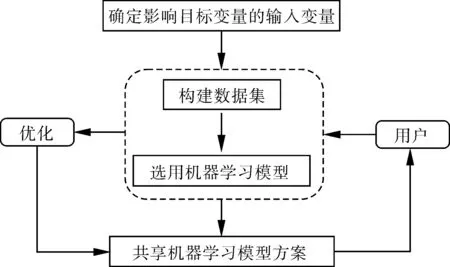
图2 机器学习方案的建立及优化流程

本文基于所提出的机器学习方法，使用BP神经网络、支持向量机、随机森林及高斯过程回归等机器学习模型，开展了316奥氏体不锈钢蠕变断裂寿命预测研究。

2 数据收集及预处理

2.1 数据收集

316奥氏体不锈钢数据来源于日本NIMS蠕变数据库[16-18]。该数据库提供了大量316奥氏体不锈钢蠕变断裂数据，并且提供了试样及试验条件的详细信息，包括材料型式(棒材、板材及管材等)、热处理温度及保温时间、化学成分、温度和应力等。本研究共使用317组数据，包括：棒材数据166组、板材数据57组、管材数据94组。表1列出了部分316奥氏体不锈钢的蠕变断裂数据。数据集内最短蠕变断裂寿命为29.2 h，最长蠕变断裂寿命为173 814.3 h。数据集总体寿命分布如图3所示，可以看出，数据集蠕变断裂寿命基本在100 000 h以内，在不同区间内寿命分布较为均匀。

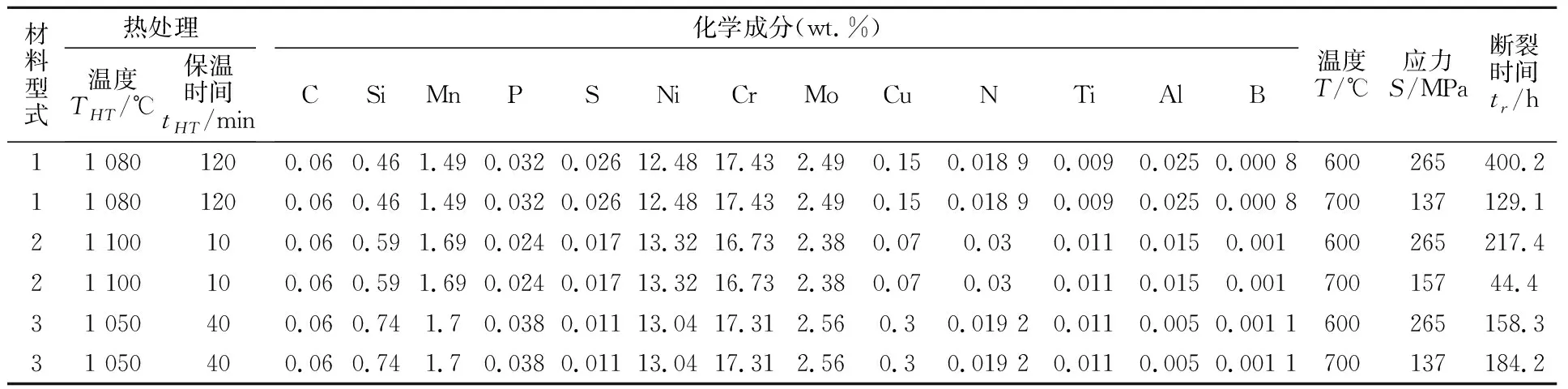
表1 部分316奥氏体不锈钢蠕变断裂数据

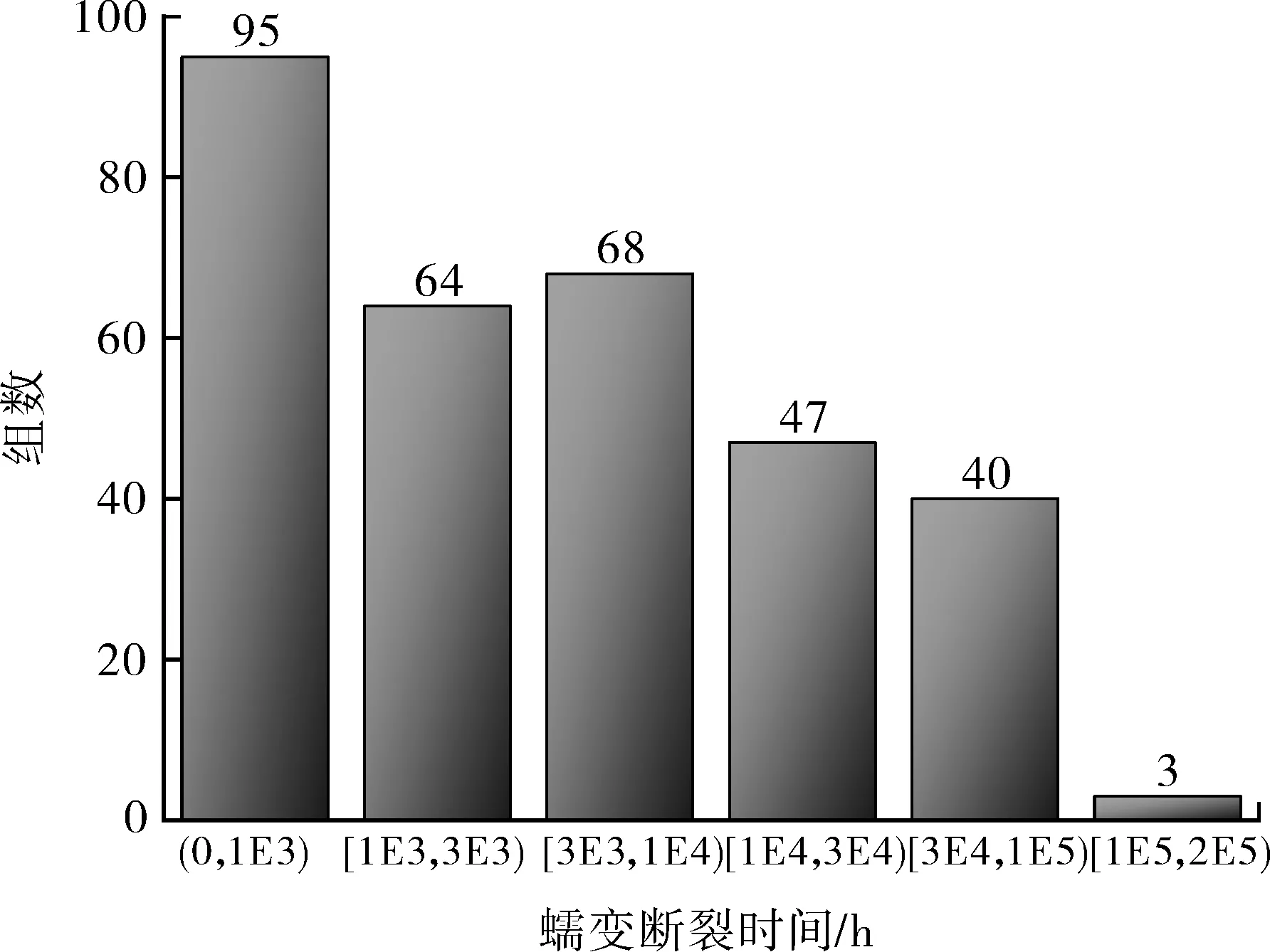
图3 蠕变断裂寿命分布

2.2 敏感性分析

利用相关系数研究不同输入变量对蠕变断裂寿命的影响，其计算公式如下：

(1)

式中，Cov为协方差;Xi为属性(i=1,…,18);Y为蠕变断裂时间，h;Var为方差。

相关系数越接近1，说明该变量对蠕变断裂寿命的影响越大。

图4示出不同属性与蠕变断裂寿命之间的相关系数。可以看出,试验温度、应力、C/Ni/N元素含量及热处理保温时间等属性对蠕变断裂寿命的影响较大。但是，所有输入属性的相关系数均小于0.3，这说明蠕变断裂寿命受到多种输入属性的非线性交互作用，少量输入属性无法准确建立与蠕变断裂寿命之间的联系。

图4 输入属性与蠕变断裂寿命之间的相关系数

2.3 数据降维

当数据集属性维度较高时，可以使用主成分分析(PCA)将输入属性映射到低维空间，一方面可以减小输入维度，提高运算速度；另一方面保留输入属性的主要信息，舍弃部分必要信息，达到降噪的目的。如图 5所示，18类输入属性经过PCA处理后缩减为4类主成分，第一主成分与第二主成分可以表达原始输入属性90%以上的信息。结合主成分分析与机器学习方法，可以在保留大部分输入属性信息的同时，显著提高计算速度。

图5 不同主成分及其贡献率

2.4 数据前处理

为减小属性值大小对模型训练的影响、提高训练速度，需要对输入属性值进行归一化，即将不同类别属性值转换到相同大小的区间内。本研究将输入属性值转换到0～1的区间内。

在使用数据集训练模型之前，首先需要将数据集随机划分为训练集和测试集。使用训练集训练模型，使用测试集评估模型的预测性能。本研究按照8∶2将数据集划分为训练集和测试集，即训练集数据为254组，测试集数据为63组。

3 机器学习模型选用

针对不同的实现目标，机器学习算法可分为4类：属于无监督学习算法聚类、降维及属于监督学习算法的回归、分类。对于寿命预测问题，应采取合适的回归学习算法，常用的回归学习算法包括神经网络、支持向量机、随机森林及高斯过程回归等。

3.1 BP神经网络

神经网络是具有适应性的简单单元组成的并行互联网络，模拟生物神经系统对外界的响应[19-20]。BP(Back Propagation)神经网络是McClelland和Rumelhart在1986年提出的一种误差反向传播的前馈神经网络[21]。神经网络的基本单元是神经元，每个神经元与其他神经元相连，进行信号传递。神经网络的基本结构包括输入层、隐含层及输出层。基于隐含层的数量可分为单层神经网络及多层神经网络。单层BP神经网络的结构如图6所示，输入信号通过一定的权重、偏置及激活函数处理，经过隐含层传递给输出层。若输出与期望输出不一致，则进入误差反向传播过程，基于反向传播算法使得损失函数最小化，从而得到最优的权重与偏置，完成模型训练。

图6 单隐含层BP神经网络结构

3.2 支持向量机

支持向量机(Support Vector Machine，SVM)最初针对的是二分类问题，后来提出核函数，通过非线性变换实现了高维空间的线性可分，解决了高维空间的分类问题[22]。

SVM分类的核心思想是寻找最优分类面，使得样本间隔最大。在SVM分类的基础上，引入不敏感损失函数，从而将其用于解决回归问题，其目标变为寻找最优分类面使得样本离分类面误差最小。SVM的核心部分在于核函数，常用核函数包括多项式核、高斯核(也称径向基核)及Sigmoid核等，其表达式及参数如表2所示。

表2 常用核函数

3.3 随机森林

随机森林利用Bootstrap重采样方法从样本中抽取多个样本，然后利用决策树对每个Bootstrap样本进行决策树建模，将多个决策树的预测结果进行组合，所得预测结果即为随机森林模型的预测结果，其本质上是一种多决策树组合模型[23-24]。决策树具有树形结构，采用自顶向下的递归方式，从根节点开始，在内部节点比较属性值，最后在叶子节点上得到结论，基本结构如图7所示。在决策树中，使用信息熵度量样本集合纯度，从而判断节点属性类别。决策树是一种白箱模型，可以推出明确的逻辑表达式。

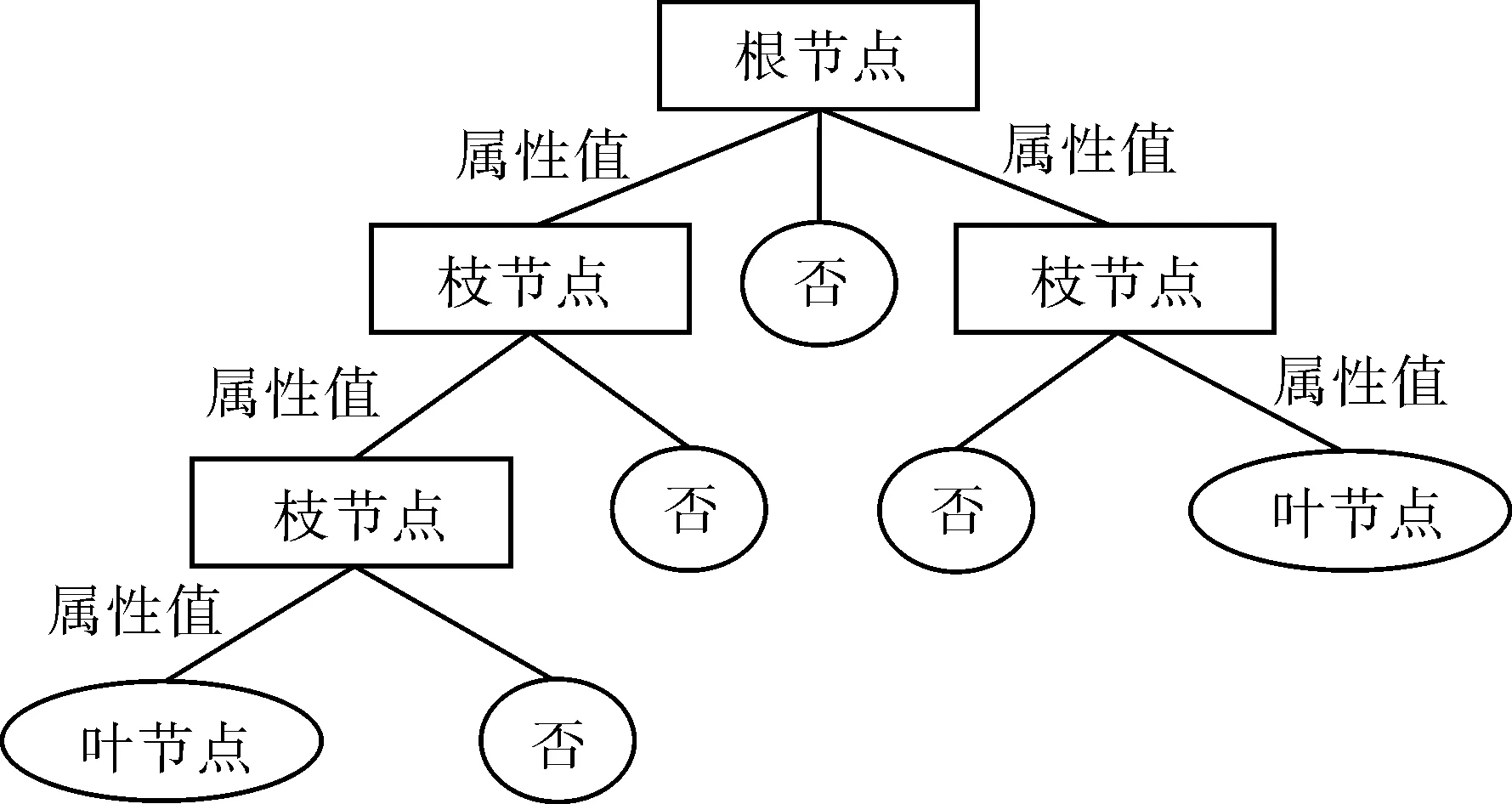
图7 决策树基本结构

3.4 高斯过程回归

高斯过程回归(Gaussian Process Regression,GPR)是使用高斯过程先验对数据进行回归分析的非参数模型。高斯过程是指一组随机变量的集合，在此集合里面任意有限个随机变量均服从联合正态分布[25]。其性质由均值函数和协方差函数确定：

(2)

式中,x,x′为任意随机变量。

GPR模型假设包括噪声(回归残差)和高斯过程先验两部分，其求解按贝叶斯推断进行。高斯过程回归模型如下：

y=f(x)+δ

(3)

可以得到试验值y的先验分布：

(4)

试验值及预测值的联合先验分布为：

(5)

式中，K(X,X)为n×n阶协方差矩阵；In为n阶单位矩阵；K(X,x*)为测试点x*与训练集输入X之间的协方差矩阵；k(x*,x*)为测试点x*的自身协方差。

基于贝叶斯推断，可以计算出预测值的后验分布：

(6)

其中：

(7)

Cov(f*)=k(x*,x*)-K(X,x*)[K(X,X)

(8)

高斯过程使用了贝叶斯技巧，得到的模型属于非参数概率模型，其优势主要表现在于不仅能够对未知输入进行预测输出，而且能够对预测输出的不确定性(即估计方差)进行定量分析。

4 结果及讨论

4.1 Larson-Miller模型

Larson-Miller参数法是最具代表性的时间-温度参数(TTP)法，在工程上被广泛用于蠕变断裂寿命预测[26-27]。Larson-Miller参数表达式如下：

PLM=(T+273)(C+lgtr)=a(lgS)2+blgS+c

(9)

式中，PLM为Larson-Miller参数；T为温度，℃；C为Larson-Miller常数；tr为蠕变断裂时间，h；S为应力，MPa；a，b，c为拟合参数。

使用测试集中试验值及对应预测值之间的决定系数衡量模型的预测精度，用R2表示，该值越大说明精度越高，R2最大值为1，计算方法如下：

(10)

式中,Ypre为预测寿命;Yex为试验寿命。

比较不同C值对应的决定系数，发现C=17时决定系数最高，其值为0.618。图8为蠕变断裂寿命试验数据及Larson-Miller拟合曲线，可以发现不同温度下的蠕变断裂数据在时间-应力坐标系下表现出较大的分散性，Larson-Miller拟合曲线可以描述大量试验数据的平均行为，但无法解决试验数据的分散性问题，预测精度有限。

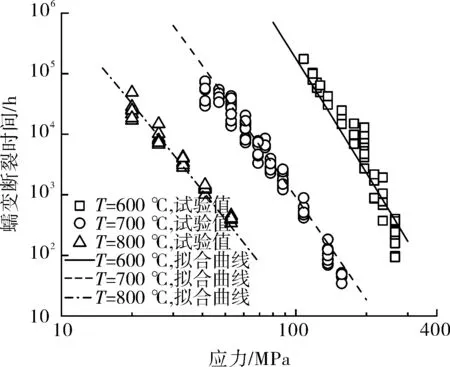
图8 Larson-Miller拟合曲线及蠕变断裂寿命试验数据

4.2 BP神经网络

隐层神经元数量、激活函数类型及反向传播算法等参数会显著影响BP神经网络模型预测能力。控制BP神经网络参数，选用18维输入属性数据训练模型，并且基于测试集选择确定最优的参数。如图9所示，当隐层神经元数量为4时，预测精度较高，增加隐层神经元数量并不一定能够改善预测精度。选用tansig隐含层激活函数的预测精度略优于logsig函数。LM(Levenberg-Marquardt)反向传播算法不仅具有较快的训练速度，而且较之GD(Gradient descent)算法和GDA(Gradient descent with adaptive learning rate)算法具有更高的预测精度。

图9 不同隐层神经元数量、隐含层激活函数及 反向传播算法的预测精度

改变数据集属性种类数，分别使用18类属性、2类属性(温度T及应力S)及4类输入属性(第一类至第四类主成分)的数据集进行蠕变断裂寿命预测，预测精度如图10所示。当输入属性类别为18时，测试集决定系数可达0.967，显著高于输入属性类别为2和4的决定系数，这表明BP神经网络可以捕捉多输入属性与蠕变断裂寿命之间隐含的关系，使用多类输入属性数据集进行蠕变寿命预测可以降低预测结果的分散性，提高预测精度。

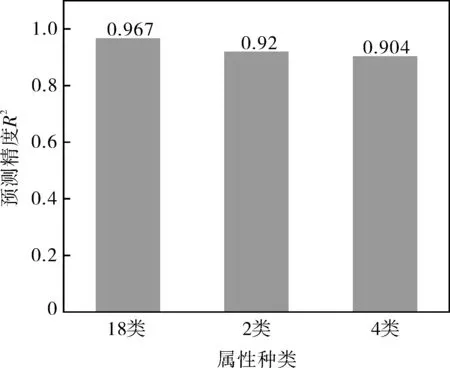
图10 不同属性数目数据集下的BP神经网络预测精度

使用BP神经网络(18类属性)与Larson-Miller模型对测试集数据集进行蠕变断裂寿命预测，结果如图11所示，BP神经网络决定系数为0.967，Larson-Miller模型决定系数为0.708，BP神经网络预测精度高于Larson-Miller模型。当蠕变断裂寿命小于10 000 h时，两者的预测精度相似，但随着蠕变断裂寿命的增加，Larson-Miller模型的预测精度显著下降，而BP神经网络则一直保持较高的预测精度。

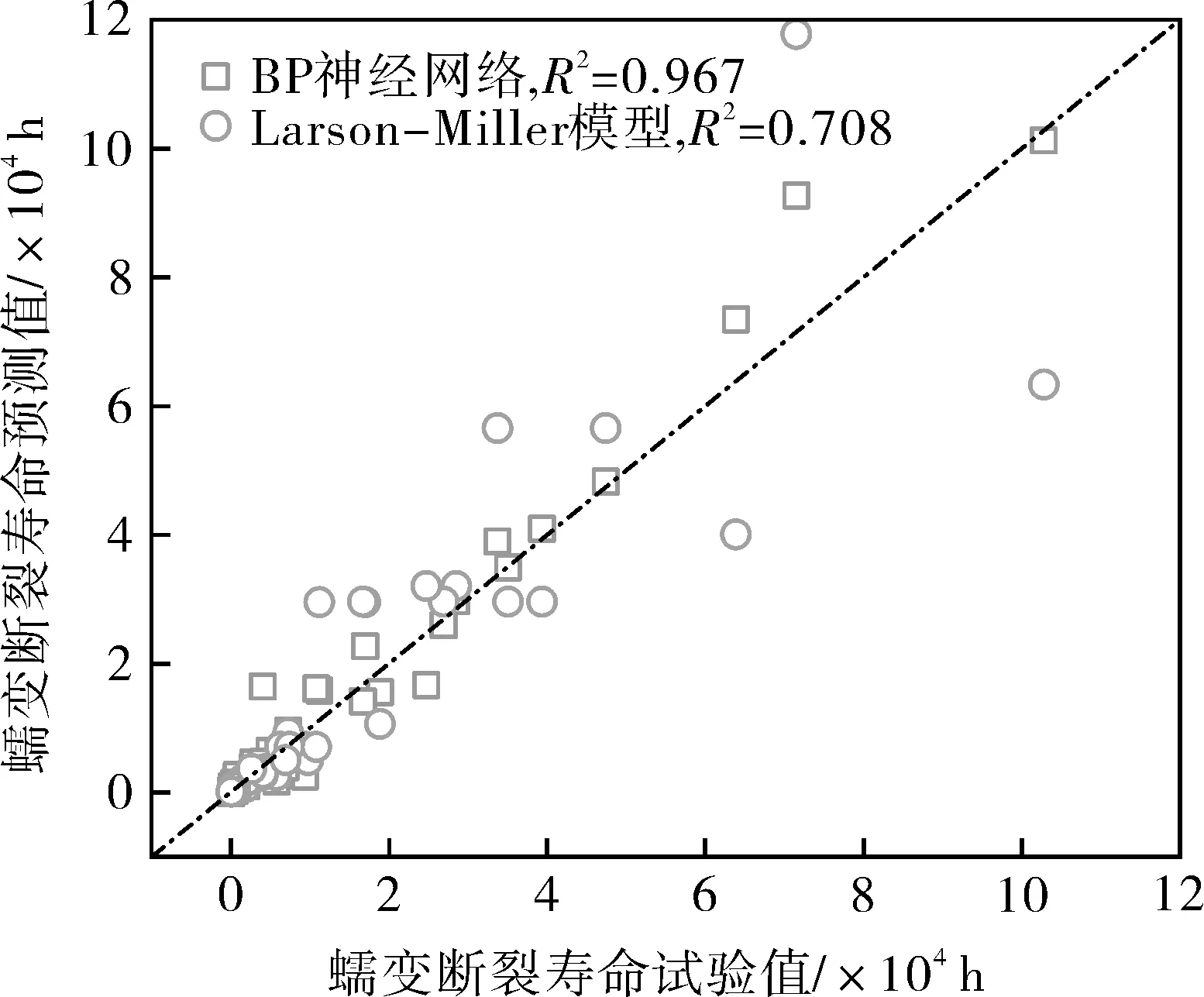
图11 BP神经网络及Larson-Miller模型蠕变断裂 寿命预测

4.3 支持向量机

使用文献[28]中开发的支持向量机工具箱LIBSVM对蠕变断裂寿命进行回归分析。选用两类回归支持向量机模型进行寿命预测，分别为e-SVM和v-SVM，前者训练速度较快，后者训练速度较慢，两者均选用高斯核函数。支持向量机模型存在多个超参数，其值将显著影响模型的预测效果。对于以上两类模型，均存在超参数C′和γ，使用网格搜索调参的方法确定两参数的最优值。另外，e-SVM需要优化参数p′，v-SVM需要优化参数n′，通过比较参数取不同值时的测试集决定系数确定最优参数值。

由图12可以看出，e-SVM与v-SVM具有相似的预测精度。当数据集含18种属性时，SVM模型预测精度低于2种属性及4种属性的预测精度，这说明SVM对多属性数据的学习能力受限。将主成分分析结果与SVM结合，可以将预测精度由0.854提高到0.955，显著改善了SVM模型的预测精度。

图12 不同属性数目数据集下的支持向量机 预测精度

4.4 随机森林

随机森林实质上是多决策树的组合模型，通过调整决策数棵树对模型性能进行优化。图13示出不同属性数目数据集下的随机森林模型预测精度，随机森林模型在数据集属性为18时预测精度较差，其预测精度低于2类属性及4类属性数据集的预测精度。将随机森林模型与主成分分析方法相结合，可以将测试集决定系数由0.746提高到0.95，显著提高了随机森林模型的性能。

图13 不同属性数目数据集下的随机森林 预测精度

4.5 高斯过程回归

使用训练集数据建立了GPR模型，模型采用了零均值函数、各向同性平方指数(Isotropic squared exponential)协方差函数及高斯似然函数。由图14可以看出，对于具有不同属性数目的数据集，高斯过程回归可以得到相似的预测精度，其值均在0.92左右。但是，当属性数目为2时，其训练集预测精度远小于属性数目为4及18对应的训练集预测精度。这说明当属性数目越多，高斯过程回归模型捕捉输入与输出之间映射关系的能力越强，样本数目越多，由属性数目导致的预测精度差异会越明显。对于当前数据集，高斯过程回归模型预测结果的方差最大在8左右，相对于断裂寿命该值非常小，这说明数据集内噪声很小，预测结果的不确定性可以忽略。

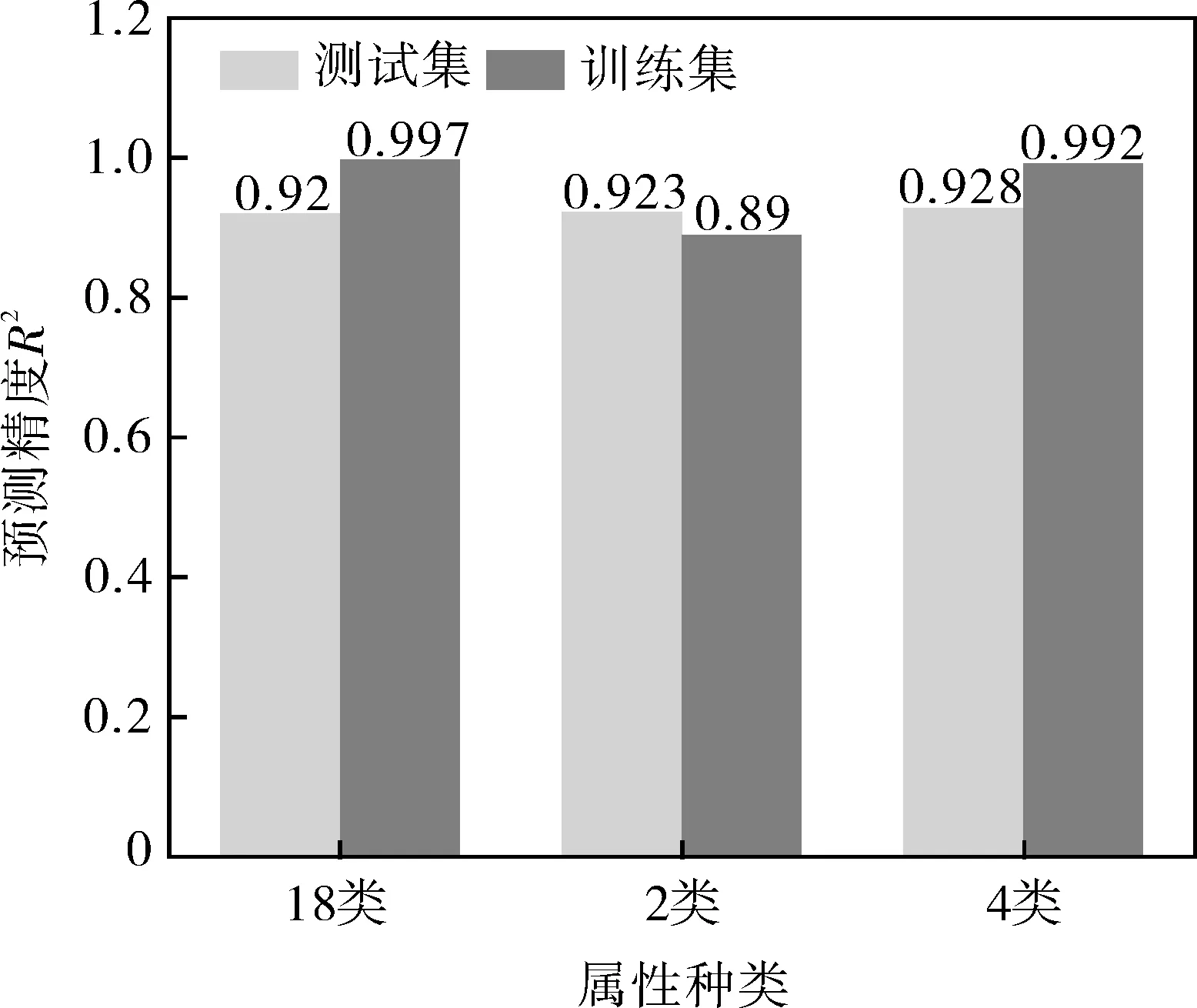
图14 不同属性数目数据集下的高斯过程回归预测精度

4.6 蠕变断裂性能影响因素分析

4.6.1 温度及应力的影响

当温度越高、应力越大时，蠕变损伤累积速率更快，进而导致蠕变断裂寿命越短。围绕这一特性，提出了许多半经验及经验蠕变断裂寿命预测方法。本部分基于前面使用18属性高维数据集建立的BP神经网络模型(隐含层单元数量为4)，研究温度及应力对蠕变断裂寿命的影响。图15,16分别示出神经网络模型预测的温度、应力与蠕变断裂寿命之间的关系。可以看出此模型能够捕捉到温度、应力与蠕变断裂寿命潜在的关系，即随着温度升高、应力增大，蠕变断裂寿命减小。

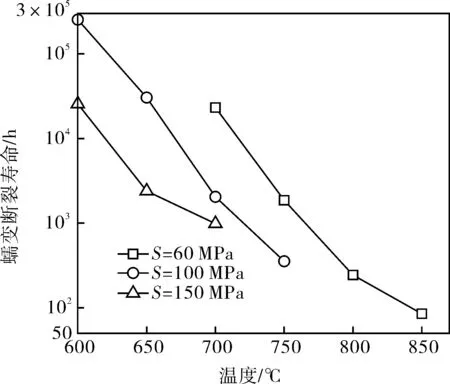
图15 不同温度下的316奥氏体不锈钢蠕变断裂寿命

图16 不同应力下 316奥氏体不锈钢蠕变断裂寿命

4.6.2 N含量的影响

当数据信息足够多时，即便是对于理论上难以建模的属性，也可以通过建立机器学习模型预测该属性对目标的影响。本部分基于18种属性数据集建立的BP神经网络模型，预测N元素含量对316奥氏体不锈钢蠕变断裂寿命的影响，数据集中N元素含量范围为0.015 9wt.%～0.035wt.%，预测范围为0.015wt.%～0.2wt.%。如图17所示，随着N含量的增加，蠕变断裂寿命显著增加，此趋势与文献[29]的结论是一致的。根据文献[29]的试验结果，N含量为0.22wt.%时，其蠕变断裂寿命是N含量为0.07wt.%对应蠕变断裂寿命的10倍，与机器学习模型的预测结果非常接近。N元素对蠕变断裂性能的改善作用与固溶强化过程中N元素的强化作用及碳氮化物的基体沉淀强化作用有关[29-31]。

4.7 结果讨论

本文基于高维数据集，使用BP神经网络、支持向量机、随机森林及高斯过程回归等机器学习方法对316奥氏体不锈钢的蠕变断裂寿命进行预测，发现基于机器学习的蠕变断裂寿命预测方法较之传统Larson-Miller方法具有更高的预测精度。并且机器学习模型可以预测不同属性对蠕变断裂性能的影响，为蠕变断裂性能的改善提供依据。

图17 N含量对蠕变断裂寿命的影响

总的来讲，神经网络模型预测精度最高，并且在高维数据集下预测精度显著高于低维数据下的预测精度。支持向量机及随机森林在多输入数据集的预测精度较低，将支持向量机、随机森林与主成分分析结合，可以显著提高两模型的预测精度；高斯过程回归在不同维度数据集下具有相似的预测精度，其预测精度低于前面三种模型。

基于前文的预测结果可以看出，机器学习中的黑箱模型(神经网络、支持向量机)捕捉数据潜在关系的能力会优于白箱模型(随机森林、高斯过程回归)。黑箱模型中，神经网络模型在高维数据集下的表达能力更强，预测精度更高，这说明这种分层的信号前向传播、误差反向传播结构适用于高维数据；以这种分层结构为基础演变而来的深度学习，在高维数据集、大数据集下具有非常强的表达能力[32-34]。

5 结论

机器学习可以克服解析解与经验解的局限性，为工程部件寿命预测提供可替代的解决方案。本研究提出了面向工程结构寿命预测问题的机器学习方案及优化的一般性方法，将机器学习方法用于316奥氏体不锈钢蠕变断裂寿命预测，可以得到比传统Larson-Miller方法更高的预测精度。其中BP神经网络在高维数据集下可以得到最高的预测精度，具有分层结构的神经网络在高维数据集下有更强的表达能力。基于建立的机器学习模型可以为材料性能改善提供参考。