大直径短桩的低应变检测

吴雨源

（惠东县建筑工程质量检测站，广东惠州 516300）

0 前言

在检测桩身完整性的方法中，低应变法因设备简便、检测快捷、费用低、结果较可靠等优点，成为检测机构中一种普查桩身质量的有力手段。目前，在广东省地基基础检测标准中，低应变法的理论基础是基于一维线弹性杆件模型这个假定，该假定要求受检桩的长径比、瞬态激励脉冲有效高频分量的波长与桩的横截面尺寸之比均不宜小于5[1]。但是，在工程检测中会经常遇到长径比小于5的大直径短桩，此类桩体的三维实体与一维波动理论之间的偏差导致对波速的影响，并随着长径比的不断减小，对波速的影响就越大。针对上述工程情况，低应变法是否仍然适用，且应如何获取准确的纵波波速以确定桩长和缺陷位置。

1 大直径短桩的三维效应

目前被工程检测人员广泛采用的低应变法是反射波法，是基于应力波在桩中的传播特性为理论基础的方法。在反射波法中，桩被视为一维弹性杆件，杆件的变形满足平截面假定，具体的说就是垂直于杆件轴线的各平截面（即杆的横截面）在杆件受拉伸、压缩或纯弯曲而变形后仍然为平面，并且同变形后的杆件轴线垂直，再通过相容方程、运动方程和材料的本构方程σ=σ（ε）推导出波动方程

现实中的桩为三维实体，锤击产生的应力波为三维应力波[2]，应力波不仅沿着桩身纵向传播，还沿着径向传播，随着长径比的不断减小，桩中质点横向运动的惯性作用越来越明显，这就是桩中应力波传播的三维效应现象。三维效应现象在大直径短桩的动测实践中具体表现在两个方面：①三维应力波在桩侧的反射效应使桩顶实测信号出现比较严重的高频干扰，从而增加桩顶实测信号的复杂性；②影响纵波波速继而造成实际缺陷位置和桩底位置的误判。

本质上讲，大直径短桩桩顶附近不可以完全套用一维应力波理论，取三维直角坐标系，则空间传播的应力波受式（1）控制[3]：

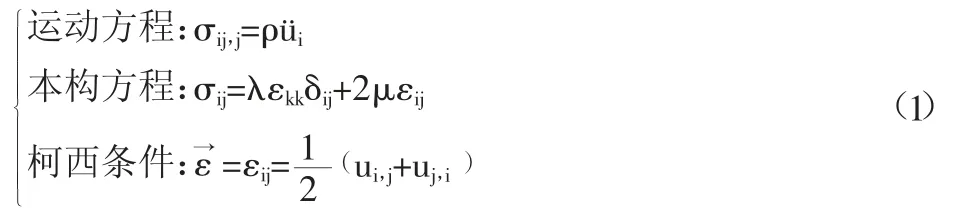
经过一系列换算和求解，得到三维状态下的纵波波速公式为：

式（2）建立起了三维纵波波速和一维理论纵波波速的关系。v为材料的泊松比，一般根式的数值是大于1的，即 CL＞Cb，这就是桩基动测实践中，为什么浅部缺陷实际开挖的深度往往比理论计算的深度深的原因，因为忽略了波速区别。

2 工程概况及实测数据

广东省惠东县某项目A因作为持力层的基岩埋藏浅，采用人工挖孔桩，直径为1.4m、1.6m和2.0m，长径比L/D在3.3～8.0区间内，混凝土设计强度强度为C45。整批桩采用低应变法普查桩身完整性。根据一维理论纵波波速公式取 E=3.45×104MPa，ρ=2400kg/m3，计算得到一维理论纵波波速为 3791m/s，而根据低应变法桩底反射时间可以确定纵波波速在3800～3900m/s，与理论公式计算的偏差约在2.8%以内。结合钻芯法的取样结果，将纵波波速的范围修正为3800～4050m/s之间，这个对应实际的三维纵波波速，它与一维理论波速的最大偏差约在6.8%，偏差较大。由此可以看出，一维波动理论只是一种近似假定，计算出来的纵波波速并不是一成不变的，它将随许多因素的变化而改变。

其中，项目A的某桩如图1所示。桩长为6.68m，桩径为2m，L/D=3.34，低应变法实测信号见图2。可知波速为4050m/s，如果按照一维理论纵波波速3791m/s去设置采样波速，其低应变信号见图3。桩长减少为6.25m，与实际桩长的偏差为6.9%。所以大直径短桩的纵波波速不能单纯地依靠一维理论纵波波速公式去设定，而是需要考虑桩的长径比，否则会因为大直径短桩的三维效应而低估了桩长或者浅判了桩身缺陷深度。

图1 项目A的大直径短桩

图2 项目A中某桩的低应变信号（波速为4050m/s）

图3 项目A中某桩的低应变信号（波速为3791m/s）

考虑到项目A工程桩的长径比在3.3～8.0之间，因此在低应变检测中使用了质地较硬的手锤，锤击时产生高频入射波有利于判别桩底以及桩身变化的反射信息。大直径短桩的几何尺寸不仅造成弥散现象，而且在桩顶附近传播的应力波属于三维球面波，这就要求回到三维状态去分析对波速的影响。

此外，选取广东省惠东县某项目B进行参照，该项目灌注桩桩径为1.2m，长径比在12～15之间，混凝土设计强度强度为C35，根据一维理论纵波波速公式取 E=3.35×104MPa，ρ=2400kg/m3，计算得到一维纵波波速为3736m/s。结合钻芯的桩长数据，该批桩的平均纵波波速为3795m/s。

3 大直径短桩的长径比对纵波波速的影响

从项目A和项目B中选取三种不同区间的长径比的波速数据，分别与一维理论纵波波速以及王雪峰[3]三维理论纵波波速Cb=1.054Cb进行比较，见表1。

通过表1可知，当长径比L/D小于5时，实际纵波波速与一维理论纵波波速的偏差在6%以上，与三维理论纵波波速的偏差约为1%，说明该区间的大直径短桩的三维效应非常明显，检测时若将波速设置为一维理论纵波波速，必然会造成桩底和缺陷深度的浅判，此时采用王雪峰推荐的三维理论纵波波速计算公式会更加合适。当长径比L/D介于5～10之间时，由于振源是频率较高的硬质锤，即使长径比L/D符合行业规范中受检桩长径比宜大于5的规定，实际纵波波速仍然比一维理论纵波波速大，偏差在4%左右，与三维理论纵波波速的偏差约为1.3%，此时采用王雪峰推荐的三维理论纵波波速计算公式也还是可以的。当长径比L/D大于10时，实际纵波波速与一维理论纵波波速的偏差在1.6%左右，与三维理论纵波波速的偏差在3.5%左右，此时采用一维理论纵波波速计算公式更加合适。

表1 纵波波速比较

4 结语

通过对项目A和项目B的实际纵波波速来看，低应变法在大直径短桩的桩身完整性检测中依然是可行的。在思想上不必受限于长径比宜大于5的规范要求。结合笔者的经验，在大直径短桩检测中要着重采用质地较硬的高频锤，通过变化锤击位置得到对大直径短桩桩身完整性的全面判断。根据三维应力波传播特征，利用纵波波速对不同长径比的三维效应的响应，实际检测中首先选取长径比大于10的灌注桩以确定整批桩的一维平均纵波波速，长径比越大，所获得的一维平均纵波波速就越接近一维理论纵波波速。当检测长径比介于5～10的灌注桩时，可以通过将一维平均纵波波速提高4%作为实际纵波波速用于精确计算，也可以采用王雪峰推荐的三维理论纵波波速作为实际纵波波速。当检测长径比小于5的灌注桩时，可以通过将一维平均纵波波速提高6%～7%作为实际纵波波速用于精确计算，长径比越小提高的越多，以避免对桩长的误判，导致获得一个假桩底。此外，对大直径短桩浅部缺陷位置的判断同样需要利用三维应力波传播特征，以避免缺陷位置被浅判。